1 今日打卡题
修剪二叉搜索树 669. 修剪二叉搜索树 - 力扣(LeetCode)
将有序数组转换为二叉树 108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
把二叉搜索树转换为累加树 538. 把二叉搜索树转换为累加树 - 力扣(LeetCode)
2 修剪二叉搜索树
2.1 思路
如果当前节点值大于 high,说明当前节点及其右子树都不符合条件,只需递归处理左子树并返回;
如果当前节点值小于 low,说明当前节点及其左子树都不符合条件,只需递归处理右子树并返回;
如果当前节点值在 [low, high] 范围内,则保留该节点,递归修剪其左、右子树后拼接到当前节点上,最后返回当前节点;
递归终止条件:遇到空节点时直接返回 null。
核心逻辑:利用 BST 的特性减少无效递归(节点值超限时,直接跳过一侧子树),递归修剪符合条件的节点;
递归终止:遇到空节点返回 null;
节点保留规则:值在 [low, high] 范围内时,保留节点并递归修剪其左右子树;值超限则返回另一侧子树的修剪结果。
2.2 实现代码
java
class Solution {
/**
* 修剪二叉搜索树,只保留值在 [low, high] 范围内的节点
* @param root 二叉搜索树的根节点
* @param low 下限值
* @param high 上限值
* @return 修剪后的二叉搜索树根节点
*/
public TreeNode trimBST(TreeNode root, int low, int high) {
// 递归终止条件:当前节点为空,直接返回null
if(root == null) return null;
// 情况1:当前节点值大于high,根据BST特性,其右子树所有节点都大于high,无需处理
// 只需递归修剪左子树,并返回左子树修剪后的结果
if(root.val > high) {
TreeNode left = trimBST(root.left, low, high);
return left;
}
// 情况2:当前节点值小于low,根据BST特性,其左子树所有节点都小于low,无需处理
// 只需递归修剪右子树,并返回右子树修剪后的结果
if(root.val < low) {
TreeNode right = trimBST(root.right, low, high);
return right;
}
// 情况3:当前节点值在[low, high]范围内,保留该节点
// 递归修剪左子树,将修剪后的左子树赋值给当前节点的左孩子
root.left = trimBST(root.left, low, high);
// 递归修剪右子树,将修剪后的右子树赋值给当前节点的右孩子
root.right = trimBST(root.right, low, high);
// 返回保留的当前节点(已完成左右子树的修剪)
return root;
}
}模拟:
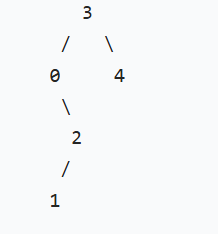
修剪范围:low=1,high=3(只保留值为 1、2、3 的节点)。
执行步骤:
调用 trimBST(3, 1, 3):
3 在 [1,3] 范围内,先处理左子树(节点 0),再处理右子树(节点 4)。
处理左子树:调用 trimBST(0, 1, 3):
0 < 1,需要递归处理其右子树(节点 2),返回右子树的修剪结果。
调用 trimBST(2, 1, 3):
2 在 [1,3] 范围内,处理左子树(节点 1),右子树为空(返回 null)。
调用 trimBST(1, 1, 3):
1 在 [1,3] 范围内,左右子树都为空,返回节点 1。
回到节点 2 的处理:
节点 2 的左孩子赋值为节点 1,右孩子为 null,返回节点 2。
回到节点 0 的处理:
节点 0 < 1,返回节点 2(其右子树的修剪结果),因此节点 3 的左孩子变为节点 2。
处理节点 3 的右子树:调用 trimBST(4, 1, 3):
4 > 3,递归处理其左子树(为空),返回 null,因此节点 3 的右孩子为 null。
最终返回节点 3,修剪后的树结构:

3 将有序数组转换为二叉树
3.1 思路
递归终止条件:当左指针 > 右指针时,说明当前子树无节点,返回 null;
确定根节点:取数组中间位置 mid 的元素作为当前子树的根节点;
构建左子树:递归处理数组左半部分 [left, mid-1],作为根节点的左子树;
构建右子树:递归处理数组右半部分 [mid+1, right],作为根节点的右子树;
返回当前根节点:完成当前子树的构建并返回。
3.2 实现代码
java
class Solution {
// 主方法:将有序数组转换为平衡二叉搜索树
public TreeNode sortedArrayToBST(int[] nums) {
// 调用递归构建方法,初始范围是整个数组(左边界0,右边界nums.length-1)
TreeNode root = build(nums, 0, nums.length - 1);
return root;
}
// 递归构建方法:参数为数组、当前子树对应的数组左边界、右边界
public TreeNode build(int[] nums, int left, int right) {
// 递归终止条件:左边界超过右边界,说明当前子树无节点,返回null
if (left > right) {
return null;
}
// 1. 找中间位置作为根节点(保证左右子树节点数尽可能相等,平衡)
int mid = (left + right) / 2;
// 2. 创建当前子树的根节点(值为中间位置的元素)
TreeNode root = new TreeNode(nums[mid]);
// 3. 递归构建左子树:范围是[left, mid-1],挂到当前根节点的左孩子
root.left = build(nums, left, mid - 1);
// 4. 递归构建右子树:范围是[mid+1, right],挂到当前根节点的右孩子
root.right = build(nums, mid + 1, right);
// 返回当前构建好的子树根节点
return root;
}
}4 把二叉搜索树转换为累加树
4.1 思路
要实现累加,关键是逆中序遍历 (右→根→左):
先遍历右子树(值更大的节点),再处理当前节点,最后遍历左子树;
用一个全局 / 引用变量记录 "累加和",遍历到当前节点时,将累加和赋值给当前节点,再把当前节点原值加到累加和中;
递归终止条件:遇到空节点直接返回。
4.2 实现代码
java
class Solution {
// 全局变量:记录累加和(初始为0)
private int sum = 0;
public TreeNode convertBST(TreeNode root) {
// 递归入口:逆中序遍历整棵树
traversal(root);
return root;
}
// 逆中序遍历函数(右→根→左)
private void traversal(TreeNode node) {
// 递归终止:节点为空,直接返回
if (node == null) {
return;
}
// 1. 先遍历右子树(值更大的节点)
traversal(node.right);
// 2. 处理当前节点:累加和赋值给当前节点,再更新累加和
sum += node.val; // 累加和 = 原有累加和 + 当前节点原值
node.val = sum; // 当前节点新值 = 累加和
// 3. 再遍历左子树(值更小的节点)
traversal(node.left);
}
}