FA_规划和控制(PC)-动态窗口(DWA)

田里的水稻2026-02-17 10:48

FA ：formulas and algorithm，PC ：planning and control，DWA：Dynamic Window Approach

DWA（动态窗口法）是移动机器人局部路径规划的经典算法，核心思想是在速度空间（线速度 v、角速度 ω）中采样多组控制量，预测每组控制量对应的短期轨迹，通过评价函数选择最优轨迹对应的控制量，实现实时避障和目标跟踪。

一、算法核心原理

1. 核心思想

DWA 不直接规划几何路径，而是在机器人当前可达的速度空间内采样控制量，通过「预测 - 评价 - 选择」的循环，实时输出最优的线速度和角速度，核心特点：

复制代码 
局部性：仅预测短期（通常 1~3 秒）轨迹，适合动态环境；
实时性：速度空间采样维度低（仅 v,ω），计算效率高；
安全性：综合考虑机器人动力学约束和障碍物碰撞约束。

2. 关键约束（动态窗口的定义）

DWA 的「动态窗口」是满足以下三类约束的速度集合 Vdw=(v,ω)V_{dw}={(v,ω)}Vdw=(v,ω)：

表格

约束类型 物理意义 数学表达
速度边界约束 机器人硬件限制的最大 / 最小速度 v∈[vmin,vmax],ω∈[ωmin,ωmax]v∈[v_{min},v_{max}],ω∈[ω_{min},ω_{max}]v∈[vmin,vmax],ω∈[ωmin,ωmax]
加速度约束 机器人在采样时间 Δt 内可达的速度范围（动力学限制） v∈[vcurr−av⋅Δt,vcurr+av⋅Δt]v∈[v_{curr}−a_v⋅Δt,v_{curr}+a_v⋅Δt]v∈[vcurr−av⋅Δt,vcurr+av⋅Δt]
障碍物约束 避免碰撞的最大安全速度（若以速度 v 运动，需保证能在碰撞前停下） v≤2⋅dmin⋅av,ω≤2⋅dmin⋅aωv≤\sqrt{2⋅d_{min}⋅a_v},ω≤\sqrt{2⋅d_{min}⋅a_ω}v≤2⋅dmin⋅av ,ω≤2⋅dmin⋅aω

dmin​ 是机器人到最近障碍物的距离

动态窗口是以上三类约束的交集，仅在该窗口内采样控制量，保证物理可达性和安全性。

3. 轨迹评价函数

对窗口内每个采样的 (v,ω)，预测其在时间 T 内的轨迹，通过以下加权评价函数打分，分数越高轨迹越优：

G(v,ω)=α⋅heading+β⋅dist+γ⋅velG(v,ω)=α⋅heading+β⋅dist+γ⋅velG(v,ω)=α⋅heading+β⋅dist+γ⋅vel

  • heading（方位角评价）heading（方位角评价）heading（方位角评价）：轨迹终点朝向目标点的程度（角度误差越小，分数越高）；
  • dist（距离评价）dist（距离评价）dist（距离评价）：轨迹与障碍物的最小距离（距离越大，分数越高，避免碰撞）；
  • vel（速度评价）vel（速度评价）vel（速度评价）：轨迹终点的线速度（速度越大，分数越高，提升运动效率）；
  • α,β,γα,β,γα,β,γ：权重系数，根据场景调整（如避障优先则增大 β）。

二、算法实现步骤（完整流程）

DWA 是「闭环迭代」算法，每一步的执行流程如下：

步骤拆解：

1. 状态感知

获取机器人当前状态：state=[x,y,θ,v,ω]state=[x,y,θ,v,ω]state=[x,y,θ,v,ω]（位置、航向角、当前线速度 / 角速度），以及目标点坐标、障碍物坐标。

2. 动态窗口计算

结合速度边界、加速度、障碍物约束，计算可行的速度范围 [vlow,vhigh][v_{low},v_{high}][vlow,vhigh] 和 [ω_{low​},ω_{high}​]。

3. 速度采样

在动态窗口内按采样分辨率（如 vsample=0.01m/s,ωsample=0.1rad/sv_{sample}=0.01m/s,ω_{sample}=0.1rad/svsample=0.01m/s,ωsample=0.1rad/s）遍历所有 (v,ω)(v,ω)(v,ω) 组合。

4. 轨迹预测

基于机器人运动学模型，预测每个采样控制量在 T 时间内的轨迹：两轮差速机器人运动学模型（核心）：
{xt+1=xt+v⋅cos(θt)⋅Δtyt+1=yt+v⋅sin(θt)⋅Δtθt+1=θt+ω⋅Δtvt+1=vωt+1=ω\begin{cases}x_{t+1}=x_t+v⋅cos(θt)⋅Δt \\ y_{t+1}=y_t+v⋅sin(θt)⋅Δt \\ θ_{t+1}=θ_t+ω⋅Δt \\ v_{t+1}=v \\ ω_{t+1}=ω\end{cases}⎩ ⎨ ⎧xt+1=xt+v⋅cos(θt)⋅Δtyt+1=yt+v⋅sin(θt)⋅Δtθt+1=θt+ω⋅Δtvt+1=vωt+1=ω

其中 Δt 是离散时间步长（通常 0.1s），循环预测直到时间达到 TTT（如 3s），得到轨迹点序列。

5. 轨迹评价

对每条预测轨迹计算三项评价指标：

  • 方位角评价：heading=π−∣θgoal−θtraj_end∣（θgoal 是轨迹终点到目标点的期望航向）；
  • 距离评价：dist=min(dtraj_point,obstacle)（轨迹所有点到最近障碍物的距离，若大于安全阈值则设为常数）；
  • 速度评价：vel=vtraj_end（轨迹终点的线速度）。

6. 最优控制量选择

选择评价分数最高的轨迹对应的 (v,ωv,ωv,ω)，作为机器人下一步的控制量。

7. 循环执行

机器人执行该控制量，更新状态后，重复上述步骤，直到到达目标点（与目标点距离≤机器人半径）。

三、DWA 的应用场景

DWA 是局部规划算法，适合动态、未知环境下的实时避障，典型应用：

  • 移动机器人避障：仓储 AGV、服务机器人、扫地机器人的实时路径调整；
  • 自动驾驶：低速场景（如园区无人车）的局部避障（常与全局规划算法如 A*、RRT * 结合）；
  • 无人机低空避障：无人机在复杂环境中的实时轨迹规划（需适配无人机运动学模型）；
  • 机械臂轨迹规划：关节空间的实时避障（修改速度空间为关节速度即可）。

优势与局限性

优势 局限性
计算效率高，实时性好 仅局部最优，可能陷入局部最小值（如 U 型障碍）
考虑机器人动力学约束 依赖准确的障碍物感知（激光雷达 / 视觉）
适配动态环境（障碍物移动） 对评价函数权重敏感，需调参适配场景

四、DWA 代码实现（核心模块解析）

以下基于之前修复的代码，拆解核心模块的实现逻辑：

python代码示例1：

1. 参数配置类（Config）

定义机器人硬件参数、采样参数、评价权重、障碍物 / 目标点坐标：

bash 复制代码 
class Config:
    def __init__(self):
        # 速度边界
        self.v_max = 1.0  # 最大线速度 [m/s]
        self.v_min = -0.5  # 最小线速度（支持后退）
        self.w_max = 40.0 * math.pi / 180.0  # 最大角速度 [rad/s]
        self.w_min = -40.0 * math.pi / 180.0
        # 加速度约束
        self.a_vmax = 0.2  # 最大线加速度 [m/ss]
        self.a_wmax = 40.0 * math.pi / 180.0  # 最大角加速度
        # 采样分辨率
        self.v_sample = 0.01  # 线速度采样步长
        self.w_sample = 0.1 * math.pi / 180.0  # 角速度采样步长
        # 预测时间与时间步长
        self.predict_time = 3.0  # 轨迹预测时长 [s]
        self.dt = 0.1  # 离散时间步长 [s]
        # 评价函数权重
        self.alpha = 0.15  # 方位角权重
        self.beta = 1.0    # 距离权重（避障优先）
        self.gamma = 1.0   # 速度权重
        # 机器人与环境参数
        self.robot_radius = 1.0  # 机器人半径（碰撞检测）
        self.ob = np.array([[0,2],[4,2],...])  # 障碍物坐标
        self.target = np.array([10,10])  # 目标点

2. DWA 核心类（DWA）

封装动态窗口计算、轨迹预测、评价逻辑：

bash 复制代码 
class DWA:
    def __init__(self, config):
        # 初始化参数（省略，对应Config的参数）
        self.dt = config.dt
        self.v_max = config.v_max
        # ... 其他参数
    
    def cal_dynamic_window_vel(self, v_curr, w_curr, state, obstacle):
        """计算动态速度窗口（三类约束的交集）"""
        # 1. 速度边界约束
        Vm = [self.v_min, self.v_max, self.w_min, self.w_max]
        # 2. 加速度约束
        Vd = [
            v_curr - self.a_vmax*self.dt, v_curr + self.a_vmax*self.dt,
            w_curr - self.a_wmax*self.dt, w_curr + self.a_wmax*self.dt
        ]
        # 3. 障碍物约束
        dist = self._dist(np.array([state]), obstacle)  # 到最近障碍物的距离
        Va = [
            self.v_min, np.sqrt(2*dist*self.a_vmax) if dist>0 else 0,
            self.w_min, np.sqrt(2*dist*self.a_wmax) if dist>0 else 0
        ]
        # 取交集
        v_low = max(Vm[0], Vd[0], Va[0])
        v_high = min(Vm[1], Vd[1], Va[1])
        w_low = max(Vm[2], Vd[2], Va[2])
        w_high = min(Vm[3], Vd[3], Va[3])
        return [v_low, v_high, w_low, w_high]
    
    def trajectory_predict(self, state_init, v, w):
        """轨迹预测：基于运动学模型生成轨迹"""
        state = np.array(state_init, copy=True)
        trajectory = np.array([state])
        time = 0
        while time < self.predict_time:
            state = KinematicModel(state, [v, w], self.dt)  # 运动学模型
            trajectory = np.vstack((trajectory, state))
            time += self.dt
        return trajectory
    
    def trajectory_evaluation(self, state, goal, obstacle):
        """轨迹评价：选择最优控制量"""
        G_max = -float('inf')
        control_opt = [0, 0]
        # 计算动态窗口
        dynamic_window = self.cal_dynamic_window_vel(state[3], state[4], state, obstacle)
        # 速度采样
        v_range = np.arange(dynamic_window[0], dynamic_window[1], self.v_sample)
        w_range = np.arange(dynamic_window[2], dynamic_window[3], self.w_sample)
        # 遍历所有采样速度
        for v in v_range:
            for w in w_range:
                traj = self.trajectory_predict(state, v, w)
                # 计算评价分数
                heading = self.alpha * self.__heading(traj, goal)
                dist = self.beta * self.__dist(traj, obstacle)
                vel = self.gamma * self.__velocity(traj)
                G = heading + dist + vel
                # 更新最优解
                if G > G_max:
                    G_max = G
                    control_opt = [v, w]
                    traj_opt = traj
        return control_opt, traj_opt
    
    # 评价函数子模块（省略，对应heading/dist/vel计算）
    def __heading(self, traj, goal): ...
    def __dist(self, traj, obstacle): ...
    def __velocity(self, traj): ...

3. 运动学模型（核心函数）

bash 复制代码 
def KinematicModel(state, control, dt):
    """两轮差速机器人运动学模型"""
    new_state = np.array(state, copy=True)
    new_state[0] += control[0] * math.cos(new_state[2]) * dt  # x位移
    new_state[1] += control[0] * math.sin(new_state[2]) * dt  # y位移
    new_state[2] += control[1] * dt  # 航向角更新
    new_state[3] = control[0]  # 线速度更新
    new_state[4] = control[1]  # 角速度更新
    return new_state
  1. 主循环（算法执行）
bash 复制代码 
def main(config):
    # 初始化机器人状态 [x, y, θ, v, ω]
    robot_state = np.array([0.0, 0.0, math.pi/8, 0.0, 0.0])
    dwa = DWA(config)
    full_trajectory = np.array([robot_state])
    
    plt.ion()  # 实时绘图
    while True:
        # 1. DWA算法获取最优控制量
        control, pred_traj = dwa.dwa_control(robot_state, config.target, config.ob)
        # 2. 更新机器人状态
        robot_state = KinematicModel(robot_state, control, config.dt)
        # 3. 绘图（省略）
        # 4. 检查是否到达目标
        dist_to_goal = math.hypot(robot_state[0]-config.target[0], robot_state[1]-config.target[1])
        if dist_to_goal <= config.robot_radius:
            print("到达目标！")
            break
    plt.ioff()
    plt.show()

4、关键调参指南

DWA 的效果依赖参数调优，核心参数调整原则：

  1. 预测时间（predict_time）：
  • 太小：轨迹太短，避障不充分；
  • 太大：计算量增加，且对动态环境适应差；
  • 推荐值：1 3s1~3s1 3s。
  1. 评价函数权重：
  • 避障优先：增大 βββ（如设为 2.02.02.0）；
  • 快速到达：增大 γγγ（如设为 1.51.51.5）；
  • 精准朝向：增大 ααα（如设为 0.50.50.5）。
  1. 采样分辨率：
  • 分辨率越高，轨迹越优，但计算量越大；
  • 推荐：vsample=0.01m/s,ωsample=0.1°/sv_{sample}=0.01m/s,ω_{sample}=0.1°/svsample=0.01m/s,ωsample=0.1°/s（转弧度）。

python代码示例2

bash 复制代码 
import numpy as np
import matplotlib.pyplot as plt
import copy
import math
import matplotlib

# 仅配置字体，移除所有celluloid相关代码
plt.rcParams['font.sans-serif'] = ['DejaVu Sans', 'Arial', 'Helvetica']  # 纯英文字体，避免任何字体问题
plt.rcParams['axes.unicode_minus'] = False
matplotlib.rcParams['font.family'] = 'sans-serif'

class Config:
    """
    simulation parameter class
    """
    def __init__(self):
        # robot parameter
        self.v_max = 1.0  # [m/s] 线速度上限
        self.v_min = -0.5  # [m/s] 线速度下限
        self.w_max = 40.0 * math.pi / 180.0  # [rad/s] 角速度上限
        self.w_min = -40.0 * math.pi / 180.0  # [rad/s] 角速度下限
        self.a_vmax = 0.2  # [m/ss] 线加速度上限
        self.a_wmax = 40.0 * math.pi / 180.0  # [rad/ss] 角加速度上限
        self.v_sample = 0.01  # [m/s] 线速度采样分辨率
        self.w_sample = 0.1 * math.pi / 180.0  # [rad/s] 角速度采样分辨率
        self.dt = 0.1  # [s] 离散时间步长
        self.predict_time = 3.0  # [s] 轨迹预测时长
        # 轨迹评价系数
        self.alpha = 0.15  # 方位角权重
        self.beta = 1.0    # 距离障碍物权重
        self.gamma = 1.0   # 速度权重
        
        self.robot_radius = 1.0  # [m] 机器人半径（碰撞检测）
        self.judge_distance = 10 # 障碍物安全距离阈值

        # 障碍物位置
        self.ob = np.array([
                    [-1, -1],
                    [-1.0,7.5],
                    [0, 2],
                    [2.0, 4.0],
                    [3.0, 11.0],
                    [4.0, 2.0],
                    [4.9, 4.0],
                    [5.3, 7.0],
                    [5.7, 9.0],
                    [8.0, 9.0],
                    [8.0, 6.0],
                    [7.0, 9.0], 
                    [8.0, 10.0],
                    [8.0, 1.3],
                    [9.0, 11.0],
                    [12.0, 13.0],
                    [12.0, 7.0],    
                    [12.0, 12.0],
                    [12.0, 3.0],
                    [8.1, 14.1],
                    [15.0, 15.0],
                    [15.0, 18.0],
                    [15.0, 1.0],
                    [13.0, 13.0]
                    ])
        # 目标点位置
        self.target = np.array([10,10])

class DWA:
    def __init__(self,config) -> None:
        """初始化DWA算法参数"""
        self.dt=config.dt
        self.v_min=config.v_min
        self.w_min=config.w_min
        self.v_max=config.v_max
        self.w_max=config.w_max
        self.predict_time = config.predict_time
        self.a_vmax = config.a_vmax
        self.a_wmax = config.a_wmax
        self.v_sample = config.v_sample
        self.w_sample = config.w_sample
        self.alpha = config.alpha
        self.beta = config.beta
        self.gamma = config.gamma
        self.radius = config.robot_radius
        self.judge_distance = config.judge_distance

    def dwa_control(self,state,goal,obstacle):
        """DWA算法主入口：输入当前状态，输出最优控制量和预测轨迹"""
        control,trajectory = self.trajectory_evaluation(state,goal,obstacle)
        return control,trajectory

    def cal_dynamic_window_vel(self,v,w,state,obstacle):
        """计算动态速度窗口（综合速度、加速度、障碍物约束）"""
        Vm = self.__cal_vel_limit()       # 速度边界约束
        Vd = self.__cal_accel_limit(v,w)  # 加速度约束
        Va = self.__cal_obstacle_limit(state,obstacle)  # 障碍物约束
        # 取各约束的交集
        v_low = max([Vm[0],Vd[0],Va[0]])
        v_high = min([Vm[1],Vd[1],Va[1]])
        w_low = max([Vm[2], Vd[2],Va[2]])
        w_high = min([Vm[3], Vd[3],Va[3]])
        return [v_low,v_high,w_low,w_high]

    def __cal_vel_limit(self):
        """速度边界约束"""
        return [self.v_min,self.v_max,self.w_min,self.w_max]
    
    def __cal_accel_limit(self,v,w):
        """加速度约束：计算当前速度下，dt时间内可达的速度范围"""
        v_low = v - self.a_vmax * self.dt
        v_high = v + self.a_vmax * self.dt
        w_low = w - self.a_wmax * self.dt
        w_high = w + self.a_wmax * self.dt
        return [v_low, v_high, w_low, w_high]
    
    def __cal_obstacle_limit(self,state,obstacle):
        """障碍物约束：避免碰撞的最大速度"""
        dist = self._dist(np.array([state]), obstacle)
        v_high = np.sqrt(2 * dist * self.a_vmax) if dist > 0 else 0
        w_high = np.sqrt(2 * dist * self.a_wmax) if dist > 0 else 0
        return [self.v_min, v_high, self.w_min, w_high]

    def trajectory_predict(self,state_init, v,w):
        """基于当前状态和控制量，预测未来轨迹"""
        state = np.array(state_init, copy=True)
        trajectory = np.array([state])
        time = 0
        while time < self.predict_time:
            state = KinematicModel(state, [v,w], self.dt)
            trajectory = np.vstack((trajectory, state))
            time += self.dt
        return trajectory

    def trajectory_evaluation(self,state,goal,obstacle):
        """轨迹评价：遍历速度窗口，选择最优轨迹"""
        G_max = -float('inf')
        trajectory_opt = np.array([state])
        control_opt = [0.,0.]
        # 计算动态速度窗口
        dynamic_window = self.cal_dynamic_window_vel(state[3], state[4], state, obstacle)
        
        # 速度采样（增加边界检查）
        v_range = np.arange(dynamic_window[0], dynamic_window[1], self.v_sample)
        w_range = np.arange(dynamic_window[2], dynamic_window[3], self.w_sample)
        if len(v_range) == 0: v_range = [dynamic_window[0]]
        if len(w_range) == 0: w_range = [dynamic_window[2]]
        
        # 遍历所有采样速度，评价轨迹
        for v in v_range:
            for w in w_range:
                trajectory = self.trajectory_predict(state, v, w)
                # 计算评价指标
                heading = self.alpha * self.__heading(trajectory, goal)
                dist = self.beta * self.__dist(trajectory, obstacle)
                vel = self.gamma * self.__velocity(trajectory)
                total_score = heading + dist + vel
                
                # 更新最优轨迹
                if total_score > G_max:
                    G_max = total_score
                    trajectory_opt = trajectory
                    control_opt = [v, w]

        return control_opt, trajectory_opt

    def _dist(self,state,obstacle):
        """计算机器人到最近障碍物的距离"""
        if len(obstacle) == 0:
            return float('inf')
        dx = state[:, 0][:, None] - obstacle[:, 0][None, :]
        dy = state[:, 1][:, None] - obstacle[:, 1][None, :]
        return np.min(np.hypot(dx, dy))

    def __dist(self,trajectory,obstacle):
        """距离评价：轨迹与障碍物的最小距离"""
        if len(obstacle) == 0:
            return self.judge_distance
        dx = trajectory[:, 0][:, None] - obstacle[:, 0][None, :]
        dy = trajectory[:, 1][:, None] - obstacle[:, 1][None, :]
        min_r = np.min(np.hypot(dx, dy))
        return min_r if min_r < (self.radius + 0.2) else self.judge_distance

    def __heading(self,trajectory, goal):
        """方位角评价：轨迹终点朝向目标的程度"""
        dx = goal[0] - trajectory[-1, 0]
        dy = goal[1] - trajectory[-1, 1]
        error_angle = math.atan2(dy, dx)
        cost_angle = error_angle - trajectory[-1, 2]
        return math.pi - abs(cost_angle)

    def __velocity(self,trajectory):
        """速度评价：轨迹终点的线速度"""
        return trajectory[-1, 3]

def KinematicModel(state,control,dt):
    """两轮差速机器人运动学模型"""
    new_state = np.array(state, copy=True)
    new_state[0] += control[0] * math.cos(new_state[2]) * dt  # x方向位移
    new_state[1] += control[0] * math.sin(new_state[2]) * dt  # y方向位移
    new_state[2] += control[1] * dt  # 航向角更新
    new_state[3] = control[0]  # 线速度更新
    new_state[4] = control[1]  # 角速度更新
    return new_state

def plot_arrow(x, y, yaw, length=0.5, width=0.1):
    """绘制机器人朝向箭头"""
    plt.arrow(x, y, length * math.cos(yaw), length * math.sin(yaw),
              head_length=width, head_width=width, color='red')

def plot_robot(x, y, yaw, config):
    """绘制机器人（圆形+朝向）"""
    # 绘制机器人本体（圆形）
    circle = plt.Circle((x, y), config.robot_radius, color='blue', alpha=0.3)
    plt.gca().add_patch(circle)
    # 绘制朝向
    end_x = x + config.robot_radius * math.cos(yaw)
    end_y = y + config.robot_radius * math.sin(yaw)
    plt.plot([x, end_x], [y, end_y], 'k-')

def main(config):
    # 初始化机器人状态 [x, y, yaw, v, w]
    robot_state = np.array([0.0, 0.0, math.pi / 8.0, 0.0, 0.0])
    goal = config.target
    obstacles = config.ob
    # 初始化DWA算法
    dwa = DWA(config)
    # 保存机器人完整轨迹
    full_trajectory = np.array([robot_state])
    
    # 设置绘图
    plt.figure(figsize=(10, 8))
    plt.ion()  # 开启交互模式
    
    try:
        while True:
            # DWA算法获取最优控制量和预测轨迹
            control, pred_trajectory = dwa.dwa_control(robot_state, goal, obstacles)
            # 更新机器人状态
            robot_state = KinematicModel(robot_state, control, config.dt)
            # 保存轨迹
            full_trajectory = np.vstack((full_trajectory, robot_state))
            
            # 清空画布，重新绘制
            plt.cla()
            # 绘制预测轨迹
            plt.plot(pred_trajectory[:, 0], pred_trajectory[:, 1], 'g--', label='Predicted Trajectory')
            # 绘制已走轨迹
            plt.plot(full_trajectory[:, 0], full_trajectory[:, 1], 'r-', label='Full Trajectory')
            # 绘制障碍物
            plt.scatter(obstacles[:, 0], obstacles[:, 1], c='black', s=50, label='Obstacles')
            # 绘制目标点
            plt.scatter(goal[0], goal[1], c='green', s=100, marker='*', label='Goal')
            # 绘制机器人
            plot_robot(robot_state[0], robot_state[1], robot_state[2], config)
            plot_arrow(robot_state[0], robot_state[1], robot_state[2])
            
            # 绘图设置
            plt.axis('equal')
            plt.grid(True)
            plt.legend(loc='upper right')
            plt.title('DWA Dynamic Window Approach Path Planning')
            plt.xlabel('X (m)')
            plt.ylabel('Y (m)')
            plt.pause(0.01)
            
            # 检查是否到达目标
            dist_to_goal = math.hypot(robot_state[0] - goal[0], robot_state[1] - goal[1])
            if dist_to_goal <= config.robot_radius:
                print("Goal Reached! 到达目标点！")
                break
                
    except KeyboardInterrupt:
        print("\nProgram Interrupted by User! 程序被用户中断")
    finally:
        plt.ioff()  # 关闭交互模式

    # 绘制最终结果
    plt.cla()
    plt.plot(full_trajectory[:, 0], full_trajectory[:, 1], 'r-', linewidth=2, label='Final Trajectory')
    plt.scatter(obstacles[:, 0], obstacles[:, 1], c='black', s=50, label='Obstacles')
    plt.scatter(goal[0], goal[1], c='green', s=100, marker='*', label='Goal')
    plot_robot(robot_state[0], robot_state[1], robot_state[2], config)
    plt.axis('equal')
    plt.grid(True)
    plt.legend(loc='upper right')
    plt.title('DWA Path Planning - Final Result')
    plt.xlabel('X (m)')
    plt.ylabel('Y (m)')
    plt.show()

if __name__=="__main__":
    main(Config())

代码结果 ：

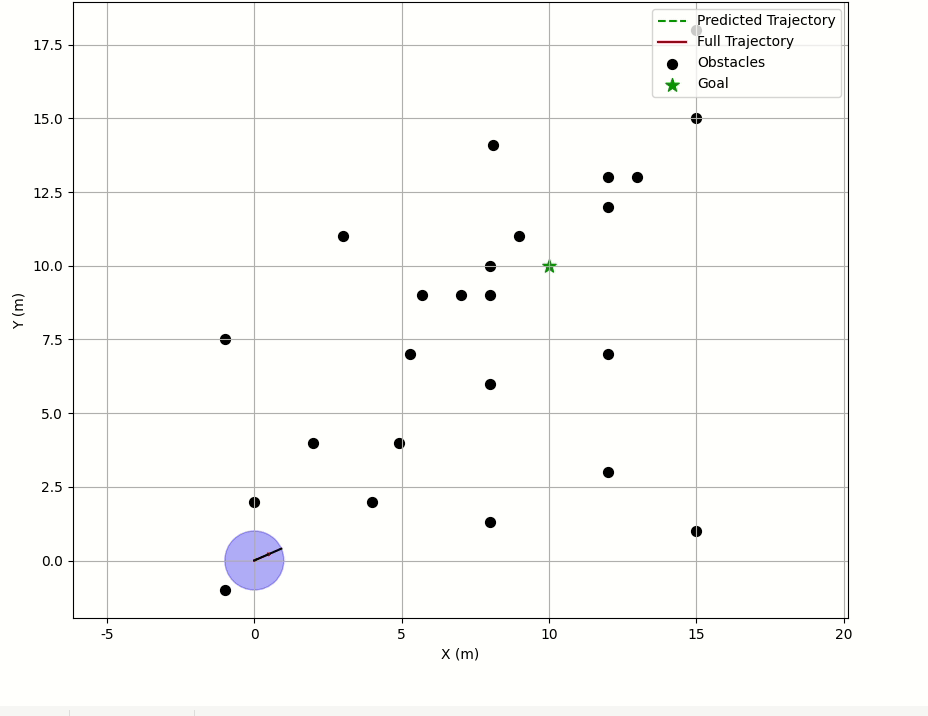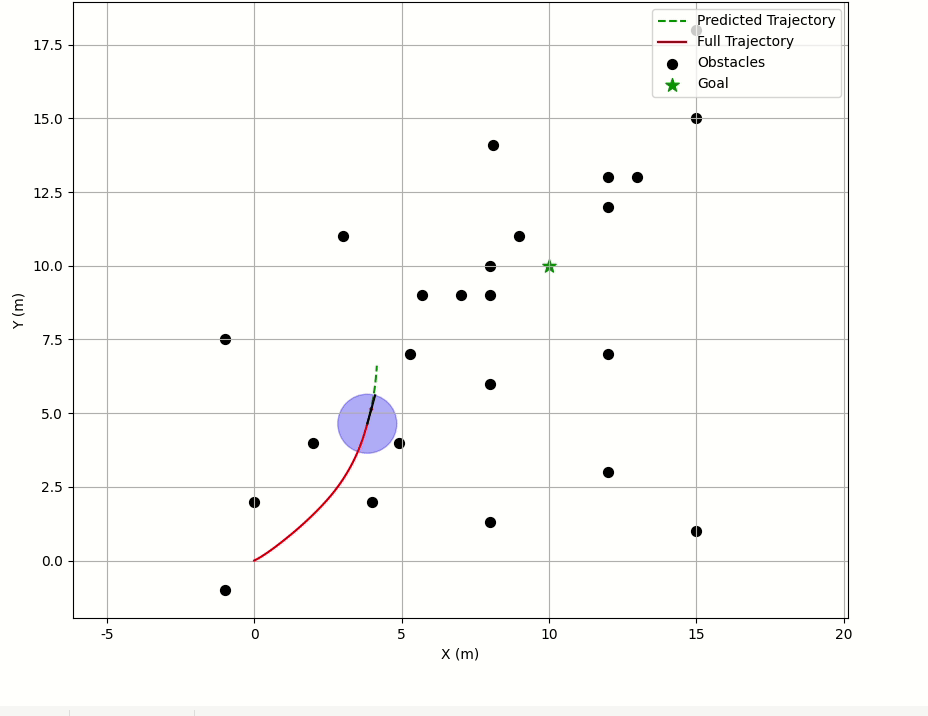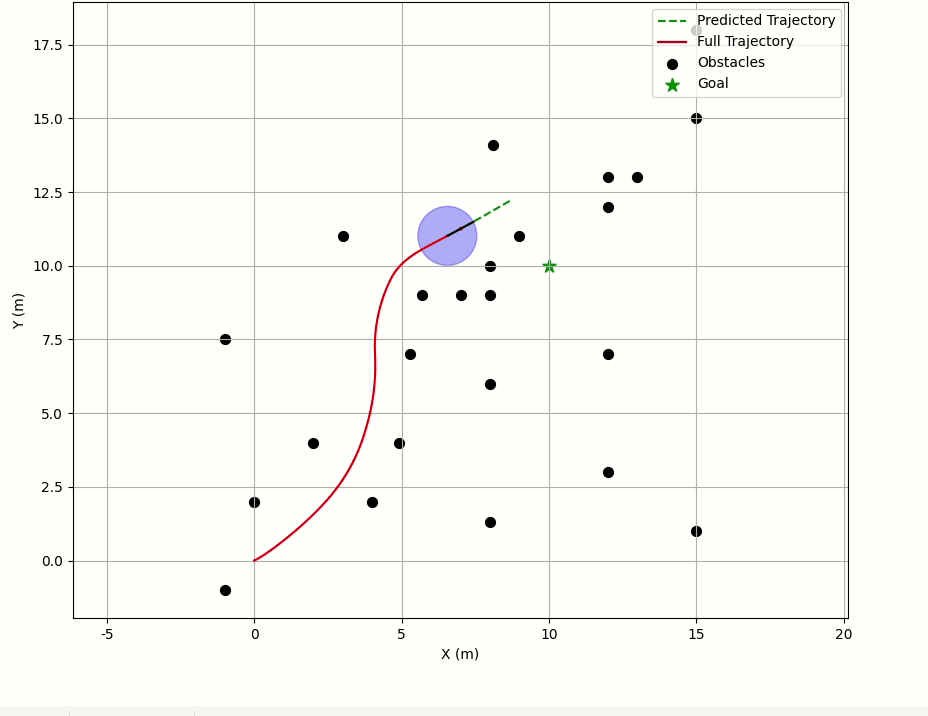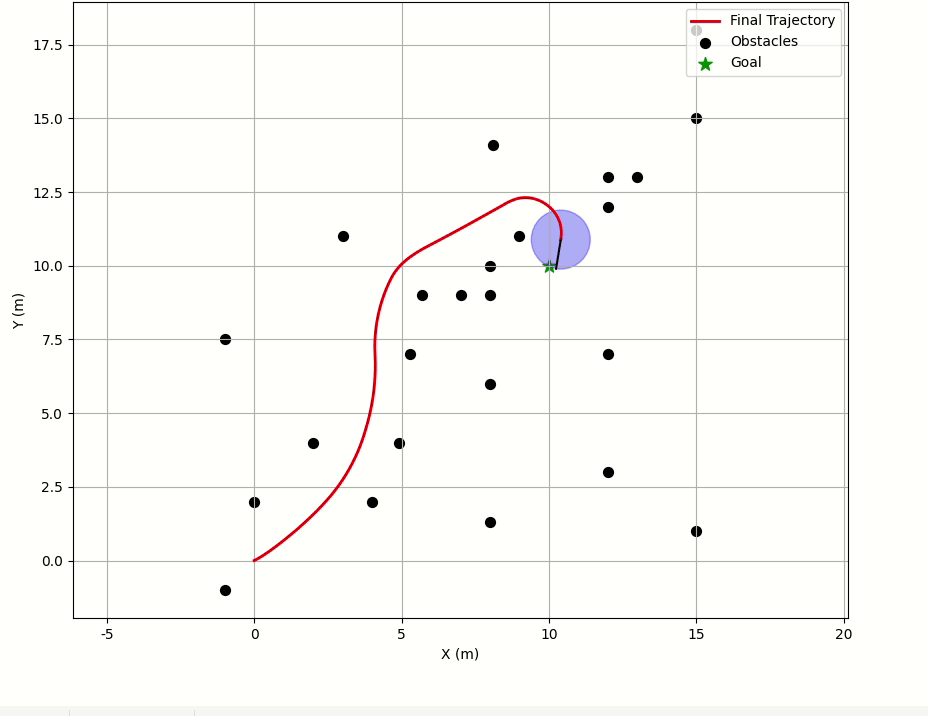
五、结束语

核心要点

  • DWA 是速度空间的局部规划算法，通过「约束采样 - 轨迹预测 - 评价选择」实现实时避障；
  • 动态窗口是算法的核心，保证控制量的物理可达性和安全性；
  • 评价函数是调优关键，需根据场景平衡「朝向、避障、速度」三大目标；
  • 适合动态环境，但需与全局规划算法结合（如 A*）避免局部最优。

代码核心

  • 运动学模型是轨迹预测的基础，需匹配机器人类型；
  • 动态窗口计算是约束的交集，缺一不可；
  • 评价函数的设计决定了算法的行为（避障 / 速度 / 朝向优先）。

DWA 是移动机器人局部规划的入门算法，理解其原理后，可扩展到多机器人、三维空间（无人机）等场景，仅需修改运动学模型和速度空间维度即可。

相关推荐
阿里云大数据AI技术10 分钟前
PAI Physical AI Notebook详解8：Isaac Lab Arena 全身机器人机动+操控工作流
人工智能
高木木的博客24 分钟前
数字架构智能化测试平台(1)--总纲
人工智能·python·nginx·架构
wanghowie26 分钟前
11. AI 客服系统架构设计：不是调 API，而是系统工程
人工智能·系统架构
袋鼠云数栈UED团队32 分钟前
基于 OpenSpec 实现规范驱动开发
前端·人工智能
Raink老师34 分钟前
【AI面试临阵磨枪】什么是 Tokenization？子词分词（Subword）的优缺点？
人工智能·ai 面试
迷你可可小生1 小时前
面经（三）
人工智能·rnn·lstm
逻辑驱动的ken1 小时前
Java高频面试考点场景题09
java·开发语言·数据库·算法·oracle·哈希算法·散列表
云烟成雨TD1 小时前
Spring AI Alibaba 1.x 系列【28】Nacos Skill 管理中心功能说明
java·人工智能·spring
AI医影跨模态组学1 小时前
Cancer Letters（IF=10.1）中科院自动化研究所田捷等团队：整合纵向MRI与活检全切片图像用于乳腺癌新辅助治疗反应的早期预测及个体化管理
人工智能·深度学习·论文·医学·医学影像
oioihoii1 小时前
Graphify 简明指南
人工智能
热门推荐
012026年4月技术前沿：AI大模型爆发、智能体革命与量子安全新纪元02GitHub 镜像站点032026 年 AI 编程助手全面对比评测：Cursor vs Copilot vs Claude Code vs GitHub Copilot Free042026年4月AI大事件深度解读：大模型竞争进入“深水区“05Claude Code Windows 兼容性问题：指定版本 2.1.112 可解决06AI Weekly | 2026年4月第二周 · GitHub热门项目与AI发展趋势深度解析07UBUNTU Claude Code 报错 claude native binary not installed08近期有什么ai的新消息，新动态？ 2026.4月09从限购到畅通：GLM-5.1 Coding Plan接入攻略10从零部署 Hermes Agent：一只"会成长的 AI 马"保姆级安装教程