hot 100 第二十九题 29.删除链表的倒数第 N 个结点

题目

给你一个链表，删除链表的倒数第 n个结点，并且返回链表的头结点。

示例 1：

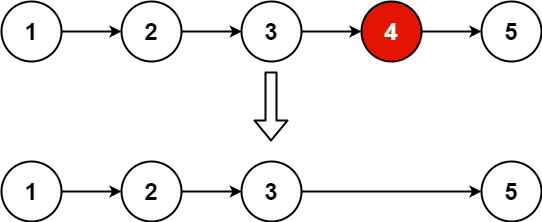
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

核心思路

双指针（快慢指针）：让快指针先走n步，然后快慢指针一起走，当快指针到达末尾时，慢指针正好在倒数第n+1个节点（待删除节点的前一个）。

链表: 1 → 2 → 3 → 4 → 5
删除倒数第2个节点（节点4）

快指针先走2步:
      fast
        ↓
1 → 2 → 3 → 4 → 5

然后一起走，fast到末尾时:
        slow     fast
          ↓        ↓
1 → 2 → 3 → 4 → 5 → null

slow.next = slow.next.next
结果: 1 → 2 → 3 → 5

🧩 核心原理：保持固定距离

双指针的关键在于：让快指针和慢指针之间始终保持 n 个节点的距离。

第一步：快指针先走 n 步

• 假设链表有 L 个节点（从 1 到 L 编号）。
• 初始时，快、慢指针都在头节点（位置 1）。
• 快指针先走 n 步 → 此时快指针在 第 (1 + n) 个节点（即位置 n+1）。
• 慢指针仍在位置 1。
• 两者之间的距离 = n 个节点（或者说，快指针比慢指针多走了 n 步）。

✅ 举例：n=2，快指针走到第 3 个节点，慢还在第 1 个，中间隔了 2 个节点（1→2→3），距离为 2。

---

第二步：快慢指针同步前进

• 每次都让快、慢各走 1 步。
• 因为它们速度相同 ，所以它们之间的距离始终保持为 n。

---

第三步：当快指针到达末尾（即 fast == null）

注意：通常我们说"快指针到达末尾"，是指它走到了最后一个节点的 next（即 null）。

• 链表有 L 个节点，最后一个节点是第 L 个。
• 当 fast == null 时，说明快指针已经走过了 L 个节点，现在在第 L+1 个位置（null）。
• 因为快指针比慢指针多走了 n 步，所以：
  • 慢指针此时走到了第 (L + 1) - n 个位置。
  • 即：慢指针在第 (L - n + 1) 个节点。

题解

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 使用哑节点简化边界处理
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        
        ListNode fast = dummy;
        ListNode slow = dummy;
        
        // 快指针先走 n+1 步
        for (int i = 0; i <= n; i++) {
            fast = fast.next;
        }
        
        // 快慢指针一起走，直到fast到达末尾
        while (fast != null) {
            fast = fast.next;
            slow = slow.next;
        }
        
        // 删除倒数第n个节点
        slow.next = slow.next.next;
        
        return dummy.next;
    }
}
```

## 详细演示
```
链表: 1 → 2 → 3 → 4 → 5
n = 2（删除倒数第2个，即节点4）

步骤1: 创建哑节点
------------------
dummy → 1 → 2 → 3 → 4 → 5

fast = dummy
slow = dummy

步骤2: fast 先走 n+1 步（3步）
------------------
i=0: fast = 1
i=1: fast = 2
i=2: fast = 3

现在:
dummy → 1 → 2 → 3 → 4 → 5
slow↑           fast↑

步骤3: 快慢指针一起走
------------------
第1次移动:
dummy → 1 → 2 → 3 → 4 → 5
        slow↑       fast↑

第2次移动:
dummy → 1 → 2 → 3 → 4 → 5 → null
            slow↑       fast↑

第3次移动:
dummy → 1 → 2 → 3 → 4 → 5 → null
                slow↑       fast↑

fast = null，循环结束

步骤4: 删除节点
------------------
slow 指向节点3（倒数第3个）
slow.next = 4（倒数第2个，待删除）
slow.next.next = 5（倒数第1个）

执行: slow.next = slow.next.next

dummy → 1 → 2 → 3 → 5
                ↓
               (4被跳过)

返回 dummy.next
结果: 1 → 2 → 3 → 5
```

## 为什么快指针要走 n+1 步？
```
目标: 让slow停在待删除节点的前一个

如果fast走n步:
链表: 1 → 2 → 3 → 4 → 5, n=2

fast走2步后:
dummy → 1 → 2 → 3 → 4 → 5
slow↑       fast↑

一起走，fast到null:
dummy → 1 → 2 → 3 → 4 → 5 → null
            slow↑       fast↑

slow指向节点2，但我们需要它指向节点3！

如果fast走n+1步:
fast走3步后:
dummy → 1 → 2 → 3 → 4 → 5
slow↑           fast↑

一起走，fast到null:
dummy → 1 → 2 → 3 → 4 → 5 → null
                slow↑       fast↑

slow指向节点3 ✓ 正确！
```

## 图解双指针间距
```
链表长度L，删除倒数第n个

fast先走n+1步，fast和slow间距为n+1:

dummy → ... → slow → n个节点 → fast → ... → null
        ↑                      ↑
     倒数第n+1个            当前位置

当fast到达null:
dummy → ... → slow → 待删除 → ... → null
              ↑
          倒数第n+1个

slow.next就是倒数第n个，要删除的节点
```

## 为什么需要哑节点？

### 场景：删除头节点
```
链表: 1 → 2 → 3
n = 3（删除倒数第3个，即头节点1）

没有哑节点:
fast走3步会越界！
而且删除头节点需要特殊处理

有哑节点:
dummy → 1 → 2 → 3

fast走4步:
dummy → 1 → 2 → 3 → null
slow↑               fast↑

一起走后:
dummy → 1 → 2 → 3 → null
slow↑       fast↑

slow.next = slow.next.next
dummy → 2 → 3 ✓

统一处理，无需特殊判断

本质

这道题体现了双指针的间距控制：

1. 固定间距 --- fast和slow保持n+1的距离
2. 同步移动 --- 一起移动直到fast到末尾
3. 精准定位 --- slow自然停在目标位置

配合哑节点技巧，使得代码简洁统一，不需要特殊判断。