再论自然数全加和 - 欧拉伽马常数

铸人2026-02-17 15:14

此处具体算一下欧拉伽马常数是怎么得到的。

在，

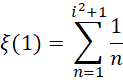
中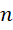，和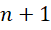之间的1个单位，被平分成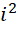份，如果周期是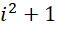，但这个平分的每一份都取边界值的倒数为结果。而在，

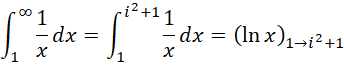
过程中，每一个单位也被平分成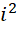份，周期也是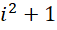，但是这平分的每一份则取对应数值的倒数为结果。所以，对于积分形式，

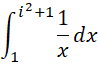
来说，整个区间被分成，

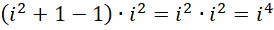
份，每一份的单位是。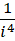

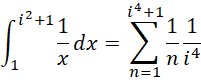
而对于求和形式，

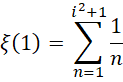
来说，整个区间被分成，

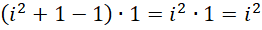
份，每一份的单位都是1。相比较而言，积分形式的对应的求和份数更多，细节更细，

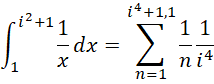
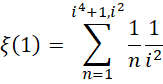
在每个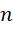到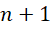的区间，积分形式为，

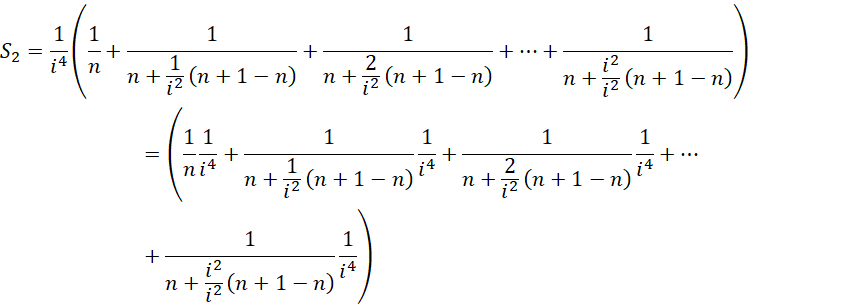
将内部精度提升到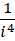

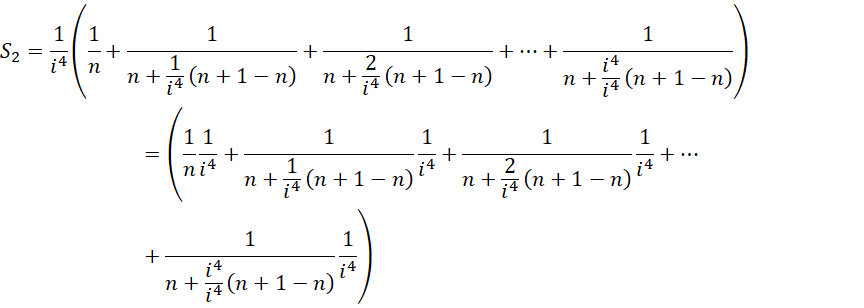
求和形式为，

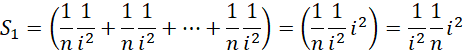
将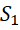的每个部分都提升精度到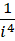

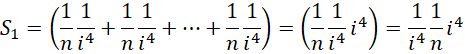
以最高精度计算面积的差值是，

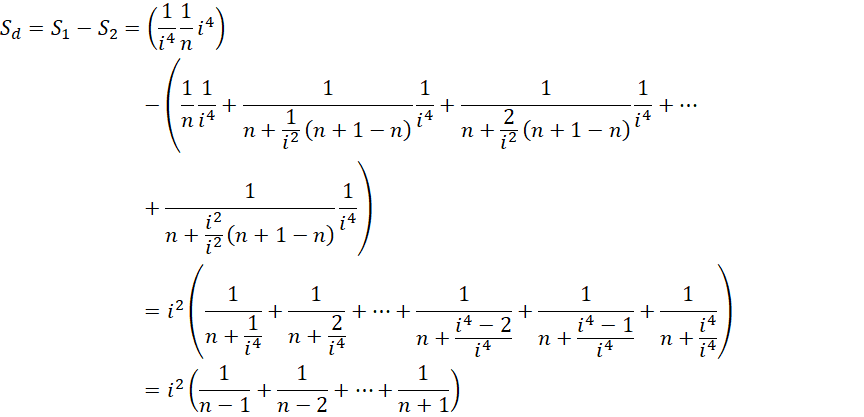
每一个微小面积，

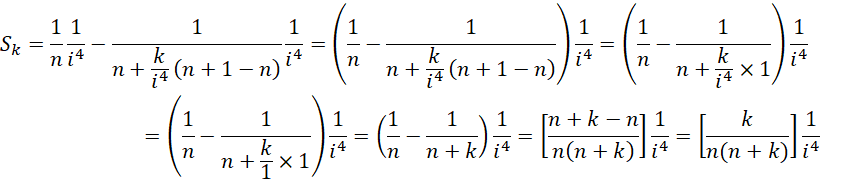
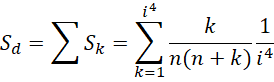
以最高精度计算的总面积差为，

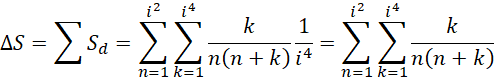
这里的内层分的更细，外层没有那么细。回到微小面积，

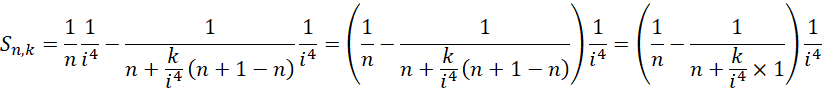
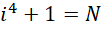
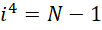
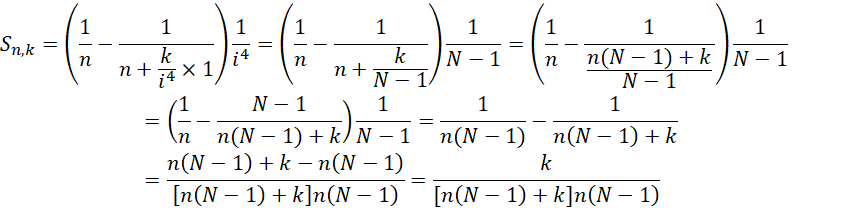
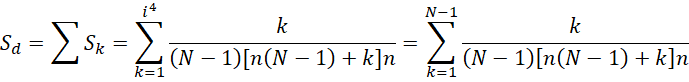
以最高精度计算的总面积差为，

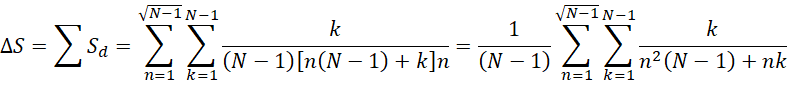
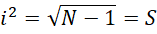
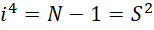
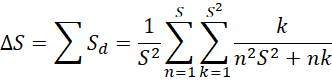
这个公式用程序验证，得到很好的结果。

cs 复制代码

    static double GetGamma(long S = 10000)
    {
        var q = S * S;
        var s = 0.0;
        for (var n = 1L; n <= S; n++)
        {
            for (var k = 1L; k <= q; k++)
            {
                s += k / (1.0 * n * n * q + 1.0 * n * k);
            }
        }
        return s / q;
}
r=0.5771647389914232
γ=0.5772156649015329
(γ-r)/γ=(0.5772156649015329-0.5771647389914232)/0.5772156649015329=8.82268×10^(-5)