题目
TUOJ
https://sim.csp.thusaac.com/contest/40/problem/2
思路参考：
第40次CSP认证前四题 - Oaths - 博客园https://www.cnblogs.com/oaths/articles/19327767
80分
经过尝试，如果只实现顺时针旋转90度的函数，转180调用2次，转270调用三次，只能得75分，会有5个测试点TLE
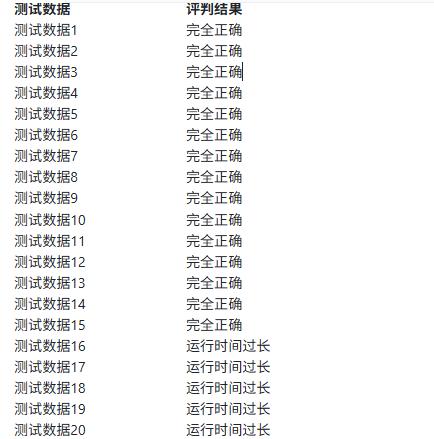
实际上实现如下旋转的函数后还是只能75分
在AI的建议下，使用memcpy和reverse进行一点常数优化之后可以得80分，对此，AI给出的解释是
标准库函数 memcpy 和 std::reverse 利用 SIMD（单指令多数据并行） 指令集（如 AVX/SSE）进行大块数据处理，其单周期处理能力和内存带宽利用率远高于逐字节操作的手写 for 循环。
（在知乎上有大佬说测试数据比较水，小常数可以过，不知道我这份代码哪里还能常数优化，希望有大佬不吝赐教）
可以让AI总结一下目前的代码逻辑：
程序整体功能
这是一个矩阵解密程序，输入一个经过加密的字符矩阵和一组密钥，通过逆向执行加密操作，还原出原始矩阵。
核心数据结构
a矩阵：大小为 405×405，存储当前字符矩阵（下标从1开始）
b矩阵：辅助矩阵，用于旋转操作时的临时存储
z：当前矩阵的边长主要操作类型
程序处理两种加密操作：
1. 翻转操作（op=2）
上下翻转：将指定矩形区域上下对称交换
左右翻转 ：将指定矩形区域左右对称交换（使用
reverse优化）2. 旋转操作（op=1）
支持顺时针旋转 90°、180°、270°
使用辅助矩阵
b暂存，再用memcpy批量复制回原矩阵（常数优化）包含全局旋转：会旋转整个矩阵（这是题目要求的）
执行流程
读取输入：矩阵大小 z、矩阵内容、密钥长度 k、密钥序列
逆向执行：从密钥序列末尾开始，每6个数字为一组操作，倒序执行
每组第一个数字是操作类型（1或2）
后面5个数字是操作参数（坐标、边长、角度等）
输出结果：找到左上角连续非 '?' 的区域，输出其大小和内容
关键特点
逆向解密：加密时顺序执行操作，解密时倒序执行
坐标系统：所有坐标从1开始计数
常数优化 ：使用
reverse和memcpy提高性能这个程序的核心思想是逆向操作，通过倒序执行加密操作的逆过程来还原原始矩阵。
cpp
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
const int Z=405;
char a[Z][Z]; //1~Z 1~Z
char b[Z][Z]; //辅助矩阵 ，从(1,1)开始 只存需要旋转的小矩阵
int z;
void print()
{
for(int i=1;i<=z;i++){
for(int j=1;j<=z;j++)
cout<<a[i][j];
cout<<endl;
}
}
int ui,di,li,ri,oi;
void decodeFan()
{
if(oi==1){ //上下
for(int i=1;i<=(di-ui+1)/2;i++) //warn:i<=(di-ui+1)/2
{
for(int j=li;j<=ri;j++)
{
swap(a[ui+i-1][j],a[di-(i-1)][j]);
}
}
}
else {//-1 左右
// for(int j=1;j<=(ri-li+1)/2;j++) //warn
// {
// for(int i=ui;i<=di;i++)
// {
// swap(a[i][li+j-1],a[i][ri-(j-1)]);
// }
// }
for (int i = ui; i <= di; i++) {
// 常数优化：使用内置 reverse
reverse(&a[i][li], &a[i][ri + 1]); //反转容器或数组中指定范围内的元素顺序。它的参数要求是一个左闭右开的区间
}
}
}
//顺时针旋转90度*t次
void Xuan(int x,int y,int l,int t) { //time 次数
if(t==0) return; //旋转0次
if(t==1) //顺时针转90度 转1次
for (int i = 1; i <= l; i++) {
for (int j = 1; j <= l; j++) {
b[j][l-i+1] = a[x+i-1][y+j-1];
}
}
else if(t==2){ //顺时针转180度 2次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-i+1][l-j+1] = a[x+i-1][y+j-1];
}
}
else if(t==3){//顺时针转270度 3次
for (int i = 1; i <= l; i++)
for (int j = 1; j <= l; j++) {
b[l-j+1][i] = a[x+i-1][y+j-1];
}
}
// //复制回去
// for(int i = 1; i <= l ; i ++ )
// for(int j = 1 ; j <= l; j ++ ){
// a[x + i - 1][y + j - 1] = b[i][j];
// }
//常数优化：使用 memcpy 进行整行拷贝
for (int i = 1; i <= l; i++) {
memcpy(&a[x + i - 1][y], &b[i][1], l*sizeof(char)); //memcpy(目标地址, 源地址, 字节数)
}
}
int vi; //旋转的参数 ui,vi,li,di,ri 另外四个复用一下
void decodeXuan()
{
//整体顺时针转ri次 90度
ri=ri%4;
if(ri!=0)
Xuan(1,1,z,ri); //旋转0次 即 不旋转
int ni_ri=(di/90)%4;//di∈{90,180,270},
Xuan(ui,vi,li,4-ni_ri); //逆时针转i次=顺时针转4-i次
}
void solve()
{
cin>>z;
for(int i=1;i<=z;i++)
{
string s; cin>>s;
for(int j=1;j<=z;j++)
a[i][j]=s[j-1];
}
// print();
int k; cin>>k;
int keys[k+5]={}; //密钥序列
for(int i=0;i<k;i++) cin>>keys[i];
for(int i=k-6;i>=1;i-=6) //ERROR:倒着读取才对
{
int op=keys[i];
if(op==2)
{
//翻转的参数 ui,di,li,ri,oi;
ui=keys[i+1],di=keys[i+2],
li=keys[i+3],ri=keys[i+4],oi=keys[i+5];
decodeFan(); //翻转
}
else {
//旋转的参数 ui,vi,li,di,ri
ui=keys[i+1],vi=keys[i+2],
li=keys[i+3],di=keys[i+4],ri=keys[i+5];
decodeXuan();
}
}
// print();
int n=0,m=0;
while(a[1][m+1]!='?'&&m+1<=z) m++;
while(a[n+1][1]!='?'&&n+1<=z) n++;
cout<<n<<" "<<m<<endl;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
cout<<a[i][j];
cout<<endl;
}
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0);
solve();
return 0;
}正解思路
【直播回放】第40次CCFCSP认证真题精讲 2025年12月10日19点场_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV16fmtBYEFj/?spm_id_from=333.1391.0.0&vd_source=5366be93f43e6a40161aecaec29f4a2a该讲解指出了正解：旋转局部矩阵和旋转矩阵整体，这两个操作的顺序是可以交换的
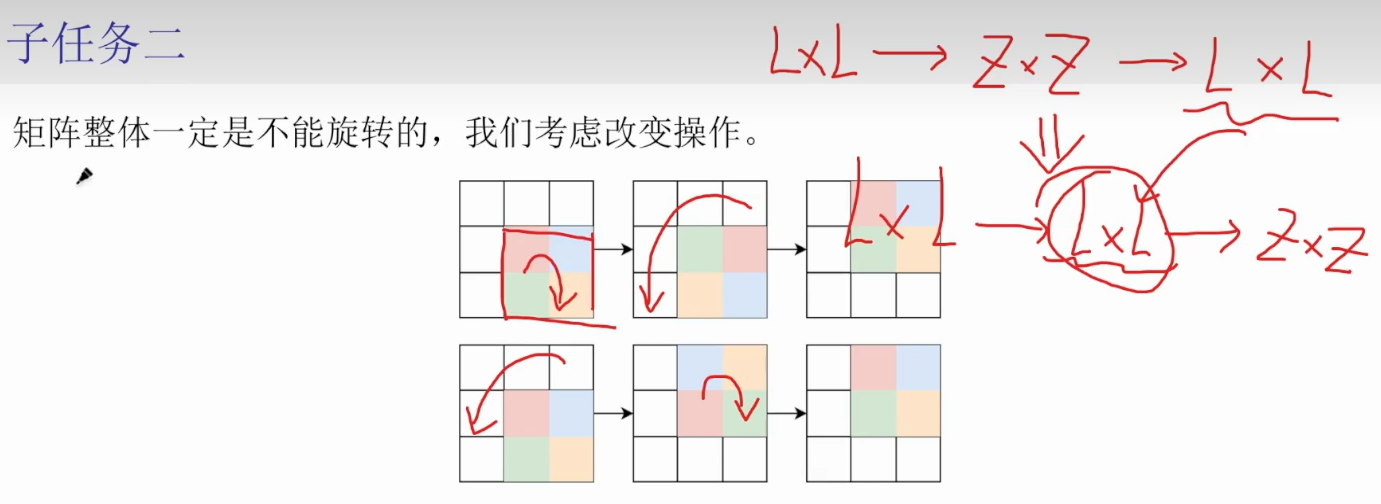
每次操作先不真正对矩阵整体进行翻转（时间复杂度太高），而是记录整体旋转的度数（或者顺时针转90度的次数），根据这个记录tag重新找到真正要旋转/翻转的小矩阵的位置，最后的最后再对矩阵整体进行旋转，感觉有点复杂，目前未实现代码（网上也没搜到正解QwQ）
