这道题昨天一直卡在怎么区分两个车站是否在同一线路,题解给我提供了思路。
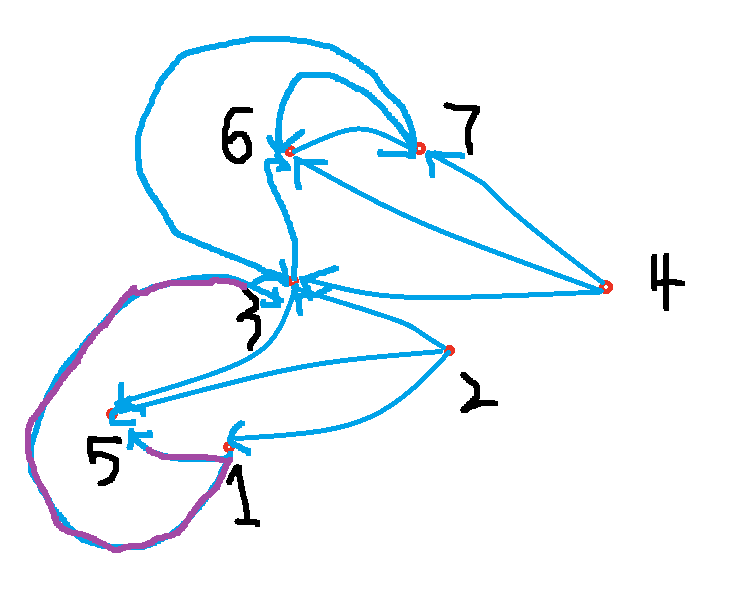
如下图所示(图丑,不要介意),对样例数据建一个有向图,如果在同一线路,线路靠前的站点可以到达后面的站点,比如线路1站点信息是"6 7",站点6能到站点7,所以站点6到站点7有一条单向边;又比如线路3站点信息是"2 1 3 5",站点2可以到站点1、3、5,站点1可以到站点3、5,站点3可以到站点5,所有根据此,我们可以画出从靠前站点出发到后面站点的单向边。之后,我们可以用Dijkstra算法,求站点1到站点7的最短路径。具体来说,我们用数组d计算站点1到各点的最短路径,初始化d[1]=0,所有边权都设为1。从站点1出发,可以先后走图中两条紫色的边,可以更新d[3]=1,d[5]=1。随后,对于站点3,到站点6有一条有向边,更新d[6]=2。站点5没有出边,过。然后是站点6,看线路1,可知站点6到站点7有一条有向边,更新站点7,d[7]=3。然后是站点7,没有更新其他站点,结束。
这个过程,如果在同一条线路上,可以以相同的值更新后面的站点(即换乘次数是一样的);和当前站点不在同一线路的点v是在当前步无法更新最小值的,要看这一轮入队的节点u有没有与v同属于另外一条线路,如果有,则d[v]=min(d[v],d[u]+1),这里的d[u]+1就表示了要换乘另一条路线,换乘次数加1。
另外要注意的是,从站点1更新其他站点的第一步应该是不需要换乘的,我们的步骤却加了一次换乘,所以最后答案要减1。
AC代码
cpp
#include<bits/stdc++.h>
#define maxn 505
using namespace std;
int m,n,ans,a[maxn],d[maxn];
vector<int> g[maxn];
bool vis[maxn];
void dij(){
memset(d,0x3f,sizeof(d));
d[1]=0;
priority_queue<pair<int,int> > q;
q.push({0,1});
while(q.size()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(d[v]>d[u]+1){
d[v]=d[u]+1;
q.push({-d[v],v});
}
}
}
}
int main(){
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++){
int cnt=0;
++cnt;
scanf("%d",&a[cnt]);
while(getchar()==' '){
++cnt;
scanf("%d",&a[cnt]);
}
for(int j=1;j<=cnt;j++){
for(int k=j+1;k<=cnt;k++){
g[a[j]].push_back(a[k]);
}
}
}
dij();
if(d[n]>m) printf("NO\n");
else printf("%d\n",d[n]-1);
return 0;
} 这道题先以车站1和五个亲戚所在的车站为起点,各跑一次Dijkstra算法,用二维数组d存储以这些这站为起点到各点的最短路径。然后,我们搜索五个亲戚所有可能的访问序列,求出访问五个亲戚的最短时间,这里可以用dfs来求。在这里要注意一下细节,n的数据规模是50000,在使用二维数组d来存储最短路径时,如果第一维表示的是亲戚和佳佳,第二维是亲戚或佳佳到这n个点的最短距离,那第一维就不要开太大,可以就开10个空间,d[0]表示佳佳,d[1]-d[5]表示5个亲戚。在写dfs时要注意第i个亲戚到第s个亲戚的最短距离就表示为d[s][a[j]]。
AC代码
cpp
#include<bits/stdc++.h>
#define maxn 50005
using namespace std;
int n,m,a[maxn],d[6][maxn],ans=0x3f3f3f3f;
vector< pair<int,int> > g[maxn];
bool vis[maxn];
void dij(int s){
memset(vis,0,sizeof(vis));
d[s][a[s]]=0;
priority_queue< pair<int,int> > q;
q.push({0,a[s]});
while(q.size()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=0;i<g[u].size();i++){
int v=g[u][i].first;
int w=g[u][i].second;
if(d[s][u]+w<d[s][v]){
d[s][v]=d[s][u]+w;
q.push({-d[s][v],v});
}
}
}
}
void dfs(int s,int k,int cost){
//cout<<cost<<endl;
if(k==6){
ans=min(ans,cost);
return;
}
for(int i=1;i<=5;i++){
if(vis[i]==0){
vis[i]=1;
dfs(i,k+1,cost+d[s][a[i]]);
vis[i]=0;
}
}
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=5;i++) scanf("%d",&a[i]);
a[0]=1;
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
g[u].push_back({v,w});
g[v].push_back({u,w});
}
memset(d,0x3f3f3f3f,sizeof(d));
for(int i=0;i<=5;i++) dij(i);
memset(vis,0,sizeof(vis));
vis[0]=1;
dfs(0,1,0);
printf("%d\n",ans);
return 0;
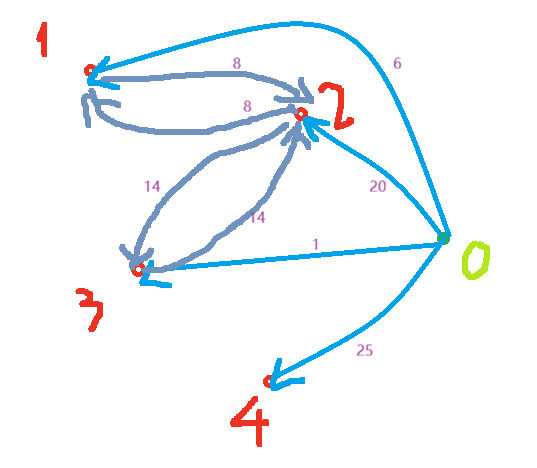
}这题很创新,我们可以建一个0号点,0号点到其他点第一条边,边权是其他点演唱会的价格,然后按照输入建立双向边,在这里因为涉及往返,所以直接把边权×2。我们通过求0号点到各点的最短距离从而求出从城市i出发去听演唱会的最低价格。
AC代码
cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll INF = (1LL<<62);
const int N = 200000 + 5;
int n, m;
ll dis[N];
bool vis[N];
struct Edge { int to; ll w; };
vector<Edge> g[N];
struct Node {
int u;
ll d;
bool operator < (const Node& other) const { return d > other.d; } // 小根堆
};
void solve() {
cin >> n >> m;
for (int i = 0; i <= n; i++) g[i].clear();
for (int i = 0; i <= n; i++) dis[i] = INF, vis[i] = false;
for (int i = 1; i <= m; i++) {
int u, v;
ll w;
cin >> u >> v >> w;
// 关键:往返成本 => 每条路边权乘 2
g[u].push_back({v, 2 * w});
g[v].push_back({u, 2 * w});
}
for (int i = 1; i <= n; i++) {
ll a;
cin >> a;
// 关键:虚拟源点 0 选"听演唱会城市 i",一次性付票价 a[i]
g[0].push_back({i, a});
}
priority_queue<Node> q;
dis[0] = 0;
q.push({0, 0});
while (!q.empty()) {
int u = q.top().u;
ll d = q.top().d;
q.pop();
if (d != dis[u]) continue; // 关键:丢弃旧状态
if (vis[u]) continue;
vis[u] = true;
for (auto e : g[u]) {
int v = e.to;
ll w = e.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({v, dis[v]});
}
}
}
for (int i = 1; i <= n; i++) {
if (i > 1) cout << ' ';
cout << dis[i]; // 关键:dis[i] 就是 i 的最小往返总花费
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int _ = 1;
while (_--) solve();
return 0;
}这题也很有意思。我们枚举将电话线引到震中市所有可能的最大花费。写一个判断函数,判断函数里面建图,如果一条边的边权是≤当前枚举的花费的话,那建图里面这条边边权为0,否则边权1。然后我们以1为起点,跑Dijkstra算法,如果点1到点n的最短路径>k,说明用了免费的k对后,还有超出当前枚举的最大花费的,情况不成立,判断函数返回False。如果最短路径≤k,说明当前枚举的最大花费是可能的。考虑到n和m的规模,枚举的时候使用二分可以优化时间复杂度。AC代码如下:
cpp
#include<bits/stdc++.h>
#define maxn 1005
using namespace std;
vector<pair<int,int> > g[maxn];
int n,p,k,d[maxn],m2[maxn][maxn];
bool vis[maxn];
void dij(){
priority_queue<pair<int,int> > q;
memset(d,0x3f,sizeof(d));
d[1]=0;
q.push({0,1});
while(q.size()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=1;i<=n;i++){
int w=m2[u][i];
if(d[i]>w+d[u]){
d[i]=w+d[u];
q.push({-d[i],i});
}
}
}
}
bool check(int mid){
memset(vis,0,sizeof(vis));
memset(m2,0x3f,sizeof(m2));
for(int i=1;i<=n;i++){
for(int j=0;j<g[i].size();j++){
int u=g[i][j].first;
int w=g[i][j].second;
if(w<=mid){
m2[i][u]=0;
m2[i][u]=0;
}
else{
m2[i][u]=1;
m2[i][u]=1;
}
}
}
dij();
if(d[n]>k) return 0;
return 1;
}
int main(){
scanf("%d%d%d",&n,&p,&k);
int l=0,r=0;
for(int i=1;i<=p;i++){
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
r=max(r,w);
g[a].push_back({b,w});
g[b].push_back({a,w});
}
r++;
if(p<=k) printf("0\n");
else{
if(check(r)==0) printf("-1\n");
else{
while(l+1<r){
int mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid;
}
printf("%d\n",l+1);
}
}
return 0;
}这题也是二分+最短路。在这里,我们枚举所有可能的最大花费,其中l是取不到的,就去点1的费用-1,r是可以取到的。在跑Dijkstra时,如果f[i]>枚举的最大费用那这个点无法访问,continue。否则就看d[u]+w<=b(保证体力够)并且d[u]+w<d[v],满足则更新d[v]。AC代码如下:
cpp
#include<bits/stdc++.h>
#define maxn 10005
#define int long long
using namespace std;
int n,m,b,f[maxn],lj[maxn][maxn],d[maxn];
vector<pair<int,int> > g[maxn];
bool vis[maxn];
void dij(int mm){
memset(vis,0,sizeof(vis));
memset(d,0x3f,sizeof(d));
d[1]=0;
priority_queue<pair<int,int> > q;
q.push({0,1});
while(q.size()){
int u=q.top().second;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=0;i<g[u].size();i++){
int v=g[u][i].first,w=g[u][i].second;
if(f[v]>mm) continue;
if(d[u]+w<=b&&d[u]+w<d[v]){
d[v]=d[u]+w;
q.push({-d[v],v});
}
}
}
}
bool check(int mid){
dij(mid);
if(d[n]>b) return 0;
return 1;
}
signed main(){
int l=0,r=0;
scanf("%lld%lld%lld",&n,&m,&b);
for(int i=1;i<=n;i++){
scanf("%lld",&f[i]);
r=max(r,f[i]);
}
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%lld%lld%lld",&u,&v,&w);
g[u].push_back({v,w});
g[v].push_back({u,w});
}
r++;
if(check(r)==0){
printf("AFK");
return 0;
}
l=f[1]-1;
r--;
while(l+1<r){
int mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid;
}
printf("%lld",r);
return 0;
}