一.最小生成树
核心目标:
"连通所有顶点,总权值最小",连通无向网的核心问题)
先明确3个前提定义
生成树:对于连通无向图,包含图中所有
n个顶点和n-1条边的无环连通子图
删一条边则不连通,加一条边则成环
最小生成树:顾名思义是1:n关系
最小生成树(MST):在连通无向带权图(网)中,所有生成树中边的权值之和最小的生成树,称为最小生成树。
核心需求:
用最少的"成本"(总权值),连接所有的"节点"(顶点),适用于"连通问题"(如修路、架线、网络布线)
属性

二.Kruskal算法(找边)
1.引申
由此算法引出最后一个图的存储结构 :
边集数组:
存储了边的两个端点及权值(多个顶点对组成的数组)
这里由邻接矩阵转换成边集数组形式
2.核心思想
贪心算法,查找局部边,并查集思想,符合条件的弄成同一父节点
3.步骤
首先把顶点的索引和边的权值存储在边集数组中
在将边集数组进行排序
三.Prim算法(找顶点)
1.核心思想
贪心思想,查找局部顶点
2.步骤
定义三大数组(各顶点边的权值数组,待激活节点数组,已访问数组),动态维护节点信息
以一个顶点为头,将关联顶点的边进行相关的操作
其次激活全部节点 : 利用假设法,找到最符合条件的边的关联顶点,在以该顶点进行操作
(找关联的各个顶点,找各个顶点里最符合条件的那个,激活本身节点)
四.代码
1.Kruskal代码
1.1要点
1.2代码
.h
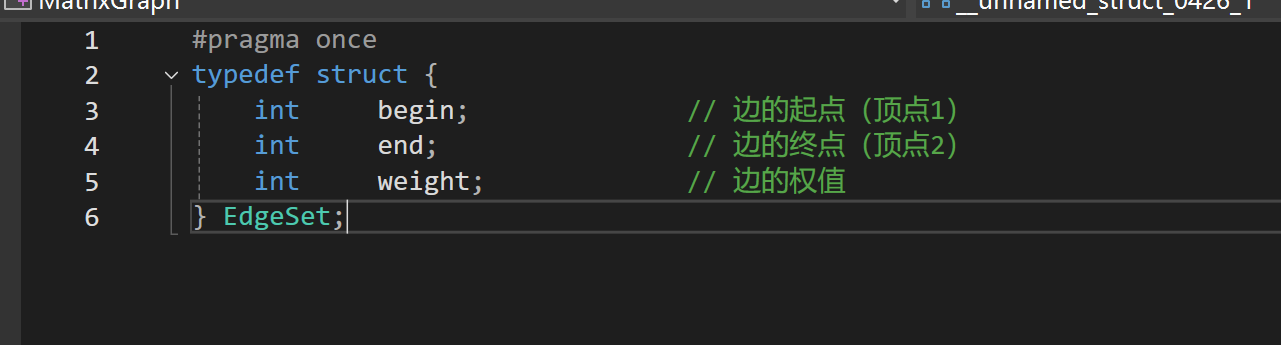
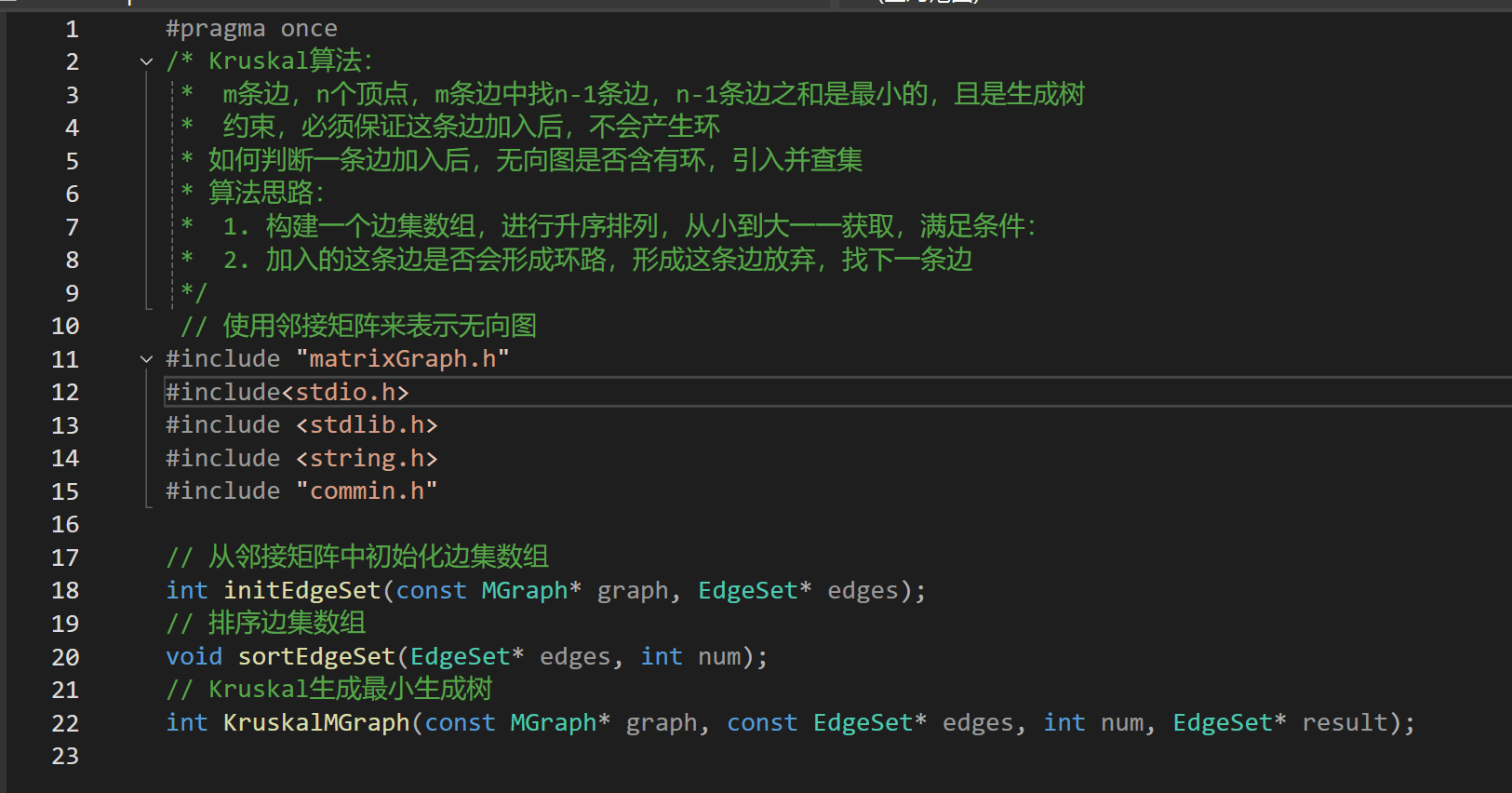
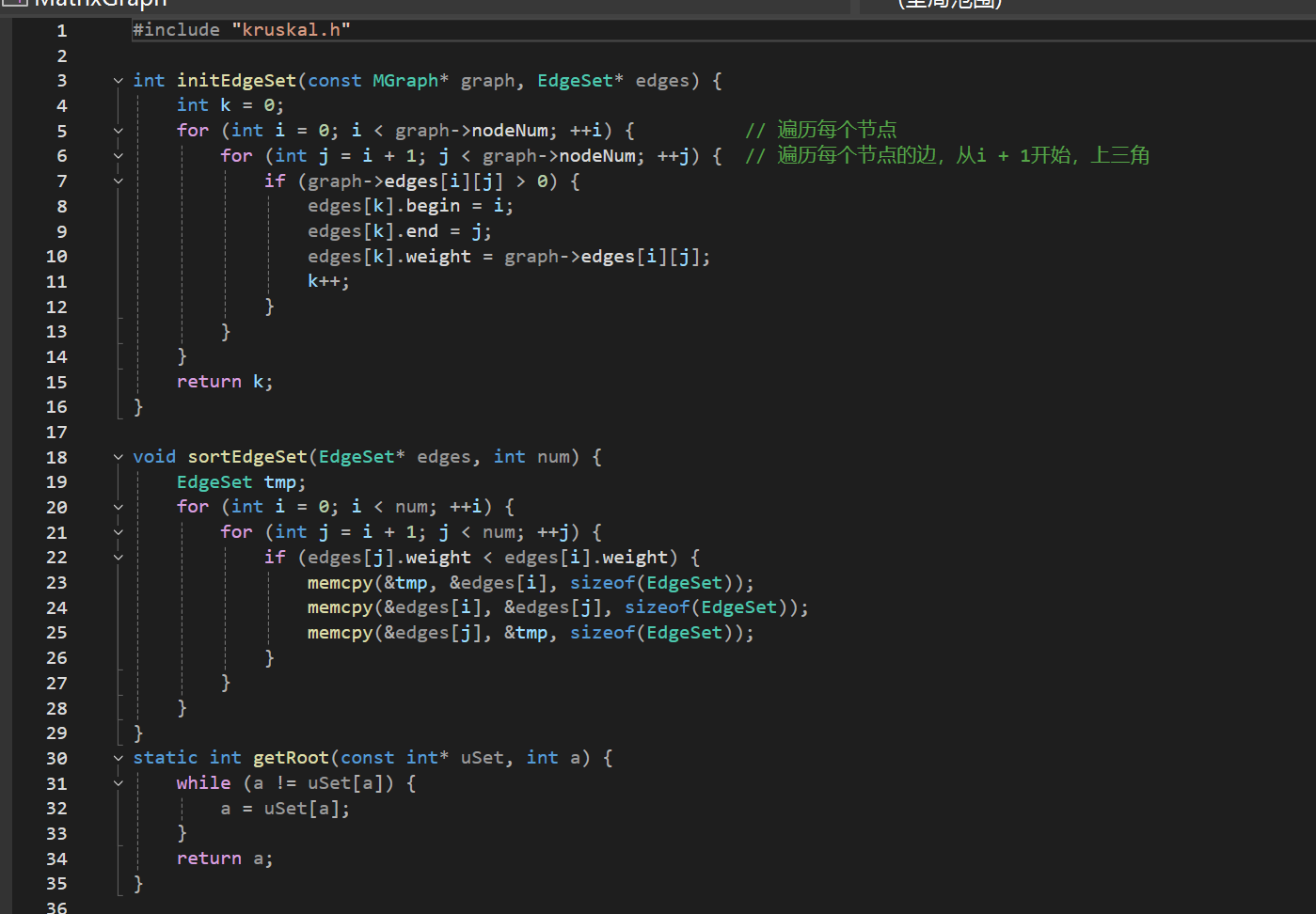
.c
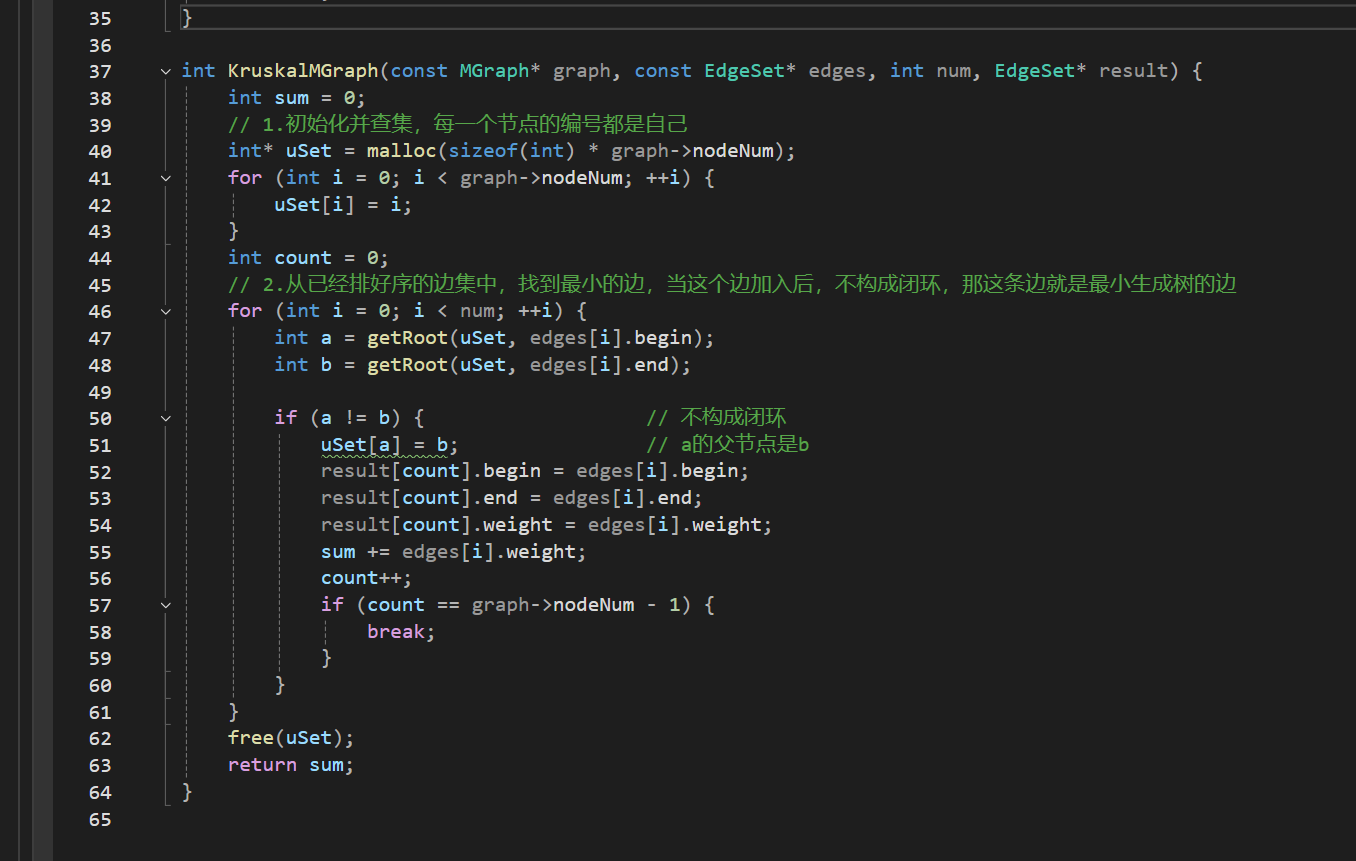
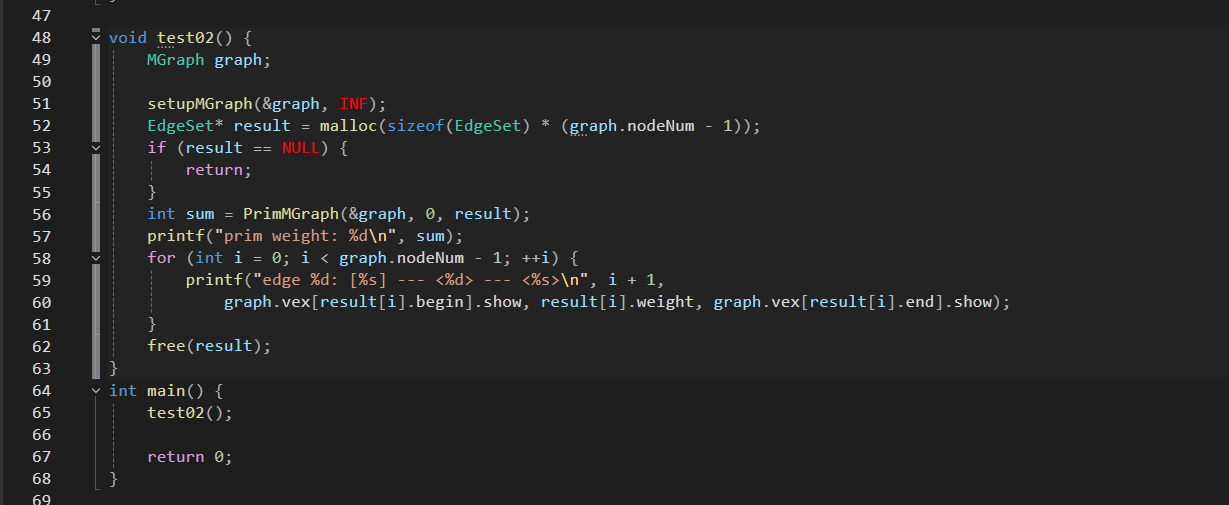
main.c
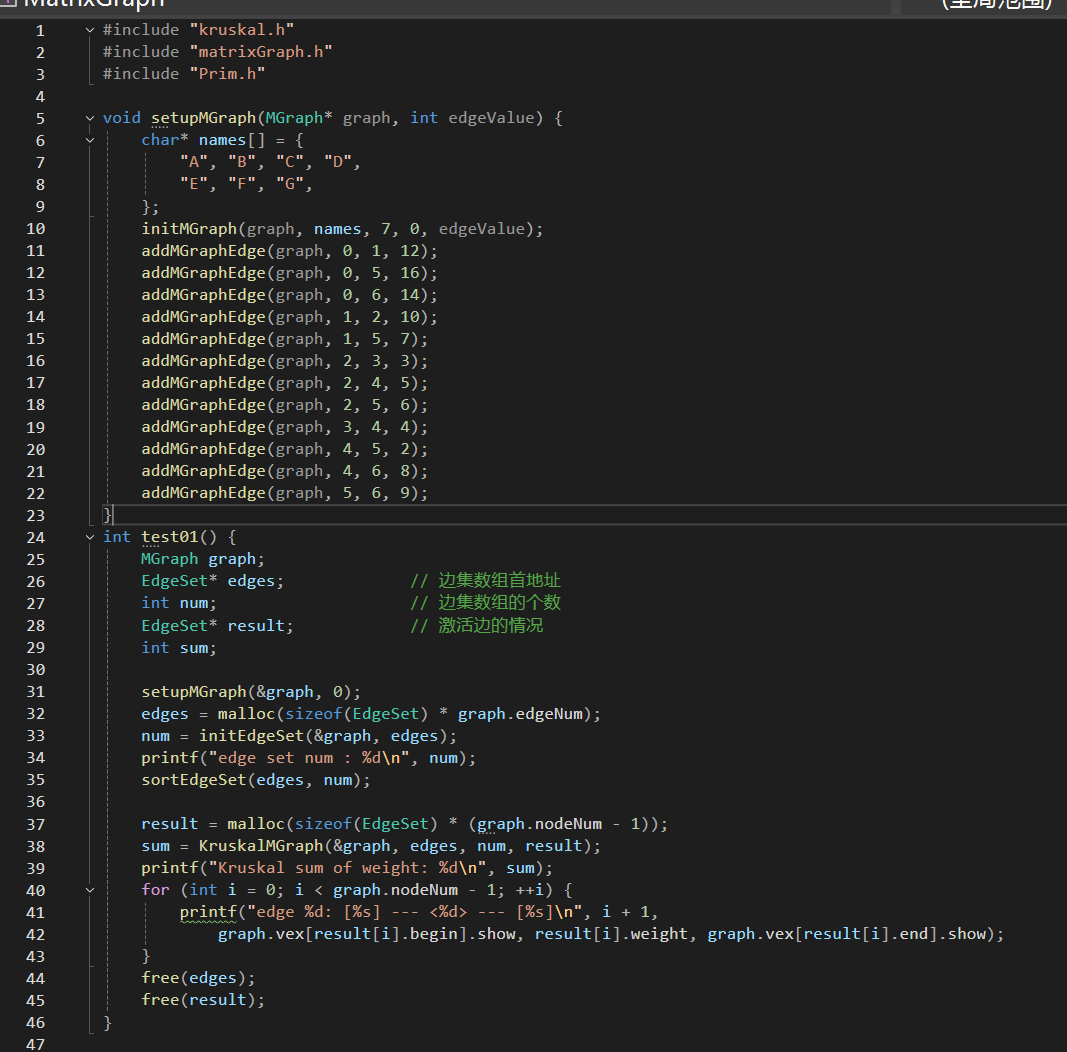
2.Prim代码
2.1要点
2.2代码
.h
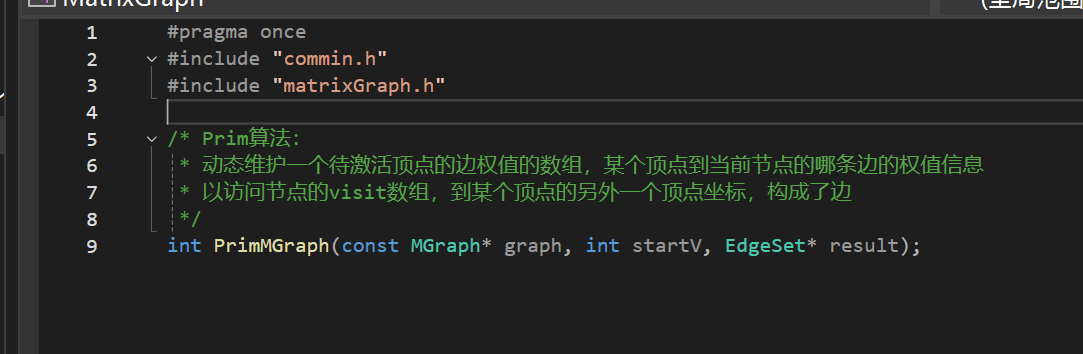
.c
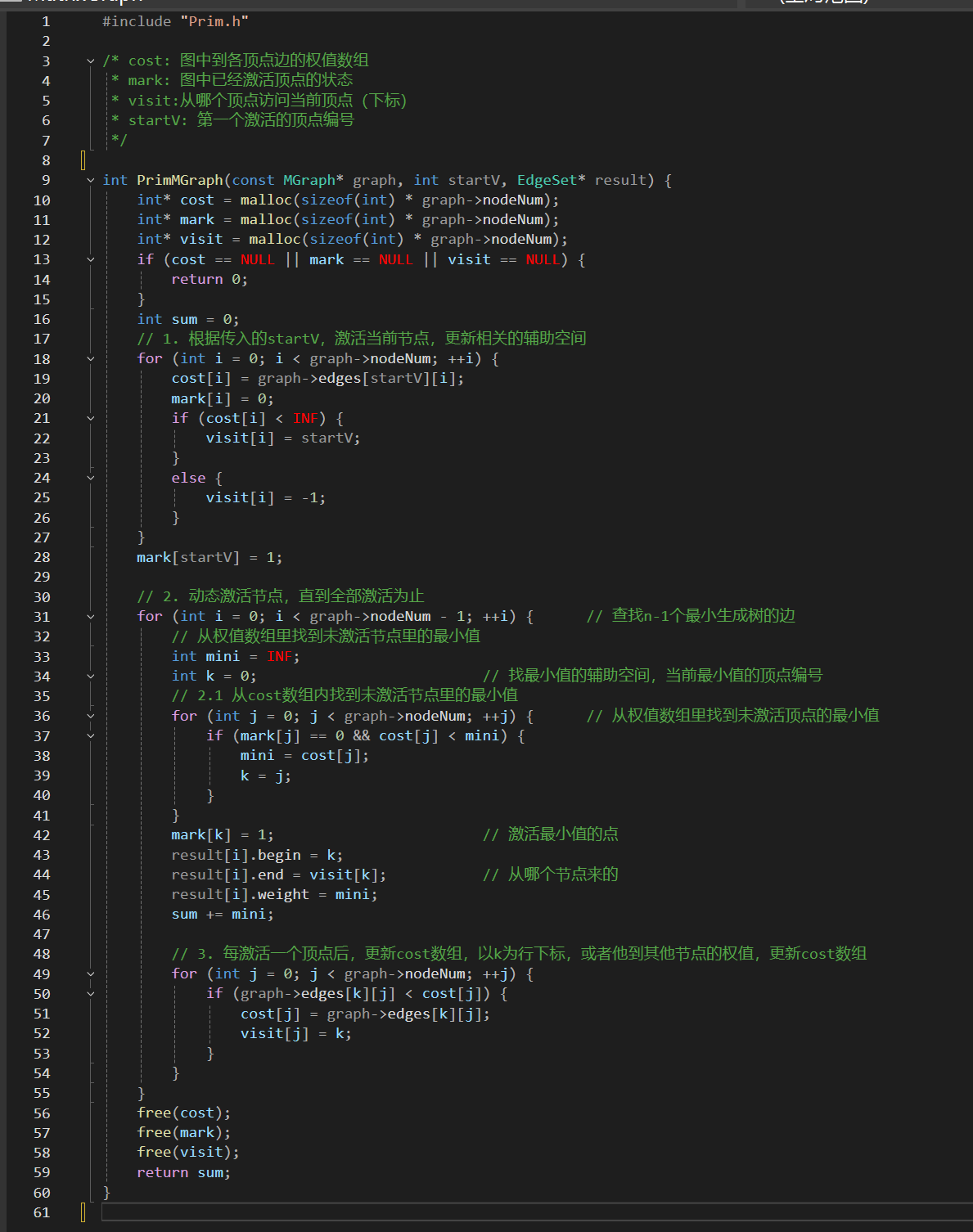
main.c