【算法通关指南：数据结构与算法篇】二叉树相关算法题：1.二叉树深度 2.求先序排列

🔥小龙报：个人主页

🎬作者简介：C++研发，嵌入式，机器人方向学习者

❄️个人专栏：《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录

• 前言
• 一、二叉树深度
• • 2.1题目
  • • [2.2 算法原理](#2.2 算法原理)
    • 2.3代码
• [二、 求先序排列](#二、 求先序排列)
• • 3.1题目
  • • [3.2 算法原理](#3.2 算法原理)
    • 3.3代码
• 总结与每日励志

前言

本专栏聚焦算法题实战，系统讲解算法模块：以《c++编程》，《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点，讲解思路与代码实现，帮助大家快速提升代码能力ps:本章节题目分两部分，比较基础笔者只附上代码供大家参考，其他的笔者会附上自己的思考和讲解，希望和大家一起努力见证自己的算法成长

---

一、二叉树深度

2.1题目

链接：二叉树深度

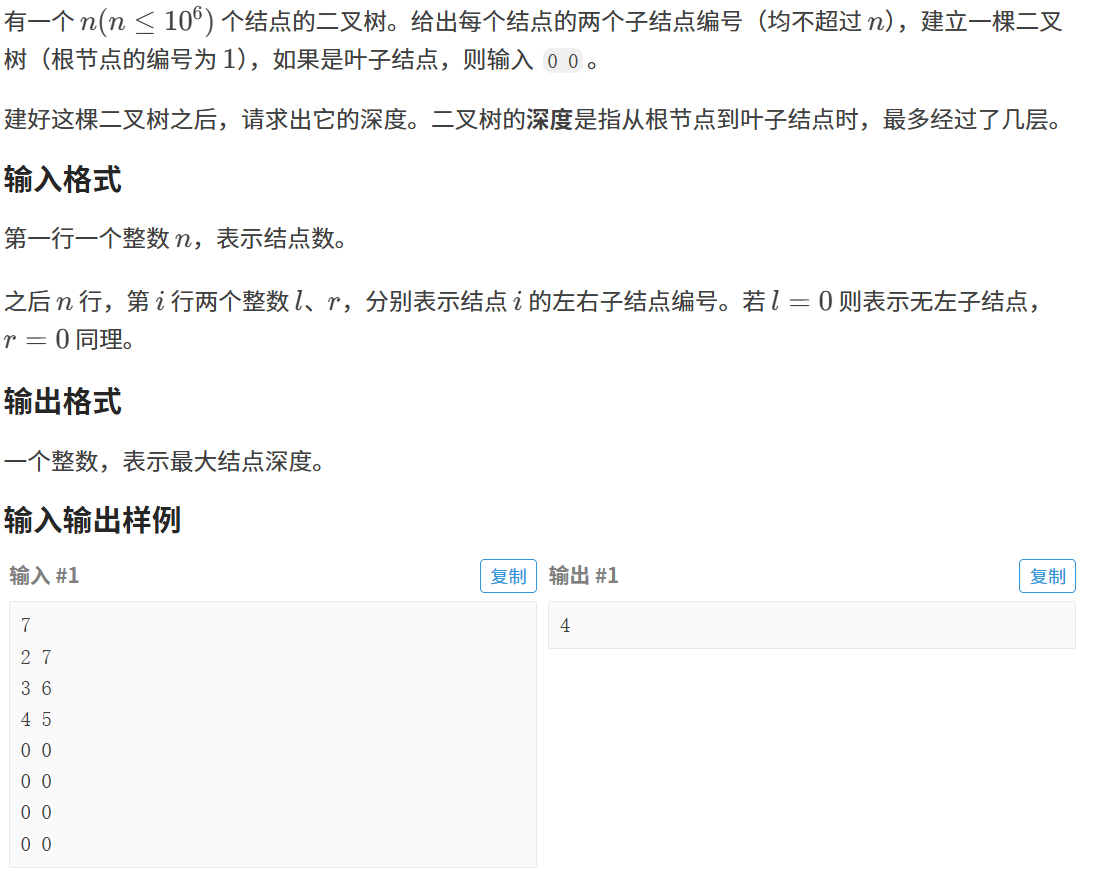
2.2 算法原理

二叉树的高度 = 1 + max(左子树的高度，右子树的高度)；因此，可以递归解决。

2.3代码

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int l[N], r[N];

int dfs(int root)
{
	if (!root)
		return 0;
	return max(dfs(l[root]), dfs(r[root])) + 1;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
		cin >> l[i] >> r[i];

	cout << dfs(1) << endl;
	return 0;
}

二、 求先序排列

3.1题目

链接：求先序排列

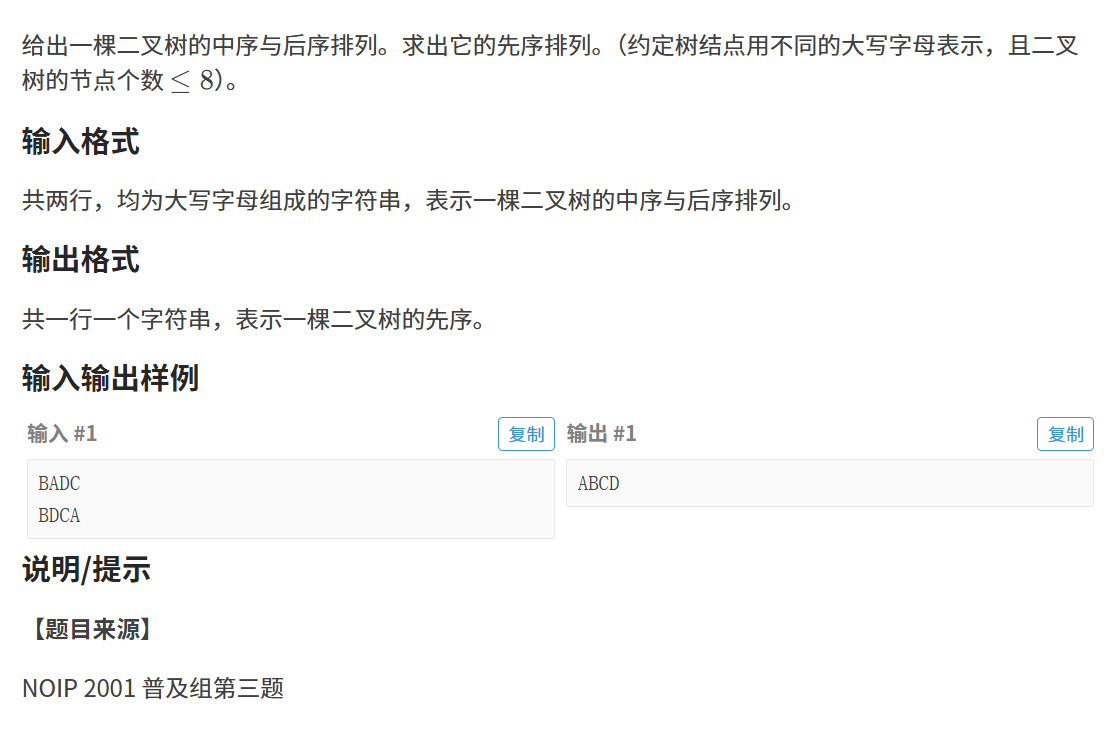
3.2 算法原理

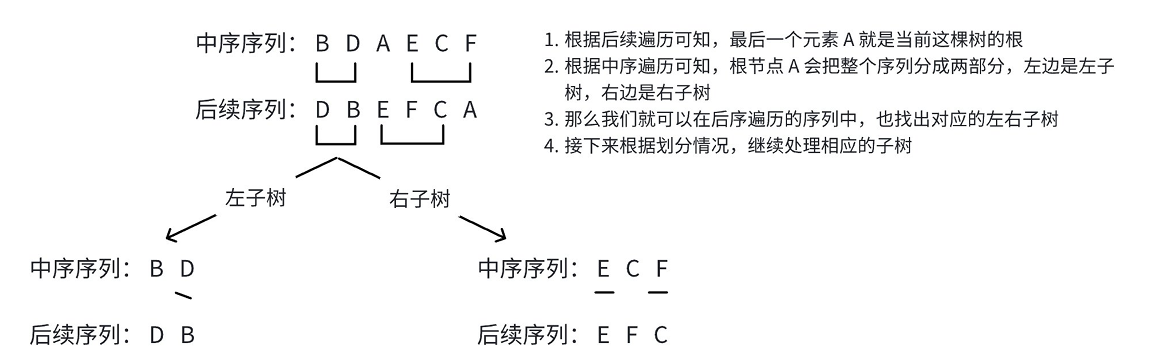
处理「左右字树」的方式与处理「原始序列」的方式一致，这样我们就可以用「递归」的方式求出先序序列
注： 如何进行区间定位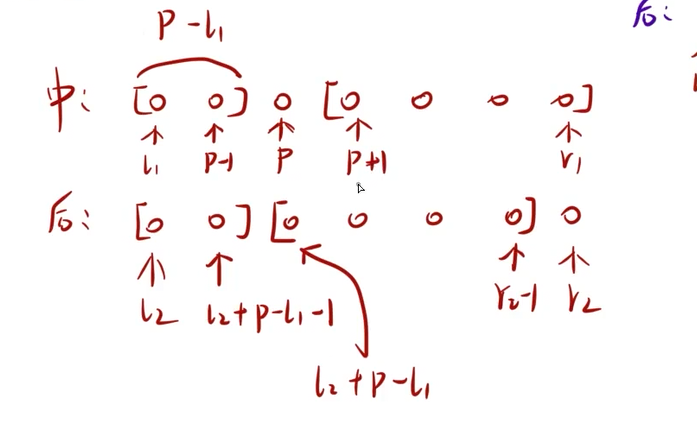

3.3代码

#include <iostream>
using namespace std;
string a, b;

void dfs(int l1, int r1, int l2, int r2)
{
	//递归出口
	if (r1 < l1)
		return;
	//确立根节点
	cout << b[r2];

	//寻找中序序列中的根节点划分左右子树
	int p = l1;
	while (a[p] != b[r2])
		p++;

	//递归处理左右子树
	dfs(l1, p - 1, l2, l2 + p - l1 - 1);
	dfs(p + 1, r1, l2 + p - l1, r2 - 1);
}

int main()
{
	cin >> a >> b;

	dfs(0, a.size() - 1, 0, b.size() - 1);
	return 0;
}

总结与每日励志

✨本次我们练习了二叉树深度和先序排列两道基础题，核心均运用递归思想：前者通过递归求左右子树高度取最大值加一得出结果，后者利用中序与后序序列定位根节点，递归处理左右子树完成先序输出。算法学习没有捷径，每一道题的积累都是成长的阶梯。永远相信美好的事情即将发生，坚持刷题、沉淀思路，终会突破瓶颈，在算法之路上稳步前行，不负每一份努力与热爱！