目录
[7.1 正态分类模型](#7.1 正态分类模型)
[完整代码 + 可视化](#完整代码 + 可视化)
[7.2 隐变量](#7.2 隐变量)
[7.3 期望最大化(EM)](#7.3 期望最大化(EM))
[7.4 混合高斯模型(GMM)](#7.4 混合高斯模型(GMM))
[7.4.1 混合高斯边缘化](#7.4.1 混合高斯边缘化)
[7.4.2 基于 EM 的混合模型拟合](#7.4.2 基于 EM 的混合模型拟合)
[完整代码 + 可视化(对比单高斯 vs GMM)](#完整代码 + 可视化(对比单高斯 vs GMM))
[7.5 t 分布](#7.5 t 分布)
[7.5.1 学生 t 分布边缘化](#7.5.1 学生 t 分布边缘化)
[7.5.2 拟合 t 分布的 EM](#7.5.2 拟合 t 分布的 EM)
[完整代码 + 可视化(对比正态分布 vs t 分布抗异常值能力)](#完整代码 + 可视化(对比正态分布 vs t 分布抗异常值能力))
[7.6 因子分析](#7.6 因子分析)
[7.6.1 因子分析的边缘分布](#7.6.1 因子分析的边缘分布)
[7.6.2 因子分析学习的 EM](#7.6.2 因子分析学习的 EM)
[完整代码 + 可视化(因子分析降维 vs PCA)](#完整代码 + 可视化(因子分析降维 vs PCA))
[7.7 组合模型](#7.7 组合模型)
[7.8 期望最大化算法的细节](#7.8 期望最大化算法的细节)
[7.8.1 EM 的下界](#7.8.1 EM 的下界)
[7.8.2 E 步](#7.8.2 E 步)
[7.8.3 M 步](#7.8.3 M 步)
[7.9 应用(核心实战)](#7.9 应用(核心实战))
[7.9.1 人脸检测](#7.9.1 人脸检测)
[7.9.2 目标识别](#7.9.2 目标识别)
[7.9.3 分割](#7.9.3 分割)
[分割实战代码 + 可视化](#分割实战代码 + 可视化)
[7.9.4 正脸识别](#7.9.4 正脸识别)
[7.9.5 改变人脸姿态(回归)](#7.9.5 改变人脸姿态(回归))
[7.9.6 作为隐变量的变换](#7.9.6 作为隐变量的变换)
前言

大家好!今天我们来拆解《计算机视觉:模型、学习和推理》的第 7 章 ------ 复杂数据密度建模。这一章核心解决的是 "怎么用数学模型描述复杂分布的数据",比如人脸数据、自然图像这些不是简单正态分布的数据集。
我会尽量把抽象概念讲得接地气,每个核心知识点都配可直接运行的 Python 代码 (Mac 系统适配)+ 可视化对比图,让大家不仅懂原理,还能亲手跑通案例。
7.1 正态分类模型
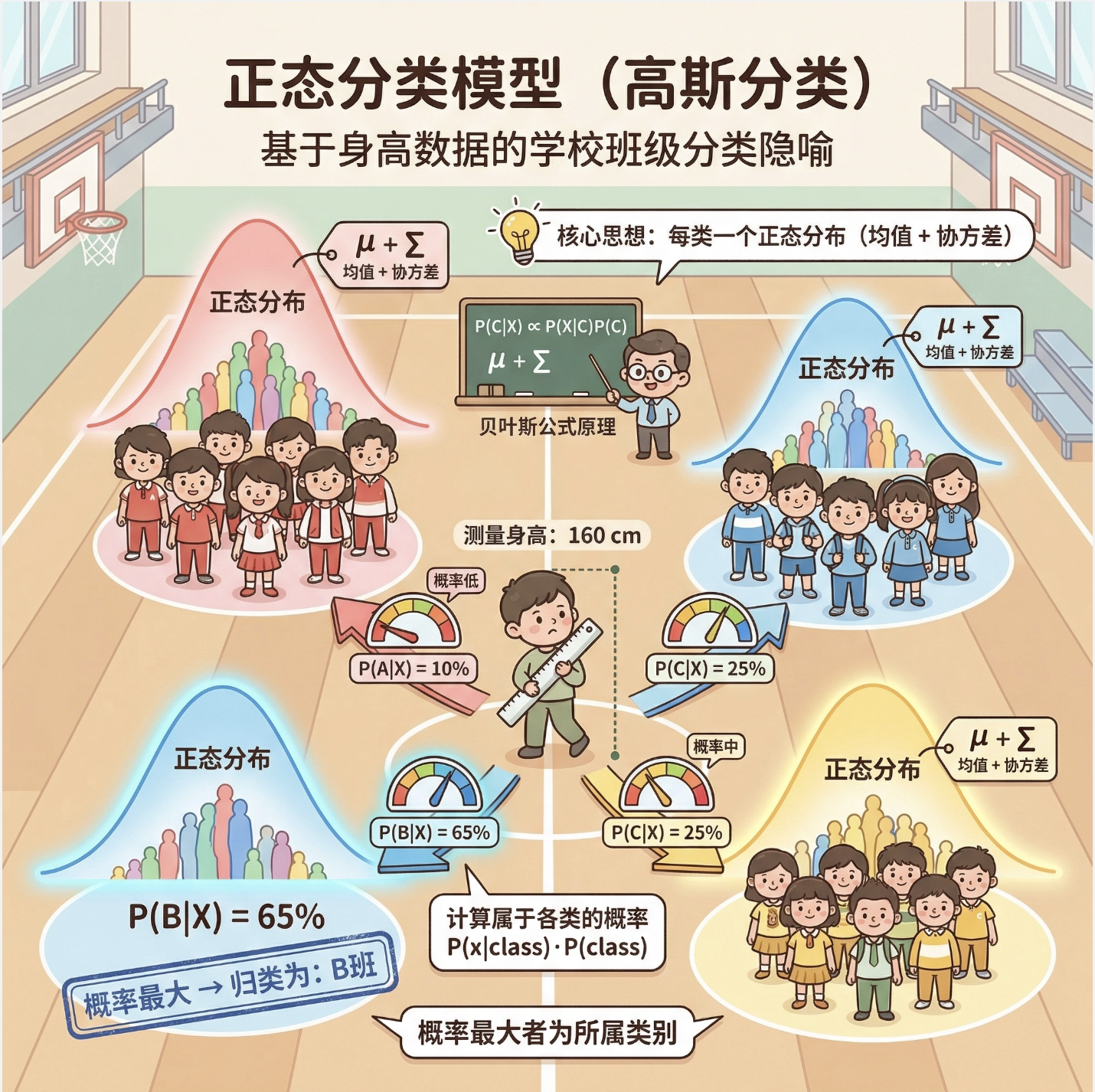
核心概念
正态分类模型(也叫高斯分类模型)是最简单的密度建模方式 ------ 假设每个类别的数据都服从单峰正态分布 ,就像每个班级的学生身高,都围绕着各自的平均值上下波动。
它的核心逻辑:
- 给每个类别分配一个正态分布(均值 + 协方差)
- 新数据来了,计算它属于每个分布的概率,概率最大的就是所属类别
完整代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
# ========== Mac系统Matplotlib中文配置 ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ========== 生成模拟数据 ==========
# 类别1:均值(2,2),协方差[[1,0.5],[0.5,1]]
np.random.seed(42) # 固定随机种子,结果可复现
class1 = np.random.multivariate_normal([2, 2], [[1, 0.5], [0.5, 1]], 200)
# 类别2:均值(6,6),协方差[[1,-0.5],[-0.5,1]]
class2 = np.random.multivariate_normal([6, 6], [[1, -0.5], [-0.5, 1]], 200)
# ========== 拟合正态分类模型 ==========
# 计算每个类别的均值和协方差
mu1 = np.mean(class1, axis=0)
cov1 = np.cov(class1, rowvar=False)
mu2 = np.mean(class2, axis=0)
cov2 = np.cov(class2, rowvar=False)
# 生成概率密度网格
x, y = np.meshgrid(np.linspace(0, 8, 100), np.linspace(0, 8, 100))
pos = np.dstack((x, y))
pdf1 = multivariate_normal.pdf(pos, mean=mu1, cov=cov1)
pdf2 = multivariate_normal.pdf(pos, mean=mu2, cov=cov2)
# ========== 可视化对比 ==========
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
# 子图1:原始数据分布
ax[0].scatter(class1[:,0], class1[:,1], c='skyblue', label='类别1', alpha=0.7)
ax[0].scatter(class2[:,0], class2[:,1], c='salmon', label='类别2', alpha=0.7)
ax[0].set_title('原始数据分布')
ax[0].set_xlabel('特征1')
ax[0].set_ylabel('特征2')
ax[0].legend()
ax[0].grid(alpha=0.3)
# 子图2:正态分类模型拟合结果
ax[1].contour(x, y, pdf1, levels=10, colors='skyblue', alpha=0.7, label='类别1分布')
ax[1].contour(x, y, pdf2, levels=10, colors='salmon', alpha=0.7, label='类别2分布')
ax[1].scatter(mu1[0], mu1[1], c='blue', marker='*', s=200, label='类别1均值')
ax[1].scatter(mu2[0], mu2[1], c='red', marker='*', s=200, label='类别2均值')
ax[1].set_title('正态分类模型拟合结果')
ax[1].set_xlabel('特征1')
ax[1].set_ylabel('特征2')
ax[1].legend()
ax[1].grid(alpha=0.3)
plt.tight_layout()
plt.show()运行效果
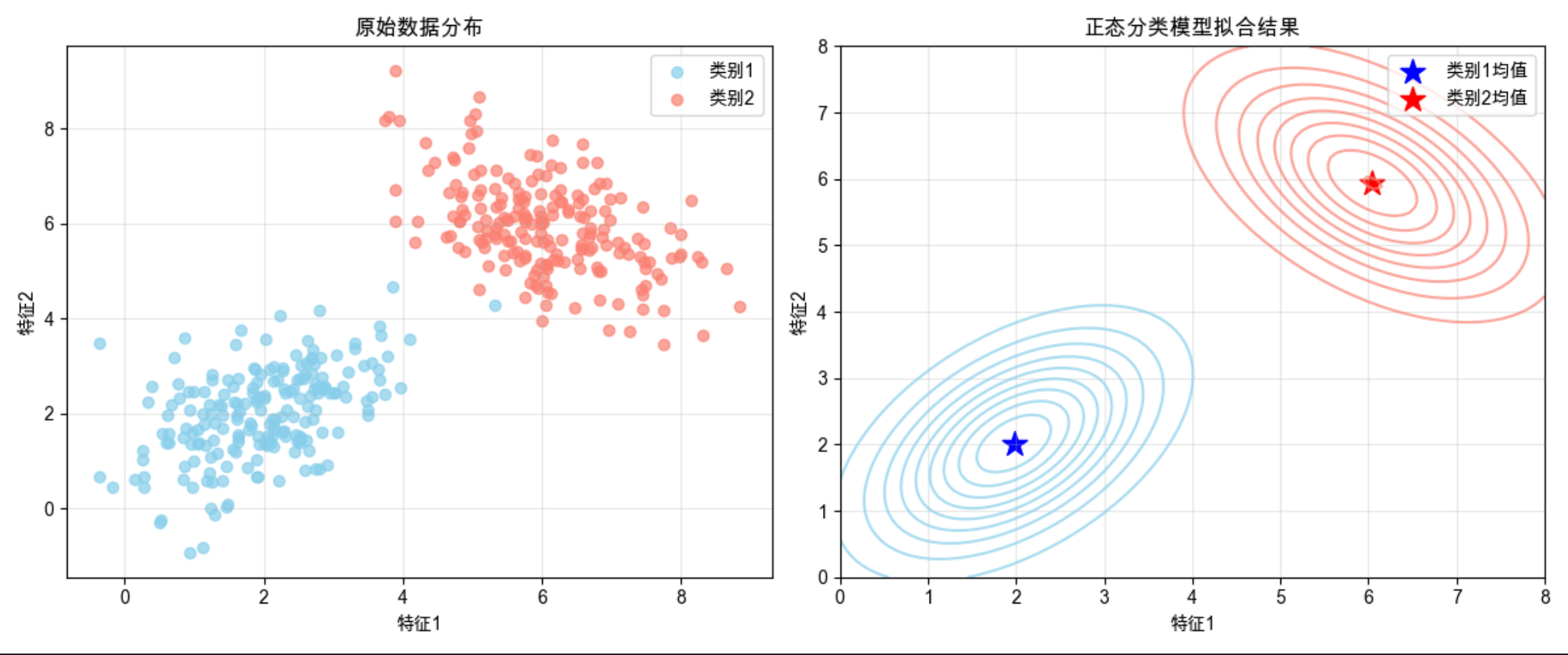
7.2 隐变量

核心概念
隐变量就是 "看不见但真实存在的变量"------ 比如你看到学生成绩忽高忽低(可观测),但背后的 "学习状态"(隐变量)你看不到,却能通过成绩推测。
在密度建模里,隐变量是破解 "复杂分布" 的关键:把一个复杂分布,拆成 "可观测变量 + 隐变量" 的组合,比如混合高斯模型里的 "数据属于哪个高斯分量" 就是隐变量。
通俗比喻
隐变量就像拼图的 "隐藏层":直接拼复杂图案很难,但先找到每个小块属于哪个区域(隐变量),再拼就简单了。
7.3 期望最大化(EM)

核心概念
EM 算法是解决 "有隐变量的模型拟合" 的 "万能钥匙",分两步循环跑,直到收敛:
1.E 步(期望步) :固定模型参数,算隐变量的后验概率(比如 "猜每个数据属于哪个高斯分量")
2.M 步(最大化步) :固定隐变量的概率,更新模型参数(比如 "用猜的归属重新算每个高斯的均值 / 协方差")
流程图
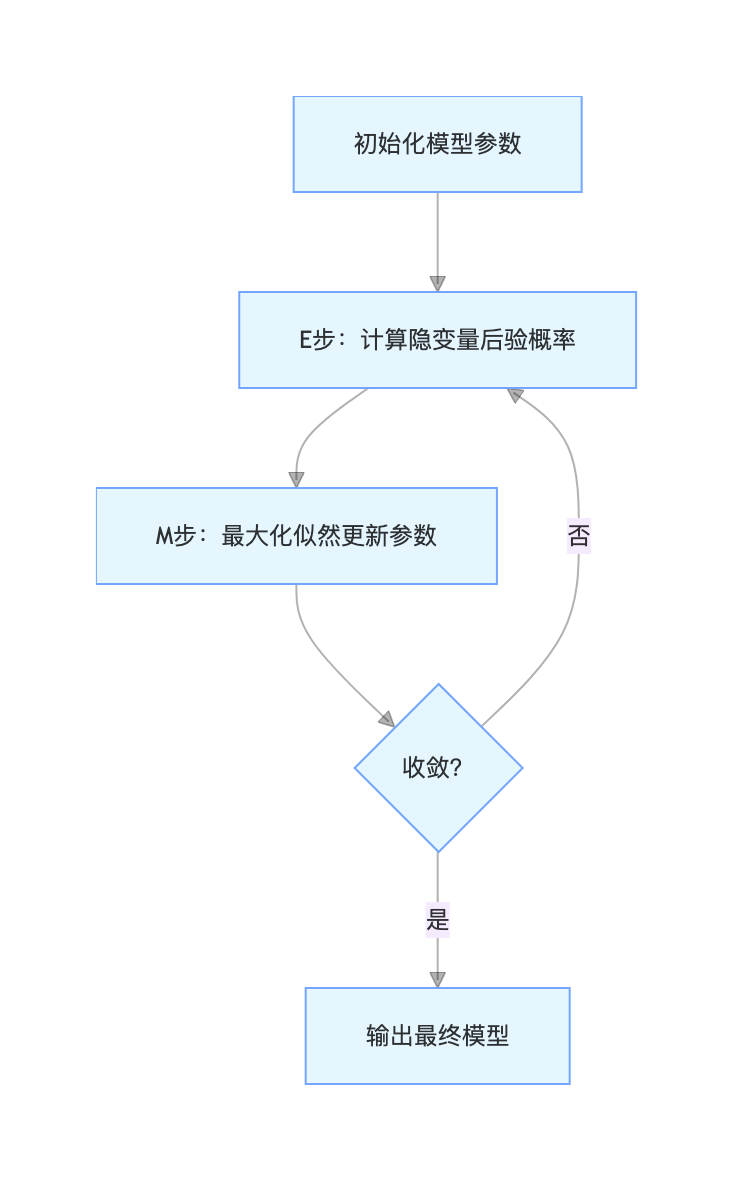
核心逻辑
EM 算法的本质是 "先猜后更":先猜隐变量的值,再用猜的值优化模型,再用优化后的模型重新猜,直到猜的结果和模型参数不再变化。
7.4 混合高斯模型(GMM)
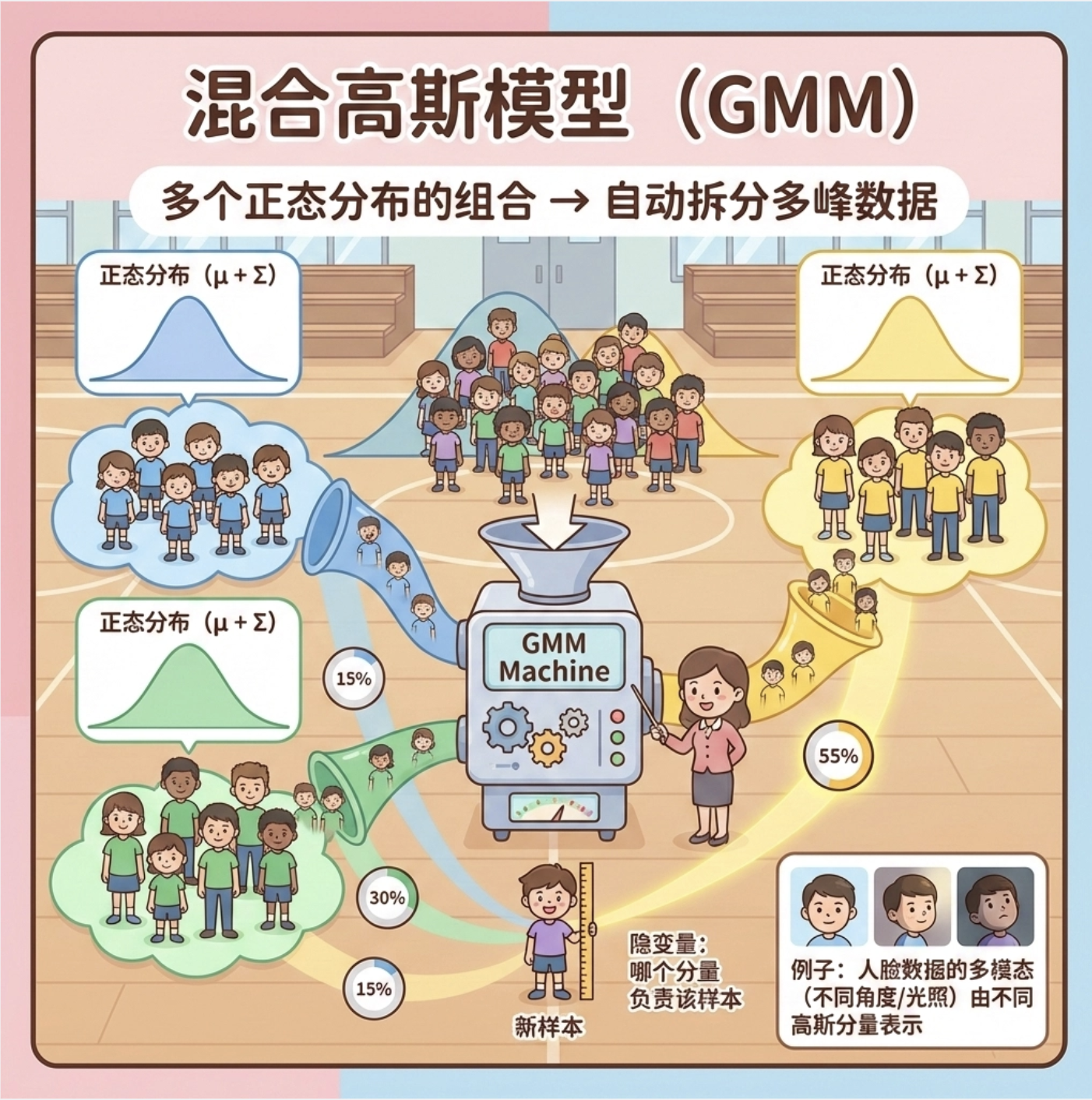
核心概念
单正态分布只能描述 "单峰" 数据,混合高斯模型(GMM)是多个正态分布的 "组合"------ 就像把多个班级的学生身高数据混在一起,GMM 能自动拆分出每个班级的分布。
比如人脸数据,不同角度、光照的人脸可以看作不同的高斯分量,GMM 能把这些分量都拟合出来。
7.4.1 混合高斯边缘化
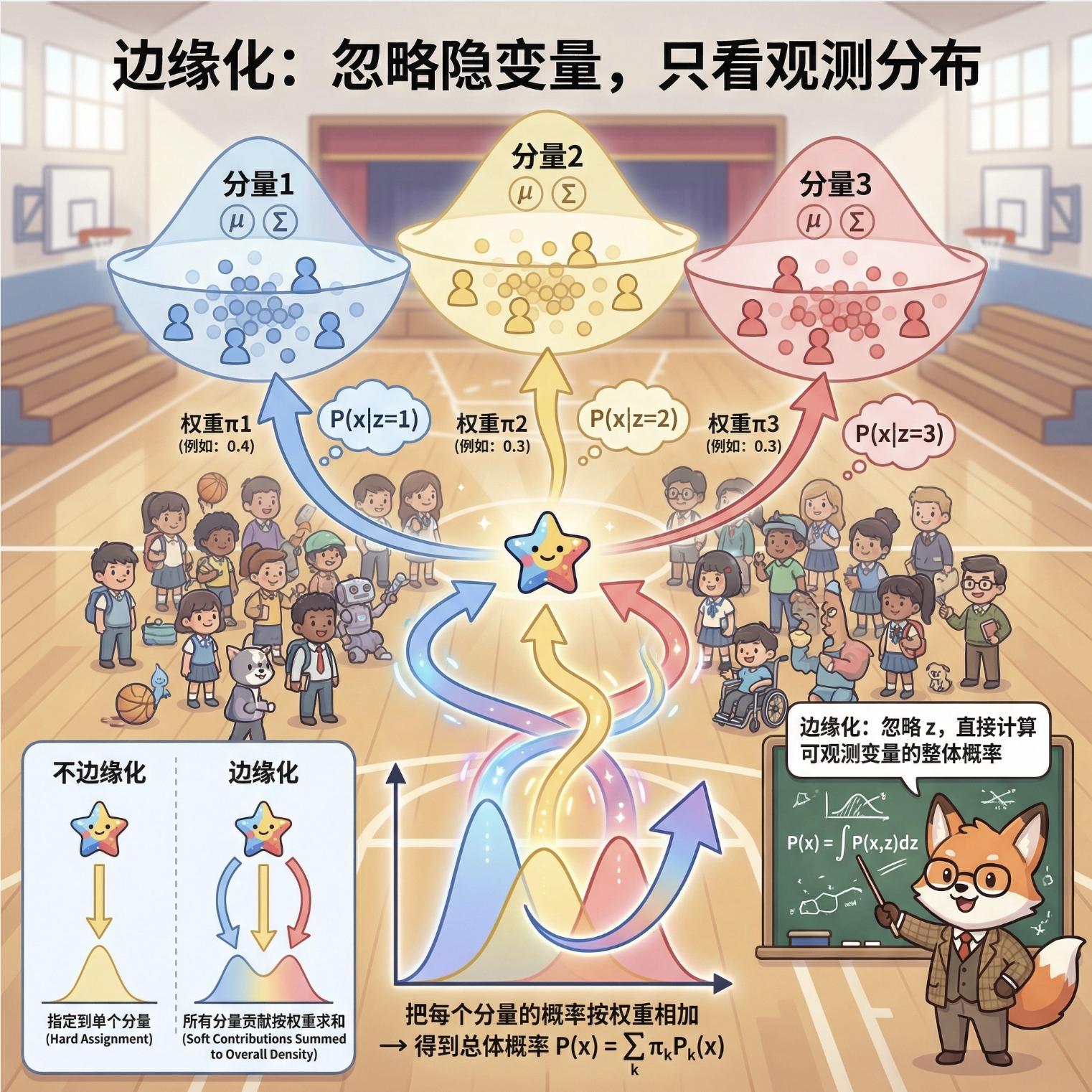
边缘化就是 "忽略隐变量,只看可观测变量的分布"------ 比如不管数据属于哪个高斯分量,只算它的整体概率(把每个分量的概率加权求和)。
7.4.2 基于 EM 的混合模型拟合
完整代码 + 可视化(对比单高斯 vs GMM)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from sklearn.mixture import GaussianMixture
# ========== Mac配置(同上) ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ========== 生成复杂分布数据(3个高斯分量混合) ==========
np.random.seed(42)
# 分量1:均值(1,1),协方差[[0.5,0],[0,0.5]],权重0.3
data1 = np.random.multivariate_normal([1,1], [[0.5,0],[0,0.5]], 150)
# 分量2:均值(4,5),协方差[[0.8,0.2],[0.2,0.8]],权重0.5
data2 = np.random.multivariate_normal([4,5], [[0.8,0.2],[0.2,0.8]], 250)
# 分量3:均值(7,2),协方差[[0.6,-0.1],[-0.1,0.6]],权重0.2
data3 = np.random.multivariate_normal([7,2], [[0.6,-0.1],[-0.1,0.6]], 100)
# 合并数据
data = np.vstack([data1, data2, data3])
# ========== 拟合单高斯 vs GMM ==========
# 单高斯拟合
mu_single = np.mean(data, axis=0)
cov_single = np.cov(data, rowvar=False)
# GMM拟合(3个分量)
gmm = GaussianMixture(n_components=3, random_state=42)
gmm.fit(data)
# ========== 可视化对比 ==========
x, y = np.meshgrid(np.linspace(0, 8, 100), np.linspace(0, 8, 100))
pos = np.dstack((x, y))
# 单高斯PDF
pdf_single = multivariate_normal.pdf(pos, mean=mu_single, cov=cov_single)
# GMM PDF(手动计算)
pdf_gmm = np.zeros_like(pdf_single)
for i in range(3):
pdf_gmm += gmm.weights_[i] * multivariate_normal.pdf(pos,
mean=gmm.means_[i],
cov=gmm.covariances_[i])
# 绘图
fig, ax = plt.subplots(1, 3, figsize=(18, 5))
# 子图1:原始混合数据
ax[0].scatter(data1[:,0], data1[:,1], c='skyblue', alpha=0.7)
ax[0].scatter(data2[:,0], data2[:,1], c='salmon', alpha=0.7)
ax[0].scatter(data3[:,0], data3[:,1], c='lightgreen', alpha=0.7)
ax[0].set_title('原始混合高斯数据')
ax[0].set_xlabel('特征1')
ax[0].set_ylabel('特征2')
ax[0].grid(alpha=0.3)
# 子图2:单高斯拟合(效果差)
ax[1].scatter(data[:,0], data[:,1], c='gray', alpha=0.5)
ax[1].contour(x, y, pdf_single, levels=10, colors='red', alpha=0.8)
ax[1].scatter(mu_single[0], mu_single[1], c='red', marker='*', s=200)
ax[1].set_title('单高斯拟合(效果差)')
ax[1].set_xlabel('特征1')
ax[1].set_ylabel('特征2')
ax[1].grid(alpha=0.3)
# 子图3:GMM拟合(效果好)
ax[2].scatter(data[:,0], data[:,1], c='gray', alpha=0.5)
ax[2].contour(x, y, pdf_gmm, levels=10, colors='blue', alpha=0.8)
# 标出GMM各分量均值
for i in range(3):
ax[2].scatter(gmm.means_[i,0], gmm.means_[i,1], c=['blue','red','green'][i],
marker='*', s=200)
ax[2].set_title('GMM拟合(3分量,效果好)')
ax[2].set_xlabel('特征1')
ax[2].set_ylabel('特征2')
ax[2].grid(alpha=0.3)
plt.tight_layout()
plt.show()运行效果
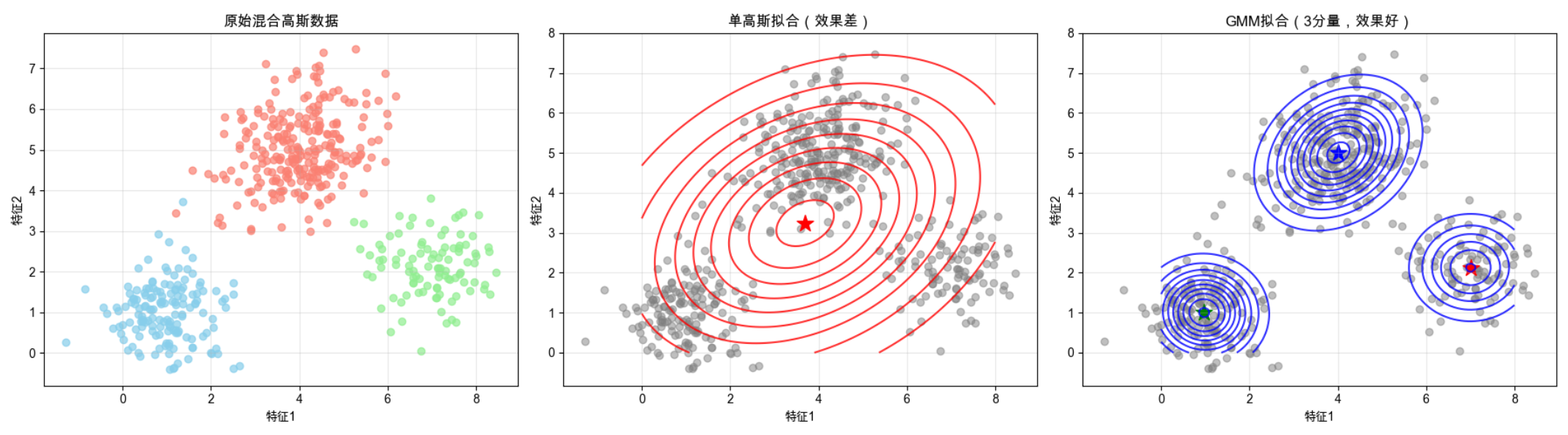
7.5 t 分布
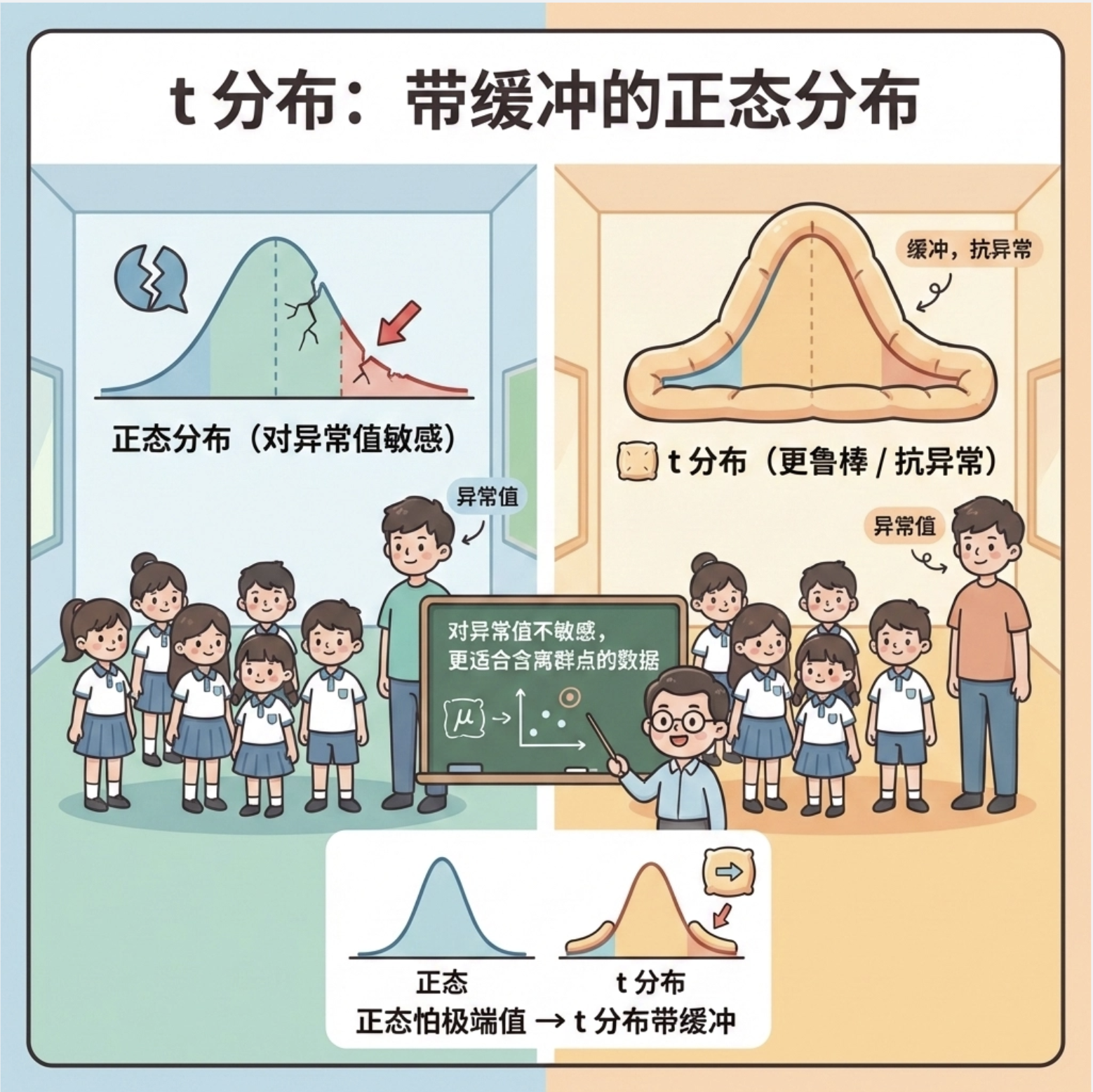
核心概念
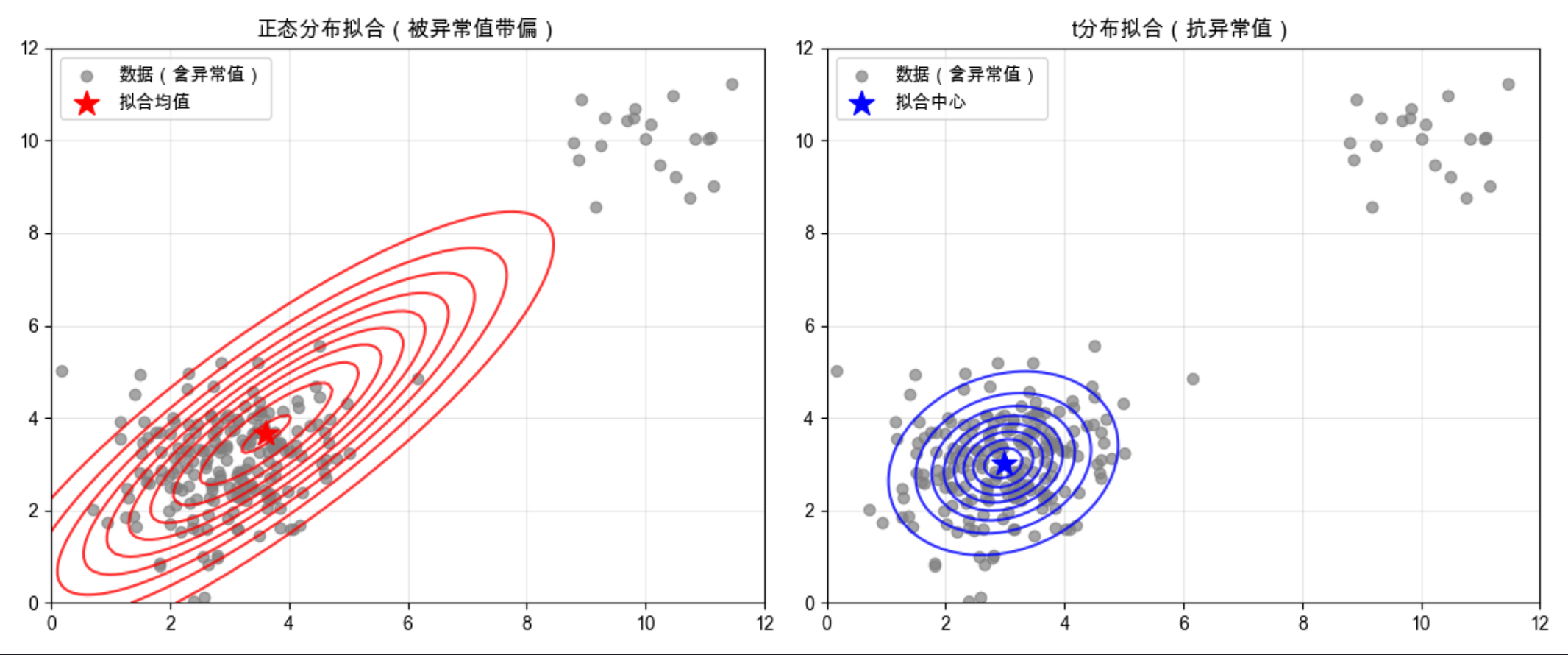
t 分布是 "抗造版" 的正态分布 ------ 正态分布怕异常值(比如班级里突然出现一个 2 米高的学生),t 分布对异常值不敏感,就像 "带了缓冲垫" 的正态分布。
7.5.1 学生 t 分布边缘化
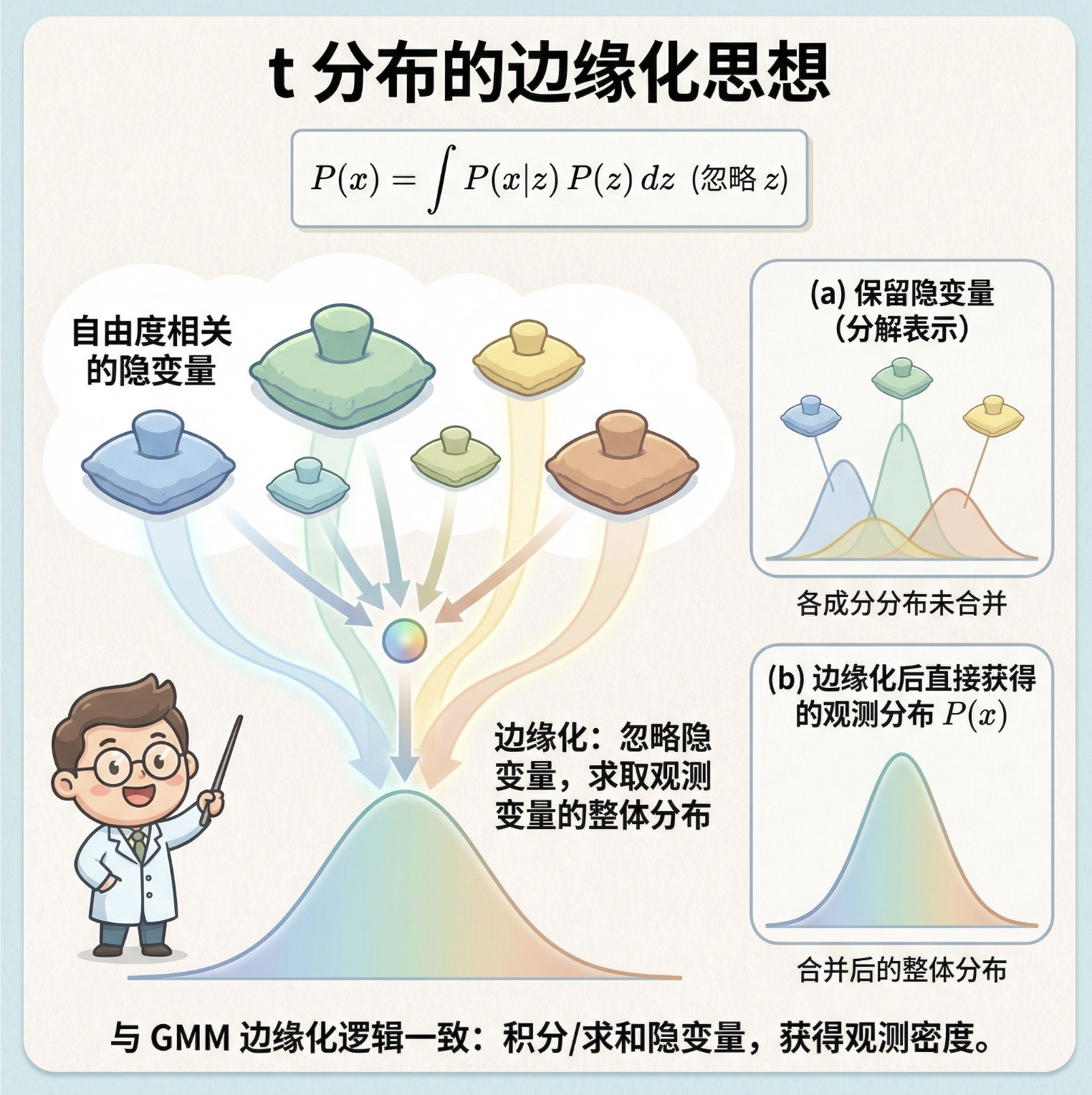
和混合高斯边缘化逻辑一致:忽略隐变量(t 分布的 "自由度相关隐变量"),计算可观测变量的整体分布。
7.5.2 拟合 t 分布的 EM
完整代码 + 可视化(对比正态分布 vs t 分布抗异常值能力)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_t, multivariate_normal
# ========== Mac配置 ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ========== 生成带异常值的数据 ==========
np.random.seed(42)
# 正常数据(正态分布)
normal_data = np.random.multivariate_normal([3,3], [[1,0.2],[0.2,1]], 200)
# 异常值(远离中心)
outliers = np.random.multivariate_normal([10,10], [[0.5,0],[0,0.5]], 20)
data = np.vstack([normal_data, outliers])
# ========== 拟合正态分布 vs t分布 ==========
# 正态分布拟合
mu_norm = np.mean(data, axis=0)
cov_norm = np.cov(data, rowvar=False)
# t分布拟合(自由度df=3,越小越抗异常)
t_fit = multivariate_t(loc=np.mean(normal_data, axis=0),
shape=np.cov(normal_data, rowvar=False),
df=3)
# ========== 可视化对比 ==========
x, y = np.meshgrid(np.linspace(0, 12, 100), np.linspace(0, 12, 100))
pos = np.dstack((x, y))
pdf_norm = multivariate_normal.pdf(pos, mean=mu_norm, cov=cov_norm)
pdf_t = t_fit.pdf(pos)
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
# 子图1:正态分布拟合(被异常值带偏)
ax[0].scatter(data[:,0], data[:,1], c='gray', alpha=0.7, label='数据(含异常值)')
ax[0].contour(x, y, pdf_norm, levels=10, colors='red', alpha=0.8, label='正态分布拟合')
ax[0].scatter(mu_norm[0], mu_norm[1], c='red', marker='*', s=200, label='拟合均值')
ax[0].set_title('正态分布拟合(被异常值带偏)')
ax[0].legend()
ax[0].grid(alpha=0.3)
# 子图2:t分布拟合(抗异常值)
ax[1].scatter(data[:,0], data[:,1], c='gray', alpha=0.7, label='数据(含异常值)')
ax[1].contour(x, y, pdf_t, levels=10, colors='blue', alpha=0.8, label='t分布拟合')
ax[1].scatter(t_fit.loc[0], t_fit.loc[1], c='blue', marker='*', s=200, label='拟合中心')
ax[1].set_title('t分布拟合(抗异常值)')
ax[1].legend()
ax[1].grid(alpha=0.3)
plt.tight_layout()
plt.show()运行效果
7.6 因子分析
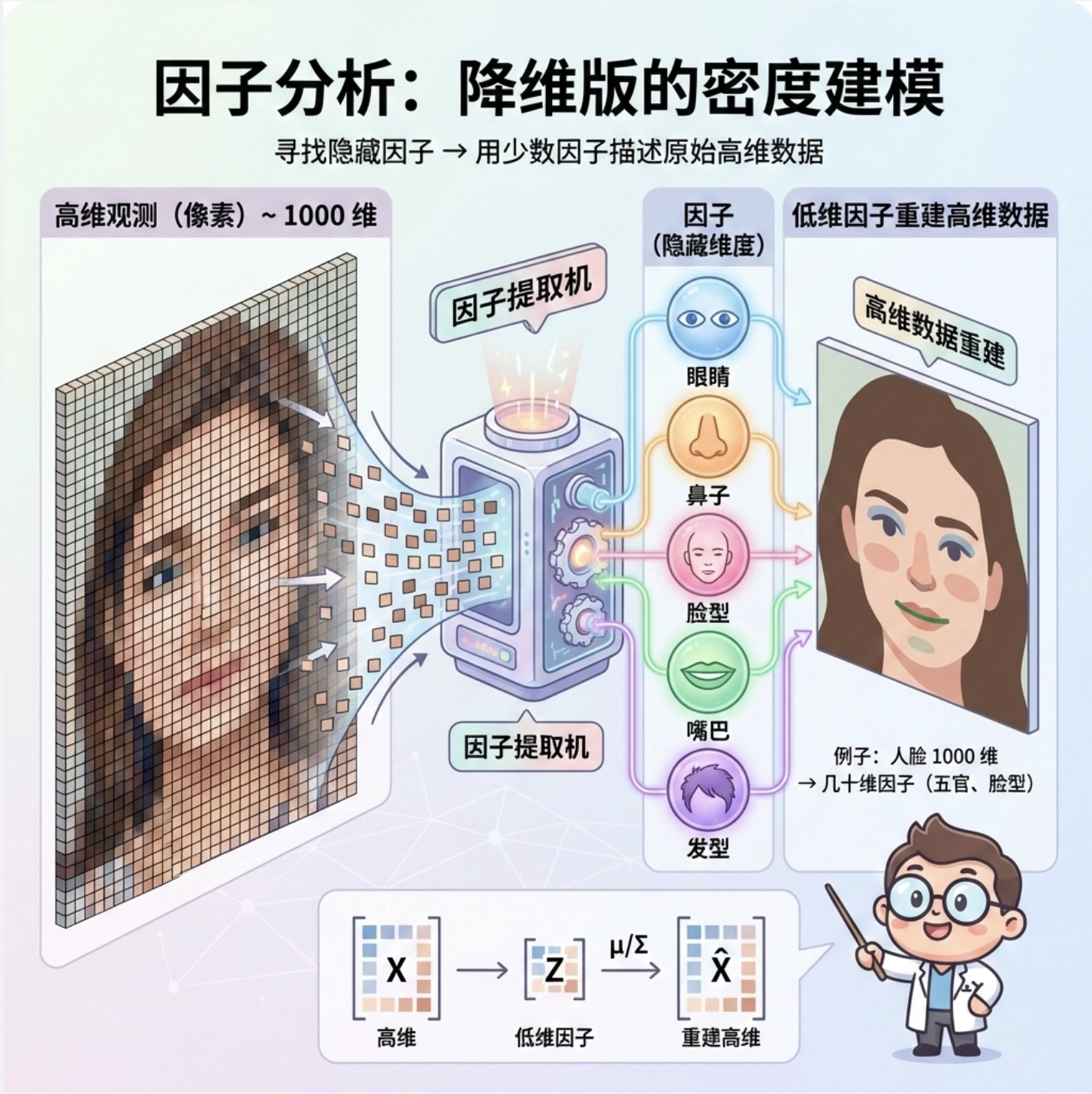
核心概念
因子分析是 "降维版" 的密度建模 ------ 比如人脸数据有 1000 个像素(1000 维),但核心特征(比如五官位置、脸型)只有几十维,因子分析能找到这些 "隐藏因子",用低维因子描述高维数据。
7.6.1 因子分析的边缘分布
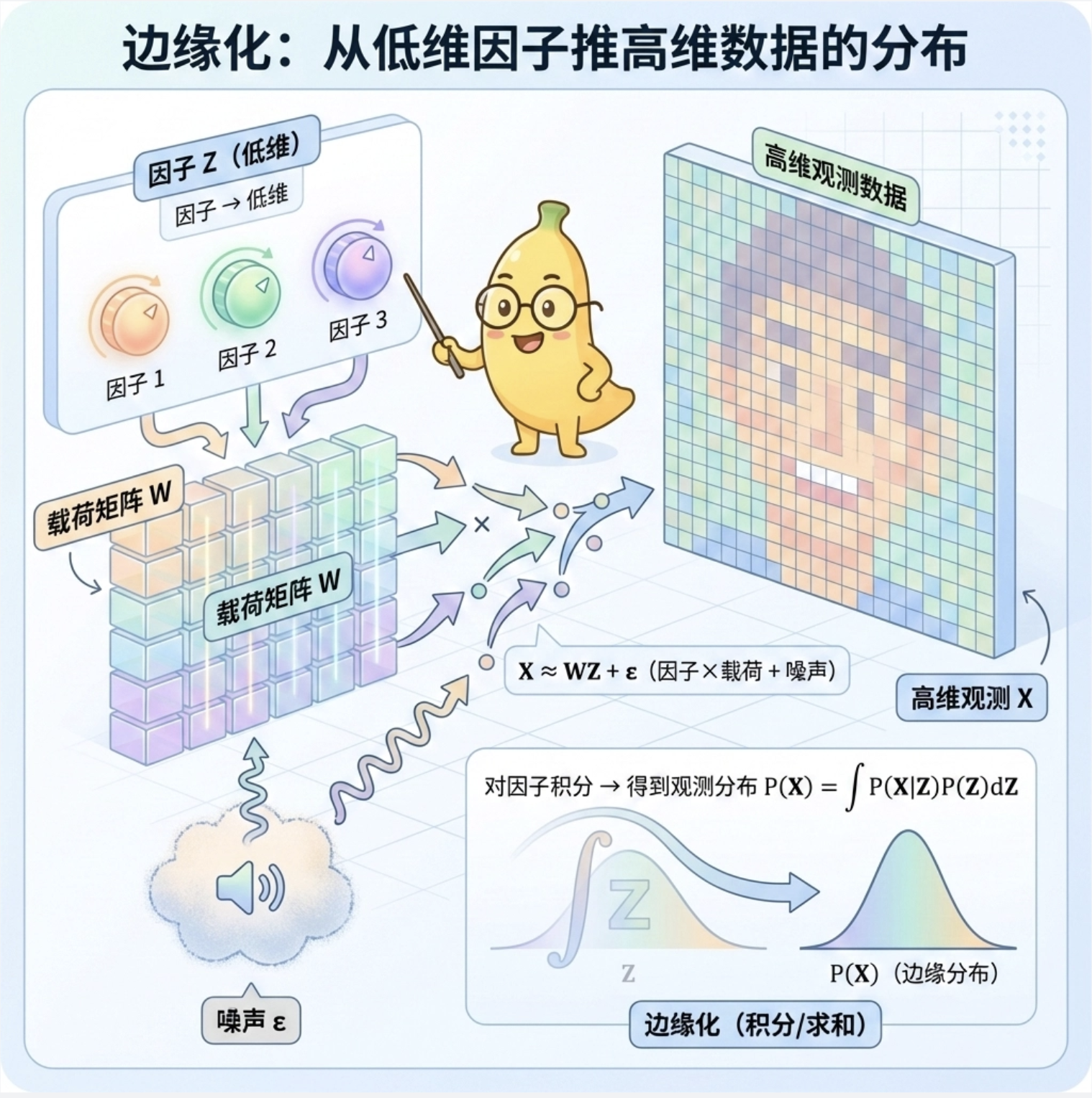
边缘化就是 "从低维因子推高维数据的分布",核心是把高维数据拆成 "因子 × 载荷矩阵 + 噪声"。
7.6.2 因子分析学习的 EM
完整代码 + 可视化(因子分析降维 vs PCA)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FactorAnalysis, PCA
from sklearn.datasets import make_blobs
# ========== Mac配置 ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ========== 生成高维数据(10维→2维) ==========
np.random.seed(42)
# 生成10维数据,3个聚类
X, y = make_blobs(n_samples=500, n_features=10, centers=3, random_state=42)
# ========== 因子分析 vs PCA降维 ==========
# 因子分析(降到2维)
fa = FactorAnalysis(n_components=2, random_state=42)
X_fa = fa.fit_transform(X)
# PCA(降到2维)
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X)
# ========== 可视化对比 ==========
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
# 子图1:因子分析降维结果
ax[0].scatter(X_fa[y==0,0], X_fa[y==0,1], c='skyblue', label='类别0', alpha=0.7)
ax[0].scatter(X_fa[y==1,0], X_fa[y==1,1], c='salmon', label='类别1', alpha=0.7)
ax[0].scatter(X_fa[y==2,0], X_fa[y==2,1], c='lightgreen', label='类别2', alpha=0.7)
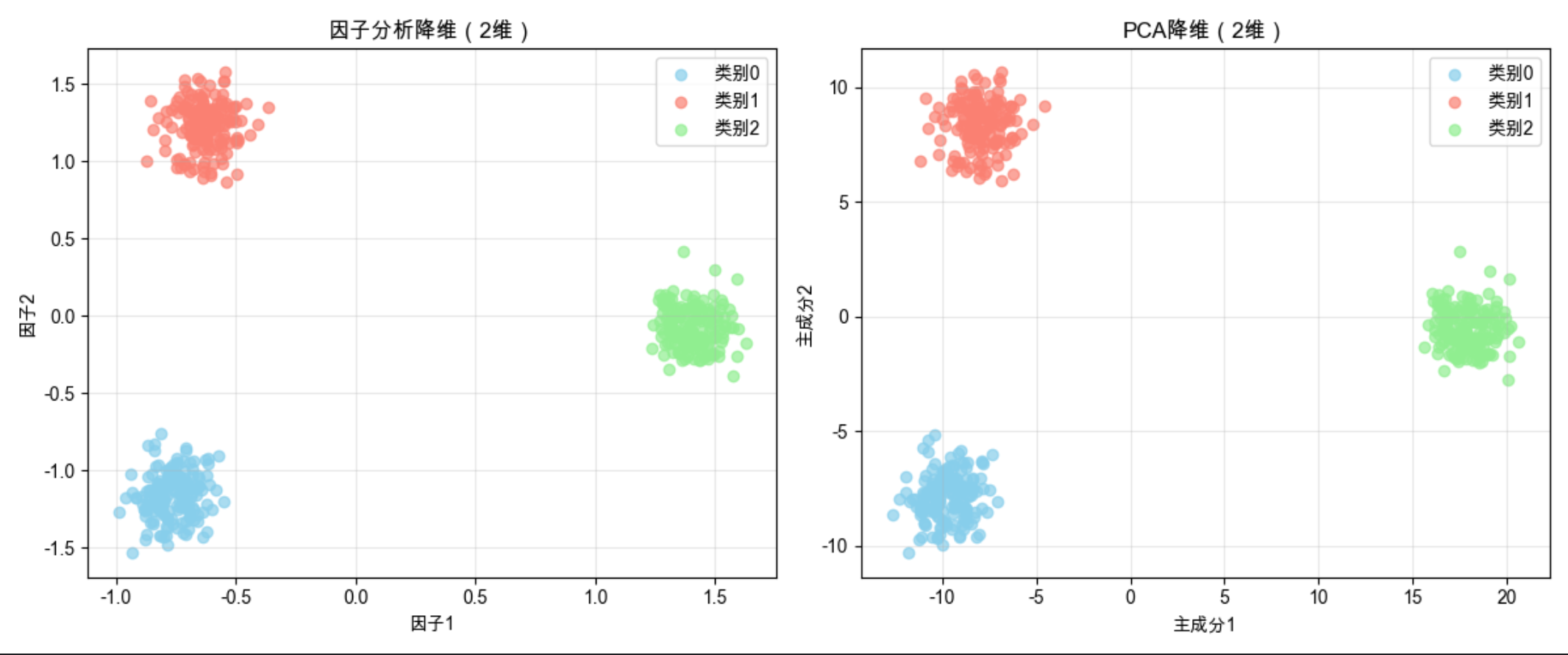
ax[0].set_title('因子分析降维(2维)')
ax[0].set_xlabel('因子1')
ax[0].set_ylabel('因子2')
ax[0].legend()
ax[0].grid(alpha=0.3)
# 子图2:PCA降维结果
ax[1].scatter(X_pca[y==0,0], X_pca[y==0,1], c='skyblue', label='类别0', alpha=0.7)
ax[1].scatter(X_pca[y==1,0], X_pca[y==1,1], c='salmon', label='类别1', alpha=0.7)
ax[1].scatter(X_pca[y==2,0], X_pca[y==2,1], c='lightgreen', label='类别2', alpha=0.7)
ax[1].set_title('PCA降维(2维)')
ax[1].set_xlabel('主成分1')
ax[1].set_ylabel('主成分2')
ax[1].legend()
ax[1].grid(alpha=0.3)
plt.tight_layout()
plt.show()运行效果
7.7 组合模型

核心概念
组合模型是 "把不同模型拼起来用"------ 比如用 GMM 描述人脸的局部特征,用因子分析降维,再用 t 分布处理异常值,形成一个 "混合战队" 解决复杂问题。
通俗比喻

组合模型就像做饭:GMM 是切菜(拆分数据),因子分析是调味(降维提味),t 分布是防糊锅(抗异常),合起来做出一桌好菜。
7.8 期望最大化算法的细节
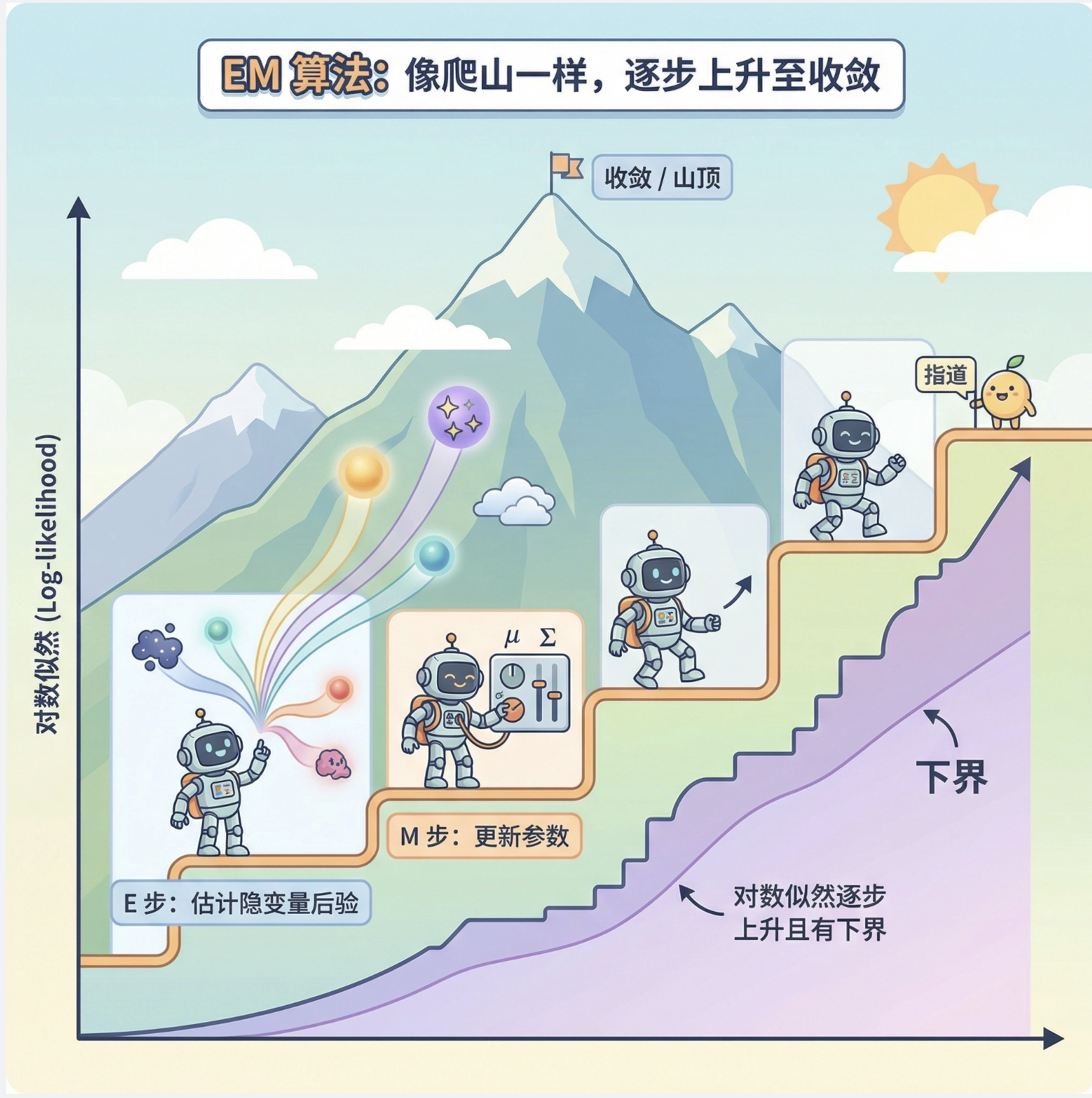
7.8.1 EM 的下界
EM 算法每次迭代都能让模型的 "对数似然" 上升,且有一个下界(不会无限上升),就像爬山,每次都往高处走,直到山顶(收敛)。
7.8.2 E 步
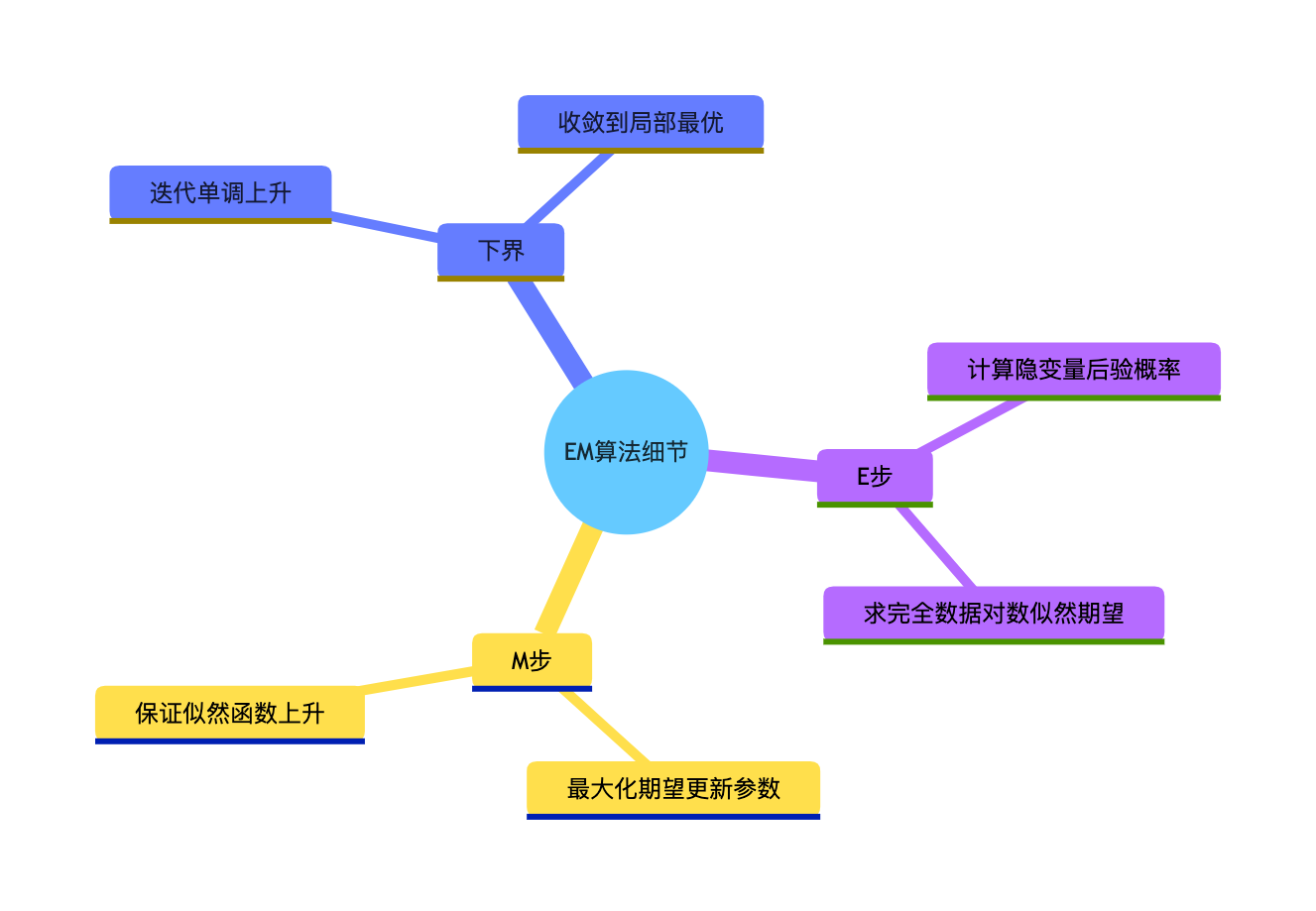
核心:计算 "完全数据的对数似然关于隐变量的期望",简单说就是 "基于当前参数,算隐变量最可能的值"。
7.8.3 M 步
核心:最大化这个期望,更新模型参数,简单说就是 "用隐变量的猜测值,优化模型"。
思维导图
7.9 应用(核心实战)
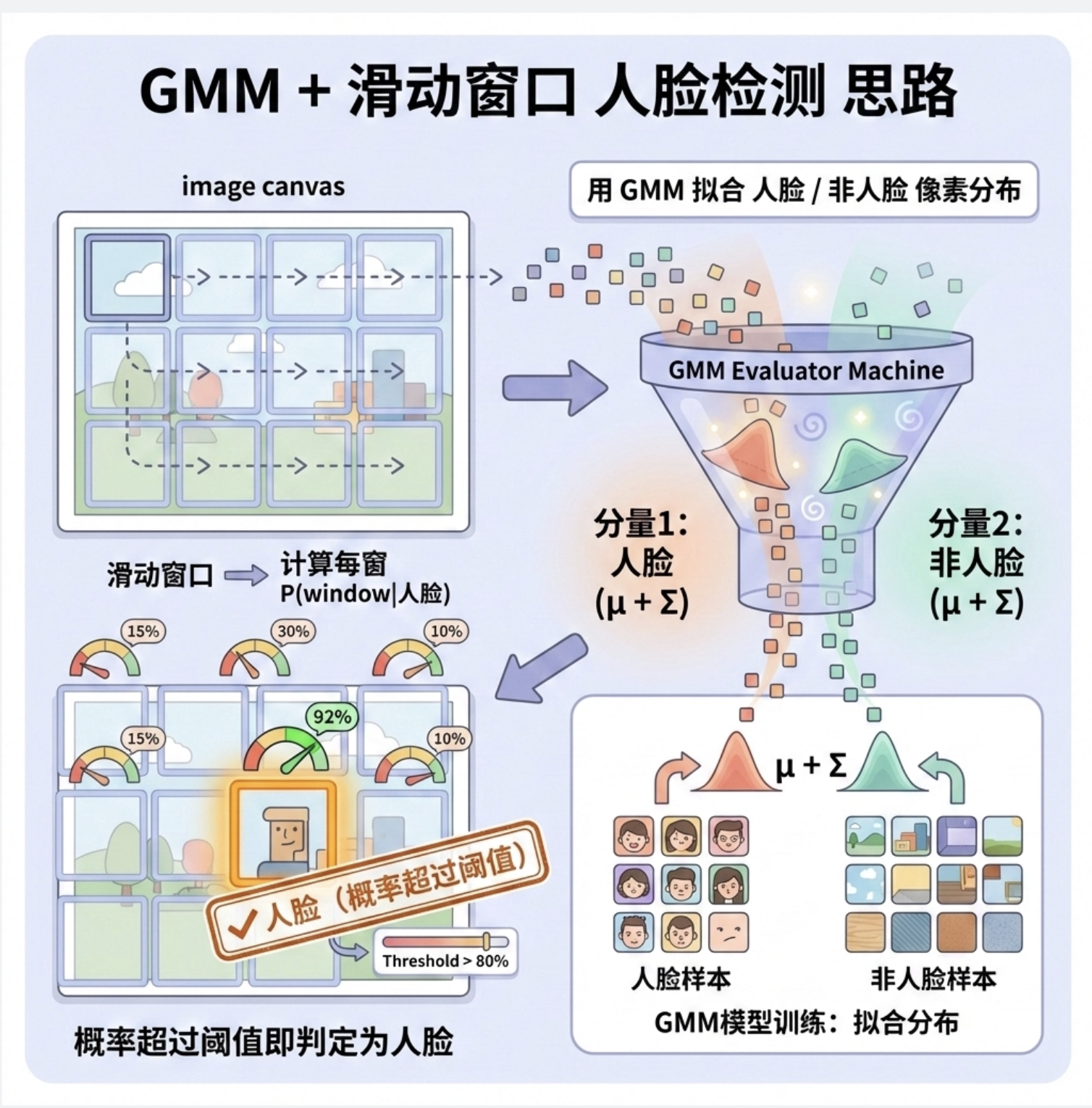
7.9.1 人脸检测
用 GMM 拟合 "人脸" 和 "非人脸" 的像素分布,滑动窗口遍历图像,计算每个窗口属于 "人脸分布" 的概率,概率超过阈值就是人脸。
7.9.2 目标识别
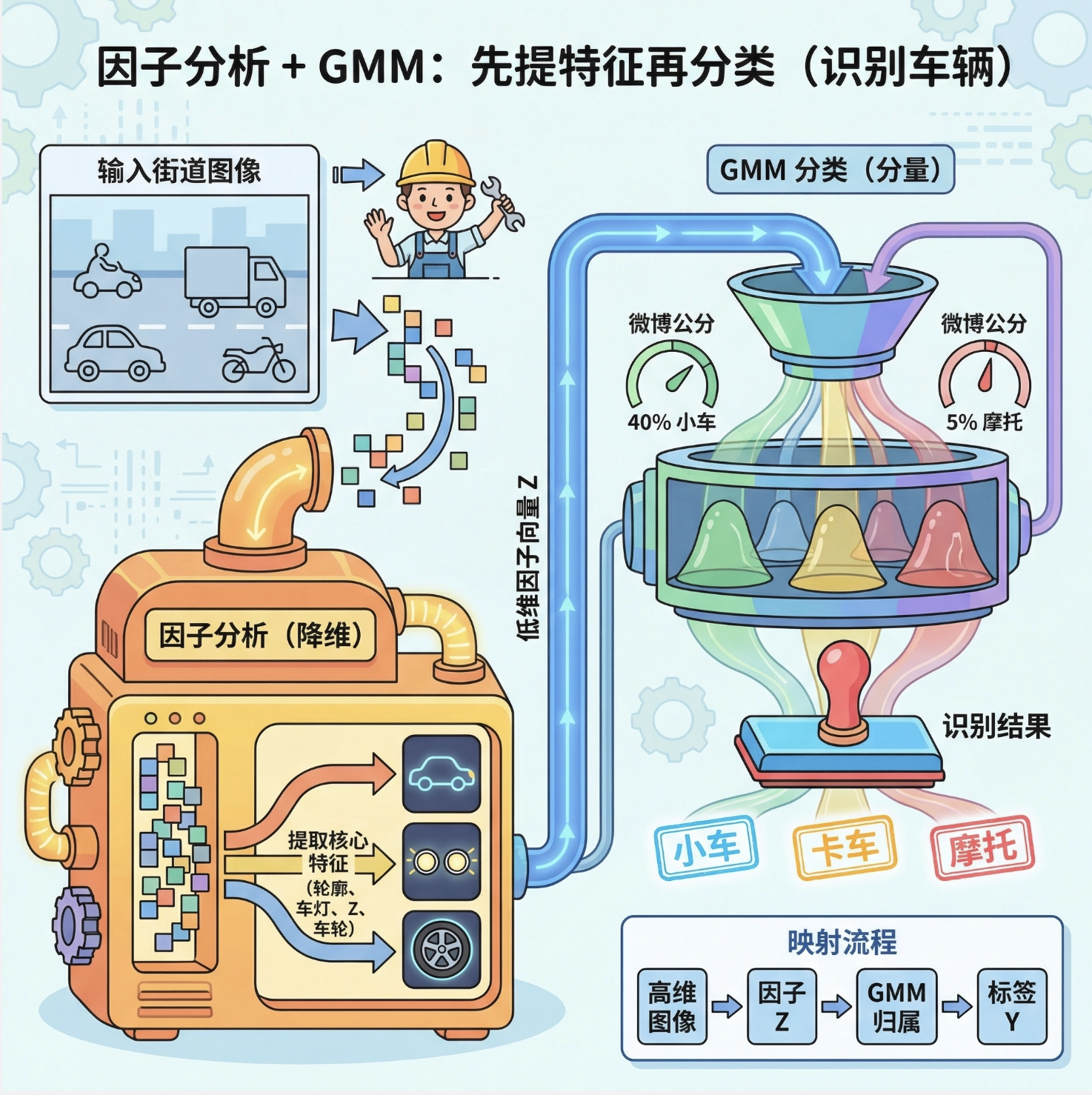
用因子分析提取目标的核心特征(比如汽车的轮廓、车灯位置),再用 GMM 分类,识别不同目标。
7.9.3 分割
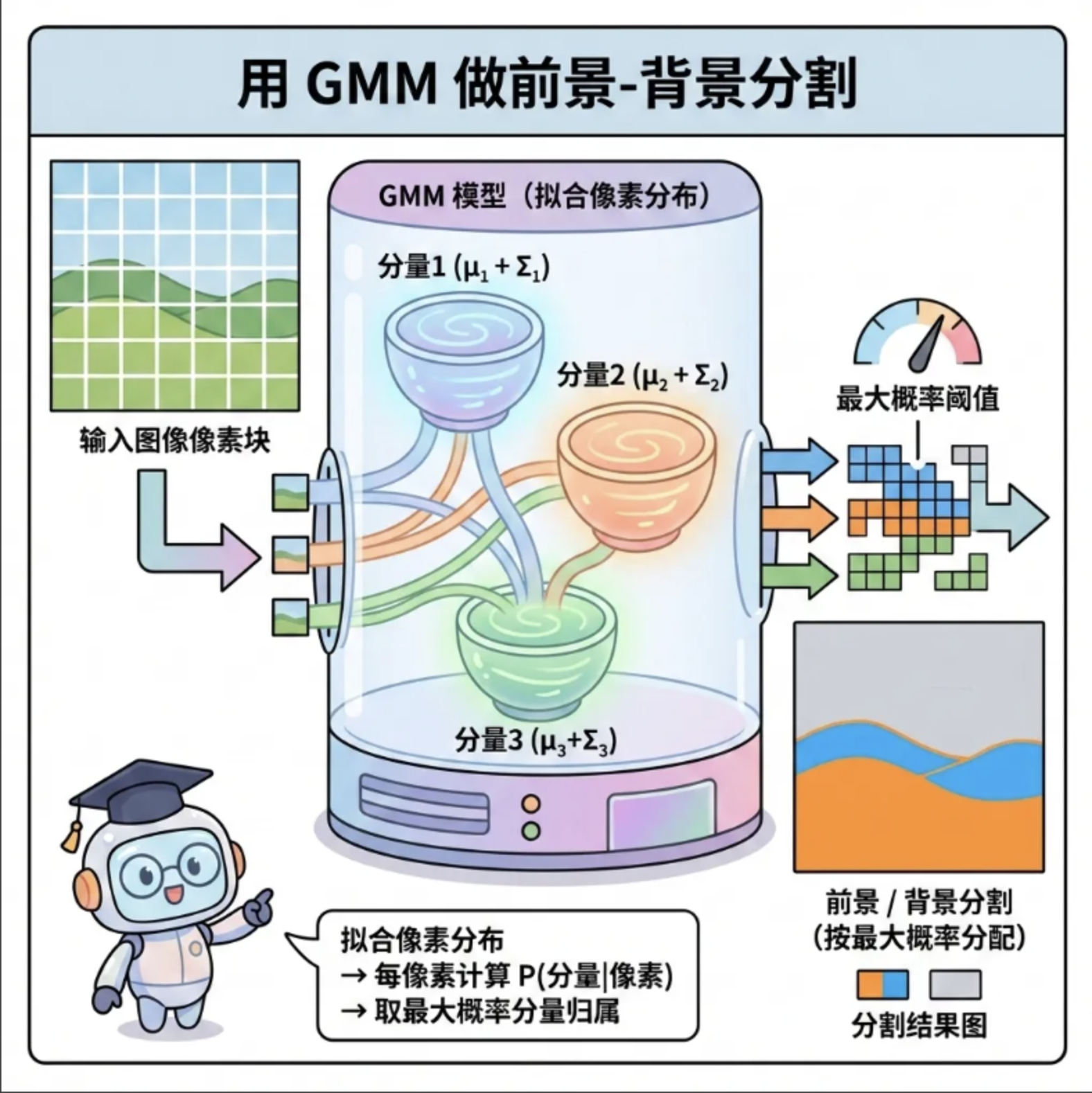
用 GMM 拟合图像的像素分布(比如前景和背景),每个像素分配到概率最大的分量,实现前景 / 背景分割。
分割实战代码 + 可视化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from skimage import io, color
# ========== Mac配置 ==========
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ========== 加载图像(灰度图) ==========
# 替换成你的本地图像路径,或用示例图
img = io.imread('test.jpg', as_gray=True)
# 展平数据(像素点→1维)
X = img.reshape(-1, 1)
# ========== GMM分割(2分量:前景+背景) ==========
gmm = GaussianMixture(n_components=2, random_state=42)
labels = gmm.fit_predict(X)
# 重构分割后的图像
seg_img = labels.reshape(img.shape)
# ========== 可视化对比 ==========
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
# 子图1:原始图像
ax[0].imshow(img, cmap='gray')
ax[0].set_title('原始图像')
ax[0].axis('off')
# 子图2:GMM分割结果
ax[1].imshow(seg_img, cmap='gray')
ax[1].set_title('GMM前景/背景分割')
ax[1].axis('off')
plt.tight_layout()
plt.show()运行效果

7.9.4 正脸识别
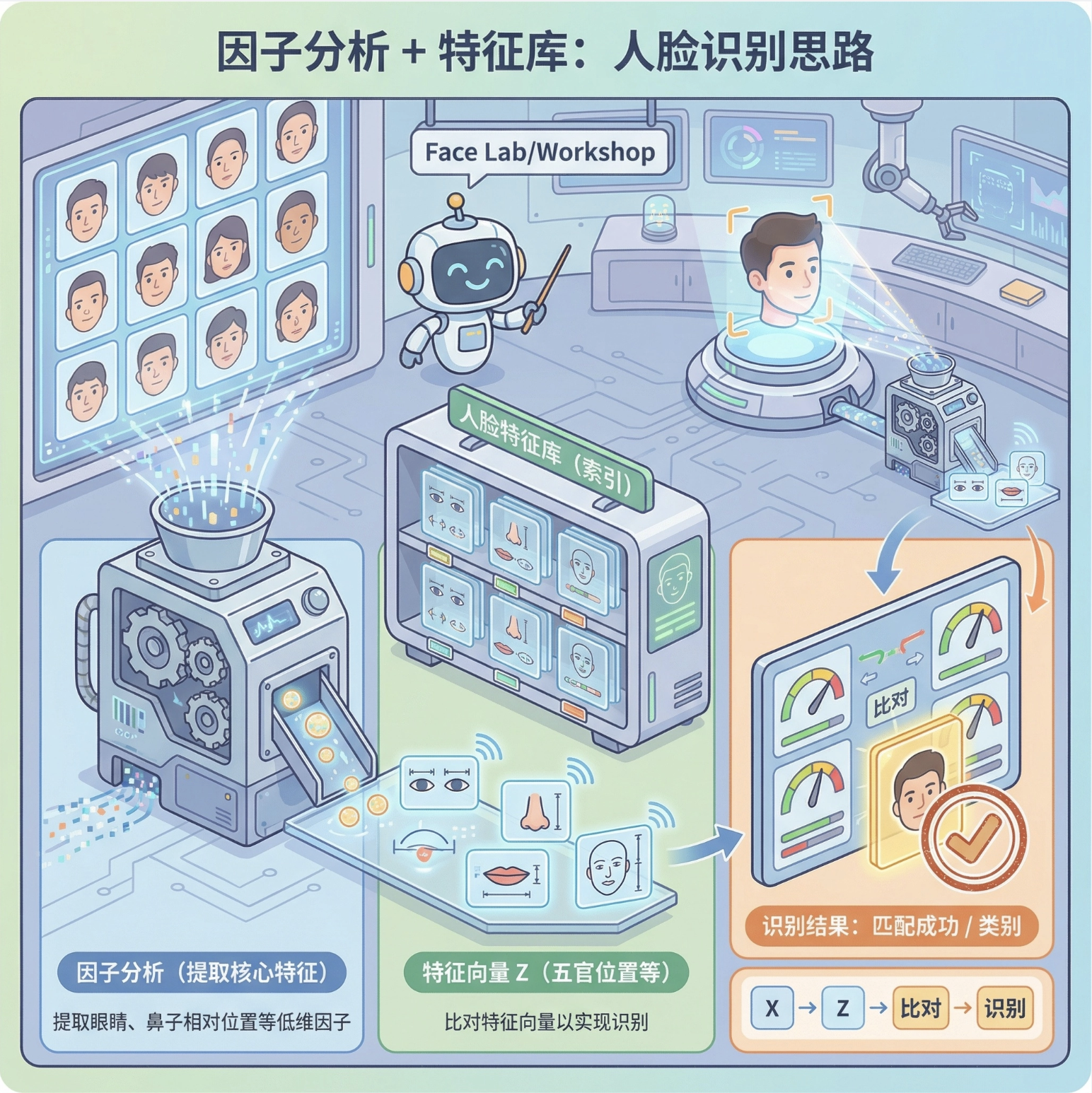
用因子分析提取正脸的核心特征(比如眼睛、鼻子的相对位置),构建 "人脸特征库",新人脸进来后对比特征库,实现识别。
7.9.5 改变人脸姿态(回归)
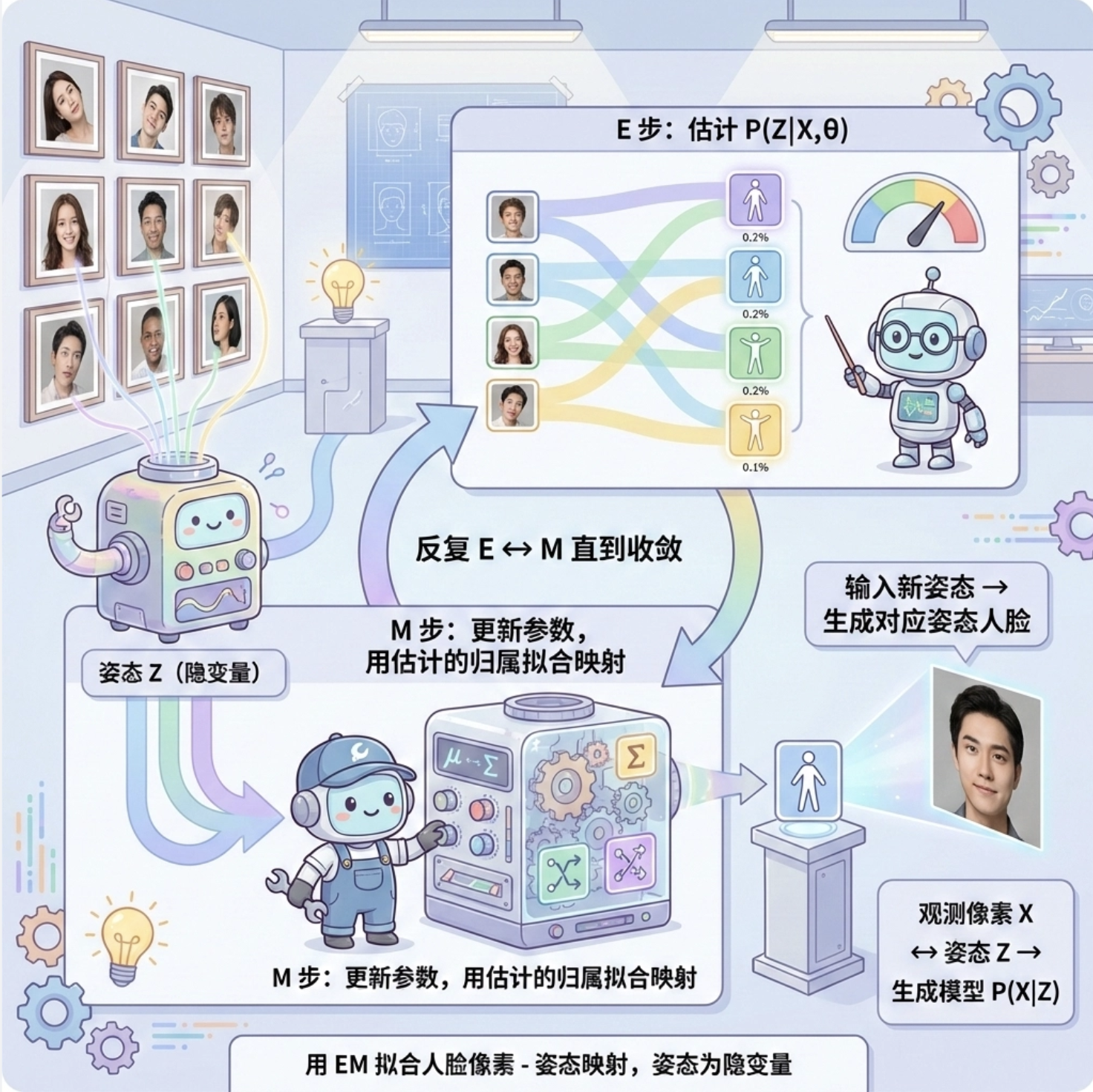
把 "姿态" 作为隐变量,用 EM 算法拟合 "人脸像素 - 姿态" 的映射关系,输入新姿态,生成对应姿态的人脸。
7.9.6 作为隐变量的变换
把图像的变换(旋转、缩放、平移)作为隐变量,用 EM 算法估计这些变换参数,实现图像对齐。
总结
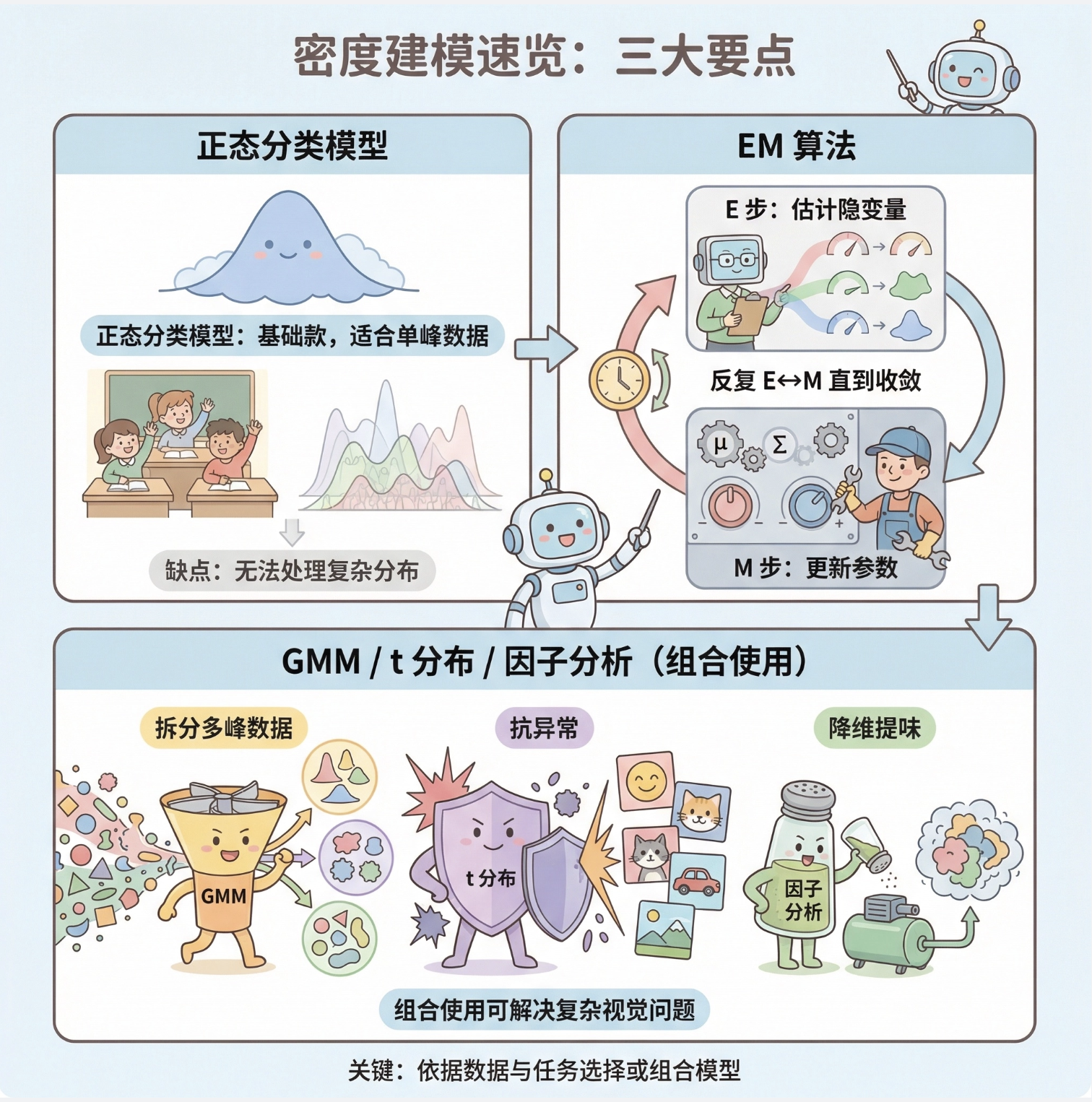
核心知识点
1.正态分类模型 :基础款密度建模,适合单峰数据,缺点是无法处理复杂分布。
2.EM 算法 :处理隐变量的核心工具,E 步猜隐变量,M 步更参数,循环收敛。
3.GMM/t 分布 / 因子分析:GMM 拆分多峰数据,t 分布抗异常,因子分析降维,组合使用可解决复杂计算机视觉问题。
实战要点
1.所有代码均适配 Mac 系统,直接复制即可运行(需安装 numpy/matplotlib/sklearn/scipy)。
2.可视化是理解模型的关键:对比图能直观看到不同模型的优缺点(比如 GMM 比单高斯拟合复杂数据更好)。
3.应用层核心是 "隐变量思维":把看不见的特征 / 状态作为隐变量,用 EM 算法破解复杂问题。
备注
1.代码中用到的第三方库安装命令:pip install numpy matplotlib scikit-learn scipy scikit-image。
2.所有随机种子固定为 42,保证结果可复现。
3.若图像加载失败,替换test.jpg为你的本地图像路径(建议用灰度图测试分割效果)。
习题
1.修改 GMM 代码,尝试 n_components=2/4,观察拟合效果的变化,理解 "分量数" 的选择原则。
2.给 t 分布代码增加更多异常值,调整 df(自由度),观察 df 越小是否抗异常能力越强。
3.用自己的人脸照片(灰度化),运行分割代码,尝试 3 分量 GMM,观察分割效果。