算法—穷举，爆搜，深搜，回溯，剪枝

孞㐑￥2026-02-22 12:06

目录

全排列

子集

找出所有子集的异或总和再求和

[全排列 II](#全排列 II)

电话号码的字母组合​编辑

括号生成​编辑

组合

目标和

组合总和

字母大小写全排列

优美的排列

[N 皇后](#N 皇后)

有效的数独

解数独

单词搜索

黄金矿工

[不同路径 III](#不同路径 III)

全排列

思路：

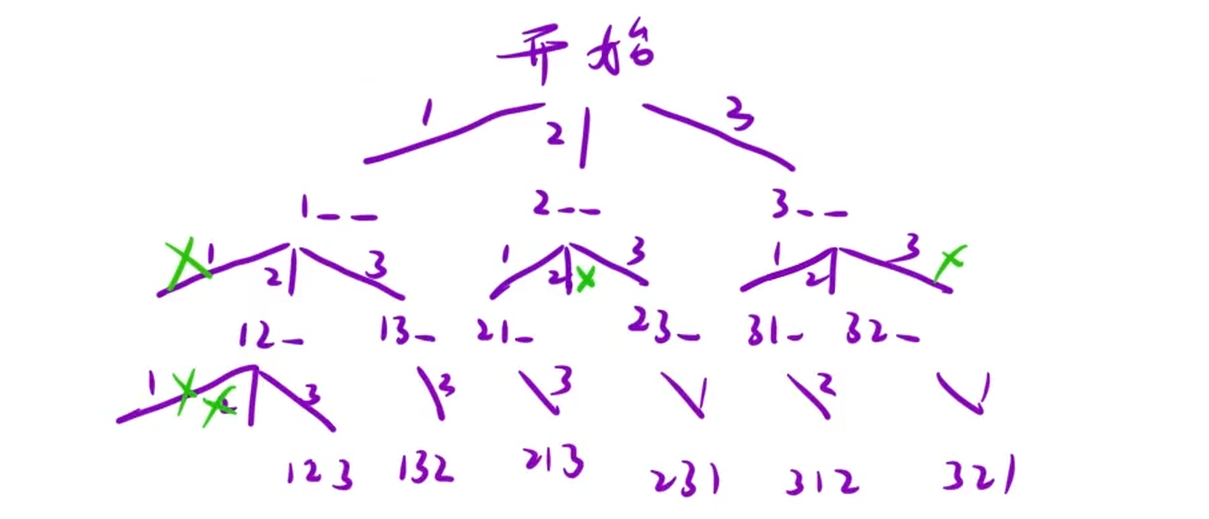
根据上图所画的决策树，我们只需要通过递归，前序遍历这颗决策树，然后把所有的路径都存起来，这些路径其实就是全排列。但是递归的过程中已经选过的数字就不能再选了，所以可以通过一个标记数组来解决这个问题，用它标记哪些数是被选过的，然后遍历数组选数字的时候，选过的数就不选了。另外还需要一个变量记录每条路径，当路径长度和数组元素个数相等，说明这条路径已经到底了（即这条路径结束了），将这个路径放入结果数组中即可。

**细节问题：**回溯的时候（即递归向上返回的时候）需要恢复现场，因为一旦回溯，说明当前这条路径遍历完成了，要开始遍历下一条路径了，那么当前存储路径的这个变量中，属于当前这条路径，但是不属于下一条路径的这些节点都要去除，并且随着这些节点从路径中去除，标记数组也要恢复，因为标记数组标记哪些节点被选了，但是现在这些节点因为回溯回到没有被选的状态，那么标记数组也要恢复。

**恢复有两种方式：**一种是返回上一层之前恢复，这种要找代码中哪里会返回，然后，返回前进行恢复现场；另一种是返回后恢复，这中要找当前代码中递归调用自己的地方，在这个地方下面进行恢复现场（下面代码是返回后恢复的现场）。

代码：

cpp 复制代码 
class Solution 
{
    vector<vector<int>> ret;
    vector<int> path;
    bool check[7];
public:
    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return ret;
    }

    void dfs(vector<int>& nums)
    {
        if(path.size() == nums.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i = 0; i < nums.size(); i++)
        {
            if(check[i] == false)
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums);
                path.pop_back();
                check[i] = false;
            }
        }
    }
};

子集

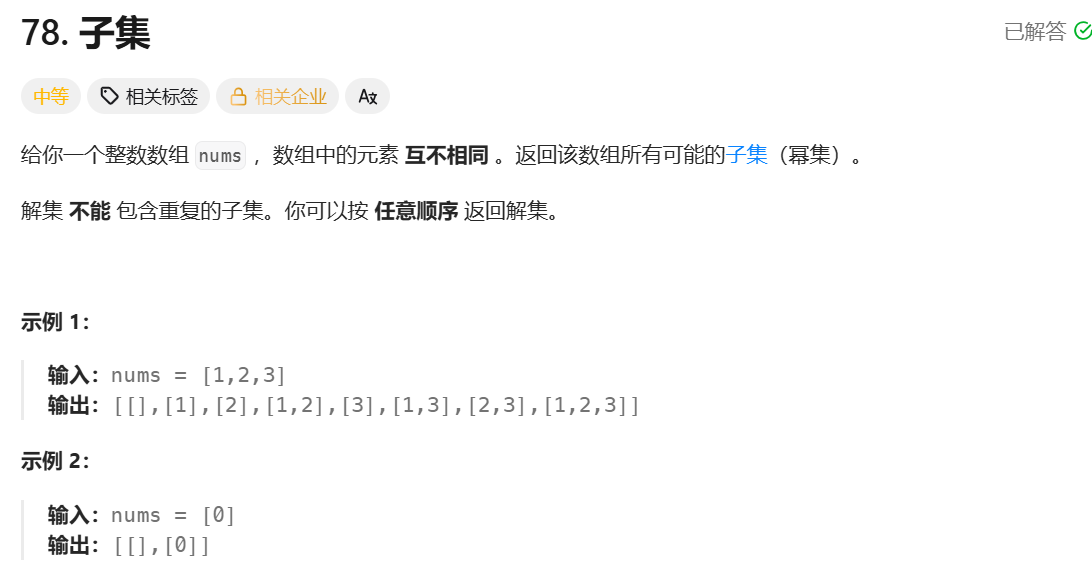
思路：

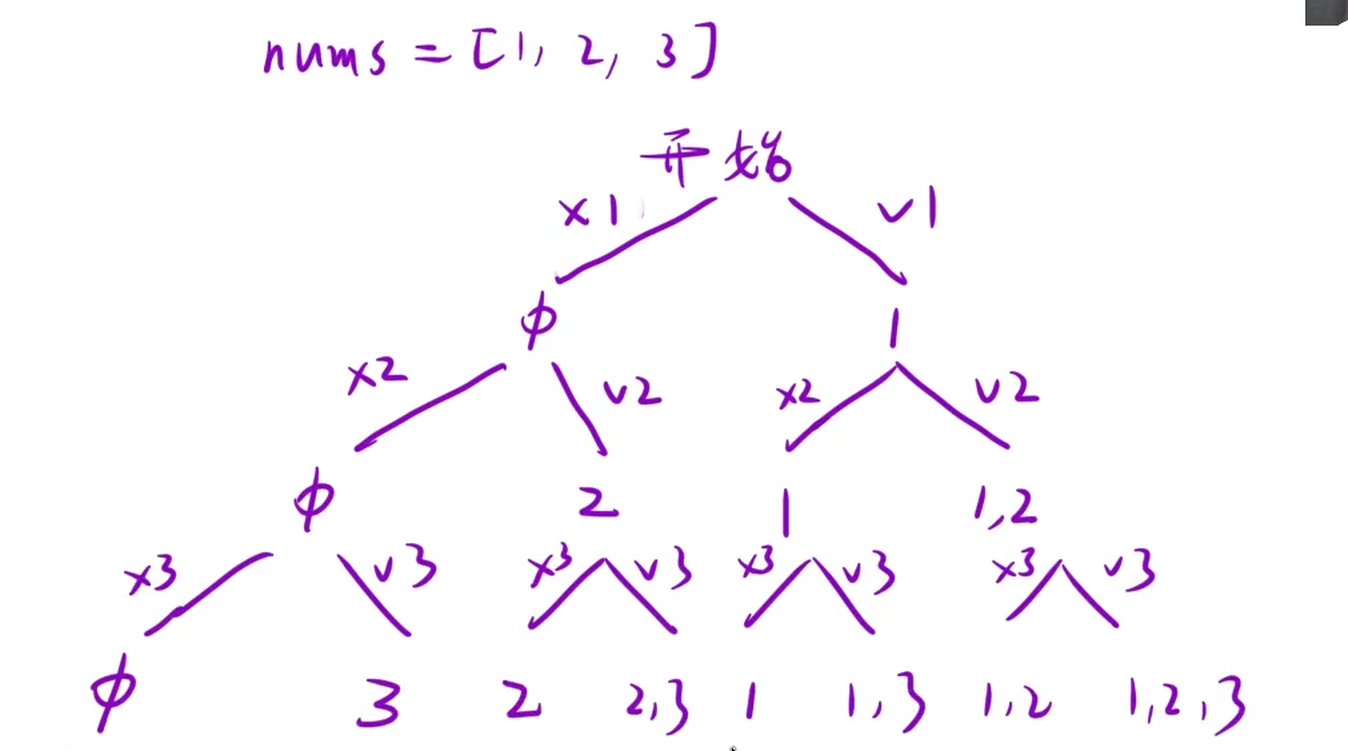
基于当前遍历到的值是选择还是不选择构建一颗决策树，前序遍历这颗数，每条路径就是一个子集，所以递归找到所有路径即可。

代码：

cpp 复制代码 
class Solution 
{
    vector<vector<int>> ret;
    vector<int> path;
public:
    vector<vector<int>> subsets(vector<int>& nums) 
    {
        dfs(nums, 0);
        return ret;
    }

    void dfs(vector<int>& nums, int pos)
    {
        if(pos == nums.size())
        {
            ret.push_back(path);
            return;
        }

        //选择这个值
        path.push_back(nums[pos]);
        dfs(nums, pos + 1);
        path.pop_back();

        //不选这个值
        dfs(nums, pos + 1);
    }
};

找出所有子集的异或总和再求和

思路：

基于当前遍历到的值是选择还是不选择构建一颗决策树，前序遍历这颗数，每条路径就是一个子集，定义一个 path 变量记录路径中所有值的异或结果，然后当一条路径遍历结束后将这个 path 加到总的结果中。

代码：

cpp 复制代码 
class Solution {
    int sum = 0;
    int path = 0;
public:
    int subsetXORSum(vector<int>& nums) {
        dfs(nums, 0);
        return sum;
    }

    void dfs(vector<int>& nums, int pos){
        if(pos == nums.size()){
            sum += path;
            return;
        }

        path ^= nums[pos]; //选择当前这个数
        dfs(nums, pos + 1);
        path ^= nums[pos];  //递归返回到这一层的时候恢复现场

        dfs(nums, pos + 1); //不选择当前这个数
    }
};

全排列 II

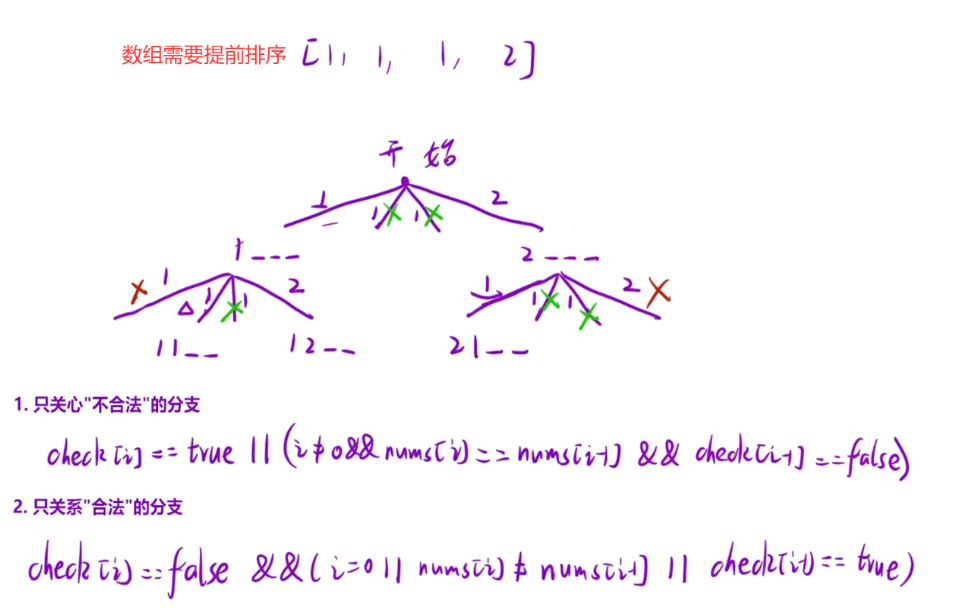
**思路：**剪枝思路如下图

代码：

cpp 复制代码 
class Solution 
{
    vector<vector<int>> ret;
    vector<int> path;
    bool check[8];
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) 
    {
        sort(nums.begin(), nums.end());
        dfs(nums, 0);
        return ret;
    }

    void dfs(vector<int>& nums, int pos)
    {
        if(pos == nums.size())
        {
            ret.push_back(path);
            return;
        }

        for(int i = 0; i < nums.size(); i++)
        {
            if(check[i] == false && (i == 0 || nums[i] != nums[i - 1] || check[i - 1] == true))
            {
                path.push_back(nums[i]);
                check[i] = true;
                dfs(nums, pos + 1);
                check[i] = false;
                path.pop_back();
            }
        }
    }
};

电话号码的字母组合

思路：

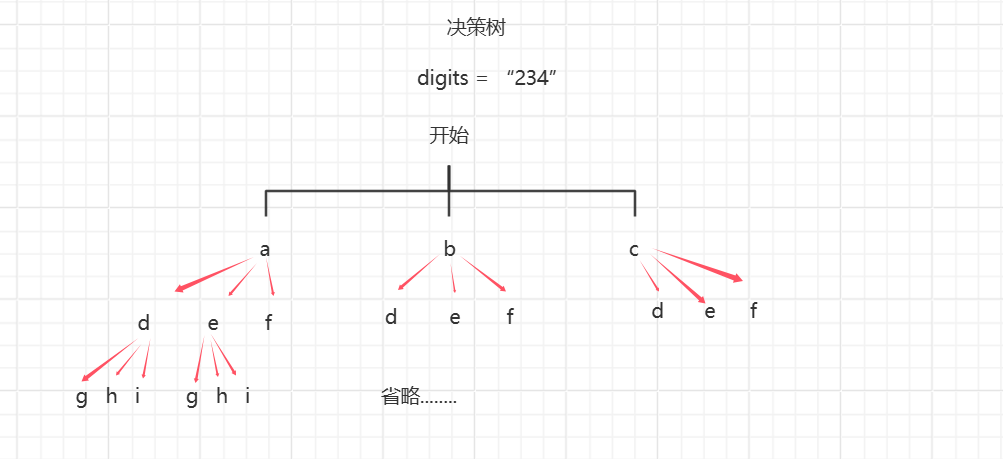
通过哈希将数字和字符串映射起来，然后结合上图决策树，递归遍历每条路径，所有路径合起来就是所有的字母组合。

**为什么不需要标记数组表示当前值有没有被选过：**全排列那道题需要标记数组表示当前值有没有被选过，选过就不能选了，那是因为那道题是针对一组元素进行排列，如下图：

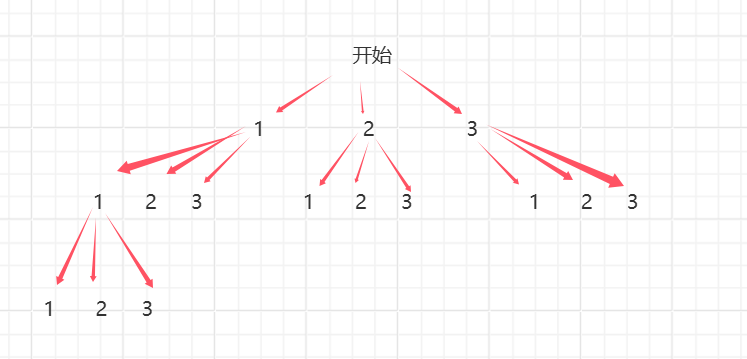
第二层的 1 和第一层是同一个数，第一轮已经选过了，所以不能选，需要标记数组标记一下，防止选重复。但是这道题每层的值和上一层的值都没有关系，都是一组新的元素，即使可能是重复的，比如 digits 是 "222" 的情况下，但是这是三组元素，它们各自独立，可以重复选，所以不需要这个标记数组。

代码：

cpp 复制代码 
class Solution {
    vector<string> ret;
    string path;
    string hash[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
public:
    vector<string> letterCombinations(string digits) {
        if(digits.size() == 0)
            return ret;
        dfs(digits, 0);
        return ret;
    }

    void dfs(string& digits, int n){
        if(path.size() == digits.size()){
            ret.push_back(path);
            return;
        }

        for(auto ch : hash[digits[n] - '0']){
            path.push_back(ch);
            dfs(digits, n + 1);
            path.pop_back();
        }
    }
};

括号生成

思路：

有效的括号组合的条件：

  1. 左括号的数量 = 右括号的数量
  2. 从头开始的任意一个子串，左括号的数量 >= 右括号的数量

决策树：

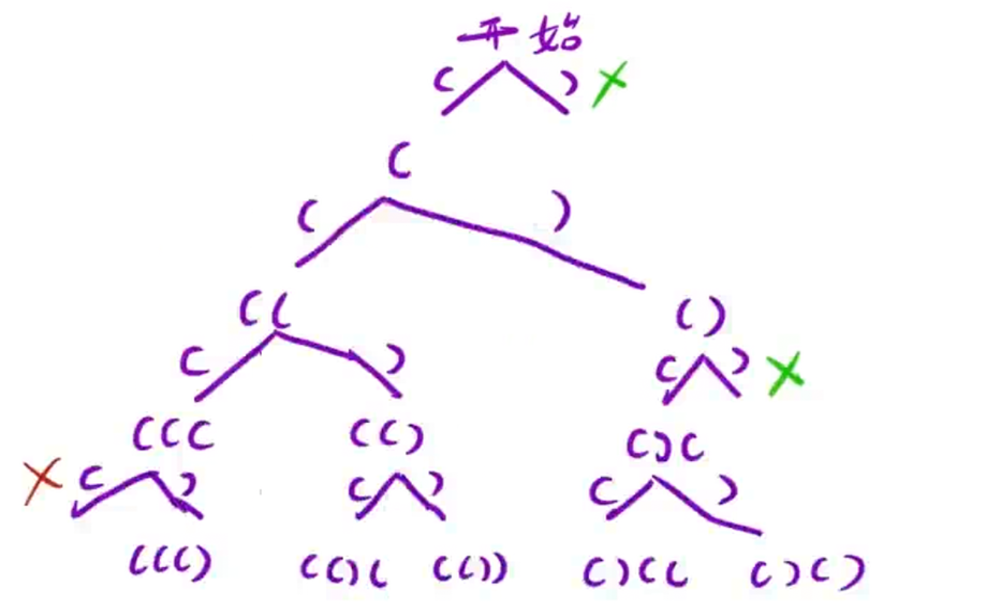
代码：

cpp 复制代码 
class Solution {
    int left, right, _n;
    string path;
    vector<string> ret;
public:
    vector<string> generateParenthesis(int n) {
        left = right = 0;
        _n = n;
        dfs();
        return ret;
    }

    void dfs(){
        if(right == _n){
            ret.push_back(path);
            return;
        }

        if(left < _n){
            path.push_back('(');
            left++;
            dfs();
            path.pop_back();
            left--;
        }

        if(right < left){
            path.push_back(')');
            right++;
            dfs();
            path.pop_back();
            right--;
        }
    }
};

组合

思路：

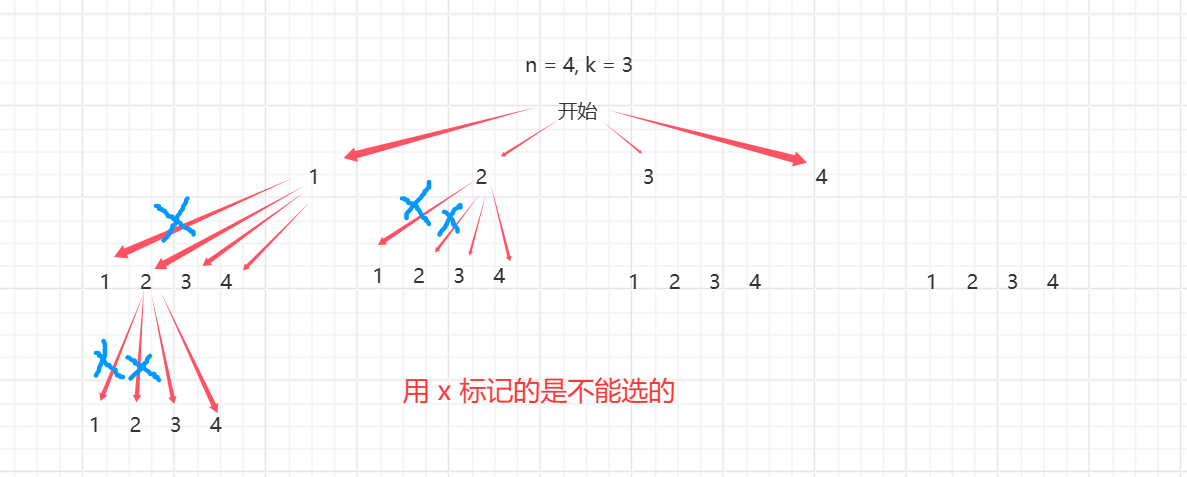
代码：

cpp 复制代码 
class Solution {
    int _n, _k;
    vector<vector<int>> ret;
    vector<int> path;
public:
    vector<vector<int>> combine(int n, int k) {
        _n = n;
        _k = k;
        dfs(1);
        return ret;
    }

    void dfs(int num){
        if(path.size() == _k){
            ret.push_back(path);
            return;
        }

        for(int i = num; i <= _n; i++){
            path.push_back(i);
            dfs(i + 1);
            path.pop_back();
        }
    }
};

目标和

**思路：**决策树如下

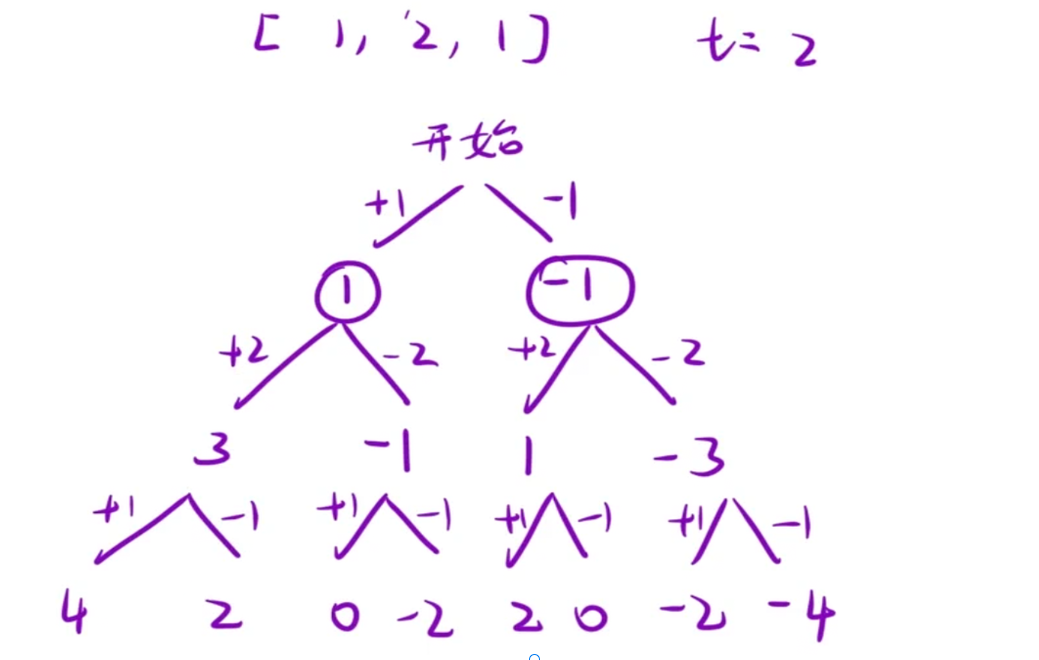
代码：

cpp 复制代码 
class Solution 
{
    int ret, aim;
public:
    int findTargetSumWays(vector<int>& nums, int target) 
    {
        aim = target;
        dfs(nums, 0, 0);
        return ret;    
    }

    void dfs(vector<int>& nums, int pos, int path)
    {
        if(pos == nums.size())
        {
            if(path == aim) ret++;
            return;
        }

        dfs(nums, pos + 1, path + nums[pos]);
        dfs(nums, pos + 1, path - nums[pos]);
    }
};

组合总和

**思路：**决策树如下

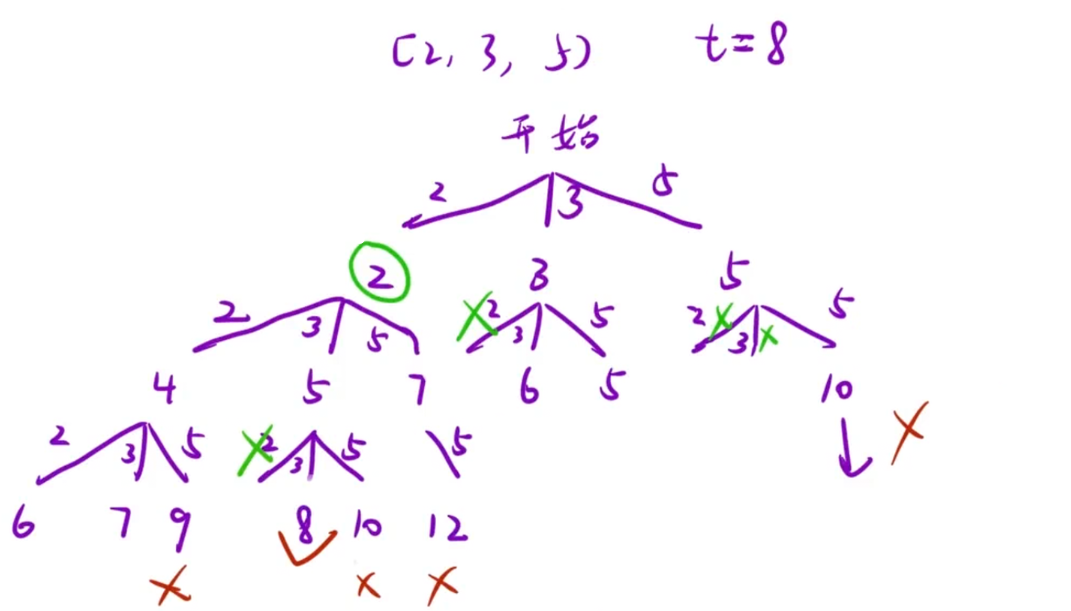
代码：

cpp 复制代码 
class Solution {
    vector<vector<int>> ret;
    vector<int> path;
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        dfs(candidates, target, 0, 0);
        return ret;
    }

    void dfs(vector<int>& candidates, int target, int sum, int n){
        if(sum >= target){
            if(sum == target){
                ret.push_back(path);
            }
            return;
        }

        for(int i = n; i < candidates.size(); i++){
            path.push_back(candidates[i]);
            dfs(candidates, target, sum + candidates[i], i);
            path.pop_back();
        }
    }
};

字母大小写全排列

思路：

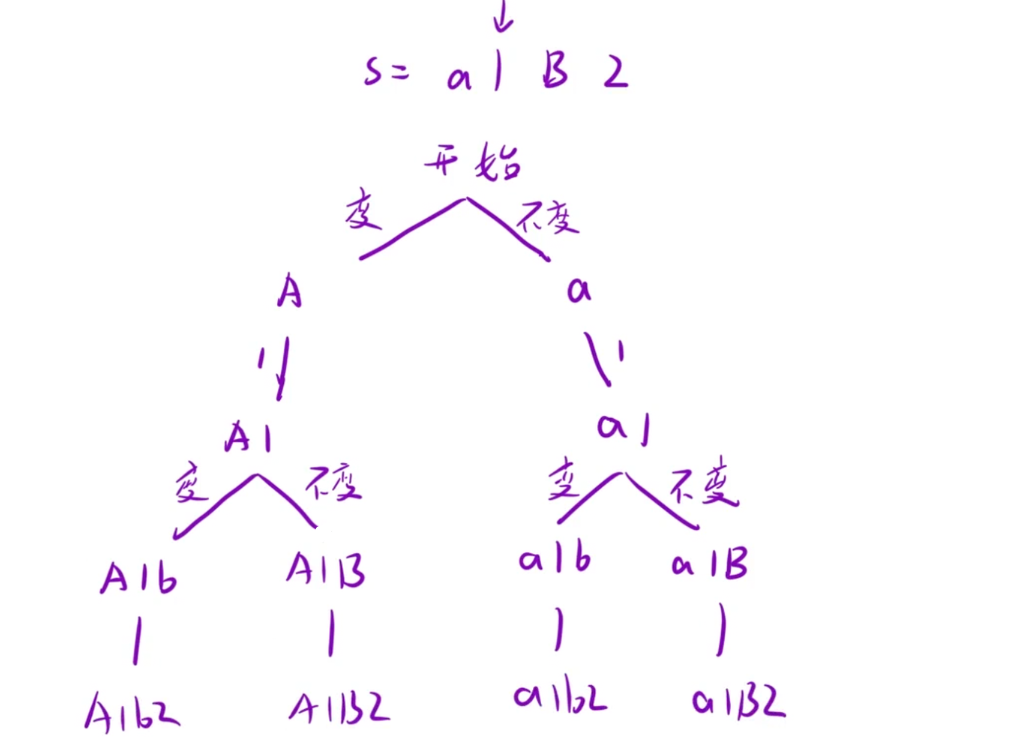
因为只有字母才涉及到变化，数字恒定不变，所以判断是否要变化的时候只需要判断字母即可。

代码：

cpp 复制代码 
class Solution 
{
    vector<string> ret;
    string path;
public:
    vector<string> letterCasePermutation(string s) 
    {
        dfs(s, 0);
        return ret;
    }

    void dfs(string& s, int pos)
    {
        if(path.size() == s.size())
        {
            ret.push_back(path);
            return;
        }

        //大写变小写，小写变大写
        if(s[pos] >= 'a' && s[pos] <= 'z')
        {
            path.push_back(s[pos] - 32);
            dfs(s, pos + 1);
            path.pop_back();
        }
        else if(s[pos] >= 'A' && s[pos] <= 'Z')
        {
            path.push_back(s[pos] + 32);
            dfs(s, pos + 1);
            path.pop_back();            
        }
        
        //不变化
        path.push_back(s[pos]);
        dfs(s, pos + 1);
        path.pop_back();
    }
};

优美的排列

思路：

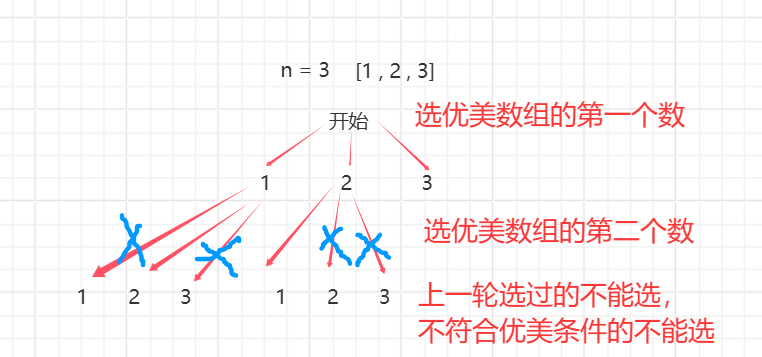
代码：

cpp 复制代码 
class Solution {
    int ret = 0;
    bool check[15];
public:
    int countArrangement(int n) {
        dfs(n, 1);
        return ret;
    }

    void dfs(int n, int k){
        if(k == n + 1){
            ret++;
            return;
        }

        for(int i = 1; i <= n; i++){
            if(check[i] == false && (i % k == 0 || k % i == 0)){
                check[i] = true;
                dfs(n, k + 1);
                check[i] = false;
            }
        }
    }
};

N 皇后

思路：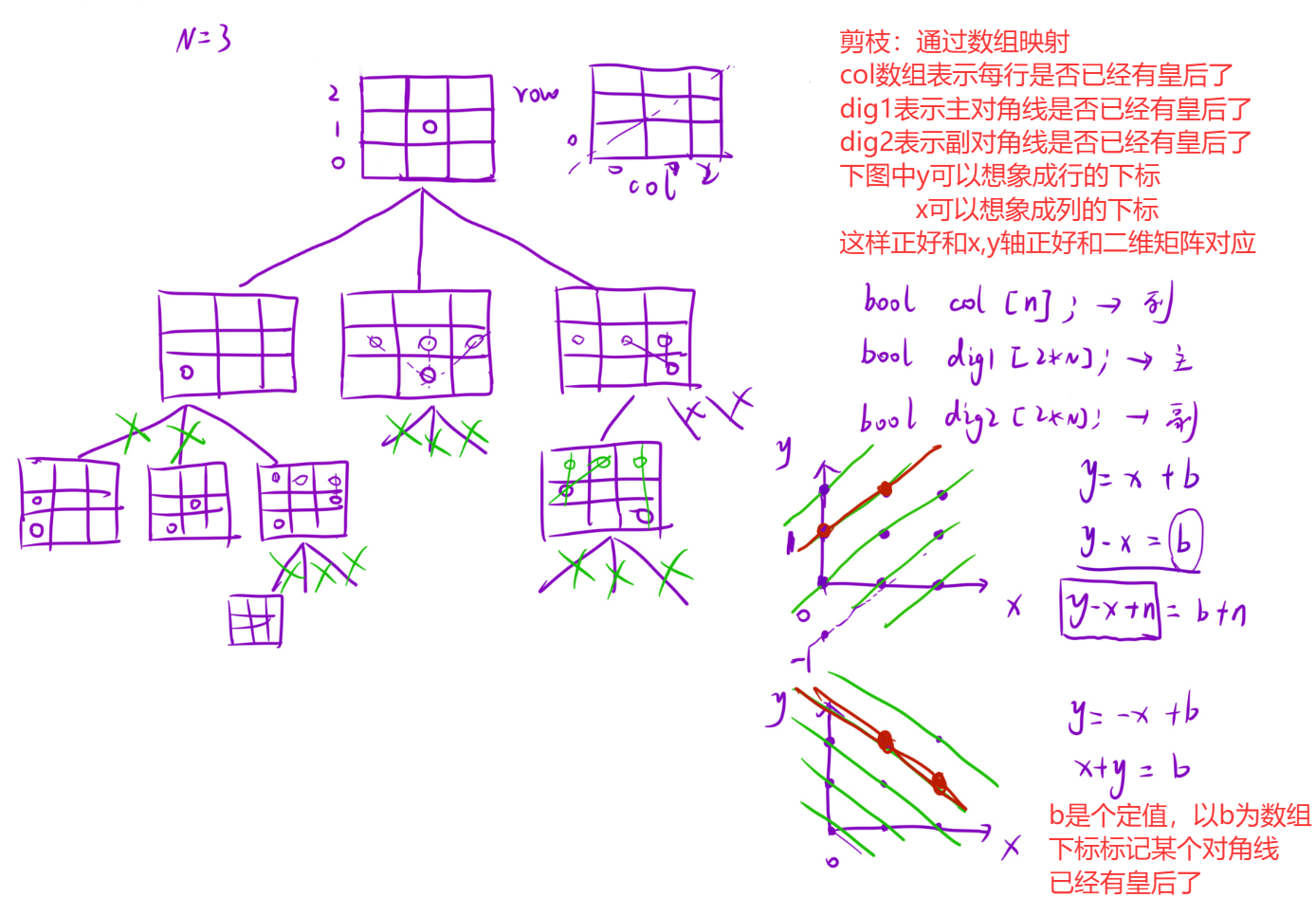

代码：

cpp 复制代码 
class Solution 
{
    vector<vector<string>> ret;
    vector<string> path;
    bool checkCol[10];
    bool checkDig1[20];
    bool checkDig2[20];
    int n;

public:
    vector<vector<string>> solveNQueens(int _n) 
    {
        n = _n;
        path.resize(n);
        for(int i = 0; i < n; i++)
        {
            path[i].append(n, '.');
        }
        dfs(0);
        return ret;
    }

    void dfs(int row)
    {
        if(row == n)
        {
            ret.push_back(path);
            return;
        }

        for(int col = 0; col < n; col++)
        {
            if(!checkCol[col] && !checkDig1[col - row + n] && !checkDig2[col + row])
            {
                path[row][col] = 'Q';
                checkCol[col] = checkDig1[col - row + n] = checkDig2[col + row] = true;
                dfs(row + 1);
                path[row][col] = '.';
                checkCol[col] = checkDig1[col - row + n] = checkDig2[col + row] = false;
            }
        }
    }
};

有效的数独

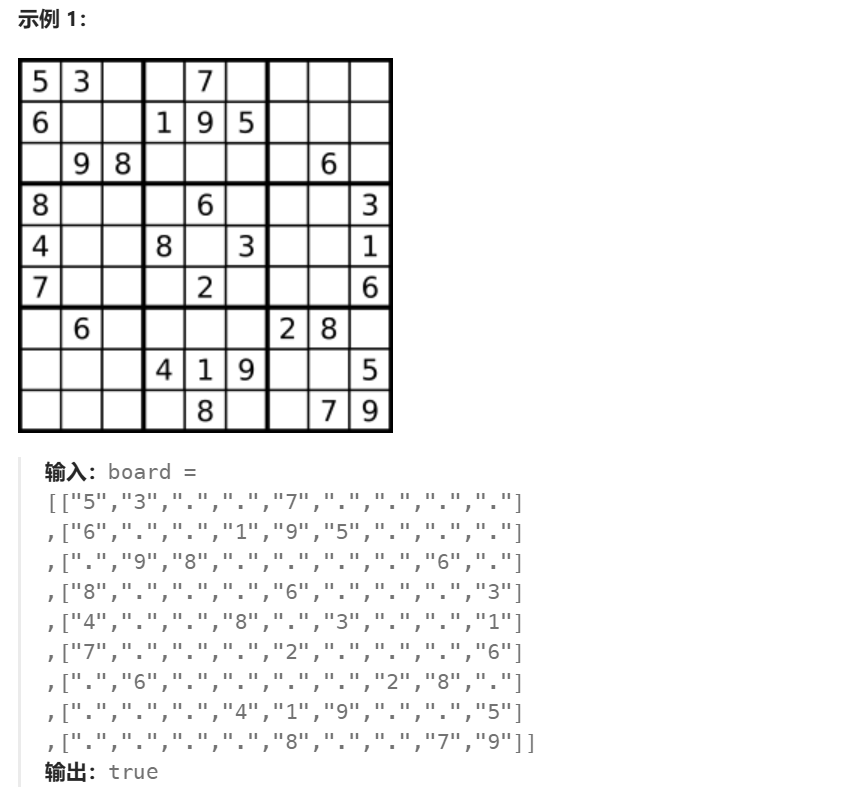
**思路：**创建三个布尔数组

  • bool row[ 9 ][ 10 ]：row[i][j] 表示第 i 行，是否存在 j 这个数，如果存在就是 true。
  • bool col[ 9 ][ 10 ]：col[i][j] 表示第 i 列，是否存在 j 这个数，如果存在就是 true。
  • bool grid[ 3 ][ 3 ][ 10 ]：将原有的9x9的方格看做9个3x3的大格子，grid[i][j][k] 表示下标为 i，j 的格子是否存在 k 这个数，如果存在就是 true。

代码：

cpp 复制代码 
class Solution {
    bool row[9][10];
    bool col[9][10];
    bool grid[3][3][10];
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        for(int i = 0; i < 9; i++){
            for(int j = 0; j < 9; j++){
                if(board[i][j] != '.'){
                    int num = board[i][j] - '0';
                    if(row[i][num] || col[j][num] || grid[i / 3][j / 3][num])
                        return false;
                    row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                }
            }
        }

        return true;
    }
};

解数独

思路：

创建三个布尔数组

  • bool row[ 9 ][ 10 ]：row[i][j] 表示第 i 行，是否存在 j 这个数，如果存在就是 true。
  • bool col[ 9 ][ 10 ]：col[i][j] 表示第 i 列，是否存在 j 这个数，如果存在就是 true。
  • bool grid[ 3 ][ 3 ][ 10 ]：将原有的9x9的方格看做9个3x3的大格子，grid[i][j][k] 表示下标为 i，j 的格子是否存在 k 这个数，如果存在就是 true。

通过上述三个数组标记哪些数字在当前位置不能使用，然后递归遍历二维矩阵中每个没有数字的位置，依次尝试 1 ~ 9，递归函数设计一个返回值，这样我们就可以根据返回值知道这个位置放置的这个数可不可以，如果返回的是 true，表明当前放置的数有最终结果，直接返回true（并且在递归过程中已经完成了每个位置的数字的填充）；如果返回的是 false，直接恢复现场，然后尝试下一个数即可。如果一个位置所有数都不能放，就返回 false。

代码：

cpp 复制代码 
class Solution 
{
    bool row[9][10];
    bool col[9][10];
    bool grid[3][3][10];
public:
    void solveSudoku(vector<vector<char>>& board) 
    {
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] != '.')
                {
                    int num = board[i][j] - '0';
                    row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                }
            }
        }        
        dfs(board);
    }

    bool dfs(vector<vector<char>>& board)
    {
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] == '.')
                {
                    for(int num = 1; num <= 9; num++)
                    {
                        if(!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num])
                        {
                            board[i][j] = '0' + num;
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                            if(dfs(board)) return true;
                            board[i][j] = '.';
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = false;
                        }
                    }
                    return false;
                }
            }
        }
        return true;
    }
};

单词搜索

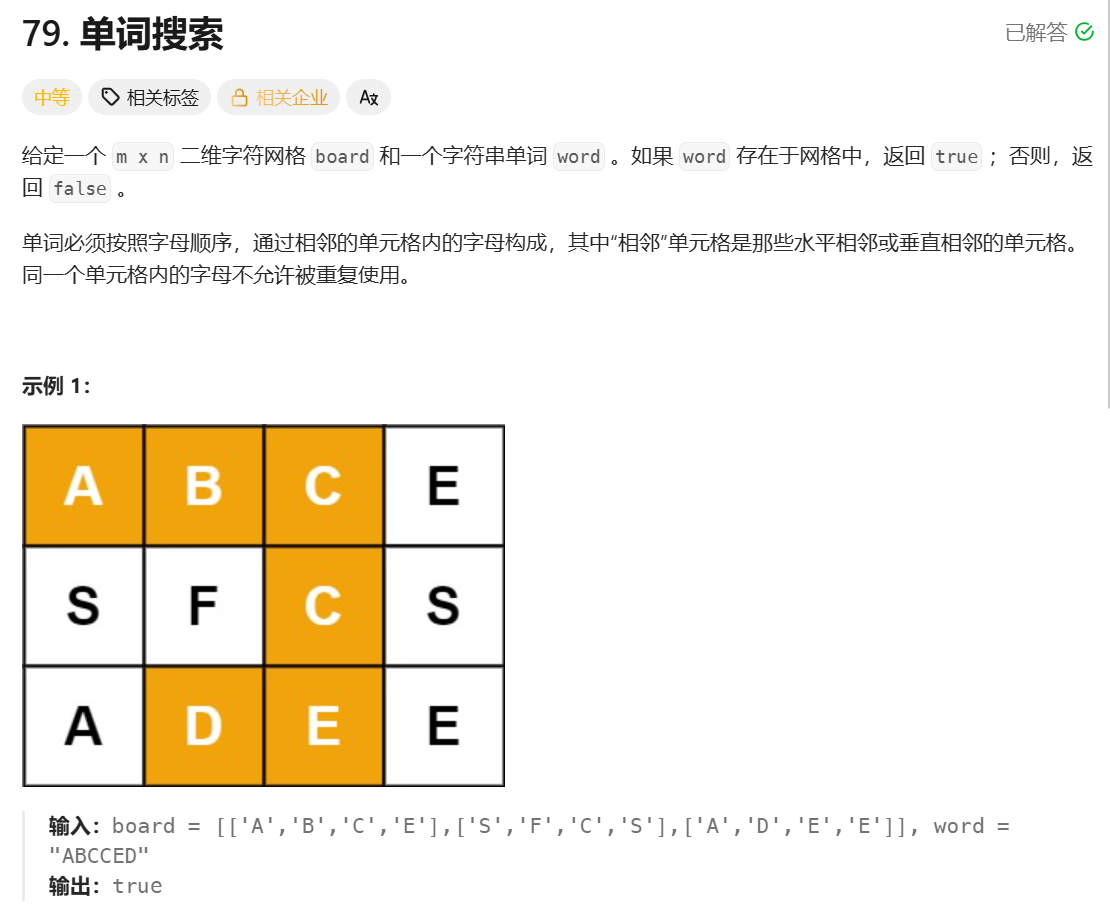
思路：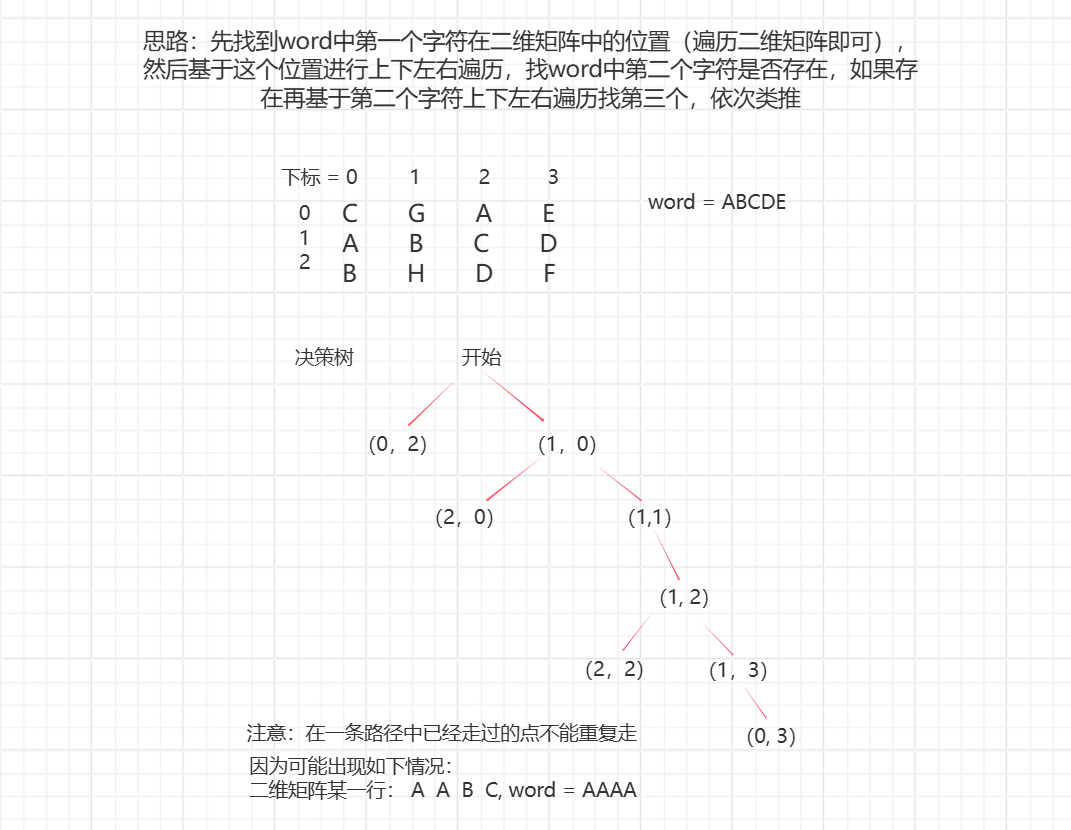

代码：

cpp 复制代码 
class Solution {
    bool vis[7][7];
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int m;
    int n;
public:
    bool exist(vector<vector<char>>& board, string word) {
        m = board.size();
        n = board[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(board[i][j] == word[0])
                {
                    vis[i][j] = true;
                    if(dfs(board, i, j, word, 1)) return true;
                    vis[i][j] = false;
                }
            }
        }

        return false;
    }

    bool dfs(vector<vector<char>>& board, int i, int j, string& word, int pos)
    {
        if(pos == word.size())
            return true;

        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && board[x][y] == word[pos])
            {
                vis[x][y] = true;
                if(dfs(board, x, y, word, pos + 1))
                    return true;
                vis[x][y] = false;
            }
        }

        return false;
    } 
};

黄金矿工

**思路：**遍历二维数组，找到不为 0 的数，然后遍历这个数上下左右四个位置，找到不为 0 且当前这条路径中没有走过的数，然后基于这个数继续上下左右遍历，当遍历到某个位置，它的上下左右四个位置都不合法（值为 0，下标越界，已经访问过了都是非法情况），此时说明这条路径走到底了，更新结果。这里 dfs 方法中 temp 参数是上一轮路径中所有值的总和，不包含 grid[i][j]，所以更新结果的时候要把 grid[i][j] 加上。

代码：

cpp 复制代码 
class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int m;
    int n;
    bool vis[15][15];
    int ret = 0;
public:
    int getMaximumGold(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] != 0)
                {
                    vis[i][j] = true;
                    dfs(grid, i, j, 0);
                    vis[i][j] = false;
                }
            }
        }

        return ret;
    }

    void dfs(vector<vector<int>>& grid, int i, int j, int temp)
    {
        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != 0)
            {
                vis[x][y] = true;
                dfs(grid, x, y, temp + grid[i][j]);
                vis[x][y] = false;
            }
        }

        ret = max(ret, temp + grid[i][j]);
    }
};

不同路径 III

**思路：**直接把这道题当做一个迷宫问题，从起点开始深搜，找能走到终点的路径，然后记录这条路径中遇到的 0 的个数，如果这条路径中 0 的个数和二维矩阵中 0 的个数相等，那么这条路径就是符合题目要求的。

代码：

cpp 复制代码 
class Solution {
    bool vis[21][21];
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int ret = 0;
    int step = 0;
    int m;
    int n;
public:
    int uniquePathsIII(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int bx = 0, by = 0;

        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] == 0)
                {
                    step++;
                }
                else if(grid[i][j] == 1)
                {
                    bx = i;
                    by = j;
                    vis[i][j] = true;
                }
            }
        }

        dfs(grid, bx, by, 0);
        return ret;
    }

    void dfs(vector<vector<int>>& grid, int i, int j, int count)
    {
        if(grid[i][j] == 0)
            count++;

        if(grid[i][j] == 2)
        {
            if(count == step)
                ret++;
        }

        for(int k = 0; k < 4; k++)
        {
            int x = i + dx[k];
            int y = j + dy[k];
            if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1)
            {
                vis[x][y] = true;
                dfs(grid, x, y, count);
                vis[x][y] = false;
            }
        }
    }
};
相关推荐
黄昏晓x1 小时前
C++----异常
android·java·c++
Highcharts.js2 小时前
如何根据派生数据创建钟形曲线图表？highcharts正态分布曲线使用指南：从创建到设置一文搞定
开发语言·javascript·开发文档·正态分布·highcharts·图表类型·钟形图
宇木灵2 小时前
C语言基础-九、动态内存分配
c语言·开发语言·学习·算法
追随者永远是胜利者2 小时前
（LeetCode-Hot100）301. 删除无效的括号
java·算法·leetcode·职场和发展·go
楼田莉子2 小时前
Linux网络学习：网络的基础概念
linux·运维·服务器·网络·c++·学习
追随者永远是胜利者2 小时前
（LeetCode-Hot100）239. 滑动窗口最大值
java·算法·leetcode·职场和发展·go
im_AMBER2 小时前
Leetcode 126 两数之和 II - 输入有序数组 | 盛最多水的容器
数据结构·学习·算法·leetcode
ShiJiuD6668889992 小时前
Java 异常 File
java·开发语言
lxl13072 小时前
C++算法（5）位运算
java·c++·算法
热门推荐
01GitHub 镜像站点02如何解决 OpenClaw “Pairing required” 报错：两种官方解决方案详解03AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot04Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services05全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）06MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法07openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南08配置 OpenClaw 使用 Ollama 本地模型09Tripo AI：构建游戏就绪的3D资产10从零搭建一个 PHP 登录注册系统（含完整源码）