hot 100 第三十五题 35.二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

复制代码

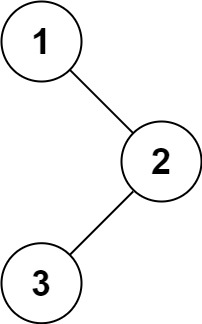
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

复制代码

输入：root = []
输出：[]

示例 3：

复制代码

输入：root = [1]
输出：[1]

核心思路

二叉树遍历有三种方式：

前序：根 → 左 → 右
中序：左 → 根 → 右
后序：左 → 右 →根

中序遍历的结果对于二叉搜索树 来说是升序序列。

解法：递归（最简单）

复制代码

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }
    
    private void inorder(TreeNode node, List<Integer> result) {
        if (node == null) return;
        
        inorder(node.left, result);   // 左
        result.add(node.val);         // 根
        inorder(node.right, result);  // 右
    }
}
```

### 详细演示
```
二叉树:
    1
   / \
  2   3
 / \
4   5

递归调用栈:
inorder(1)
  ├─ inorder(2)
  │   ├─ inorder(4)
  │   │   ├─ inorder(null) 返回
  │   │   ├─ add(4) → [4]
  │   │   └─ inorder(null) 返回
  │   │
  │   ├─ add(2) → [4,2]
  │   │
  │   └─ inorder(5)
  │       ├─ inorder(null) 返回
  │       ├─ add(5) → [4,2,5]
  │       └─ inorder(null) 返回
  │
  ├─ add(1) → [4,2,5,1]
  │
  └─ inorder(3)
      ├─ inorder(null) 返回
      ├─ add(3) → [4,2,5,1,3]
      └─ inorder(null) 返回

结果: [4,2,5,1,3]
```

## 解法2：迭代（使用栈）

### 思路

用栈模拟递归的过程：
1. 一路向左，将所有左子节点入栈
2. 弹出栈顶，访问节点
3. 转向右子树，重复步骤1
```
核心：先找到最左边的节点，然后回溯

本质

中序遍历的核心：

递归思想 --- 左子树中序 + 根 + 右子树中序
模拟栈 --- 迭代用栈保存回溯路径
Morris技巧 --- 利用空指针建立临时连接

应用场景：

二叉搜索树中序遍历得到升序序列
验证二叉搜索树
二叉搜索树中第K小元素