二叉树创建和遍历

|--------------------------------------------------------------------------------------------------------------------------------|
| 个人主页：敲上瘾-CSDN博客 |
| 二叉树介绍：二叉树(详解)-CSDN博客 |

一、二叉树的创建

二、二叉树的遍历

1.前序遍历

一、二叉树的创建

关于二叉树的创建和遍历我们考虑用递归来实现。

我们通过前序遍历的数组"ABD##E#H##CF##G##" 来创建数组，其中 '#' 相当于空指针。

头文件的声明：

cpp 复制代码

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

cpp 复制代码

BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (*pi == n)
		return NULL;
	int val = a[(*pi)++];
	if (val == '#')
		return NULL;
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	assert(root);
	root->_data = val;
	root->_left = BinaryTreeCreate(a, n, pi);
	root->_right = BinaryTreeCreate(a, n, pi);
	return root;
}

二、二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的结点进行相应的操作，并且每个结点只操作一次。访问结点所做的操作依赖于具体的应用问题。

遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

前序遍历(Preorder Traversal 亦称先序遍历)------访问根结点的操作发生在遍历其左右子树之前。
中序遍历(Inorder Traversal)------访问根结点的操作发生在遍历其左右子树之中（间）。
后序遍历(Postorder Traversal)------访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

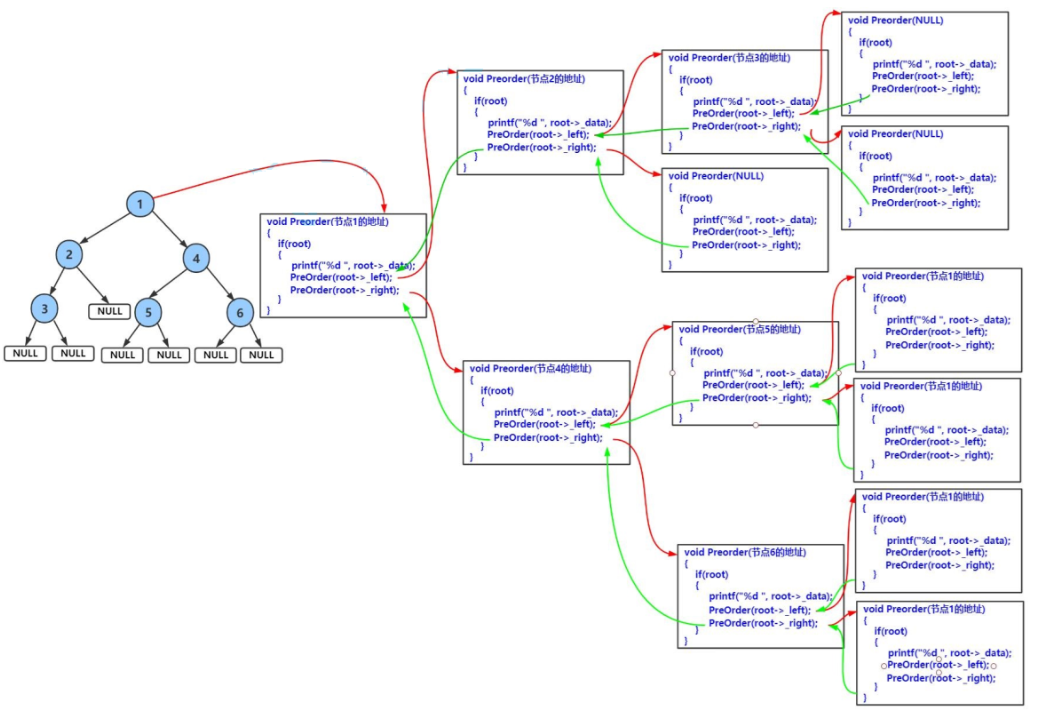
1.前序遍历

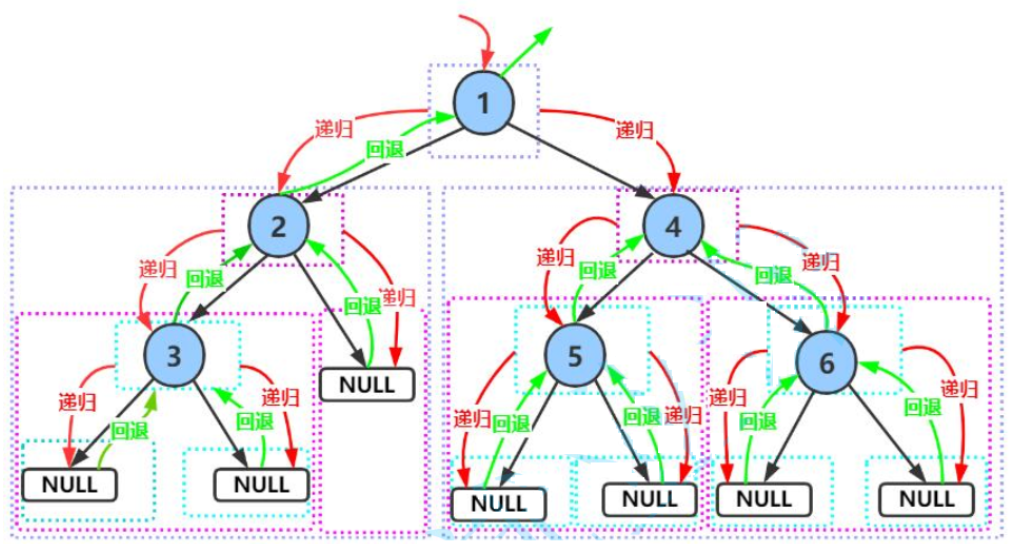
cpp 复制代码

void BinaryTreePrevOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}
	printf("%c", root->_data);
	BinaryTreePrevOrder(root->_left);
	BinaryTreePrevOrder(root->_right);
}
//或者这么写:
void PrevOrder(BTNode* root)
{
	if (root)
	{
    	printf("%c", root->_data);
    	PrevOrder(root->_left);
	    PrevOrder(root->_right);
    }
}

2.中序遍历

cpp 复制代码

void BinaryTreeInOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}
	BinaryTreeInOrder(root->_left);
	printf("%c", root->_data);
	BinaryTreeInOrder(root->_right);
}

3.后序遍历

cpp 复制代码

void BinaryTreePostOrder(BTNode* root)
{
	if (!root)
	{
		printf("#");
		return;
	}
	BinaryTreePostOrder(root->_left);
	BinaryTreePostOrder(root->_right);
	printf("%c", root->_data);
}

4.层序遍历

层序遍历是一层一层往下遍历的，并不是单个方向深入，像以上三种遍历都可以叫做深度优先遍历 ，而层序遍历也可以叫做广度优先遍历 ，它是不能用递归实现的，要实现它我们可以使用一个队列结构，我们把根节点存入队列然后对队列进行操作，把根节点拿出来(Pop)然后把它的左孩子和右孩子依次取出放入队列，然后再次从队头取到根节点重复操作，一次下去直到队列为空，就能完成层序遍历。如下：

cpp 复制代码

void BinaryTreeLevelOrder(BTNode* root)
{
	if (!root)
		return;
	Queue pt;//需要构造出一个队列结构，这里就不在展示
	QueueInit(&pt);
	QueuePush(&pt, root);
	while (!QueueEmpty(&pt))
	{
		BTNode* pf = QueueFront(&pt);
		if (pf)
			printf("%c", pf->_data);
		else
			printf("#");
		QueuePop(&pt);
		if (pf)
		{
			QueuePush(&pt, pf->_left);
			QueuePush(&pt, pf->_right);
		}
	}
}

三、相关计算

1.总节点个数计算

在计算节点个数的时候，初学着可能会想用一个全局变量，用以上任意方法遍历并计数。这种方法是可行的但不太可靠。像这些二叉树相关的计算我们大多数都可以考虑把它化为小问题去分析。如果是空树的话就是0，如果不是空树就是1+左树的节点个数+右树的节点个数，像这样左树又可以分为左树和右树去解决，可以不断的把问题化小。如下：

cpp 复制代码

int BinaryTreeSize(BTNode* root)
{
	if (!root)
		return 0;
	else
		return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

2.叶子节点个数计算

这个计算和上一个方法是相似的，不过我们得特别判断以下是否为叶子节点。如下：

cpp 复制代码

int BinaryTreeLeafSize(BTNode* root)
{
	if (!root)
		return 0;
	if (!root->_left && !root->_right)
		return 1;
	return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

3.深度计算

求一颗树的深度可以化为就是左子树的深度和右子树中的最大深度，而左子树又可以在化为更小的左右子树的深度就如此递推下去，直到遇到空树才一次回归(返回)，这样就把大问题化为小问题用递归实现。如下：

cpp 复制代码

int BinaryTreeHeight(BTNode* root)
{
	if (!root)
		return 0;
	int v1=BinaryTreeHeight(root->_left);
	int v2 = BinaryTreeHeight(root->_right);
	return v1 > v2 ? v1 + 1 : v2 + 1;
}

要注意一点的是千万不要写成下面的方式：

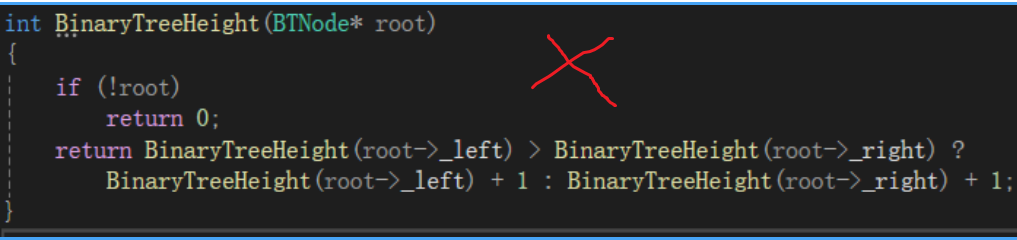
这样会使一个函数内就有三个递归展开，效率会变得非常非常低。