在数据科学竞赛中,梯度提升模型(Gradient Boosting)是一种非常强大的工具,它能够将多个弱学习模型组合起来,形成一个强学习模型。这个过程是通过逐步添加弱学习者来实现的,每个新加入的弱学习者都专注于当前整体模型的弱点,从而逐步提高预测的准确性。
什么梯度提升
这里先介绍梯度提升原理,而无需深入其背后的复杂数学。一旦掌握了梯度提升在宏观层面的运作原理,再进一步探索那些支撑其强大功能的数学基础。
首先,让我们来定义一下"提升"学习者的含义。通过巧妙地调整学习模型的特性,即便是表现平庸的弱学习器也能蜕变为一个强大的预测者。那么,究竟是哪些学习算法在接受这种提升呢?
Boosting模型的魔法在于它能够增强另一种常见的机器学习模型------决策树。
决策树通过将数据集细分为越来越小的片段来构建模型,直至每个子集无法进一步划分,最终形成一棵由节点和叶子组成的树。在决策树中,节点代表了基于不同过滤标准对数据点进行决策的点,而叶子则是已经分类的数据点。决策树算法能够处理数值型数据和分类数据,树中的每个分割都是基于特定的变量或特征进行的。
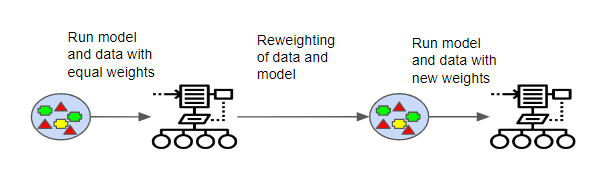
一种著名的Boosting算法是AdaBoost算法。AdaBoost算法首先训练一个决策树模型,并为每个观察值分配相同的权重。在评估了第一棵树的准确性之后,它会调整不同观察值的权重,降低那些易于分类的观察值的权重,同时增加那些难以分类的观察值的权重。然后,使用这些调整后的权重创建第二棵树,目的是使第二棵树的预测比第一棵树更加精确。
此时,模型由原始树和新树(即树1 + 树2)的预测组成。再次基于新模型评估分类精度,然后根据模型计算出的误差创建第三棵树,并再次调整权重。这个过程会持续进行,直到达到预定的迭代次数。最终,我们得到的是一个集成模型,它综合了所有之前构建的树的预测,形成一个加权和。
虽然上述过程使用了决策树和基础预测器/模型,但实际上可以使用多种模型(例如许多标准分类器和回归器模型)来执行这种增强方法。关键的理解点在于,后续的预测器会从前一个预测器所犯的错误中学习,并且这些预测器是按照顺序创建的。
增强算法的一个主要优势是,与其他机器学习模型相比,它们在找到当前预测时所需的时间更少。然而,使用增强算法时需要谨慎,因为它们存在过度拟合的风险。
通过这种润色,我们希望您能对梯度提升有一个更直观的理解,并激发您进一步探索这一领域的兴趣。
梯度提升
我们现在来看看最常见的增强算法之一。 梯度提升模型 (GBM) 以其高精度而闻名,它们增强了 AdaBoost 中使用的一般原理。
梯度提升模型和 AdaBoost 之间的主要区别在于 GBM 使用不同的方法来计算哪些学习者错误识别了数据点。 AdaBoost 通过检查权重较大的数据点来计算模型表现不佳的地方。 同时,GBM 使用梯度来确定学习者的准确性,将损失函数应用于模型。 损失函数是一种衡量模型在数据集上的拟合准确性、计算误差并优化模型以减少误差的方法。 GBM 允许用户根据其期望的目标优化指定的损失函数。
采用最常见的损失函数------ 均方误差 - 举个例子, 梯度下降用于根据预定义的学习率更新预测,旨在找到损失最小的值。
为了更清楚一点:
新模型预测=输出变量-旧的不完美预测。
从更统计学的角度来看,GBM 的目标是在模型残差中找到相关模式,调整模型以适应该模式并使残差尽可能接近于零。 如果您要对模型的预测进行回归,残差将分布在 0 附近(完美拟合),并且 GBM 会在残差中查找模式并围绕这些模式更新模型。
换句话说,更新预测以使所有残差之和尽可能接近 0,这意味着预测值将非常接近实际值。
请注意,GBM 可以使用多种其他损失函数(例如对数损失)。 上面选择 MSE 是为了简单起见。
梯度提升模型的变体
梯度提升模型是贪婪算法,很容易在数据集上过度拟合。 这可以通过以下方法来防范 几种不同的方法 可以提高 GBM 的性能。
GBM 可以通过四种不同的方法进行调节:收缩、树约束、随机梯度提升和惩罚学习。
收缩
如前所述,在 GBM 中,预测以顺序方式汇总在一起。 在"收缩"中,每棵树对总和的添加都会进行调整。 应用权重会减慢算法的学习速度,从而需要向模型中添加更多树,这通常会提高模型的鲁棒性和性能。 代价是模型需要更长的时间来训练。
树约束
通过各种调整来约束树,例如增加树的深度或增加树中节点或叶子的数量,可以使模型更难过度拟合。 对每次分割的最小观察数施加限制也有类似的效果。 再次强调,代价是模型的训练时间会更长。
随机抽样
可以根据训练数据集随机选择的子样本,通过随机过程创建个体学习器。 这具有减少树之间的相关性的效果,从而防止过度拟合。 可以在创建树之前或考虑树的分割之前对数据集进行二次采样。
惩罚性学习
除了通过限制树的结构来约束模型之外,还可以使用回归树。 回归树的每个叶子都附加有数值,这些数值充当权重,并且可以使用常见的正则化函数(如 L1 和 L2 正则化)进行调整。