每一步向前都是向自己的梦想更近一步,坚持不懈,勇往直前!
第一题:106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
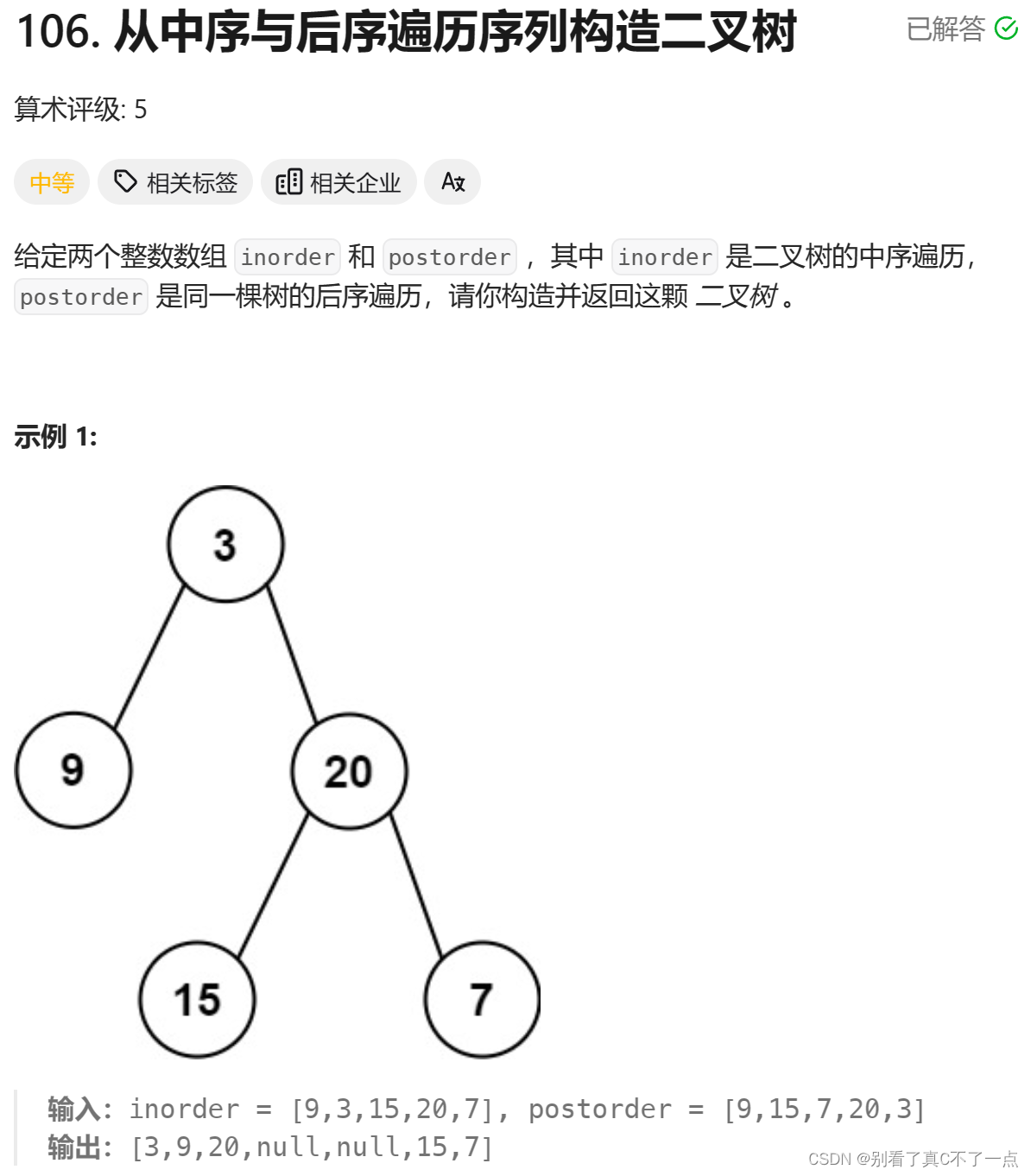
java
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
Map<Integer, Integer> map = new HashMap<>();
//把中序每个点都记录下来
for(int i = 0; i < inorder.length; i++){
map.put(inorder[i], i);
}
//传入后序的最后一个节点,因为是根节点
TreeNode head = helper(0, inorder.length - 1, map, postorder, postorder.length - 1);
return head;
}
private static TreeNode helper(int low, int high, Map<Integer, Integer> map, int[] postorder, int idx){
if(low > high){
return null;
}
//找到对应的值
int val = postorder[idx];
//在中序中找到分割点
int index = map.get(val);
TreeNode node = new TreeNode(val);
//递归找到左右子树
node.left = helper(low, index - 1, map, postorder, idx - (high - index) - 1);
node.right = helper(index + 1, high, map, postorder, idx - 1);
return node;
}
}第二题:107. 二叉树的层序遍历 II - 力扣(LeetCode)
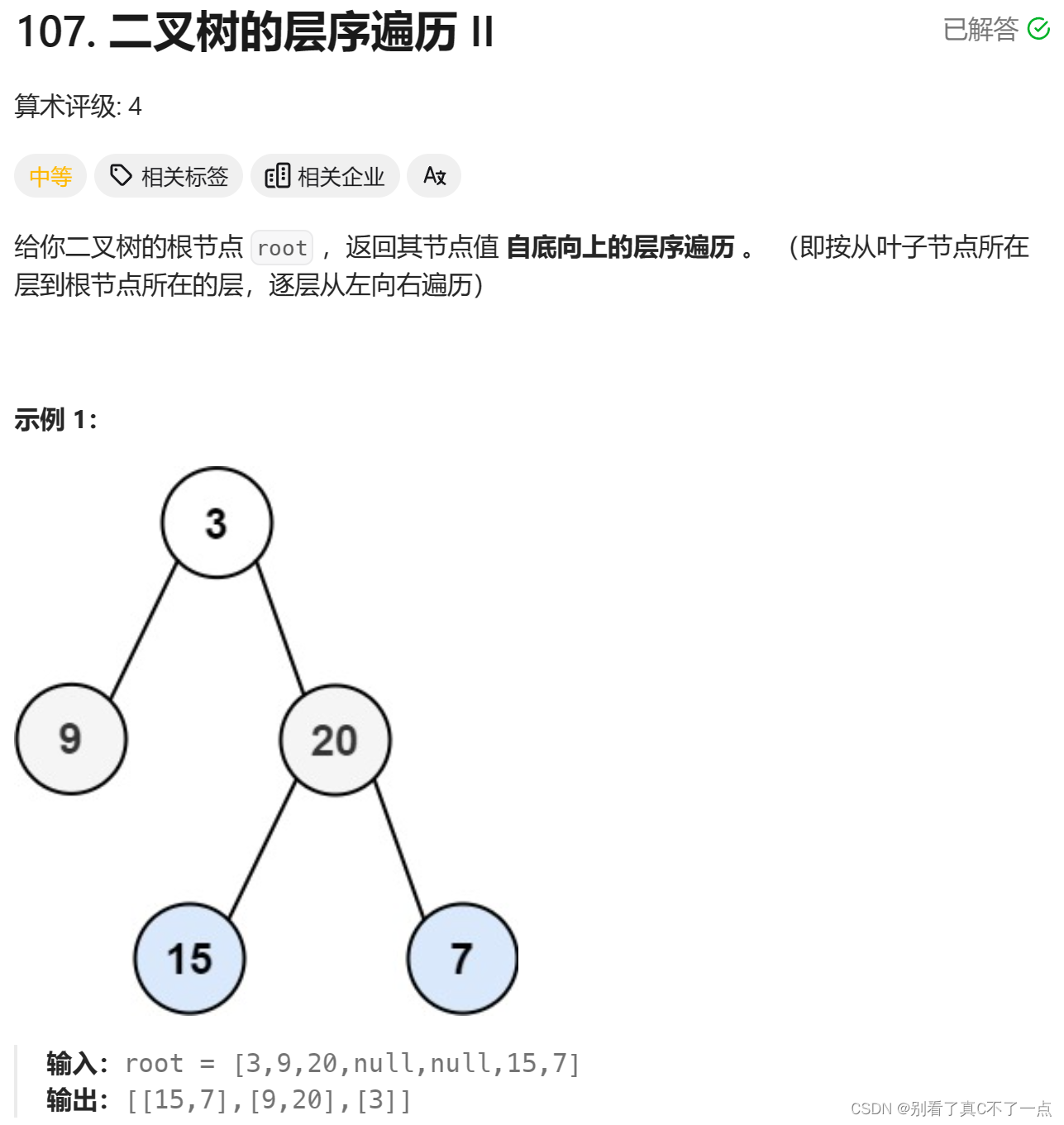
java
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
//就是使用栈每次把每一层记录下来,最后逆序输出
//本质上还是属于层序遍历
List<List<Integer>> res = new ArrayList<>();
if(root == null){
return res;
}
Deque<TreeNode> stack = new ArrayDeque<>();
stack.offer(root);
while(!stack.isEmpty()){
List<Integer> tmp = new ArrayList<>();
int size = stack.size();
for(int i = 0; i < size; i++){
TreeNode cur_node = stack.poll();
tmp.add(cur_node.val);
if(cur_node.left != null){
stack.offer(cur_node.left);
}
if(cur_node.right != null){
stack.offer(cur_node.right);
}
}
res.add(0,tmp);
}
return res;
}
}第三题:108. 将有序数组转换为二叉搜索树 - 力扣(LeetCode)
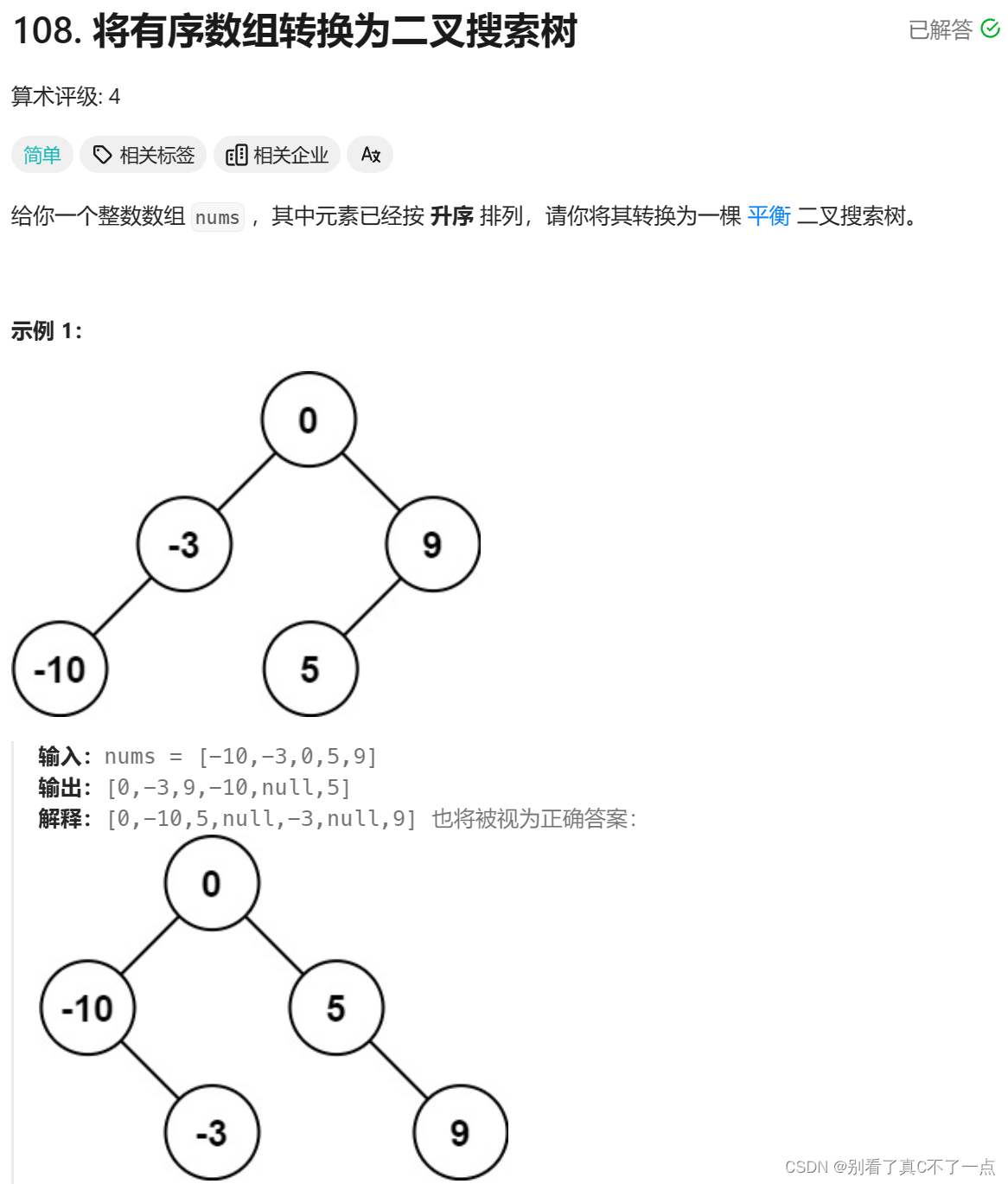
java
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
//题目提到有序,二叉,高度要平衡,
//相当于每次我们找到节点都是要中间节点
//随后向两边扩散,所以创建二叉搜索树的时候一定要二叉
return helper(nums, 0 , nums.length - 1);
}
private TreeNode helper(int[] nums, int left, int right){
if(left > right){
return null;
}
//找到中间节点
int mid = left + (right - left) / 2;
TreeNode node = new TreeNode(nums[mid]);
//递归
node.left = helper(nums, left, mid - 1);
node.right = helper(nums, mid + 1, right);
//注意是返回某个节点
return node;
}
}第四题:109. 有序链表转换二叉搜索树 - 力扣(LeetCode)
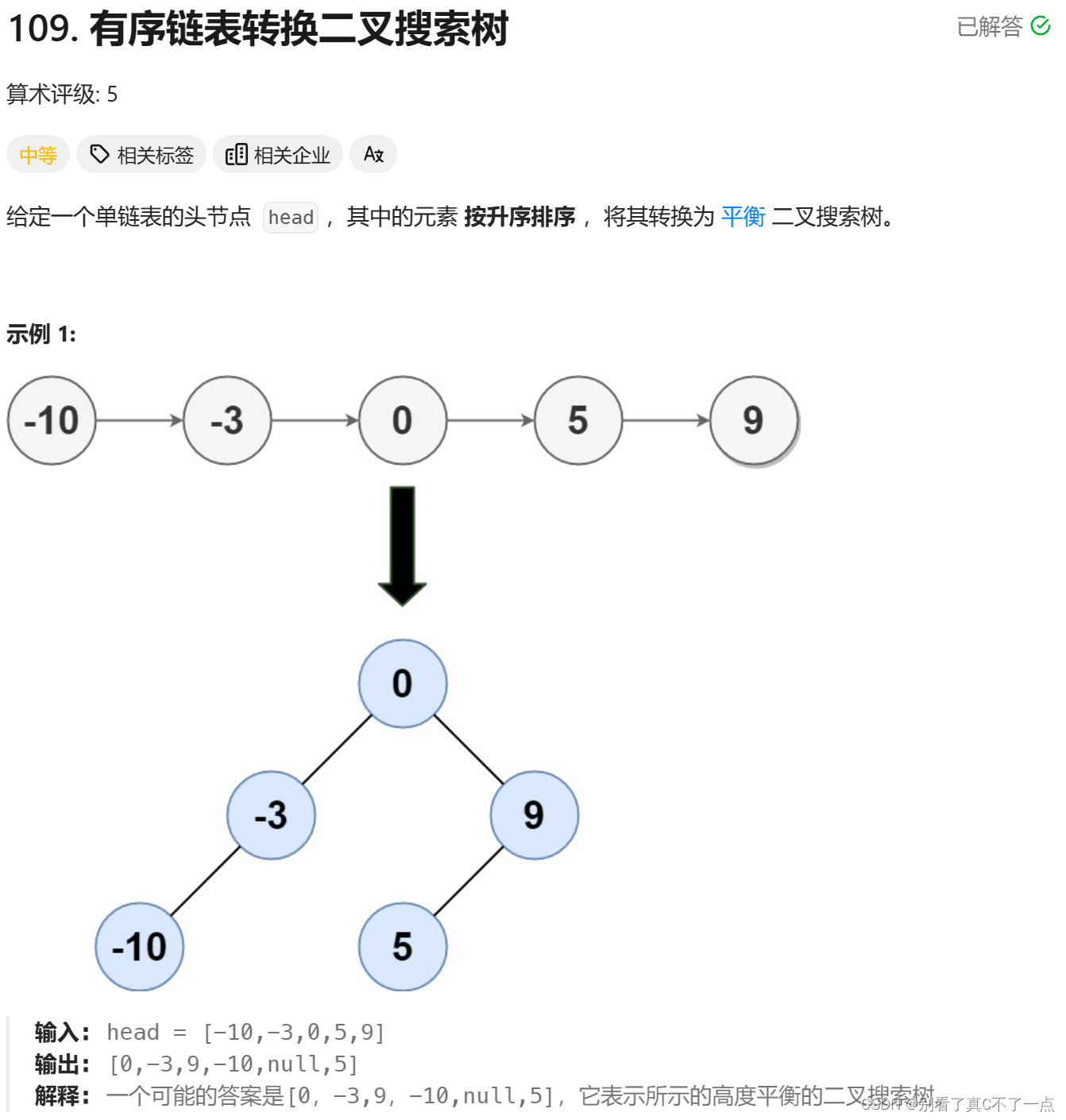
java
class Solution {
public TreeNode sortedListToBST(ListNode head) {
if (head == null) {
return null; // 基本情况
}
return convertToBST(head, null);
}
private TreeNode convertToBST(ListNode head, ListNode tail) {
if (head == tail) {
return null; // 基本情况:子列表为空
}
//使用快慢指针来实现二分中查找中位的过程
ListNode slow = head;
ListNode fast = head;
while (fast != tail && fast.next != tail) {
slow = slow.next;
fast = fast.next.next;
}
TreeNode root = new TreeNode(slow.val);
root.left = convertToBST(head, slow);
root.right = convertToBST(slow.next, tail);
return root;
}
}
java
class Solution {
public boolean isBalanced(TreeNode root) {
//对于每一个点进行递归判断
return getH(root) != -1;
}
private static int getH(TreeNode node){
//对于每一个特定的点,如果为空则高度为0
if(node == null){
return 0;
}
//找到左边,如果左边不满足,则自身也不满足
int left = getH(node.left);
if(left == -1){
return -1;
}
//同理,右边同样逻辑
int right = getH(node.right);
if(right == -1){
return -1;
}
//注意下面判别式,判断左右高度差值是否大于1
//大了肯定不满足了
//否则我们给出一个最大高度
if(Math.abs(left - right) > 1){
return -1;
}else{
return Math.max(left, right) + 1;
}
}
}