指数分布
指数分布(Exponential Distribution)是一种常见的连续型概率分布,通常用于描述事件之间的时间间隔。假设随机变量 ( X ) 服从参数为 ( \lambda ) 的指数分布,记作 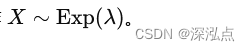
指数分布的概率密度函数(PDF)为:
f ( x ) = { λ e − λ x x ≥ 0 0 x < 0 f(x) = \begin{cases} \lambda e^{-\lambda x} & x \geq 0 \\ 0 & x < 0 \end{cases} f(x)={λe−λx0x≥0x<0
期望值
期望值(Expectation)表示随机变量的平均值。对于指数分布 ( X ),其期望值 ( \mathbb{E}(X) ) 定义为:
E ( X ) = ∫ 0 ∞ x f ( x ) d x \mathbb{E}(X) = \int_{0}^{\infty} x f(x) \, dx E(X)=∫0∞xf(x)dx
代入指数分布的概率密度函数:
E ( X ) = ∫ 0 ∞ x λ e − λ x d x \mathbb{E}(X) = \int_{0}^{\infty} x \lambda e^{-\lambda x} \, dx E(X)=∫0∞xλe−λxdx
将 (\lambda) 提取出来:
E ( X ) = λ ∫ 0 ∞ x e − λ x d x \mathbb{E}(X) = \lambda \int_{0}^{\infty} x e^{-\lambda x} \, dx E(X)=λ∫0∞xe−λxdx
为了计算这个积分,我们使用分部积分法。设:
u = x , d v = e − λ x d x u = x, \quad dv = e^{-\lambda x} \, dx u=x,dv=e−λxdx
则:
d u = d x , v = − 1 λ e − λ x du = dx, \quad v = -\frac{1}{\lambda} e^{-\lambda x} du=dx,v=−λ1e−λx
应用分部积分公式 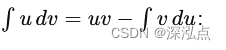
∫ 0 ∞ x e − λ x d x = − x λ e − λ x ∣ 0 ∞ + ∫ 0 ∞ 1 λ e − λ x d x \int_{0}^{\infty} x e^{-\lambda x} \, dx = \left. -\frac{x}{\lambda} e^{-\lambda x} \right|{0}^{\infty} + \int{0}^{\infty} \frac{1}{\lambda} e^{-\lambda x} \, dx ∫0∞xe−λxdx=−λxe−λx 0∞+∫0∞λ1e−λxdx
第一个项在 ( x = 0 ) 时为 0,在 ( x \to \infty ) 时也趋近于 0,因此:
− x λ e − λ x ∣ 0 ∞ = 0 \left. -\frac{x}{\lambda} e^{-\lambda x} \right|_{0}^{\infty} = 0 −λxe−λx 0∞=0
第二个项为:
∫ 0 ∞ 1 λ e − λ x d x = 1 λ ∫ 0 ∞ e − λ x d x = 1 λ [ − 1 λ e − λ x ] 0 ∞ = 1 λ ( 0 − ( − 1 ) ) = 1 λ 2 \int_{0}^{\infty} \frac{1}{\lambda} e^{-\lambda x} \, dx = \frac{1}{\lambda} \int_{0}^{\infty} e^{-\lambda x} \, dx = \frac{1}{\lambda} \left[ -\frac{1}{\lambda} e^{-\lambda x} \right]_{0}^{\infty} = \frac{1}{\lambda} \left( 0 - (-1) \right) = \frac{1}{\lambda^2} ∫0∞λ1e−λxdx=λ1∫0∞e−λxdx=λ1[−λ1e−λx]0∞=λ1(0−(−1))=λ21
因此,
E ( X ) = λ ⋅ 1 λ 2 = 1 λ \mathbb{E}(X) = \lambda \cdot \frac{1}{\lambda^2} = \frac{1}{\lambda} E(X)=λ⋅λ21=λ1
方差
方差(Variance)表示随机变量与其期望值之间的离散程度。方差的定义为:
Var ( X ) = E [ ( X − E ( X ) ) 2 ] = E ( X 2 ) − ( E ( X ) ) 2 \text{Var}(X) = \mathbb{E}[(X - \mathbb{E}(X))^2] = \mathbb{E}(X^2) - (\mathbb{E}(X))^2 Var(X)=E[(X−E(X))2]=E(X2)−(E(X))2
首先,我们计算 ( \mathbb{E}(X^2) ):
E ( X 2 ) = ∫ 0 ∞ x 2 f ( x ) d x \mathbb{E}(X^2) = \int_{0}^{\infty} x^2 f(x) \, dx E(X2)=∫0∞x2f(x)dx
代入指数分布的概率密度函数:
E ( X 2 ) = ∫ 0 ∞ x 2 λ e − λ x d x \mathbb{E}(X^2) = \int_{0}^{\infty} x^2 \lambda e^{-\lambda x} \, dx E(X2)=∫0∞x2λe−λxdx
将 (\lambda) 提取出来:
E ( X 2 ) = λ ∫ 0 ∞ x 2 e − λ x d x \mathbb{E}(X^2) = \lambda \int_{0}^{\infty} x^2 e^{-\lambda x} \, dx E(X2)=λ∫0∞x2e−λxdx
为了计算这个积分,我们再次使用分部积分法。设:
u = x 2 , d v = e − λ x d x u = x^2, \quad dv = e^{-\lambda x} \, dx u=x2,dv=e−λxdx
则:
d u = 2 x d x , v = − 1 λ e − λ x du = 2x \, dx, \quad v = -\frac{1}{\lambda} e^{-\lambda x} du=2xdx,v=−λ1e−λx
应用分部积分公式 
∫ 0 ∞ x 2 e − λ x d x = − x 2 λ e − λ x ∣ 0 ∞ + ∫ 0 ∞ 2 x λ e − λ x d x \int_{0}^{\infty} x^2 e^{-\lambda x} \, dx = \left. -\frac{x^2}{\lambda} e^{-\lambda x} \right|{0}^{\infty} + \int{0}^{\infty} \frac{2x}{\lambda} e^{-\lambda x} \, dx ∫0∞x2e−λxdx=−λx2e−λx 0∞+∫0∞λ2xe−λxdx
第一个项在 ( x = 0 ) 时为 0,在 ( x \to \infty ) 时也趋近于 0,因此:
− x 2 λ e − λ x ∣ 0 ∞ = 0 \left. -\frac{x^2}{\lambda} e^{-\lambda x} \right|_{0}^{\infty} = 0 −λx2e−λx 0∞=0
第二个项为:
∫ 0 ∞ 2 x λ e − λ x d x = 2 λ ∫ 0 ∞ x e − λ x d x \int_{0}^{\infty} \frac{2x}{\lambda} e^{-\lambda x} \, dx = \frac{2}{\lambda} \int_{0}^{\infty} x e^{-\lambda x} \, dx ∫0∞λ2xe−λxdx=λ2∫0∞xe−λxdx
我们之前已经计算过这个积分:
∫ 0 ∞ x e − λ x d x = 1 λ 2 \int_{0}^{\infty} x e^{-\lambda x} \, dx = \frac{1}{\lambda^2} ∫0∞xe−λxdx=λ21
因此,
E ( X 2 ) = λ ⋅ 2 λ ⋅ 1 λ 2 = 2 λ 2 \mathbb{E}(X^2) = \lambda \cdot \frac{2}{\lambda} \cdot \frac{1}{\lambda^2} = \frac{2}{\lambda^2} E(X2)=λ⋅λ2⋅λ21=λ22
现在我们可以计算方差:
Var ( X ) = E ( X 2 ) − ( E ( X ) ) 2 = 2 λ 2 − ( 1 λ ) 2 = 2 λ 2 − 1 λ 2 = 1 λ 2 \text{Var}(X) = \mathbb{E}(X^2) - (\mathbb{E}(X))^2 = \frac{2}{\lambda^2} - \left(\frac{1}{\lambda}\right)^2 = \frac{2}{\lambda^2} - \frac{1}{\lambda^2} = \frac{1}{\lambda^2} Var(X)=E(X2)−(E(X))2=λ22−(λ1)2=λ22−λ21=λ21
结论
对于指数分布 
,其期望值和方差分别为:
E ( X ) = 1 λ \mathbb{E}(X) = \frac{1}{\lambda} E(X)=λ1
Var ( X ) = 1 λ 2 \text{Var}(X) = \frac{1}{\lambda^2} Var(X)=λ21
这些结果表明,在进行一系列独立的指数分布事件中,事件之间时间间隔的平均值是 ( \frac{1}{\lambda} ),而离散程度由 ( \frac{1}{\lambda^2} ) 决定。