论文阅读笔记:Instance-Aware Dynamic Neural Network Quantization
- [1 背景](#1 背景)
- [2 创新点](#2 创新点)
- [3 方法](#3 方法)
- [4 模块](#4 模块)
-
- [4.1 网络量化](#4.1 网络量化)
- [4.2 动态量化](#4.2 动态量化)
- [4.3 用于动态量化的位控制器](#4.3 用于动态量化的位控制器)
- [4.4 优化](#4.4 优化)
- [5 效果](#5 效果)
代码:https://github.com/huawei-noah/Efficient-Computing
1 背景
量化是降低深度神经网络内存和计算成本的有效方法,其中全精度的权重和激活使用低比特值表示。在大多数现有的量化方法中,每一层的位宽都是静态的,即给定数据集中的所有样本都是一样的。然而,自然图像具有巨大的多样性和丰富的内容,对所有样本使用这种通用的量化配置不是一个最优的策略。因此,作者探索一种基于实例感知的动态量化方法,以提供更好的性能。
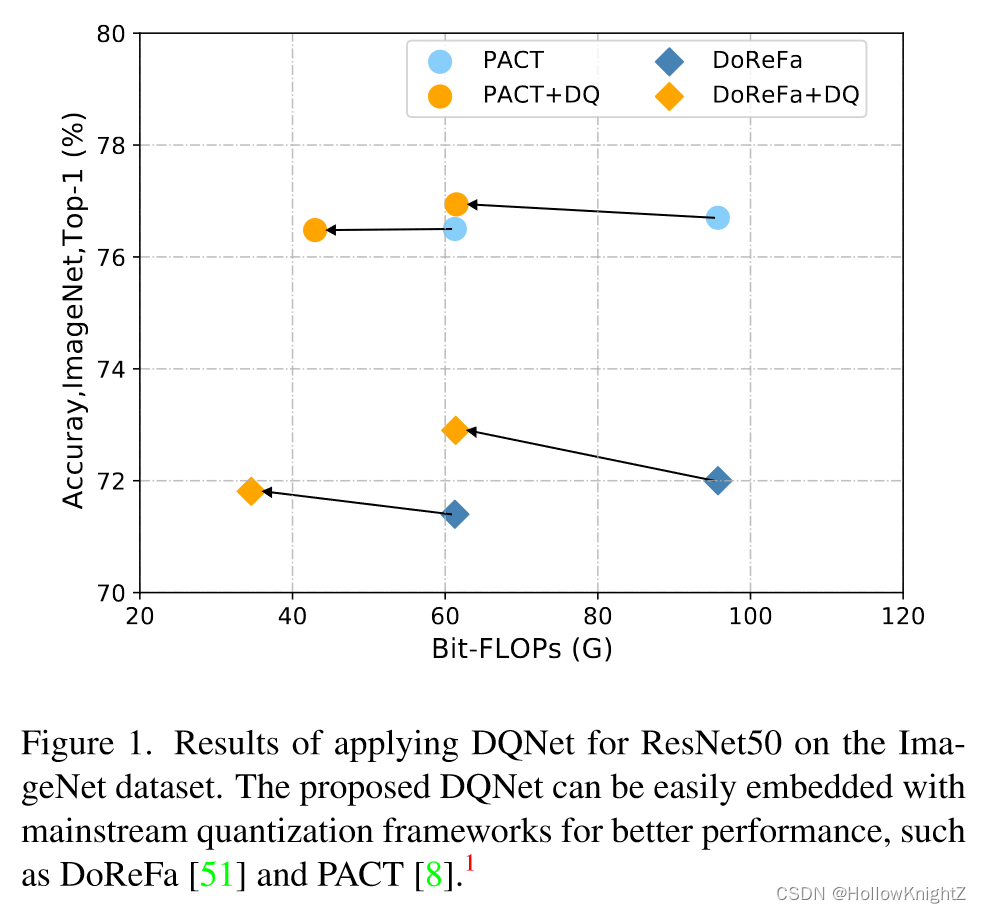
提出的方法可以很容易嵌入到主流的量化框架并获得更好的表现,如图1。
2 创新点
本文提出了一种新的网络量化方案,它在每个输入样本的条件下动态分配量化神经网络的位宽。
3 方法
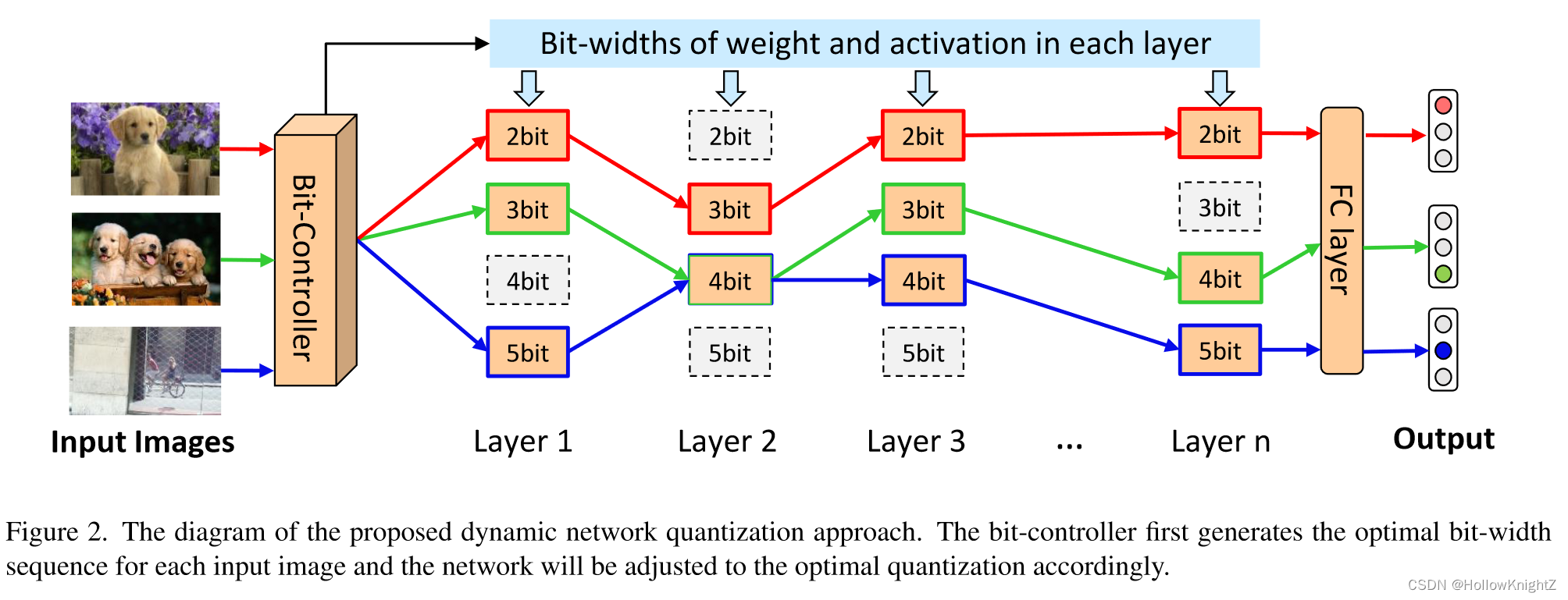
如图2,本文方法从给定的网络体系结构中派生出大量具有不同位宽配置的隐藏子网络,在推理过程中,一个难以准确识别的图像将被分配到一个更大的网络中,反之亦然。对于任意一幅图,位控制器用于预测其中所有层的权重和激活的最佳位宽序列。位控制器采用轻量级架构进行设计,使其额外的计算成本可以忽略。量化后的神经网络以端到端的方式与比特控制器一起训练,以获得更好的性能。由于动态量化网络( DQNet )可以根据不同的输入图像提供最佳的位宽配置,因此可以大大减少处理每个样本的计算成本。
4 模块
4.1 网络量化
传统的神经网络的训练和推理基本上采用浮点数,即权值和激活都以32位精度存储。模型量化方法用低比特值表示神经网络中的权值或激活以减少计算和内存开销。为了量化权重 W i W_i Wi 和激活 A i A_i Ai,这些浮点数需要限制在一个有限的值的集合内,量化函数通常定义为:
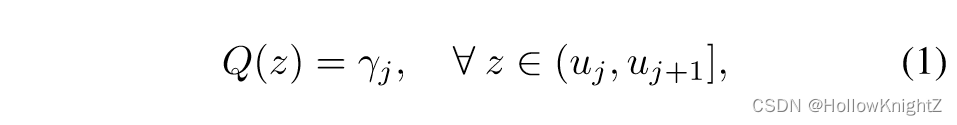
其中, ( u j , u j + 1 ] (u_j,u_{j+1}] (uj,uj+1] 表示一个是实数区间( j = 1 , ... 2 b j=1,...2^b j=1,...2b),b为量化位宽,z是输入值,即权重或激活。式(1)中的量化函数将 ( u j , u j + 1 ] (u_j,u_{j+1}] (uj,uj+1] 区间的所有的值映射到 γ j \gamma_j γj。对于对于这些区间的选择,广泛使用的策略是使用一个统一的量化函数,其中上述区间是等分的,即:
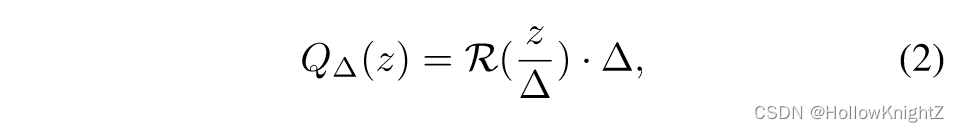
其中原值域 ( l , r ) (l,r) (l,r)被划分为 2 b 2^b 2b 个统一区间, 区间长度为 Δ = r − l 2 b \Delta=\frac{r-l}{2^b} Δ=2br−l ,R为取整函数。为了使非差分量化过程能够端到端的优化,通常采用直通估计器STE来近似量化函数的导数。
STE将量化函数的导数默认为1,即反向传播跳过此量化函数。
以dorefa_w为例(这里使用tanh函数,并用最值归一化因为实值网络中的权重值通常很小,而量化权重通常在[-1,1],这种幅度失配导致量化权重坍塌到接近零的几个量化级别):
def dorefa_w(w, nbit_w): if nbit_w == 1: w = scale_sign(w) else: w = torch.tanh(w) w = w / (2 * torch.max(torch.abs(w))) + 0.5 w = 2 * quantize(w, nbit_w) - 1 return wnbit_w=1时:
class ScaleSigner(Function): ''' take a real value x output sign(x) * E(|x|) ''' @staticmethod def forward(ctx, input): return torch.sign(input) * torch.mean(torch.abs(input)) @staticmethod def backward(ctx, grad_output): return grad_outputnbit_w>1时:
class Quantizer(Function): ''' take a real value x in alpha*[0,1] or alpha*[-1,1] output a discrete-valued x in alpha*{0, 1/(2^k-1), ..., (2^k-1)/(2^k-1)} or likeness where k is nbit ''' @staticmethod def forward(ctx, input, nbit, alpha=None, offset=None): ctx.alpha = alpha ctx.offset = offset scale = (2 ** nbit - 1) if alpha is None else (2 ** nbit - 1) / alpha ctx.scale = scale return torch.round(input * scale) / scale if offset is None \ else (torch.round(input * scale) + torch.round(offset)) / scale @staticmethod def backward(ctx, grad_output): if ctx.offset is None: return grad_output, None, None, None else: return grad_output, None, None, torch.sum(grad_output) / ctx.scale
4.2 动态量化
传统的量化方法中的比特宽度对于所有的输入通常是固定的。然而,数据集中自然图像的多样性非常高,并且大多数现有的量化算法没有考虑他们的多样性和内在复杂性。为了精确的分配计算资源,作者提出了动态量化,根据输入调整每层的位宽。假设有 K K K 个位宽候选集,即 b 1 , b 2 , ... b k b^1,b^2,...b^k b1,b2,...bk。动态量化的目的是选择一个最佳的位宽,用于量化各层的权重和激活,可以通过聚合多重位宽来制定:
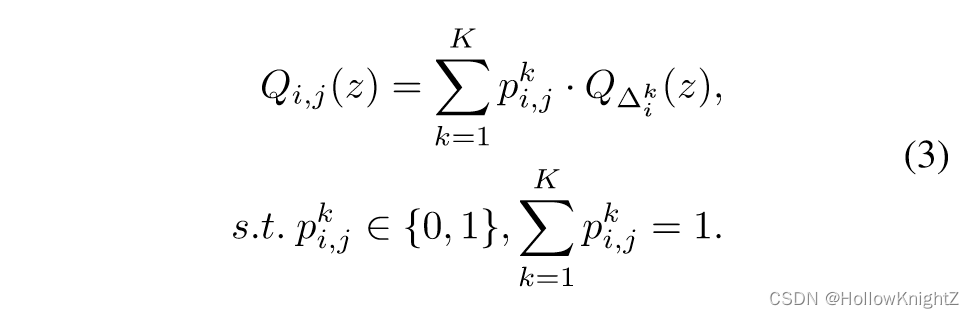
其中 p i , j k p_{i,j}^k pi,jk 表示第 i i i 层中第 j j j 个样本的第 k k k 位位宽的选择,那么第 i i i 层中第 j j j 个样本的动态量化可以表示为:
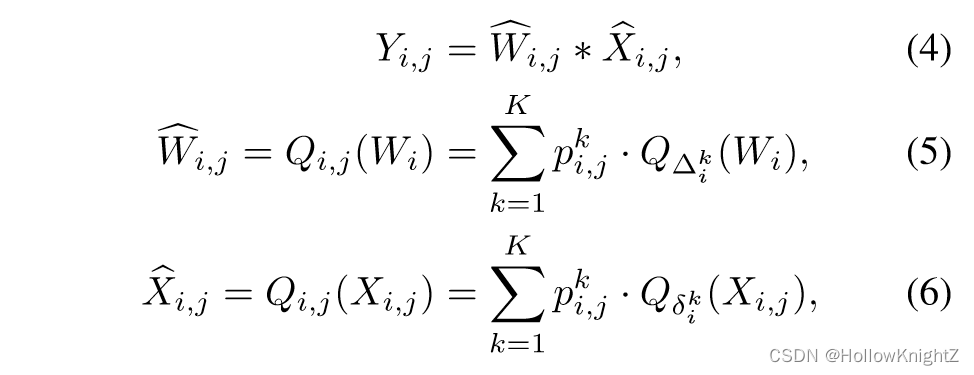
其中 Δ i k \Delta_i^k Δik 和 δ i k \delta_i^k δik 表示权重和激活的量化间隔,并且在同一层中的权重和激活应用相同的位宽, X X X 为训练输入。利用式(4)-(6,动态卷积层恰好是给定输入的混合精度层的聚合,可以通过充分挖掘所得到的量化神经网络的潜力。值得注意的是,为了方便起见,在公式中省略了偏差,偏差的量化间隔 Δ i k \Delta_i^k Δik 与时间的权重相同。
对应代码如下:
# w quan if self.nbit_w < 32: w0 = self.quan_w(self.weight, self.nbit_w-1, self.alpha_w, self.offset) w1 = self.quan_w(self.weight, self.nbit_w, self.alpha_w, self.offset) w2 = self.quan_w(self.weight, self.nbit_w+1, self.alpha_w, self.offset) else: w = self.weight # a quan if self.nbit_a < 32: x0 = self.quan_a(input, self.nbit_a-1, self.alpha_a) x1 = self.quan_a(input, self.nbit_a, self.alpha_a) x2 = self.quan_a(input, self.nbit_a+1, self.alpha_a) else: x = F.relu(input) x0 = F.conv2d(x0, w0, None, self.stride, self.padding, self.dilation, self.groups) x1 = F.conv2d(x1, w1, None, self.stride, self.padding, self.dilation, self.groups) x2 = F.conv2d(x2, w2, None, self.stride, self.padding, self.dilation, self.groups) x = x0*mask[:,0].unsqueeze(1).unsqueeze(2).unsqueeze(3)+ \ x1*mask[:,1].unsqueeze(1).unsqueeze(2).unsqueeze(3)+ \ x2*mask[:,2].unsqueeze(1).unsqueeze(2).unsqueeze(3)
式(4)-(6)不能直接优化,因为每层的选择指标 p i , j k p_{i,j}^k pi,jk 不是固定的,而是随着输入 x x x 的变化而变化。测试集无法实现获得,而对于训练数据集,选择指标的存储需求将是巨大的。例如,ResNet50,当有5个候选位宽时,每个样本可能得位宽配置数量为 5 50 = 8.8 × 1 0 34 5^{50}=8.8×10^{34} 550=8.8×1034。
4.3 用于动态量化的位控制器
为了解决上述具有挑战性的问题,作者使用一个位控制器,通过识别每个输入样本的复杂度来预测所有层的权重和激活的位宽。在实际应用中,位控制器将输出一个由预测logits组成的向量,表示每层中每个位宽候选项的选择概率。
位控制器具有极小的结构,以避免显著增加最终网络的整体内存和计算负担。具体来说,比特控制器是由主网络的前几层和一个MLP组成,实际中MLP仅由两个全连接层组成。这样,DQNet在计算量可以忽略不计的情况下预测每一层的位宽。
代码如下:
def forward(self, x): x = self.conv1(x) x = self.bn1(x) x = self.relu(x) x = self.maxpool(x) for m in self.layer1: x = m(x) feat = self.avgpool_policy(x) feat = self.fc1(feat.view(x.size(0),-1)) feat = self.dropout(feat) feat = self.fc2(feat) feat = feat.view(-1, self.num_bits) one_hot = F.gumbel_softmax(feat, tau=1, hard=True) one_hot = one_hot.view(-1, self.num_layers, self.num_bits) i = 0 for m in self.layer2: x = m(x, one_hot[:,i:i+self.block_layers,:]) i += self.block_layers for m in self.layer3: x = m(x, one_hot[:,i:i+self.block_layers,:]) i += self.block_layers for m in self.layer4: x = m(x, one_hot[:,i:i+self.block_layers,:]) i += self.block_layers x = self.avgpool(x) x = x.view(x.size(0), -1) x = self.dropout(x) x = self.fc(x) return x, one_hot
假设对于某个层的权重和激活,位控制器的输出logits为 h 1 , h 2 , ... h k h^1,h^2,...h^k h1,h2,...hk ,则位宽可以相应地选择,即 p k p^k pk 被确定为:
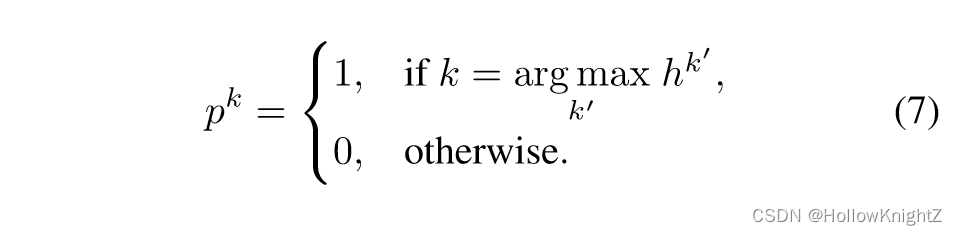
在训练和推理过程中,每层只选择1个位宽,如图3所示。
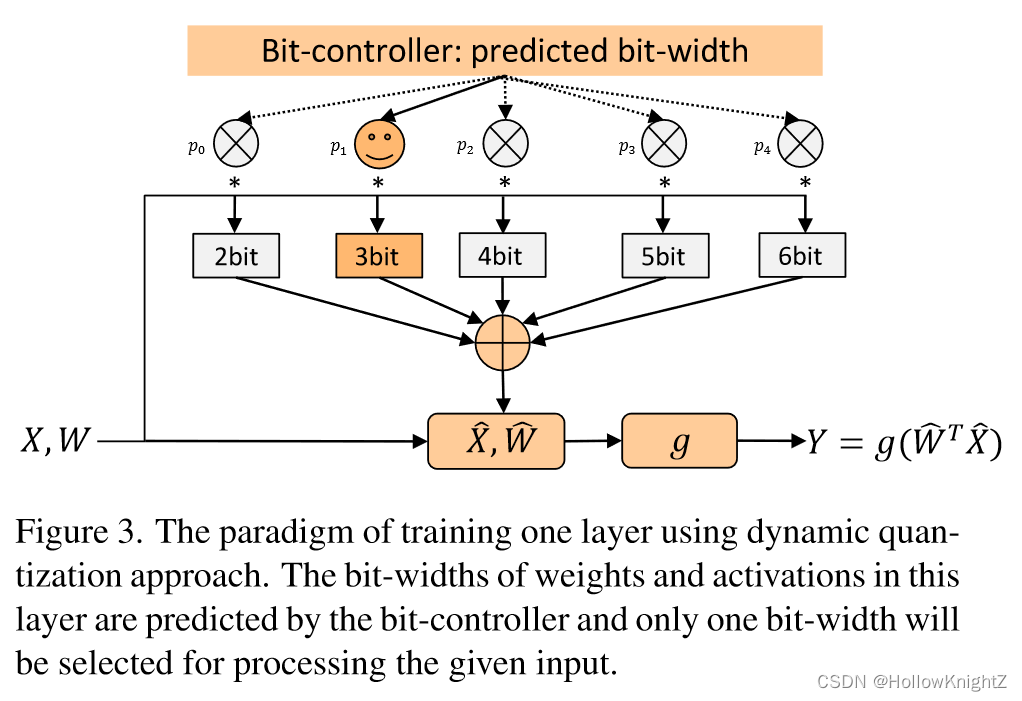
为了给argmax的采样提供一个可微的公式,在训练过程中使用Gumbel-softmax:
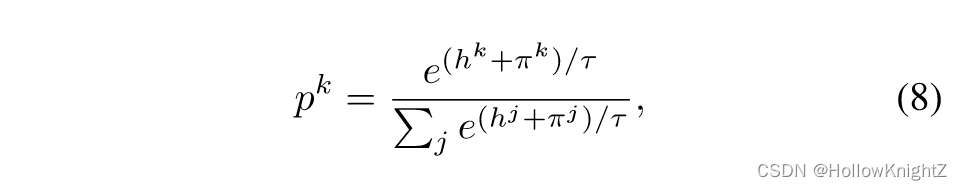
其中 τ \tau τ 是控制新样本毕竟 one-hot 向量的温度参数, π k \pi^k πk 是服从Gumbel 分布的随机噪声,如下:
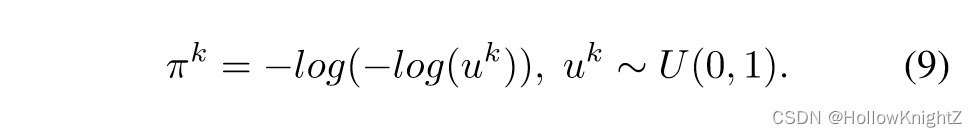
在向前过程中,针对特定的样本获取某一层的位宽后,DQNet 就会如下量化权重和激活:
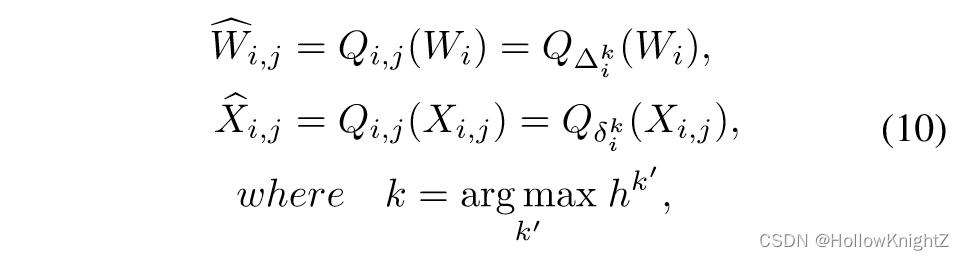
其中 Δ i k \Delta_i^k Δik 和 δ i k \delta_i^k δik 分别是预测位宽的权重和激活的量化区间。为在反向传播中,量化后的网络将利用式(8)计算出的梯度。
4.4 优化
为了灵活的控制DQNet的计算开销,作者在损失函数中加入 Bit-FLOPs压缩项。所以总损失表示为:
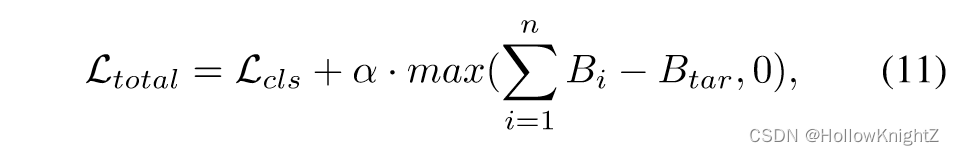
其中 B i B_i Bi 是第 i i i 层的 Bit-FLOPs, B t a r B_{tar} Btar 是量化网络的目标 Bit-FLOPs。 α \alpha α 是平衡参数。
给定一个目标Bit-FLOPs,动态量化神经网络将捕获数据集计算需求中的固有方差,并未不同实例和不同层分配最佳位宽。本文提出的动态量化方案的训练过程如算法1所示。

5 效果
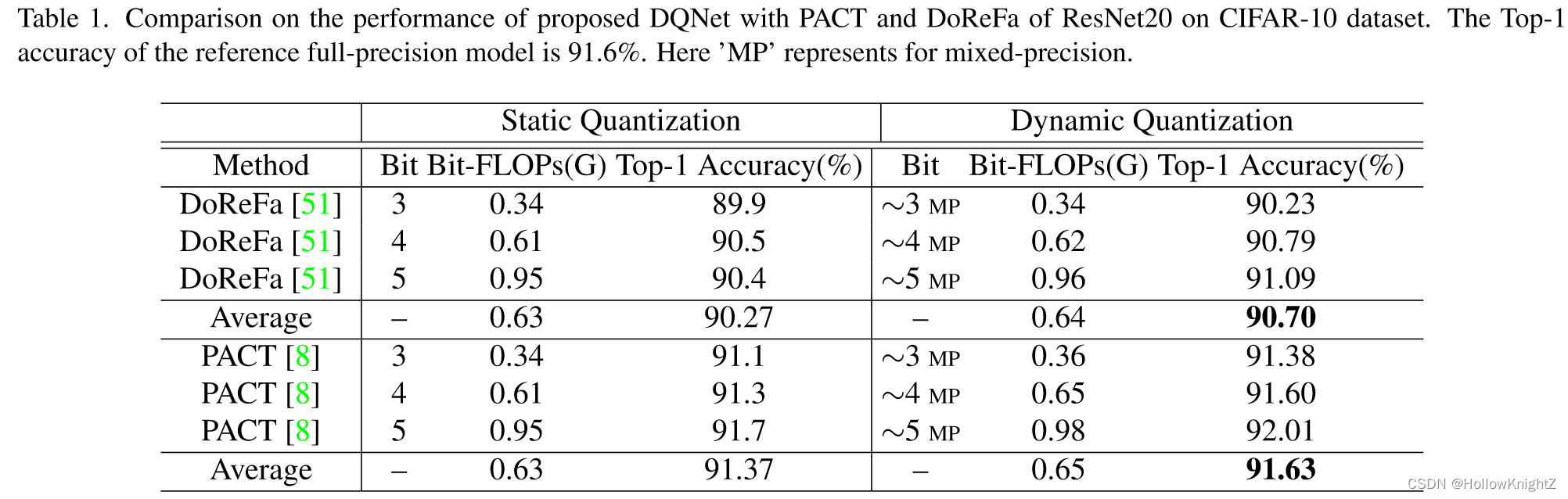
静态量化方法和使用本文提出的动态量化方法在CIFAR10数据集上的对比如表1。动态量化获得了更好的性能只需要更好的计算量。
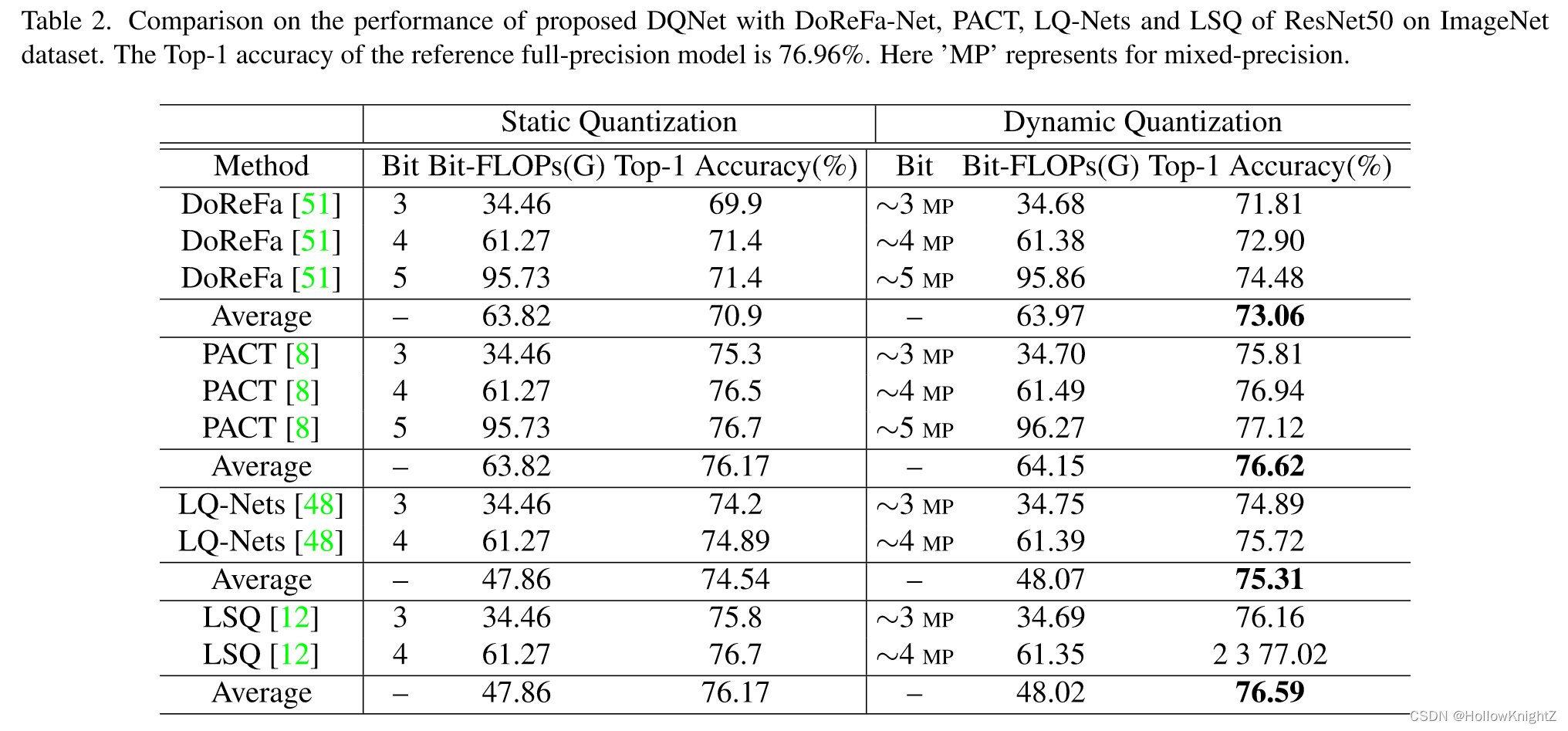
静态量化方法和使用本文提出的动态量化方法在ImageNet数据集上的对比如表2。
与混合精度方法进行比较,结果见表3。
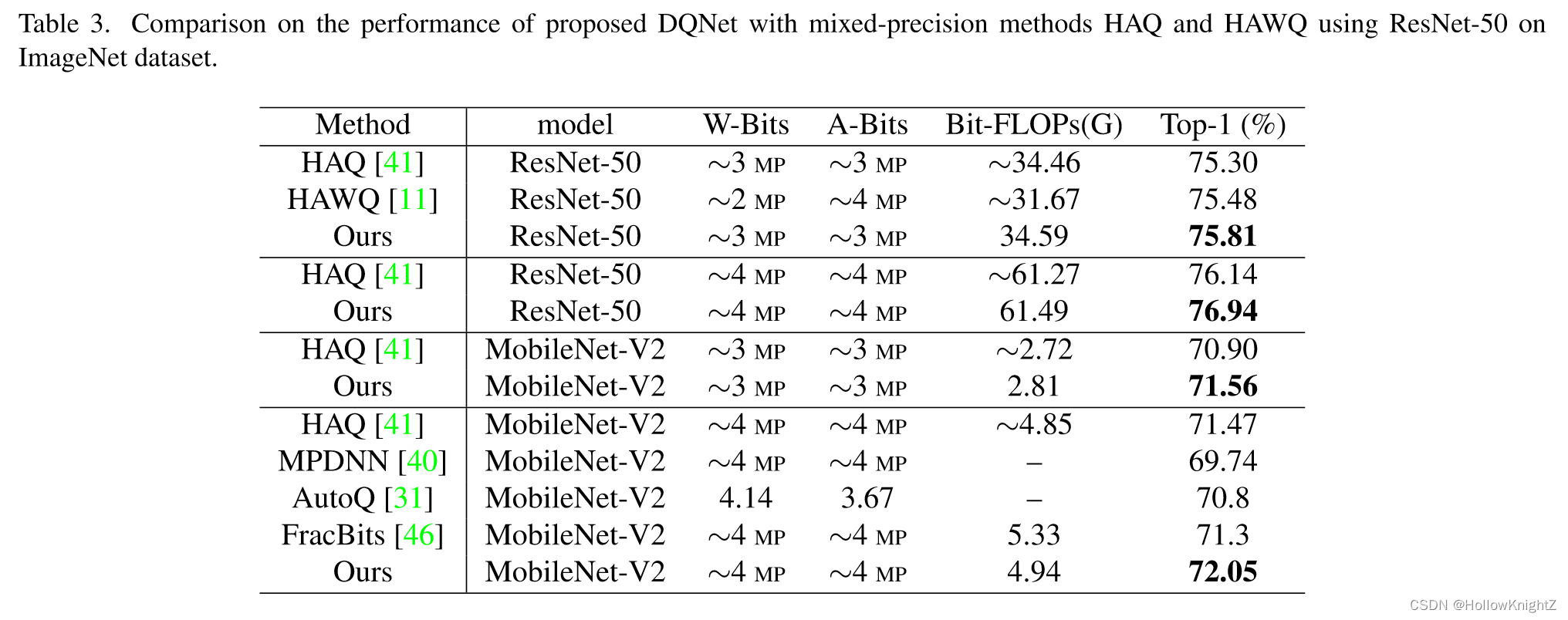
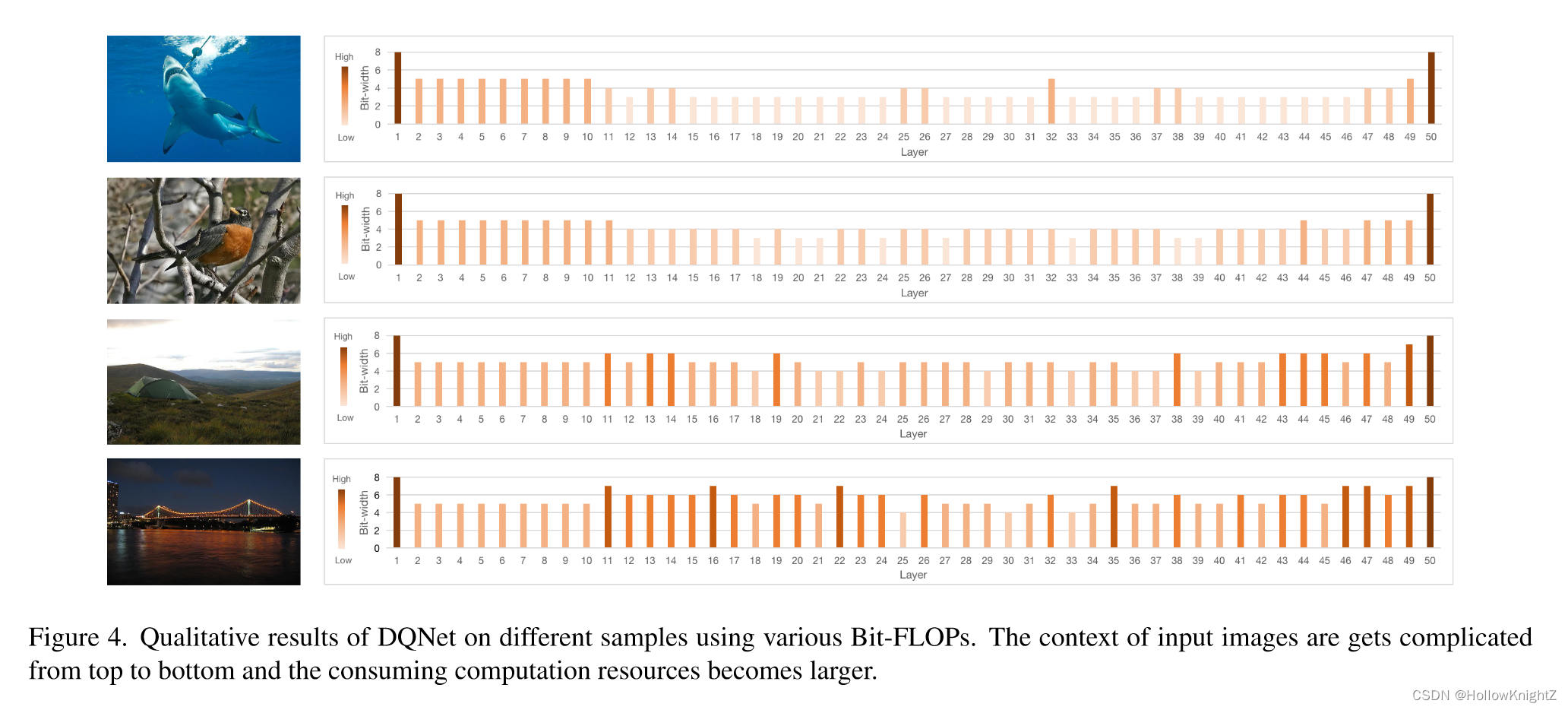
图4展示了ImageNet数据集中的部分样本,第一行使用较少的Bit-FLOPs就可以获得了正确的分类结果,而最后一行用了更多的Bit-FLOPs才可以分类正确。可以看出,使用较少的Bit-FLOPs的样本确实更容易分类,因为他们包含位于中心的单个正视物体,而需要更多计算量的样本会出现遮挡或杂乱的背景。
采用主网络的前几层作为位控制器的前端,可以明显的减少额外的计算量。作者将结果与使用单独的卷积层作为位控制器的结果进行了比较。如图5所示,与使用单独的卷积层相比,使用主网络的前几层获得了可比的结果,这引入了额外的计算开销。同时作者还测试了主网络和位控制器的共享层数对DQNet性能的影响,如图5,仅使用一个卷积层的结果甚至比静态量化结果更差,因为位控制器的表达能力不够,随着位控制器层数增加,DQNet的性能越来越好。同时,共享层不能大多,否则会对主网络产生负面影响。