1、中值滤波和萨维茨基-戈雷滤波简介
在MATLAB中,可以使用medfilt2函数来实现中值滤波。中值滤波是一种常见的滤波方法,用于去除图像中的椒盐噪声或者斑点噪声。该函数的语法为:
Matlab
filtered_image = medfilt2(input_image, [m n]);其中,input_image为待滤波的输入图像,[m n]为滤波窗口的大小,通常为奇数。中值滤波会将窗口中的像素值排序,然后取中间值作为中心像素的值,从而消除噪声。
而对于萨维茨基-戈雷滤波,可以使用wiener2函数来实现。这种滤波方法结合了均值滤波和中值滤波的优点,能够有效地去除噪声并保留图像的细节。wiener2函数的语法为:
Matlab
filtered_image = wiener2(input_image, [m n]);其中,input_image为待滤波的输入图像,[m n]为窗口的大小。萨维茨基-戈雷滤波会根据窗口内的像素值和像素值的方差来调整滤波权重,从而获得更好的滤波效果。
需要注意的是,在实际使用中,可以根据具体的图像和噪声情况来调整滤波的参数和方法,以获得最佳的滤波效果。
2、中值滤波:medfilt1()函数
说明:一维中值滤波
1)语法
语法1:y = medfilt1(x) 将输入向量x应用3阶一维中值滤波器。
语法2:y = medfilt1(x,n) 将一个n阶一维中值滤波器应用于x。
语法3:y = medfilt1(x,n,[],dim) 指定过滤器操作的维度dim。
2)参数说明
x:输入信号 y:输出信号 dim:筛选维度
3)NaN(信号数据缺失)处理
'includenan' :返回过滤信号,以便包含NaN的任何段的中值也是NaN。
'omitnan' 返回过滤后的信号,使得包含 NaN 的任何段的中值为非 NaN 值的中值。如果一个段的
所有元素都是 NaN,则结果为 NaN终点过滤,指定为'零填充'或'截断'。
'zeropad' 在端点之外,信号被视为零。 'truncate' 在接近信号边缘时计算较小段的中位数。
3、中值滤波实验
1)通过中值滤波进行降噪
代码
Matlab
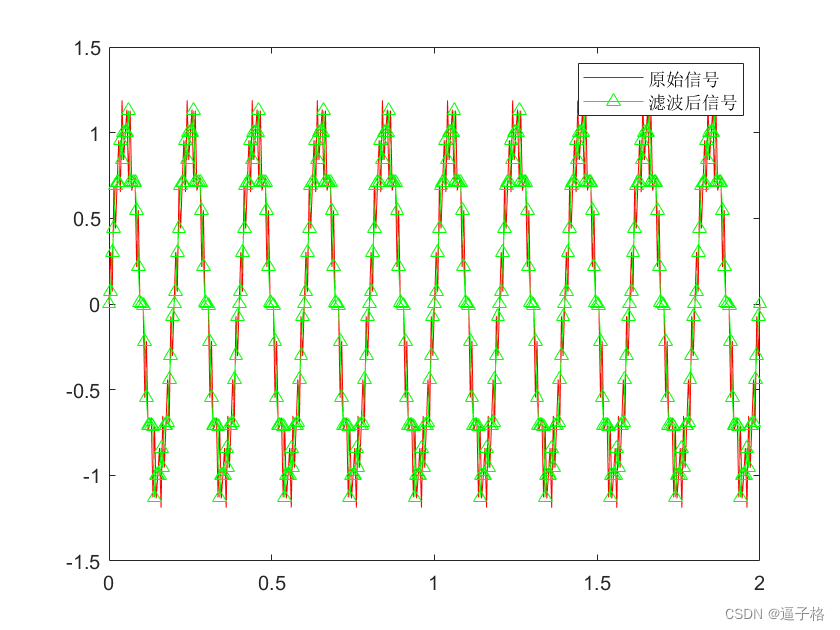
fs = 200;%频率
t = 0:1/fs:2;
x = sin(2*pi*t*5)+0.25*sin(2*pi*t*80);
y = medfilt1(x,3);
plot(t,x,'-','color','r')
hold on;
plot(t,y,'-^','color','g')
legend('原始信号','滤波后信号')视图效果
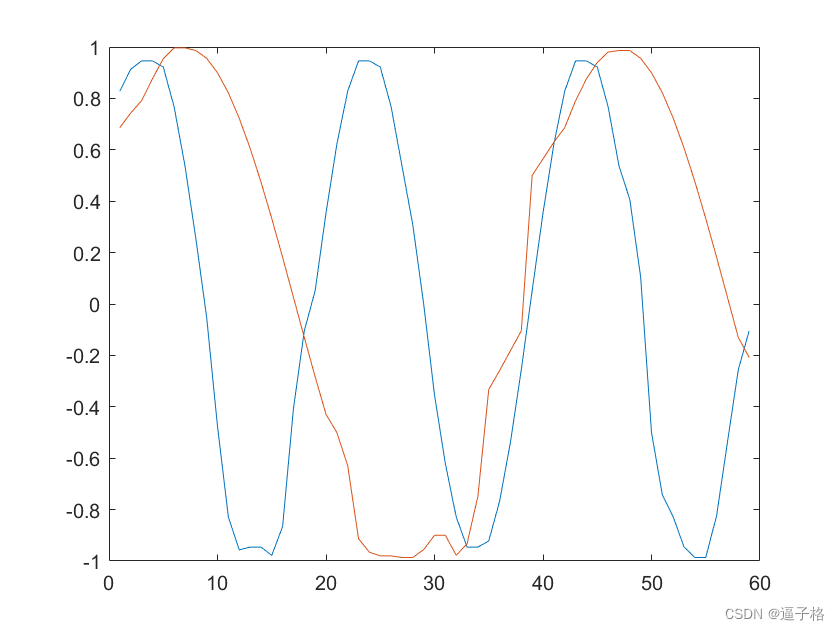
2)带有尖峰和丢失样本的多通道信号中值滤波
说明:
生成一个由不同频率正弦波组成的双通道信号。在随机位置加入尖峰。在随机位置用NaN添加缺失样本。重置随机数生成器设置加入噪声位置。
多通道信号生成代码
Matlab
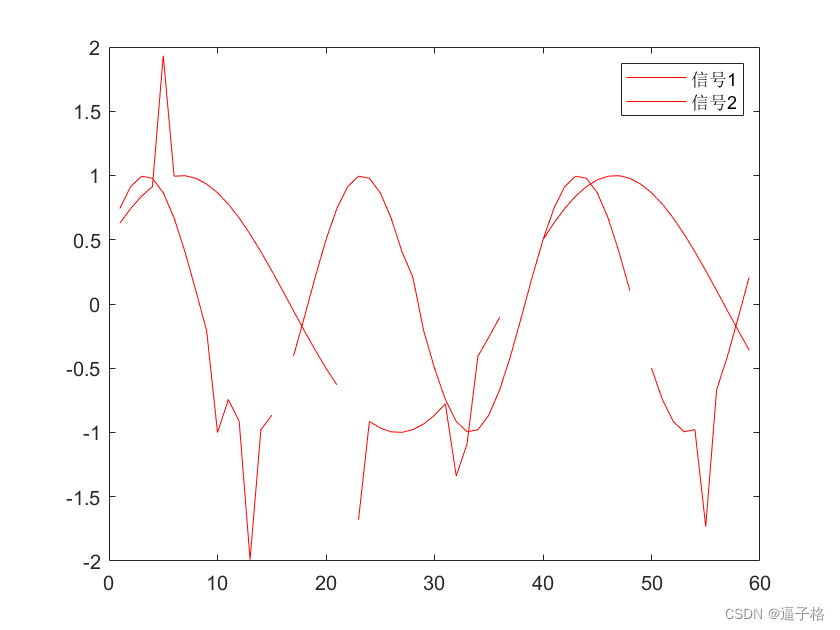
rng('default')
n = 59;
x = sin(pi./[10 20]'*(1:n)+pi/6)';
spk = randi(100,9,1);
x(spk) = x(spk)*2;
x(randi(100,6,1)) = NaN;
plot(x,'color','r')
legend('信号1','信号2')试图效果
中值滤波效果对比
代码
Matlab
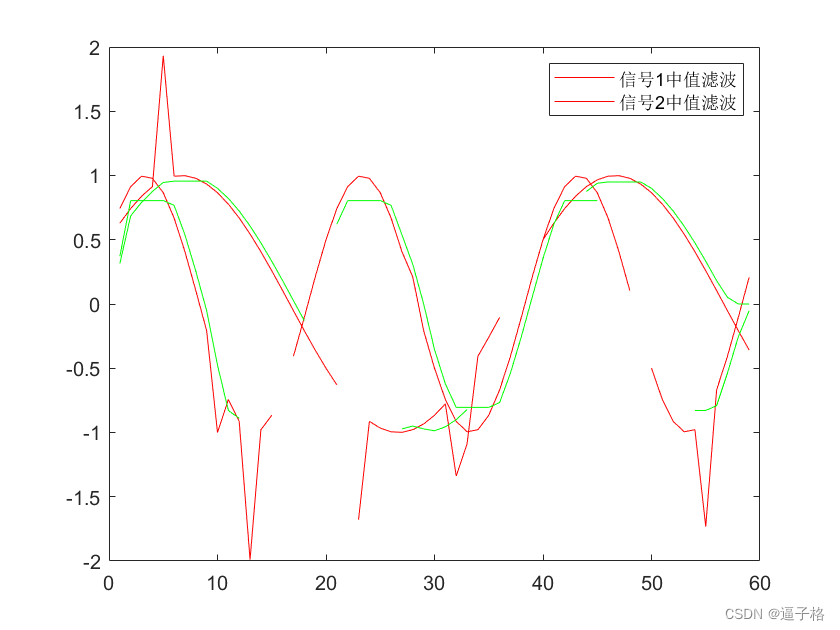
rng('default')
n = 59;
x = sin(pi./[10 20]'*(1:n)+pi/6)';
spk = randi(100,9,1);
x(spk) = x(spk)*2;
x(randi(100,6,1)) = NaN;
plot(x,'color','r')
legend('信号1','信号2')
hold on;
y = medfilt1(x,8);
plot(y,'color','g')
legend('信号1中值滤波','信号2中值滤波')试图效果
信号缺失部分处理(NaN)
代码
Matlab
y = medfilt1(x,4,'omitnan');
plot(y)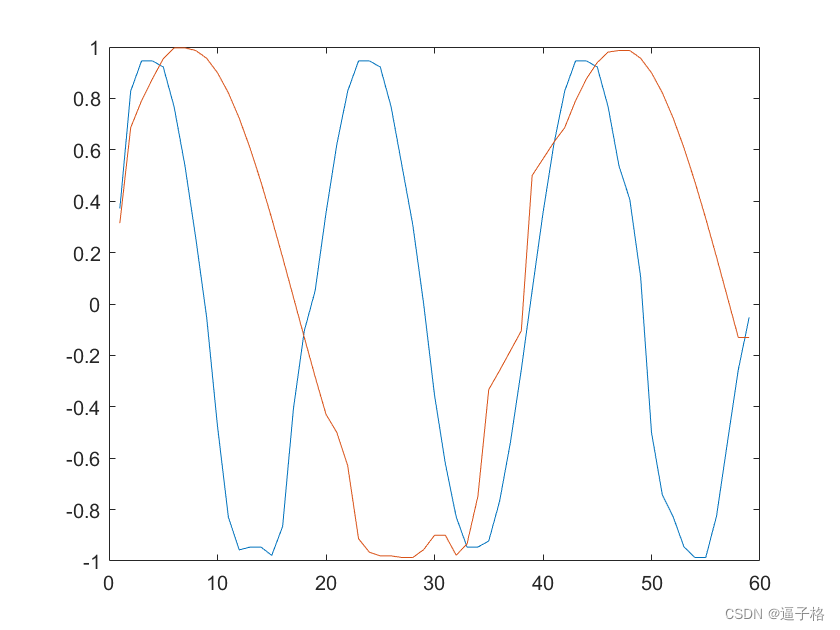
边缘滤波
代码
Matlab
y = medfilt1(x,4,'omitnan','truncate');
plot(y)视图效果
4、 萨维茨基-戈雷滤波滤波器:sgolayfilt()
说明:萨维茨基-戈雷滤波
语法
语法1:y = sgolayfilt(x,order,framelen) 对向量 x 中的数据应用多项式阶数为 order、帧长度为
framelen 的萨维茨基-戈雷有限冲激响应 (FIR) 平滑滤波器。
语法2:y = sgolayfilt(x,order,framelen,weights) 指定在最小二乘最小化过程中要使用的加权向量。
语法3:y = sgolayfilt(x,order,framelen,weights,dim) 指定滤波器沿其运算的维度。
参数
x:输入信号 order:多项式阶数 framelen:帧长度 weights:加权数组 dim:要沿其滤波的维度
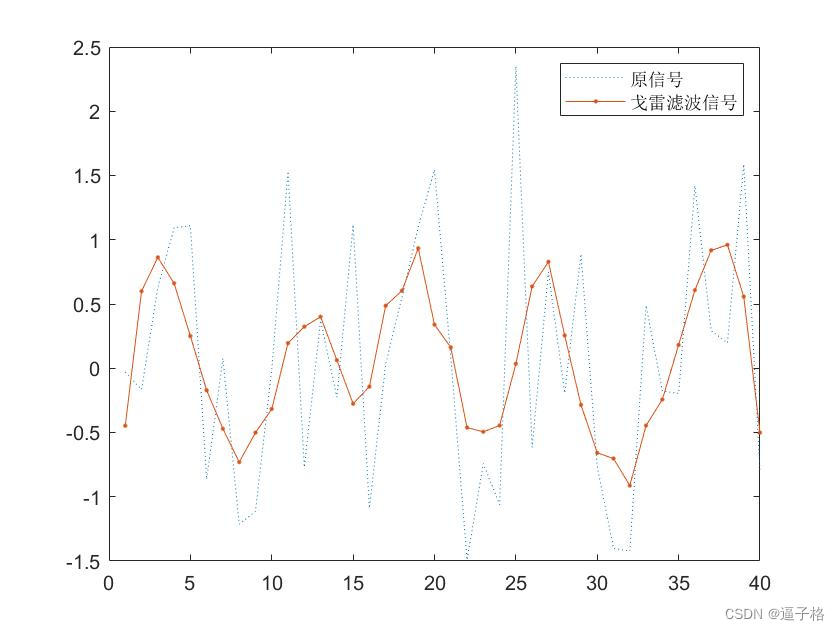
1)稳态和瞬变萨维茨基-戈雷滤波器
萨维茨基-戈雷滤波器滤波代码
Matlab
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
legend('原信号','戈雷滤波信号')
hold on视图效果
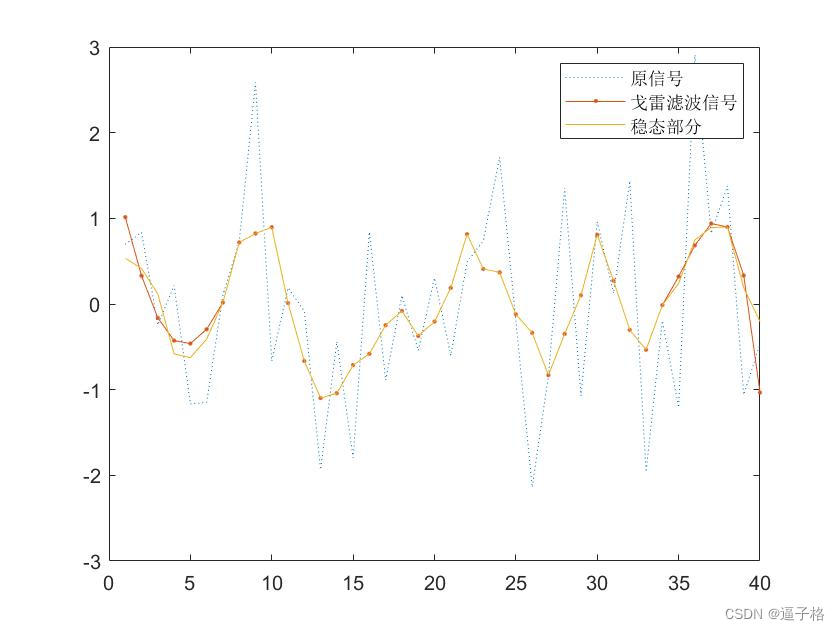
2) 稳态萨维茨基-戈雷滤波器滤波代码
Matlab
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
% legend('原信号','戈雷滤波信号')
hold on
m = (framelen-1)/2;
B = sgolay(order,framelen);
steady = conv(x,B(m+1,:),'same');%原信号与过滤信号卷积滤波 得到稳态部分
plot(steady)
legend('原信号','戈雷滤波信号','稳态部分')视图效果
3)启动瞬态和终止瞬态代码
Matlab
order = 4;%参数设置 可以根据需求设置
framelen = 13;
l = 40;
x = randn(l,1);
sgf = sgolayfilt(x,order,framelen);
plot(x,':')
hold on
plot(sgf,'.-')
% legend('原信号','戈雷滤波信号')
hold on
m = (framelen-1)/2;
B = sgolay(order,framelen);
steady = conv(x,B(m+1,:),'same');%原信号与过滤信号卷积滤波 得到稳态部分
plot(steady)
legend('原信号','戈雷滤波信号','稳态部分')
ybeg = B(1:m,:)*x(1:framelen);%启动瞬态
yend = B(framelen-m+1:framelen,:)*x(l-framelen+1:l);%终止瞬态
cmplt = steady;
cmplt(1:m) = ybeg;
cmplt(l-m+1:l) = yend;
plot(cmplt)
legend('原信号','戈雷滤波信号','稳态部分','完整信号')视图效果

5、总结
中值滤波和萨维茨基-戈雷滤波是两种常用的图像滤波技术,用于去除图像中的噪声并改善图像质量。以下是它们的一些特点和总结:
- 中值滤波:
- 中值滤波适用于去除椒盐噪声和斑点噪声,能够有效地保留图像的边缘信息。
- 中值滤波原理是取邻域内像素值的中值作为中心像素的值,因此对于异常像素值的影响较小。
- 在MATLAB中,可以使用medfilt2函数实现中值滤波,通过调整滤波窗口大小来控制滤波效果。
- 萨维茨基-戈雷滤波:
- 萨维茨基-戈雷滤波是一种综合了均值滤波和中值滤波的滤波方法,能够在去除噪声的同时保持图像细节。
- 萨维茨基-戈雷滤波根据窗口内像素值的方差来调整滤波权重,适用于不同类型的噪声。
- 在MATLAB中,可以利用wiener2函数实现萨维茨基-戈雷滤波,同样可以通过调整窗口大小等参数来优化滤波效果。
总的来说,中值滤波适合去除椒盐噪声和斑点噪声,而萨维茨基-戈雷滤波则可以在去噪的同时保持图像的细节信息。根据实际应用需求和图像特点,可以选择合适的滤波方法来提升图像质量。