哈喽GPT-4o，对GPT-4o 数据分析Data Analysis的思考与看法

- [上传一个Excel给Data Analysis。](#上传一个Excel给Data Analysis。)
- 绘制分形图形
- - Prompt：你能够绘制朱利亚集合吗？请以合适的方式展示出来
- 计算复杂的数学问题
- - [Prompt：请画出这个函数的图像：x^3^ + y^3^ = 3axy，a 的值从 -10 到 10。](#Prompt：请画出这个函数的图像：x^3^ + y^3^ = 3axy，a 的值从 -10 到 10。)
- [使用Data Analysis做一道高数题](#使用Data Analysis做一道高数题)
- - [Prompt：计算由摆线 x = a(t - sin t), y = a(1 - cos t) 相应于 0 ≤ t ≤ 2π 的一拱与直线 y = 0 所围成的图形绕 x 轴旋转而成的旋转体体积。要保证计算过程和结果都要正确。](#Prompt：计算由摆线 x = a(t - sin t), y = a(1 - cos t) 相应于 0 ≤ t ≤ 2π 的一拱与直线 y = 0 所围成的图形绕 x 轴旋转而成的旋转体体积。要保证计算过程和结果都要正确。)

大家好，我是哪吒。

OpenAI的GPT-4o的横空出世，再次巩固了其作为行业颠覆者的地位。GPT-4o的发布不仅仅是一个产品的揭晓，它更像是向世界宣告AI技术已迈入了一个全新的纪元，连OpenAI的领航者萨姆·奥特曼也不禁感慨，这如同直接从科幻电影情节走进现实。

GPT-4o以及ChatGPT产品的快速总结：图片GPT-4o（"o"代表"全能"）它可以接受任意组合的文本、音频和图像作为输入，并生成任意组合的文本、音频和图像输出。

GPT-4o的问世，标志着AI技术的一个巨大飞跃，它不再局限于单一媒介的交互，而是开创性地实现了文本、语音、图像三者间的无缝融合。

👉 GPT功能：

GPT-4o知识问答：支持1000+token上下文记忆功能
最强代码大模型Code Copilot：代码自动补全、代码优化建议、代码重构等
DALL-E AI绘画：AI绘画 + 剪辑 = 自媒体新时代
私信哪吒，直接使用GPT-4o

新模型新玩法，下面简单介绍一下 GPT-4o 数据分析插件Data Analysis~

Data Analysis 提供了丰富的工具和库来支持这些任务，使其成为数据分析的强大环境。

无论是数据科学分析新手还是专家，都可以按步骤进行实践，了解如何使用Data Analysis进行数据加载、清洗、探索和可视化。

上传一个Excel给Data Analysis。

Prompt：请问这个数据集是做什么的

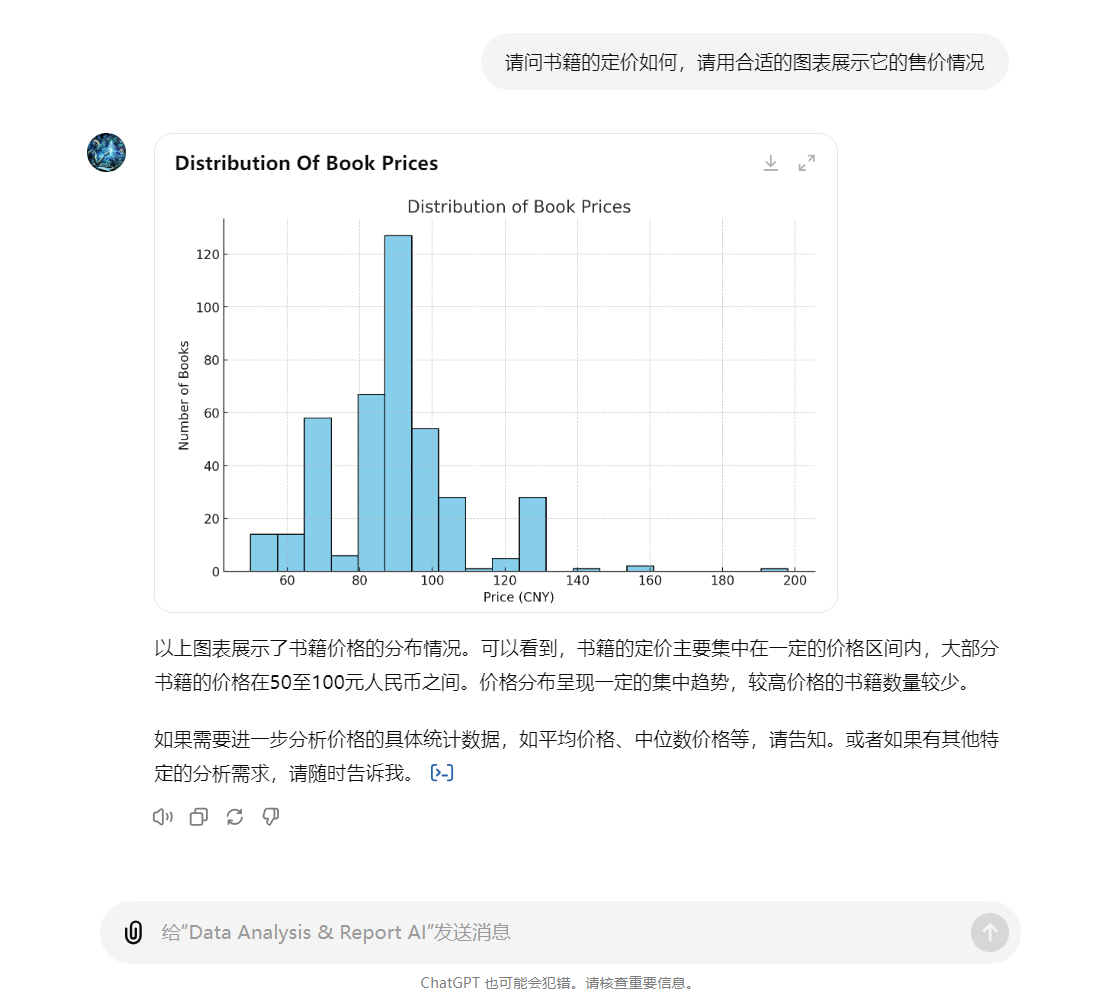
Prompt：请问书籍的定价如何，请用合适的图表展示它的售价情况

Prompt：请统计书名列中出现最多的名称，然后使用词云将其可视化。

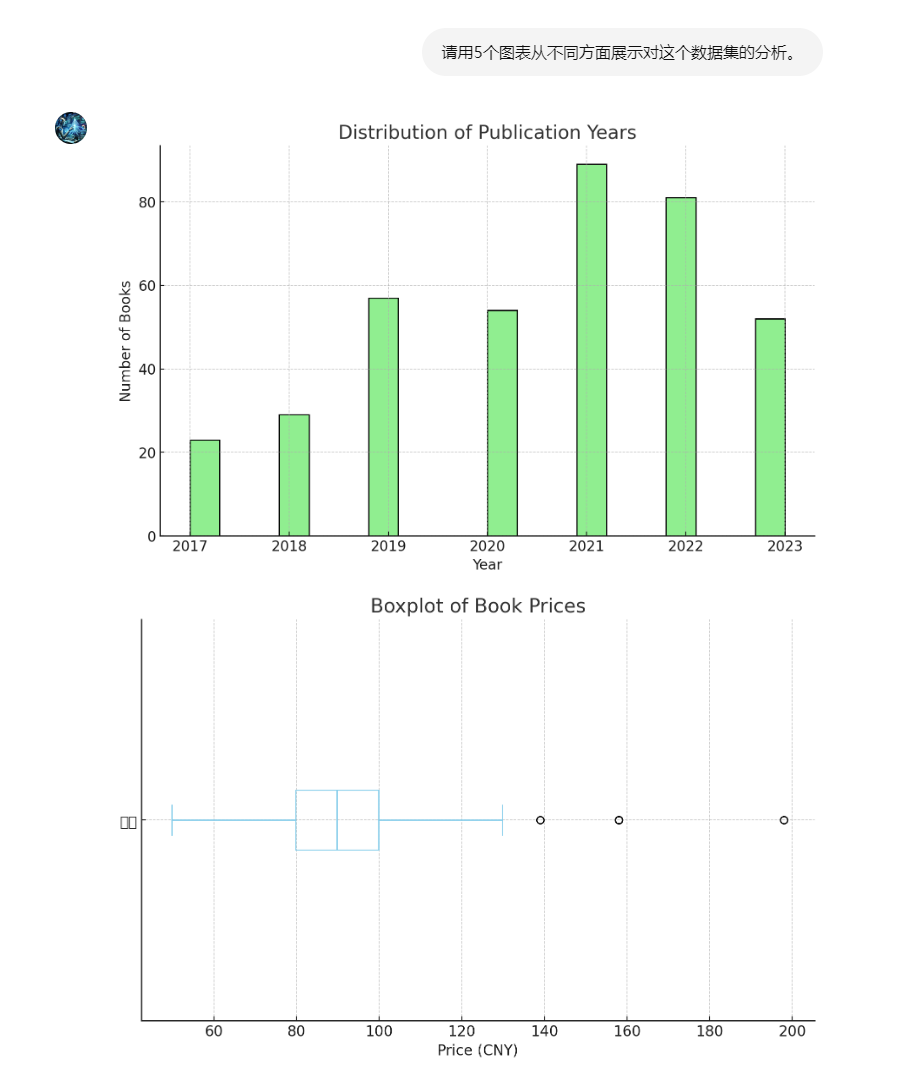
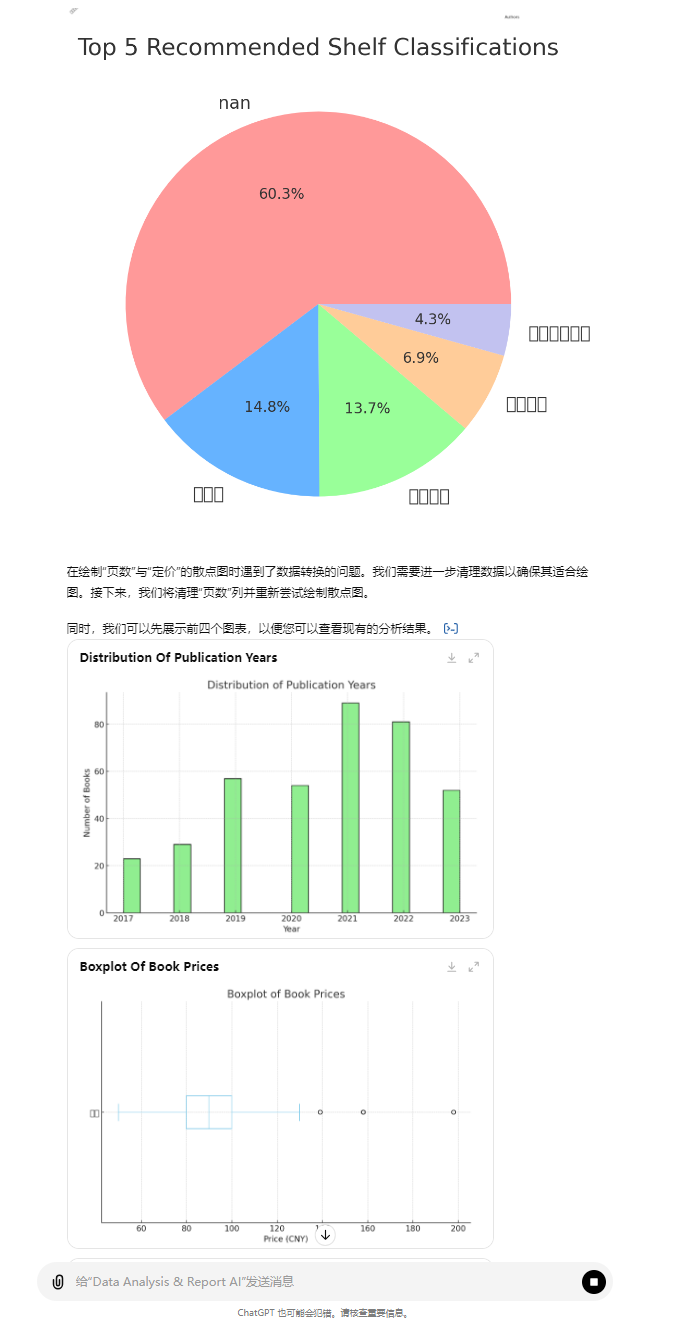
Prompt：请用5个图表从不同方面展示对这个数据集的分析。

绘制分形图形

分形图形是一类由相似部分构成的复杂结构，每个部分都是整体的缩小版。分形的独特之处在于其复杂的结构在不同尺度上重复出现，因此无论将图像放大或缩小，都能看到相同的基本形状。这一特性称为自相似性。

分形是数学和自然界中常见的现象，可以用数学方程来描述。以下是一些经典的分形图形：

(1) 曼德布罗特集合（Mandelbrot Set）：分形中最著名的例子之一，由复杂的数学方程定义，并在复数平面上展示。

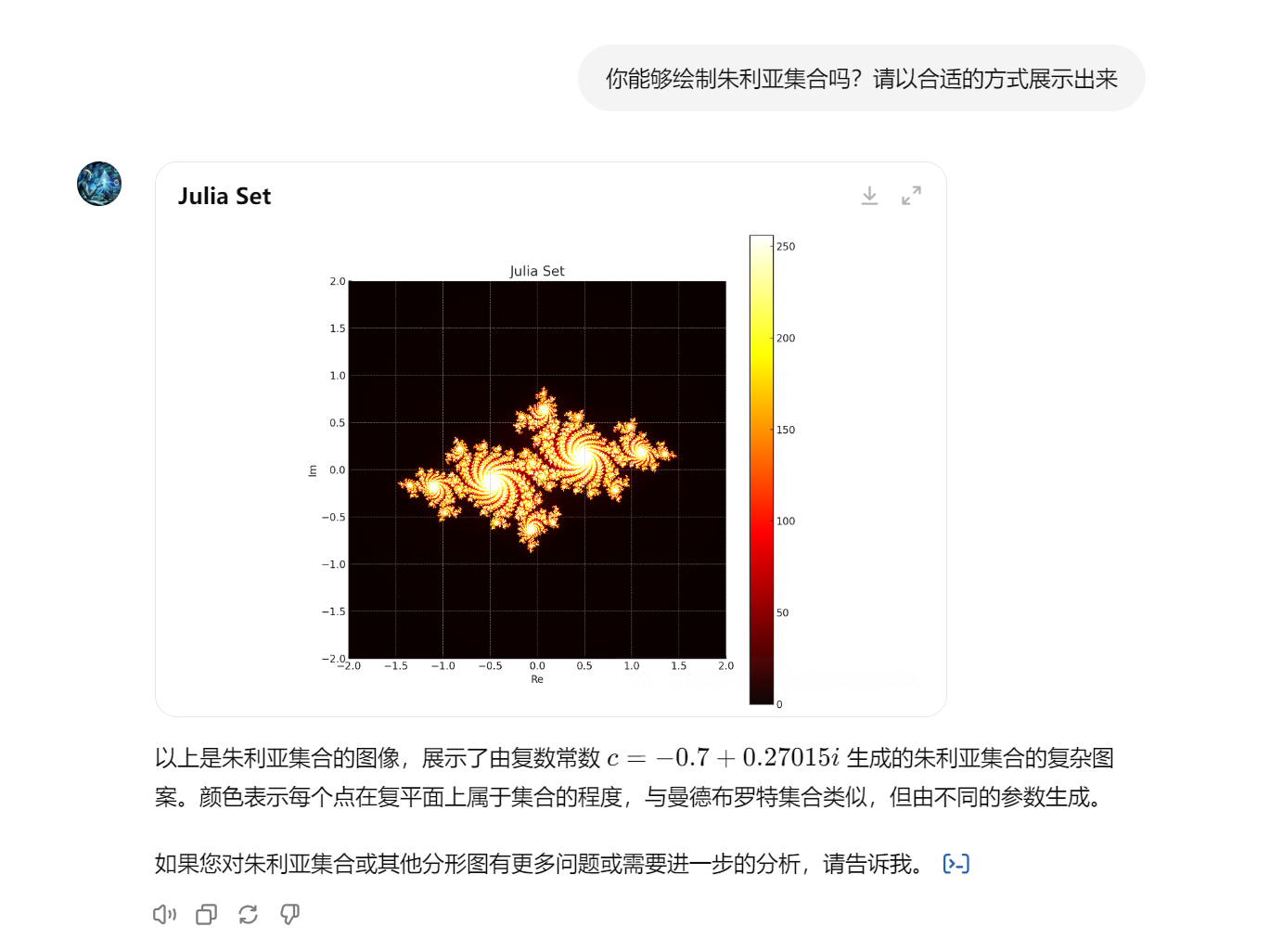
(2) 朱利亚集合（Julia Set）：与曼德布罗特集合相关，但每个点的行为有所不同。

(3) 谢尔宾斯基三角形（Sierpinski Triangle）：一个简单但引人注目的分形，由不断缩小的三角形组成。

(4) 科赫曲线（Koch Curve）：一个无限复杂的连续分形，由反复添加新的几何形状构成。

分形不仅在数学中有趣，也在自然界中广泛存在。例如，在云朵、山脉、河流、树木等中都可以观察到分形结构。

此外，分形在艺术和计算机图形学中也有广泛应用。它们可用于创建复杂而美丽的图案，常见于电影和视频游戏中的自然景观建模。

分形的研究不仅加深了我们对数学和自然界复杂性的理解，还推动了多个领域的技术进步。

下面使用Data Analysis绘制分形图形。

Prompt：你能够绘制朱利亚集合吗？请以合适的方式展示出来

计算复杂的数学问题

Data Analysis 的数学计算过程本质上是通过 Python 程序调用 SymPy 库等专业工具来实现的。SymPy 库不仅支持符号计算和高精度计算，还具备模式匹配、绘图、解方程、微积分、组合数学、离散数学、几何学、概率与统计及物理学等多方面的功能。借助 Data Analysis，用户可以解决大量基础数学问题，展现其强大和灵活的计算能力。

Prompt：请画出这个函数的图像：x^3^ + y^3^ = 3axy，a 的值从 -10 到 10。

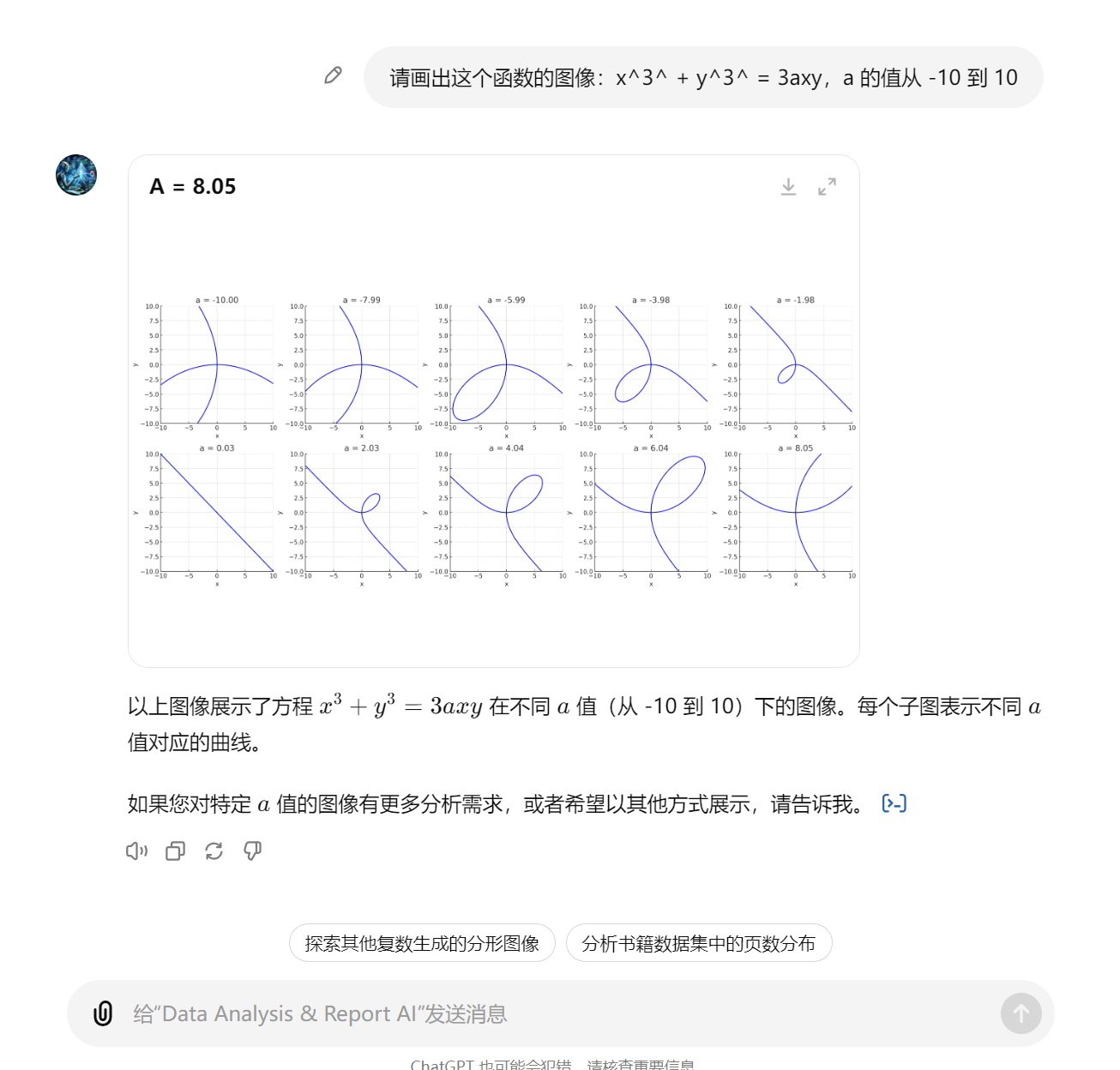
使用Data Analysis做一道高数题

Prompt：计算由摆线 x = a(t - sin t), y = a(1 - cos t) 相应于 0 ≤ t ≤ 2π 的一拱与直线 y = 0 所围成的图形绕 x 轴旋转而成的旋转体体积。要保证计算过程和结果都要正确。

在处理较为复杂的数学问题时，Data Analysis 有时会显示出其局限性。Wolfram Alpha 的首席科学家 Michael Trott 为了展示不同工具在解决数学难题方面的效果，特意挑选了一百道数学问题，这些问题来源广泛，包括数学杂志、大学数学竞赛和数学奥林匹克等。随后，他分别利用 Wolfram Plugin 和 Data Analysis 进行尝试，以应对这些挑战性的问题。

实验结果表明，Wolfram Plugin 凭借其强大的计算能力解决了全部问题，而 Data Analysis 仅解决了约 50% 的问题。这个结果清楚地表明，Wolfram Plugin 在处理复杂数学问题时具有显著优势。

此外，他还比较了两者在解决问题时所需的代码长度。值得注意的是，使用 Wolfram 语言编写的代码长度仅为 Data Analysis 使用 Python 代码长度的 27%。这一结果进一步验证了 Wolfram 语言在编写效率和代码简洁性方面的卓越性。

因此，尽管 Data Analysis 在许多方面表现优异，但在解决复杂数学问题时，仍然推荐使用 Wolfram Plugin。这不仅能提供更准确和全面的解决方案，还能通过更简洁的代码节省时间和精力。