探秘神经网络激活函数：Sigmoid、Tanh和ReLU，解析非线性激活函数的神奇之处

引言

在神经网络中，激活函数扮演着至关重要的角色。它们赋予神经网络非线性的能力，使得网络具备学习和表示复杂函数关系的能力。本文将详细解析三种常见的激活函数：Sigmoid、Tanh和ReLU，揭开它们在神经网络中的奥秘。无论你是初学者还是有一定经验的深度学习从业者，本文都将带你深入了解这些激活函数的原理、特点和应用，为你的神经网络之旅增添新的惊喜！

第一部分：Sigmoid函数

在神经网络中，Sigmoid函数是最早被广泛使用的激活函数之一。它的数学定义如下：

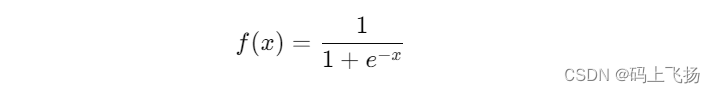
Sigmoid函数的主要特点是将输入值映射到一个介于0和1之间的输出值。它的曲线形状类似于一个"S"型，因此也被称为逻辑函数。Sigmoid函数在神经网络中的应用非常广泛，特别是在二分类问题和输出层的概率预测中常被使用。

1. 特点和优点

Sigmoid函数具有以下特点和优点：

1. 输出范围限制：Sigmoid函数的输出范围在0到1之间，可以被看作是一个概率值，用于表示某个事件发生的概率。
2. 平滑连续：Sigmoid函数是一个平滑连续的函数，具有良好的可微性，有利于梯度的计算和反向传播。
3. 非线性：Sigmoid函数引入了非线性，使得神经网络可以学习和表示复杂的非线性函数关系。

2. 问题和限制

然而，Sigmoid函数也存在一些问题和限制：

1. 梯度消失：在Sigmoid函数的两端，梯度接近于0，导致反向传播时梯度逐渐消失。这使得深层网络的训练变得困难，限制了网络的深度和性能。
2. 输出非均衡：当输入值较大或较小时，Sigmoid函数的输出接近于0或1，导致输出值分布不均衡，这可能会影响模型的收敛速度和性能。
3. 计算开销：相比于其他激活函数，Sigmoid函数的计算开销较大，涉及指数运算，对于大规模数据和深层网络可能会影响计算效率。

3. 应用场景

尽管Sigmoid函数存在一些问题，但它仍然在某些场景下有着广泛的应用，特别是在二分类问题和输出层的概率预测中常被使用。以下是一些适合使用Sigmoid函数的应用场景：

1. 二分类问题：Sigmoid函数可以将输出值映射到0和1之间，用于表示某个事件发生的概率，因此适用于二分类问题，如判断图像中是否包含某个目标。
2. 输出层概率预测：在输出层中，Sigmoid函数可以用于预测概率分布，如多类别分类中各类别的概率。
3. 逻辑回归：Sigmoid函数在逻辑回归中被广泛应用，用于建模和预测二分类问题。

Sigmoid函数是一种常见的激活函数，具有将输入值映射到0和1之间的特点。它在二分类问题和输出层概率预测中有广泛的应用。然而，由于其存在的问题和限制，近年来它的使用已经逐渐减少，被更优秀的激活函数如ReLU所取代。在选择激活函数时，需要根据具体问题和网络结构的要求进行权衡和选择。

第二部分：Tanh函数

Tanh函数，全称为双曲正切函数（Hyperbolic Tangent Function），是Sigmoid函数的一种变体。它将输入值映射到一个介于-1和1之间的输出值，相对于Sigmoid函数的[0, 1]输出范围，Tanh函数的输出范围更大，且具有对称性。Tanh函数在神经网络中具有独特的优势和广泛的应用。

1. 数学定义和直观理解

Tanh函数的数学定义如下：

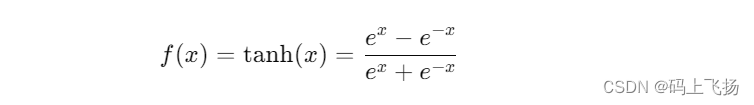
从公式可以看出，Tanh函数的值范围在-1到1之间。与Sigmoid函数类似，当输入值趋向于正无穷大时，Tanh函数的输出值接近于1；当输入值趋向于负无穷大时，输出值接近于-1；当输入值为0时，输出值为0。

2. 特点和优点

Tanh函数具有以下特点和优点：

1. 输出范围和对称性：Tanh函数的输出范围在-1到1之间，相对于Sigmoid函数[-0.5, 0.5]的输出，Tanh函数的输出范围更大，有利于数据的归一化和处理。此外，Tanh函数是对称的，这意味着它的输出在0点上下对称，有利于中心化数据处理。

2. 平滑性和可微性：Tanh函数是一个平滑的连续函数，具有良好的可微性，这对于神经网络的训练非常重要，特别是在使用反向传播算法时。

3. 梯度消失问题的缓解：虽然Tanh函数仍然存在梯度消失问题，但由于其输出范围在-1到1之间，且在0附近梯度较大，相比于Sigmoid函数，Tanh函数在缓解梯度消失问题上有所改善。

3. 问题和限制

尽管Tanh函数具有许多优点，但它也存在一些问题和限制：

1. 梯度消失问题：在输入值非常大或非常小时，Tanh函数的梯度仍然会趋近于0，导致梯度消失问题，影响深层神经网络的训练效果。

2. 计算开销：与ReLU函数相比，Tanh函数的计算开销更大，因为它涉及指数运算。这在大规模数据和深层网络中可能会影响计算效率。

4. 应用场景

Tanh函数广泛应用于各种神经网络中，特别是在处理归一化数据和需要对称输出的场景中。以下是一些适合使用Tanh函数的应用场景：

1. 自然语言处理：在自然语言处理任务中，如情感分析、机器翻译等，Tanh函数常用于处理归一化数据，帮助模型更好地捕捉数据的特征和模式。

2. 回归问题：在一些回归问题中，Tanh函数可以将输入值映射到一个对称的范围，使得输出更加平滑和稳定。

3. 隐藏层激活函数：在多层感知器（MLP）和卷积神经网络（CNN）等网络结构中，Tanh函数常用作隐藏层的激活函数，以增强模型的非线性表达能力。

Tanh函数是一种常见的激活函数，具有将输入值映射到-1和1之间的特点。它在处理归一化数据和需要对称输出的场景中表现出色。尽管Tanh函数存在梯度消失和计算开销的问题，但它在许多神经网络应用中仍然广泛使用。通过了解Tanh函数的特点和应用场景，开发者可以在构建神经网络时更好地选择和使用适合的激活函数，从而提高模型的性能和稳定性。

第三部分：ReLU函数

ReLU函数，全称为修正线性单元函数（Rectified Linear Unit），是一种常用的激活函数，在深度学习和神经网络中被广泛应用。相比于Sigmoid函数和Tanh函数，ReLU函数具有简单的计算和优秀的性能表现，因此成为了许多神经网络的首选激活函数。

1. 数学定义和直观理解

ReLU函数的数学定义如下：

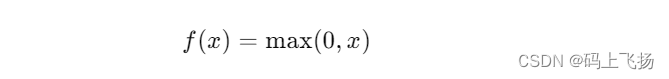
从定义可以看出，当输入值𝑥x大于0时，ReLU函数的输出值等于输入值𝑥x；当输入值𝑥x小于等于0时，ReLU函数的输出值为0。换句话说，ReLU函数对于正数输入直接输出，对于负数输入则输出0。

2. 特点和优点

ReLU函数具有以下特点和优点：

1. 线性关系：ReLU函数在输入大于0时是线性的，这使得它在模型的训练和优化过程中更易于处理。

2. 解决梯度消失问题：相比于Sigmoid函数和Tanh函数，ReLU函数在正区间上具有常数梯度。这意味着在反向传播过程中，梯度不会出现过度衰减的问题，从而避免梯度消失问题，有助于提高深层神经网络的训练效果。

3. 稀疏激活性：由于ReLU函数在负区间上的输出为0，它具有稀疏激活性，即只有部分神经元会被激活。这种稀疏性有助于减少模型的复杂性和计算开销，并且可以提高模型的泛化能力。

4. 计算效率：ReLU函数的计算非常简单，只需要比较输入值和0的大小，因此在计算效率方面具有优势。这对于大规模数据和深层网络的训练和推断非常重要。

3. 问题和限制

尽管ReLU函数具有很多优点，但它也存在一些问题和限制：

1. Dead ReLU问题：当输入值小于等于0时，ReLU函数的输出为0，这可能导致神经元进入"死亡"状态，即无论输入值如何变化，梯度始终为0，无法更新权重。这个问题在训练过程中可能会出现，需要注意。

2. 不具备负值输出：ReLU函数在负区间上的输出恒为0，这可能导致一些信息的丢失。对于一些任务和数据，负值的表示能力可能是有意义的，因此ReLU函数在这些情况下可能不适用。

4. 应用场景

ReLU函数广泛应用于各种神经网络和深度学习模型中。以下是一些适合使用ReLU函数的应用场景：

1. 卷积神经网络（CNN）：ReLU函数在卷积层中常被用作激活函数，用于提取图像和特征的非线性表示。

2. 深度神经网络：ReLU函数在深度神经网络的隐藏层中具有良好的性能和训练效果，对于解决各种复杂任务和数据集非常有效。

3. 稀疏表示和特征选择：ReLU函数的稀疏激活性可以帮助实现稀疏表示和特征选择，对于处理高维数据和降低模型复杂度非常有帮助。

ReLU函数是一种简单而有效的激活函数，具有线性关系、解决梯度消失问题、稀疏激活性和计算效率等优点。它在深度学习和神经网络中被广泛使用，并在各种应用场景中取得了良好的性能和结果。了解ReLU函数的特点和适用场景，可以帮助开发者更好地选择和使用激活函数，提高模型的表达能力和训练效果。

第四部分：激活函数的选择和应用建议

选择合适的激活函数对于神经网络的性能和训练效果至关重要。在实际应用中，开发者需要根据具体任务和数据的特点来选择适合的激活函数。本部分将提供一些建议和指导，帮助开发者在选择和应用激活函数时做出明智的决策。

1. 考虑任务类型

首先，开发者应该考虑任务的类型和需求。不同的任务可能对激活函数有不同的要求。例如：

• 二分类问题：对于二分类问题，Sigmoid函数和ReLU函数都是常见的选择。Sigmoid函数可以将输出限制在[0, 1]之间，适用于输出概率值。而ReLU函数则可以提供更好的非线性表达能力。

• 多分类问题：对于多分类问题，通常使用Softmax函数作为输出层的激活函数，可以将输出转化为类别的概率分布。

• 回归问题：对于回归问题，Tanh函数和ReLU函数都是常用的选择。Tanh函数可以将输出限制在[-1, 1]之间，适合处理归一化数据。ReLU函数则可以提供更好的线性关系和非线性表达能力。

2. 考虑网络结构

网络结构也是选择激活函数的重要因素。不同的神经网络结构对激活函数的要求有所不同。以下是一些常见的网络结构和对应的激活函数选择建议：

• 多层感知器（MLP）：对于MLP网络，Tanh函数和ReLU函数是常用的选择。Tanh函数可以提供对称性和平滑性，适合处理归一化数据。ReLU函数则可以提供更好的非线性表达能力。

• 卷积神经网络（CNN）：对于CNN网络，ReLU函数是最常用的选择，特别是在卷积层中。ReLU函数具有线性关系和稀疏激活性，适合提取图像和特征的非线性表示。

• 循环神经网络（RNN）：对于RNN网络，常用的激活函数包括Tanh函数和ReLU函数。Tanh函数可以提供平滑性和对称性，适合处理序列数据。ReLU函数则可以提供更好的非线性表达能力，适合处理长期依赖关系。

3. 考虑梯度消失和爆炸问题

梯度消失和梯度爆炸是训练深度神经网络时常遇到的问题。选择合适的激活函数可以缓解这些问题。以下是一些建议：

• 梯度消失问题：如果模型在训练过程中出现梯度消失问题，可以考虑使用ReLU函数或其变种（如Leaky ReLU、PReLU等）。这些函数在正区间上具有常数梯度，有助于传播梯度并避免梯度过度衰减。

• 梯度爆炸问题：如果模型在训练过程中出现梯度爆炸问题，可以考虑使用梯度剪裁（Gradient Clipping）等技术来限制梯度的大小。此外，可以使用Tanh函数等具有较小输出范围的激活函数，有助于控制梯度的大小。

4. 考虑计算效率和模型复杂度

最后，开发者还应该考虑激活函数的计算效率和模型复杂度。一些激活函数具有简单的计算形式，可以提高模型的训练和推断效率。另外，一些稀疏激活函数可以帮助减少模型的复杂性和计算开销。

总之，在选择和应用激活函数时，开发者应该考虑任务类型、网络结构、梯度消失和爆炸问题，以及计算效率和模型复杂度等因素。根据具体情况，选择合适的激活函数可以提高模型的表达能力、训练效果和计算效率。同时，不同激活函数的组合和变种也值得尝试，以进一步优化神经网络的性能。

结论

通过本文的解读，你将深入了解Sigmoid、Tanh和ReLU函数这三种常见的激活函数。你将理解它们的数学定义、特点和应用场景，并掌握在实际应用中选择和使用激活函数的技巧。无论你是初学者还是有一定经验的从业者，本文都将为你在神经网络中应用合适的激活函数提供指导，让你的模型更加强大和高效。