5,梯度下降优化器
5,1 梯度下降在深度学习中的作用
在深度学习中,权重W的值是否合理是由损失函数L来判断的。L越小,表示W的设置越happy。L越大,表示W的值越unhappy。 为了让L越来越小,常用的方法是梯度下降法。

5,2 梯度下降法的基本原理
梯度下降法的原理是基于函数f在点P处的梯度一定是函数f在P点处的所有方向导数中增加最大的方向导数。 因此,只要**沿着梯度方向移动自变量 x,函数值 f 就会以最快的速度增加。要想让x沿着梯度方向移动,只需让自变量x加上梯度。**且,不论梯度是正还是负,函数值f都会增加。
对梯度下降法而言,则正好相反。我们希望尽快找到函数的最小值,以及此时的自变量x。 因此,我们应该让自变量x不断地朝着梯度的反方向移动,这样函数值就会很快减小。而让x沿着梯度的反方向移动的方法,则是让x减去梯度。
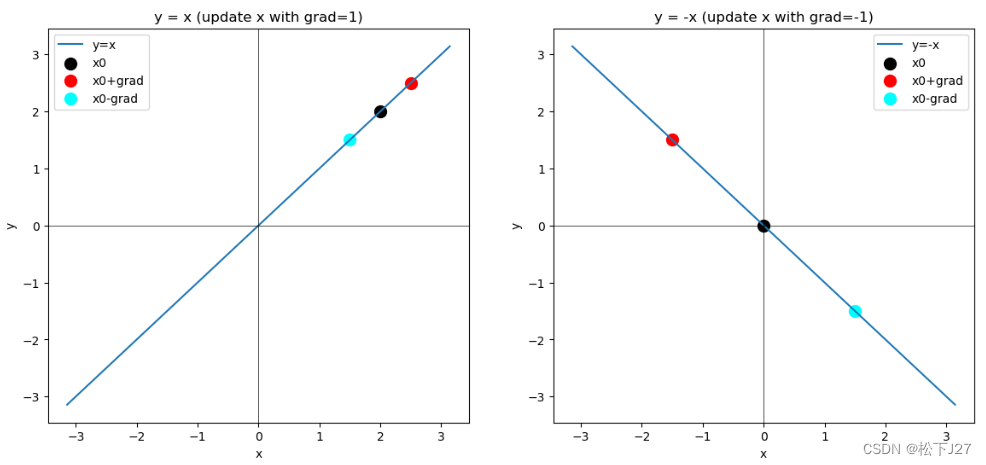
以一元一次函数y=x和y=-x为例:
图中x0表示自变量x的初始位置,红点表示x0加梯度后的坐标,蓝点表示x0减去梯度后的位置。对函数y=x而言,梯度为正1,x0=2加上梯度后会朝着x轴的正向移动,函数值增加。对函数y=-x而言,梯度为负1,x0=0加上梯度后会朝着x轴的反方向移动,函数值还是在增加。
对梯度下降法而言,则是希望把x0朝着蓝点方向移动。对于两幅图中的两个函数,我同时让x0减去梯度,得到了图中的蓝点。如果继续移动,则函数值会越来越低,直到函数的最小值。
python
import numpy as np
import matplotlib.pyplot as plt
#y=x
def f(x):
return x
def df(x):
return 1
#y=-x
def ff(x):
return -x
def dff(x):
return -1
x=np.linspace(-np.pi,np.pi,300)
#画y=x
fig,axs=plt.subplots(1,2, figsize=(14, 6))
y=f(x)
axs[0].plot(x,y,label='y=x')
axs[0].set_title('y = x (update x with grad=1)')
axs[0].set_xlabel('x')
axs[0].set_ylabel('y')
axs[0].axhline(0, color='black', linewidth=0.5)
axs[0].axvline(0, color='black', linewidth=0.5)
#当前x的位置
x0=2
axs[0].scatter(x0,f(x0),color='black', s=100,label='x0')
#沿着函数增加的方向移动x(移动lr个单位的梯度)
#注意我这里是用自变量加梯度
lr=0.5
x1=x0+lr*df(x0)
x2=x0-lr*df(x0)
axs[0].scatter(x1,f(x1),color='red', s=100,label='x0+grad')
axs[0].scatter(x2,f(x2),color='cyan', s=100,label='x0-grad')
axs[0].legend()
#画y=-x
y=ff(x)
axs[1].plot(x,y,label='y=-x')
axs[1].set_title('y = -x (update x with grad=-1)')
axs[1].set_xlabel('x')
axs[1].set_ylabel('y')
axs[1].axhline(0, color='black', linewidth=0.5)
axs[1].axvline(0, color='black', linewidth=0.5)
#当前x的位置
x0=0
axs[1].scatter(x0,ff(x0),color='black', s=100,label='x0')
#沿着函数增加的方向移动x(移动lr个单位的梯度)
#注意我这里依然是用自变量加梯度
lr=1.5
x1=x0+lr*dff(x0)
x2=x0-lr*dff(x0)
axs[1].scatter(x1,ff(x1),color='red', s=100,label='x0+grad')
axs[1].scatter(x2,ff(x2),color='cyan', s=100,label='x0-grad')
axs[1].legend()如果要以深度学习的损失函数为例,下图中权重W为自变量,损失函数L(x,W)所对应的梯度如下图中Grad(L(x,W))所示。现在,为了让目标函数L(损失函数)的值迅速减小,就要让自变量W沿着梯度的反方向移动 。这样一来,损失函数L的函数值就会迅速减小。即,通过改变自变量W的值,使得函数L的值小于当前值,直至等于0或更小。
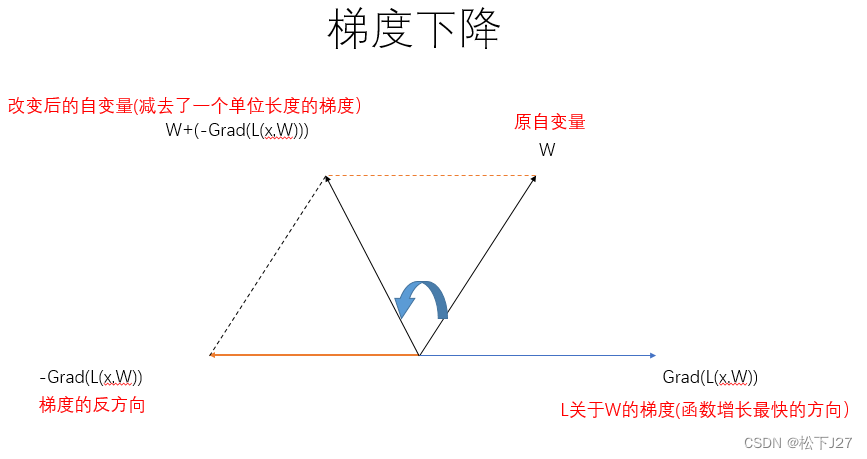
换句话说,**梯度下降法就是要找到能够令损失函数L的值最小值的W。**只不过在找到这一W的过程是循序渐进的(通过调整学习率),并非一蹴而就。
下面是我用python写的一个二元函数的梯度下降法的例子,为了凸显函数关于某一个维度的变化,即,为了模拟损失函数L(W,x)只关于W去更新,使得损失函数L最小化。我的这个例子是让二元函数f(x,y)只关于x更新的demo。
python
import numpy as np
import matplotlib.pyplot as plt
#目标函数
def f(x,y):
return (x-1)**2+(y-3)**2
#目标函数关于x的梯度
def f_prime(x):
pfpx=2*(x-1)
return pfpx
#SGD只针对 x 变量进行梯度下降
def SGD(x0,y0,lr,it):
points = [[x0,y0]]#x catch
x=x0
for _ in range(it):
grad=f_prime(x)
x-=lr*grad
points.append([x,y0])
return np.array(points)
#main
x0=5
y0=5
lr=0.1
it=20
points=SGD(x0,y0,lr,it)
# 绘制目标函数
x = np.linspace(-3, 7, 400)
y = np.linspace(0, 7, 400)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
#绘制等高线图
plt.figure(figsize=(10, 6))
plt.contour(X, Y, Z, levels=np.logspace(-1, 3, 20), cmap='jet')
# 绘制梯度下降的点
plt.plot(points[:, 0], points[:, 1], 'ro-')
# 显示起点和终点
plt.plot(x0, y0, 'go', label='Starting point')
plt.plot(points[-1, 0], points[-1, 1], 'bo', label='End point')
#显示令原函数为0的点
plt.plot(1,3,'k^',label='f(x,y)=0')
# 图形设置
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent Optimization for $f(x, y) = (x - 1)^2 + (y - 3)^2$ (Only updating x)')
plt.legend()
plt.grid(True)
plt.show()
# 绘制三维图像
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
surface = ax.plot_surface(X, Y, Z, cmap='RdYlBu', alpha=0.5, edgecolor='none')
# 设置视角
ax.view_init(elev=30, azim=100) # 例如,仰角为30度,方位角为45度
# 绘制梯度下降的点
points_z = f(points[:, 0], points[:, 1])
ax.plot(points[:, 0], points[:, 1], points_z, 'ro-', markersize=5, label='Gradient Descent Path')
# 显示起点和终点
ax.scatter(x0, y0, f(x0, y0), color='g', s=100, label='Starting Point')
ax.scatter(points[-1, 0], points[-1, 1], points_z[-1], color='b', s=100, label='End Point')
#显示令原函数为0的点
ax.scatter(1,3,f(1,3),color='k',marker='^',s=100,label='f(x,y)=0')
# 添加颜色条
fig.colorbar(surface, shrink=0.5, aspect=10)
# 图形设置
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Gradient Descent on $f(x, y) = (x - 1)^2 + (y - 3)^2$ (Only updating x)')
ax.legend()
plt.show()
运行结果:
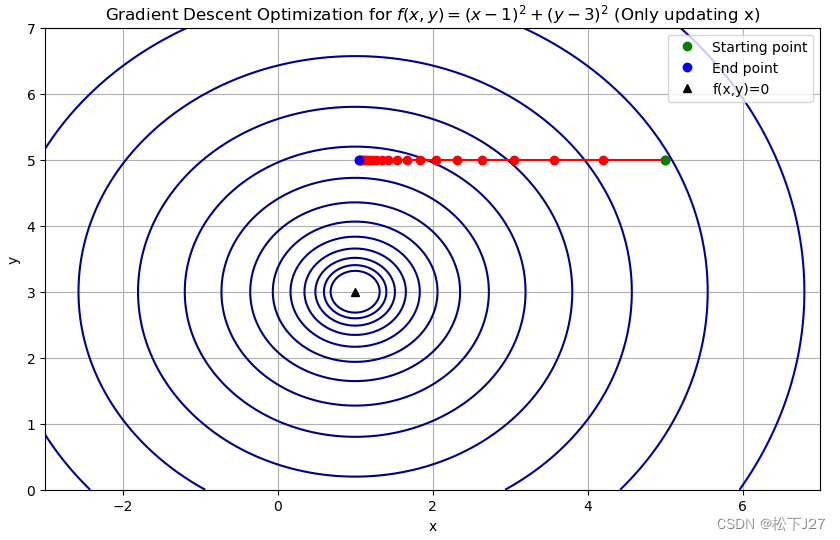
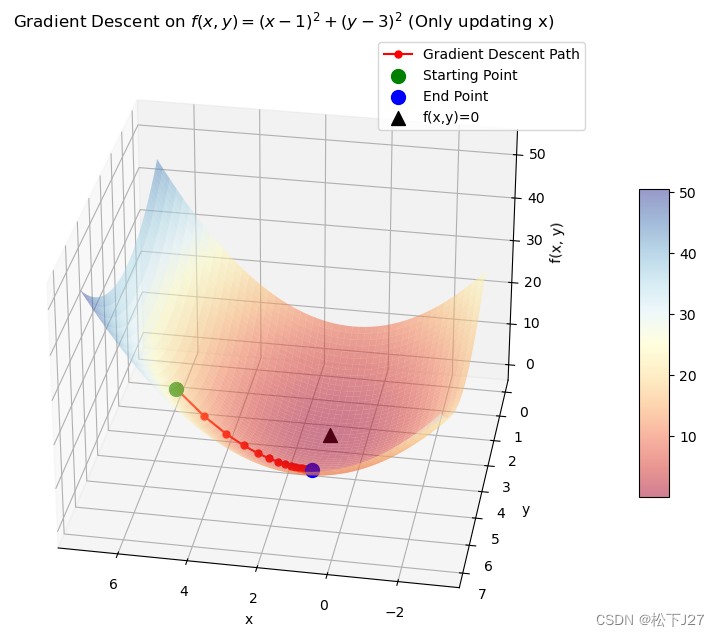
从运行结果中可以看到,因为整个迭代过程只用到了f(x,y)关于x的偏导(限制了y的更新),因此,本来应该沿着令f(x,y)为0的点[x=1,y=3](此时函数值最小等于0)移动的start point,现在只有x方向的移动,即朝着x=1移动。
如果能同时更新两个自变量,则自变量会朝着目标点,即朝着函数值为0的黑三角移动。
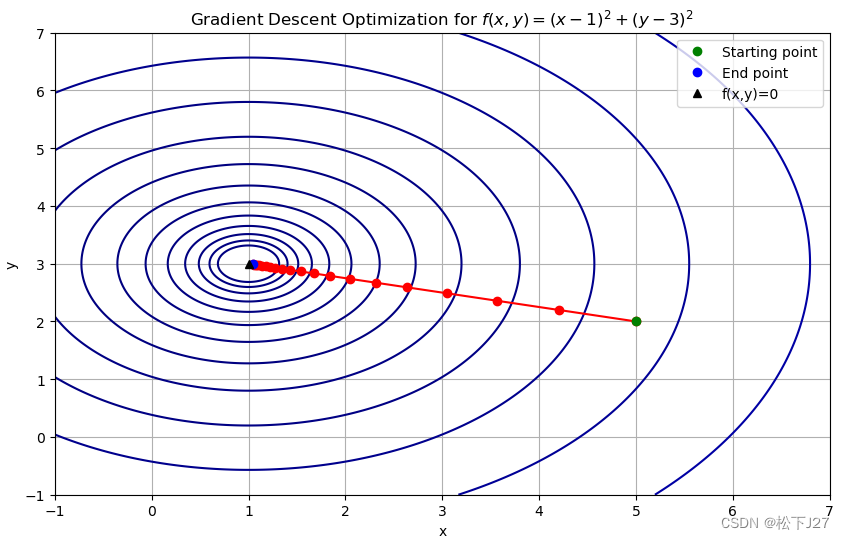

相应的python代码为:
python
import numpy as np
import matplotlib.pyplot as plt
#目标函数
def f(x,y):
return (x-1)**2+(y-3)**2
#目标函数关于全部自变量的梯度
def f_prime(x,y):
pfpx=2*(x-1)
pfpy=2*(y-3)
grad=np.array([pfpx,pfpy])
return grad
#SGD
def SGD(x0,y0,lr,it):
points = [[x0,y0]]#x catch
x=x0
y=y0
for _ in range(it):
grad=f_prime(x,y)
x-=lr*grad[0]
y-=lr*grad[1]
points.append([x,y])
return np.array(points)
#main
x0=5
y0=2
lr=0.1
it=20
points=SGD(x0,y0,lr,it)
# 绘制目标函数
x = np.linspace(-1, 7, 400)
y = np.linspace(-1, 7, 400)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
#绘制等高线图
plt.figure(figsize=(10, 6))
plt.contour(X, Y, Z, levels=np.logspace(-1, 3, 20), cmap='jet')
# 绘制梯度下降的点
plt.plot(points[:, 0], points[:, 1], 'ro-')
# 显示起点和终点
plt.plot(x0, y0, 'go', label='Starting point')
plt.plot(points[-1, 0], points[-1, 1], 'bo', label='End point')
#显示令原函数为0的点
plt.plot(1,3,'k^',label='f(x,y)=0')
# 图形设置
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent Optimization for $f(x, y) = (x - 1)^2 + (y - 3)^2$ ')
plt.legend()
plt.grid(True)
plt.show()
# 绘制三维图像
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
surface = ax.plot_surface(X, Y, Z, cmap='RdYlBu', alpha=0.5, edgecolor='none')
# 设置视角
ax.view_init(elev=30, azim=60) # 例如,仰角为30度,方位角为45度
# 绘制梯度下降的点
points_z = f(points[:, 0], points[:, 1])
ax.plot(points[:, 0], points[:, 1], points_z, 'ro-', markersize=5, label='Gradient Descent Path')
# 显示起点和终点
ax.scatter(x0, y0, f(x0, y0), color='g', s=100, label='Starting Point')
ax.scatter(points[-1, 0], points[-1, 1], points_z[-1], color='b', s=100, label='End Point')
#显示令原函数为0的点
ax.scatter(1,3,f(1,3),color='k',marker='^',s=100,label='f(x,y)=0')
# 添加颜色条
fig.colorbar(surface, shrink=0.5, aspect=5)
# 图形设置
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Gradient Descent on $f(x, y) = (x - 1)^2 + (y - 3)^2$ ')
ax.legend()
plt.show()5,3 常规梯度下降法的不足之处

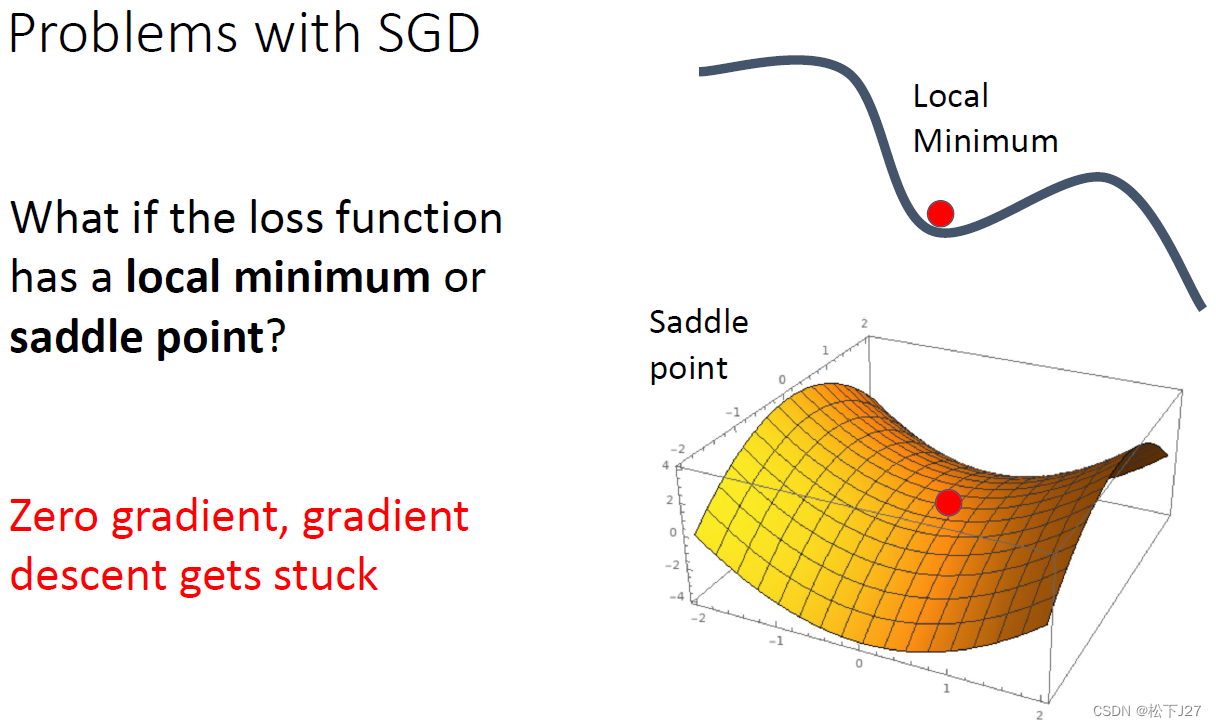
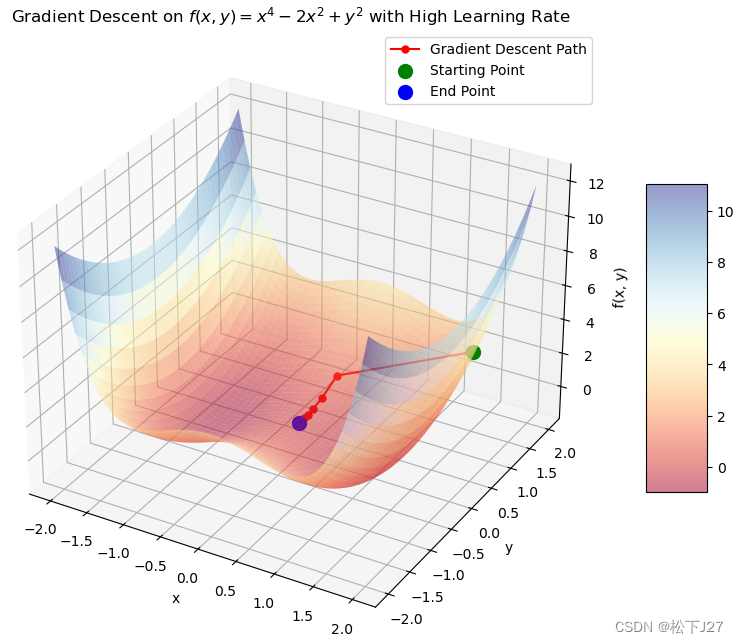
由于梯度下降法本身就是在不断地沿着梯度的反方向下降,直到找到最低点。因此,当该点下降到局部最低点时,或者是下降到一个平坦区域时,就无法继续下降了。而此时所对应的函数值并不是函数的最小值。
例如下面这种情况:
python
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 目标函数
def f(x, y):
return x**4 - 2 * x**2 + y**2
# 目标函数关于全部自变量的梯度
def f_prime(x, y):
df_dx = 4 * x**3 - 4 * x
df_dy = 2 * y
return np.array([df_dx, df_dy])
# SGD
def SGD(x0, y0, lr, it):
points = [[x0, y0]]
x, y = x0, y0
for _ in range(it):
grad = f_prime(x, y)
x -= lr * grad[0]
y -= lr * grad[1]
points.append([x, y])
return np.array(points)
# 参数设置
x0 = 0
y0 = 1.5
lr = 0.5 # 较大的学习率
it = 30
# 执行梯度下降法
points = SGD(x0, y0, lr, it)
# 绘制等高线图
plt.figure(figsize=(10, 6))
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
contour=plt.contour(X, Y, Z, levels=np.linspace(-2, 2, 100), cmap='jet')
plt.colorbar(contour, shrink=0.8, extend='both') # 添加颜色条
# 绘制梯度下降的点
plt.plot(points[:, 0], points[:, 1], 'ro-')
# 显示起点和终点
plt.plot(x0, y0, 'go', label='Starting point')
plt.plot(points[-1, 0], points[-1, 1], 'bo', label='End point')
# 图形设置
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent Optimization for $f(x, y) = x^4 - 2x^2 + y^2$ with High Learning Rate')
plt.legend()
plt.grid(True)
plt.show()
# 绘制三维图像
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
surface = ax.plot_surface(X, Y, Z, cmap='RdYlBu', alpha=0.5)
# 绘制梯度下降的点
points_z = f(points[:, 0], points[:, 1])
ax.plot(points[:, 0], points[:, 1], points_z, 'ro-', markersize=5, label='Gradient Descent Path')
# 显示起点和终点
ax.scatter(x0, y0, f(x0, y0), color='g', s=100, label='Starting Point')
ax.scatter(points[-1, 0], points[-1, 1], points_z[-1], color='b', s=100, label='End Point')
# 添加颜色条
fig.colorbar(surface, shrink=0.5, aspect=5)
# 图形设置
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Gradient Descent on $f(x, y) = x^4 - 2x^2 + y^2$ with High Learning Rate')
ax.legend()
plt.show()这是起始点的选择不恰当引起的的:
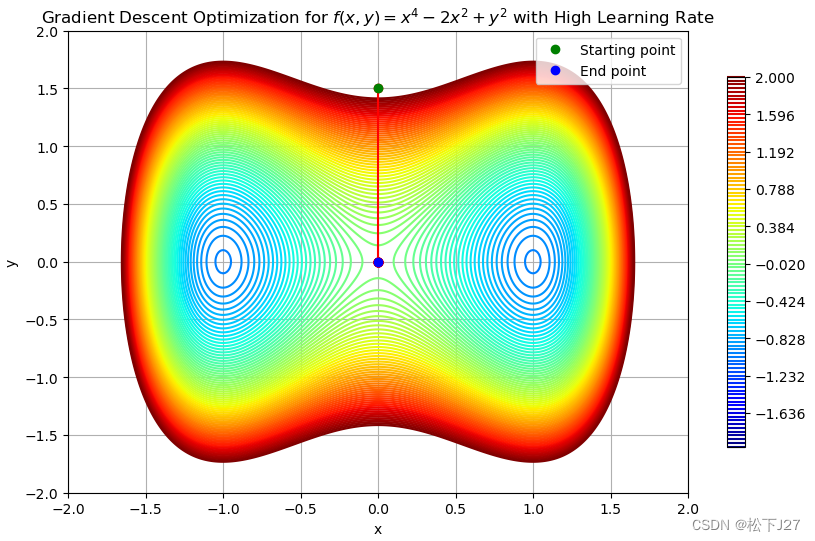
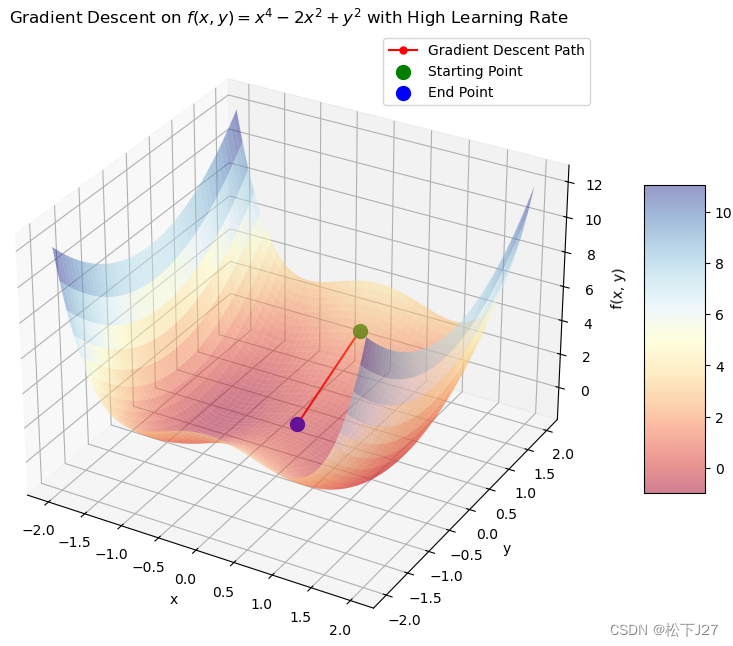
这是学习率的选择引起的:

5,4 SGD+momentum
为了克服传统梯度下降法的缺点,即,碰到local min或saddle points时失效的情况。

SGD+Momentum相对于之前的变化在于,原有的SGD是走一步算一步梯度,然后再按这个梯度更新,因此如果走到了局部最小值处或者鞍点,当前点的梯度就为0。梯度为0,就走不下去了,只能在原点大转。
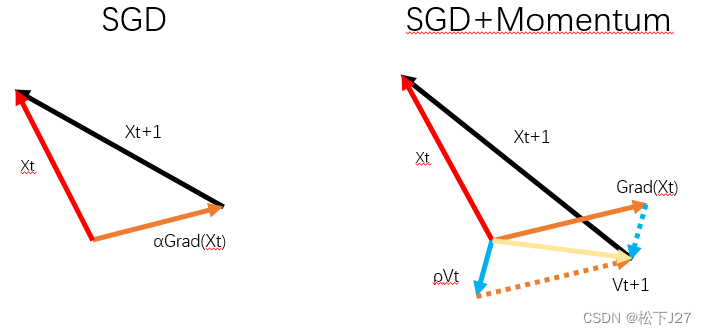
SGD+Momentum为了让点继续走下去,就引入了"惯性"的概念。具体来说,Momentum在更新时不光考虑当前点的梯度,也会考虑前一步的梯度。也就是在走这一步之前,把上一步的惯性也考虑进去。
比如说前面遇到的鞍点或局部最低点,因为按照前一点的梯度去更新,正好走到了这里。但如果前一点所使用的梯度是加上了上上一点的梯度的,也就是加上了惯性,那么这一步就比SGD迈的大,迈的远。
就好像下图中的黑圈,如果按照SGD的梯度走,则正好走到红点的位置。但如果加上了上一步的惯性,步子迈的要比SGD大,就能成功的越过局部低点和鞍点继续往下走。

对于SGD+Momentum而言,下面两个公式 是等价的:

5,5 Nesterov Momentum
SGD+Momentum的出现是为了能够越过局部最低点和鞍点,但有时候如果步子迈的太大也不好,即,冲过头了。例如,在已经快接近全局最低点的地方,需要反复几次才能走到最低点,也就是会出现震荡。
Nesterov Momentum的做法是,不再按照当前点的梯度+前一点的梯度 去走。而是按照下一步的梯度+前一点的梯度去跟新。
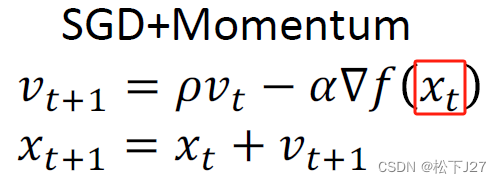
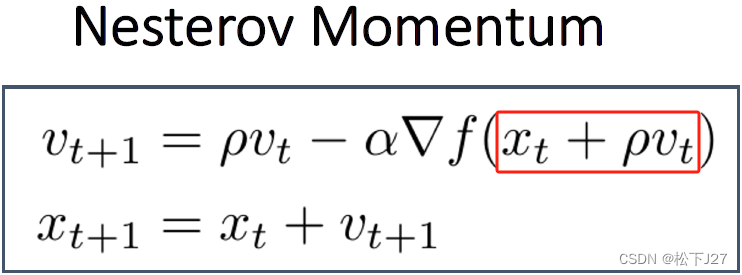
这样就能防止步子迈的过大,使初始点在下降的过程中,既能越过鞍点和局部最低点,也能避免震荡。
小结:
不论是SGD+Momentum还是Nesterov Momentum算法都是借助物理中动量的概念设计的算法。下面会介绍一些别的算法如Adagrad, RMSprop和Adam等,他们都属于自适应算法,通过自适应的调整学习率,处理不同梯度的变化,帮助越过鞍点。
5,6 AdaGrad(Adaptive Gradient Algorithm)
AdaGrad(Adaptive Gradient Algorithm)是一种自适应学习率优化算法,它根据历史的梯度来调整每次的学习率。

他的整体思路跟SGD一样,还是用原始梯度乘以学习率去更新W。所不同的是,他用梯度的平方和的平方根作为对学习率的惩罚(惩罚就是让学习率除以这个值)去动态的调整学习率。走的步数越多,梯度的平方和就越大,惩罚的就越厉害。
因此,刚开始的时候学习率的衰减小,即步伐大。越是到了后面,学习率的衰减就越来越大,下降的步伐也就会越来越小。这也符合梯度下降的构想,刚开始的时候步伐大,容易越过鞍点和局部小值点,到了后面越是接近全局最小值点了,步子也正好应该小了,免得出现震荡。
5,7 RMSProp
AdaGrad的效果很好,但有一个潜在的问题,也就是他的那个自适应的惩罚项。随着步数增多,对学习率的惩罚越来越大,这也是我们希望看到了,因为,大概了这个时候已经下降到函数的最低点了。但如果没有呢?
也就是说,如果还没有走到谷底,对学习率的惩罚就已经很大了呢?这个时候,就好像梯度消失一样,学习率几乎为0,w无法更新了。相当于是眼看着就要到谷底了,却脚崴了,走不动道了。因此,RMSProp就对AdaGrad的这一问题进行了改进。
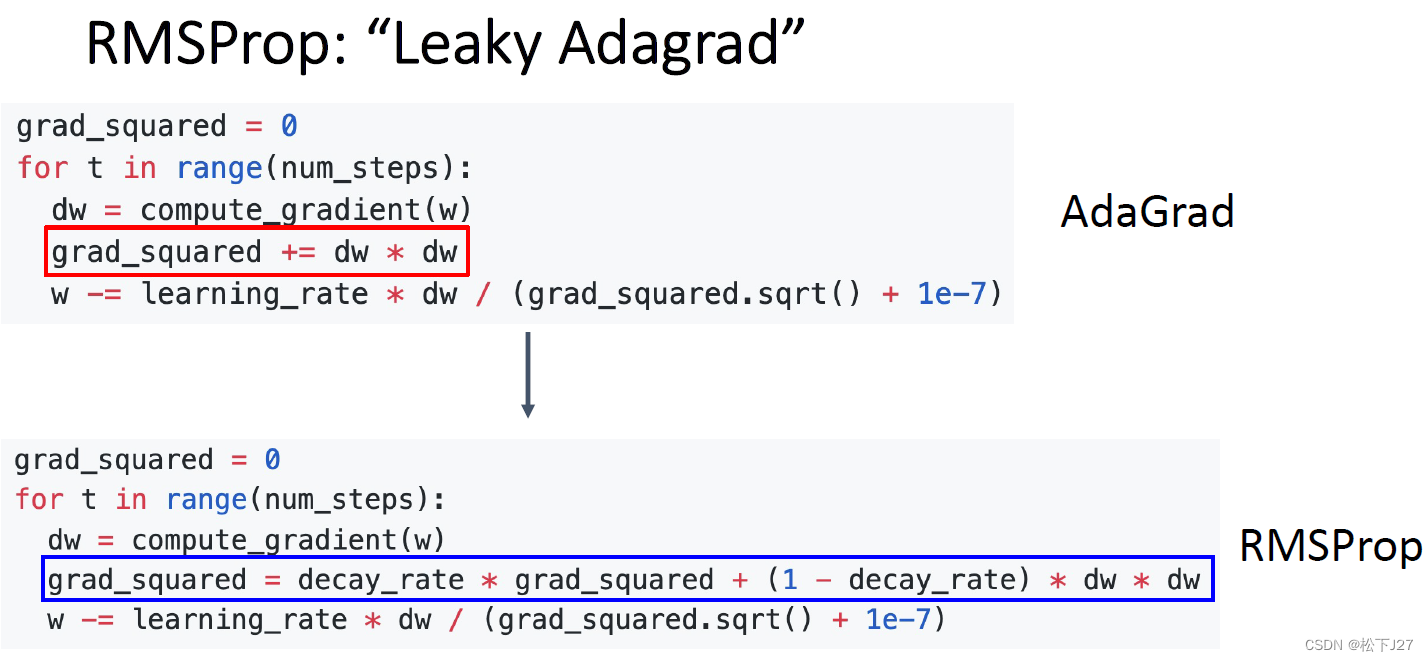
在grad_sqared的计算中RMSProp加入了一个系数decay_rate。根据公式可以看出,当decay_rate为0时,RMSProp就退化成了AdaGrad算法,此时学习率的惩罚项依然是梯度的平方和开根号。当decay_rate为1时,每一步学习率的惩罚项都等于当前梯度的平方根,即只与当前梯度有关。
这也就是说,随着decay_rate这个参数从0逐渐增加到1,对学习率的惩罚也越来越弱。这样就能避免步数太多了以后崴脚的情况。
(全文完)
--- 作者,松下J27
参考文献(鸣谢):
1,Stanford University CS231n: Deep Learning for Computer Vision
3,10 Training Neural Networks I_哔哩哔哩_bilibili
4,Schedule | EECS 498-007 / 598-005: Deep Learning for Computer Vision
**版权声明:**所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27