【数据结构 - 二叉树】

1. 什么是二叉树？

在计算机科学中，二叉树是一种重要的数据结构，它由节点（node）组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的设计灵活性使其在各种应用中都有广泛的用途。

2. 基本概念

二叉树有几个关键的概念需要理解：

根节点（Root）：树的顶端节点，没有父节点。
子节点（Child）：某节点下面的节点。
父节点（Parent）：某节点上面的节点。
叶子节点（Leaf）：没有子节点的节点。
深度（Depth）：从根节点到某节点的唯一路径的长度。
高度（Height） ：从某节点到一个叶节点最长路径的长度。

3. 树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

cpp 复制代码

typedef int DataType;
struct Node
{
 struct Node* firstChild1; // 第一个孩子结点
 struct Node* pNextBrother; // 指向其下一个兄弟结点
 DataType data; // 结点中的数据域
};

4. 二叉树的分类

二叉树有多种类型，每种类型都有其独特的特点和应用场景：

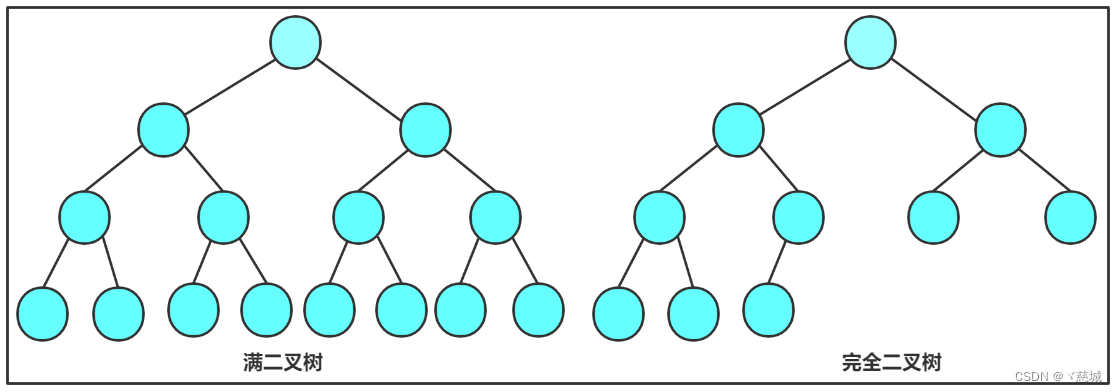
满二叉树：所有叶子节点都在同一层，每个非叶子节点都有两个子节点。
完全二叉树：除了最后一层，其它层的节点都是满的，最后一层的节点集中在左边。
平衡二叉树（AVL树）：任意节点的左右子树高度差不超过1，保证了查找、插入和删除的平均时间复杂度为O(log n)。
二叉搜索树（BST）：左子树上所有节点的值均小于它的根节点的值，右子树上所有节点的值均大于它的根节点的值，支持高效的查找、插入和删除操作。

5. 二叉树的基本操作

二叉树的基本操作包括：

插入节点：根据规则将新节点插入到合适的位置。
删除节点：删除指定节点，并根据需要调整树的结构。
查找节点：根据指定的值查找节点。

遍历：按照特定顺序访问树的所有节点，包括层次遍历、前序、中序和后序遍历。

         1
       /   \
      2     3
     / \   / \
    4   5 6   7

前序遍历（先根遍历）
- 访问顺序：根节点 -> 左子树 -> 右子树。
- 前序遍历的结果为：1 2 4 5 3 6 7
中序遍历（中根遍历）
- 访问顺序：左子树 -> 根节点 -> 右子树。
- 中序遍历的结果为：4 2 5 1 6 3 7
后序遍历（后根遍历）
- 访问顺序：左子树 -> 右子树 -> 根节点。
- 该二叉树的后序遍历结果为：4 5 2 6 7 3 1

代码实现：

下面是一个简单的C语言示例，展示如何实现二叉树的前序、中序和后序遍历。我们首先定义二叉树的节点结构 TreeNode 和一些基本操作函数，然后分别实现每种遍历方式的函数。

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>

// 二叉树节点结构定义
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 创建新节点
struct TreeNode* newNode(int data) {
    struct TreeNode* node = (struct TreeNode*) malloc(sizeof(struct TreeNode));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 前序遍历函数
void preorder(struct TreeNode* root) {
    if (root != NULL) {
        printf("%d ", root->data); // 访问根节点
        preorder(root->left);      // 前序遍历左子树
        preorder(root->right);     // 前序遍历右子树
    }
}

// 中序遍历函数
void inorder(struct TreeNode* root) {
    if (root != NULL) {
        inorder(root->left);       // 中序遍历左子树
        printf("%d ", root->data); // 访问根节点
        inorder(root->right);      // 中序遍历右子树
    }
}

// 后序遍历函数
void postorder(struct TreeNode* root) {
    if (root != NULL) {
        postorder(root->left);     // 后序遍历左子树
        postorder(root->right);    // 后序遍历右子树
        printf("%d ", root->data); // 访问根节点
    }
}

// 主函数
int main() {
    // 创建一个示例二叉树
    struct TreeNode* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    printf("前序遍历结果：");
    preorder(root);
    printf("\n");

    printf("中序遍历结果：");
    inorder(root);
    printf("\n");

    printf("后序遍历结果：");
    postorder(root);
    printf("\n");

    return 0;
}

结果输出

运行以上代码，将输出如下结果：

前序遍历结果：1 2 4 5 3

中序遍历结果：4 2 5 1 3

后序遍历结果：4 5 2 3 1

层次遍历

层次遍历需要借助队列来实现，以确保每一层的节点按顺序被访问。

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 辅助队列节点结构
struct QueueNode {
    struct TreeNode* treeNode;
    struct QueueNode* next;
};

// 定义队列结构
struct Queue {
    struct QueueNode *front, *rear;
};

// 创建新的二叉树节点
struct TreeNode* newNode(int data) {
    struct TreeNode* node = (struct TreeNode*) malloc(sizeof(struct TreeNode));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 创建空队列
struct Queue* createQueue() {
    struct Queue* queue = (struct Queue*) malloc(sizeof(struct Queue));
    queue->front = queue->rear = NULL;
    return queue;
}

// 入队操作
void enqueue(struct Queue* queue, struct TreeNode* treeNode) {
    struct QueueNode* newNode = (struct QueueNode*) malloc(sizeof(struct QueueNode));
    newNode->treeNode = treeNode;
    newNode->next = NULL;
    if (queue->rear == NULL) {
        queue->front = queue->rear = newNode;
        return;
    }
    queue->rear->next = newNode;
    queue->rear = newNode;
}

// 出队操作
struct TreeNode* dequeue(struct Queue* queue) {
    if (queue->front == NULL)
        return NULL;
    struct TreeNode* treeNode = queue->front->treeNode;
    struct QueueNode* temp = queue->front;
    queue->front = queue->front->next;
    if (queue->front == NULL)
        queue->rear = NULL;
    free(temp);
    return treeNode;
}

// 层次遍历函数
void levelOrder(struct TreeNode* root) {
    if (root == NULL) return;
    struct Queue* queue = createQueue();
    enqueue(queue, root);

    while (queue->front != NULL) {
        struct TreeNode* currentNode = dequeue(queue);
        printf("%d ", currentNode->data);

        if (currentNode->left != NULL)
            enqueue(queue, currentNode->left);
        if (currentNode->right != NULL)
            enqueue(queue, currentNode->right);
    }
}

// 主函数
int main() {
    // 创建一个示例二叉树
    struct TreeNode* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    printf("层次遍历结果：");
    levelOrder(root);
    printf("\n");

    return 0;
}

层次遍历结果：1 2 3 4 5

6. 二叉树的性质

cpp 复制代码

     5
   /   \
  3     7
 / \   / \
1   4 6   8

1. 在二叉树的第 i 层上至多有 2^(i - 1) 个节点（i >= 1）。

例如，在上述二叉树的第 3 层，最多有 2^(3 - 1) = 4 个节点。

2. 深度为 k 的二叉树至多有 2^k - 1 个节点（k >= 1）****。

对于这个示例二叉树，深度为 3，节点总数最多为 2^3 - 1 = 7 个。

3. 对任何一棵二叉树，如果其终端节点数为 n0，度为 2 的节点数为 n2，则 n0 = n2 + 1。

7. 实际应用

二叉树在现实世界中有多种应用，例如：

文件系统的目录结构可以使用二叉树来组织。
数据库系统中索引的实现通常采用二叉树或其衍生结构。
编译器中的语法分析阶段可以利用二叉树来表示语法树。

结语

通过本文，我们全面介绍了二叉树的基本概念、分类、基本操作和实际应用。二叉树作为一种核心数据结构，不仅在理论计算机科学中占有重要地位，而且在实际应用中有广泛的运用。深入理解二叉树将有助于提升编程能力和解决实际问题的能力。