复制代码
import numpy as np
#from numpy.fft import fft, fftfreq
from scipy.fftpack import fft, rfft, irfft, fftfreq, rfftfreq
import scipy.signal
import matplotlib.pyplot as plt
%matplotlib inline
Basic signal and plot
复制代码
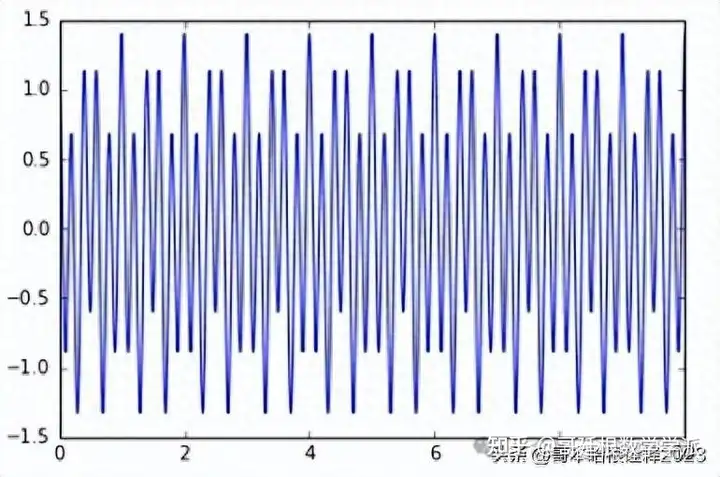
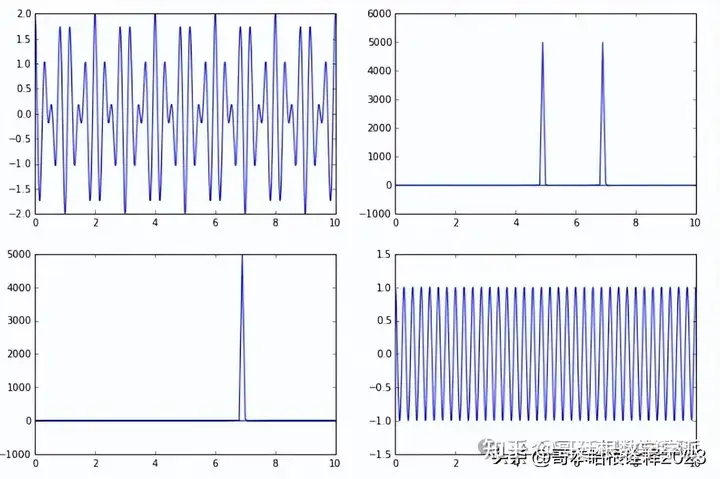
dt = 0.001
T = 10
f = 2
f1 = 5
t = np.linspace(0, T, T/dt)
signal = 0.4 * np.cos(2*np.pi*f*t) + np.cos(2*np.pi*f1*t)
plt.plot(t, signal)
plt.show()
复制代码
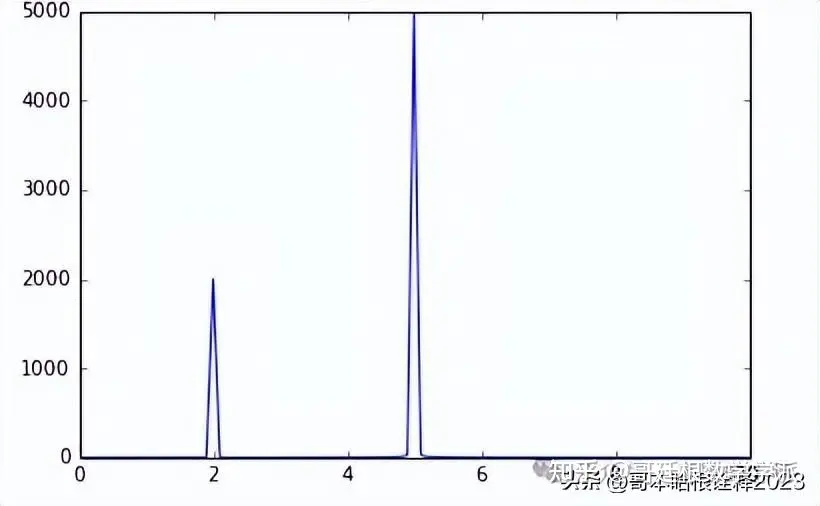
SIGNAL = fft(signal)
freq = fftfreq(signal.size, d=dt)
freq
# Chop off the negative frequencies
keep = freq>=0
SIGNAL = SIGNAL[keep]
freq = freq[keep]
ax1 = plt.subplot(111)
ax1.plot(freq, np.abs(SIGNAL))
ax1.set_xlim(0,10)
plt.show()
复制代码
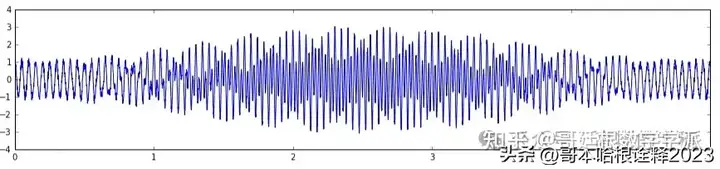
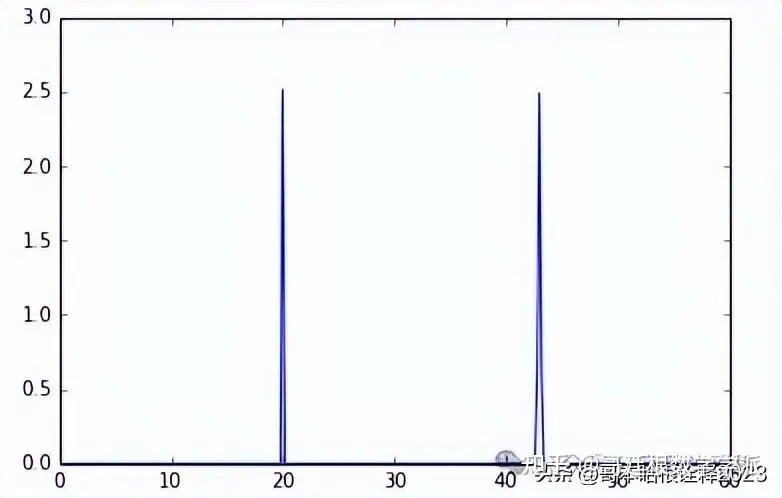
dt = 0.001
t = np.arange(0.0, 5.0, dt)
s1 = np.cos(2*np.pi*20*t)
s2 = 2*np.cos(2*np.pi*43*t)
# create a transient
#mask = np.where(np.logical_and(t>1, t<4), 1.0, 0.0)
w = scipy.signal.hann(5000)
s2 = s2 * w
# add some noise into the mix
nse = 0.1*np.random.randn(len(t))
x = s1 + s2 + nse # the signal
NFFT = 256 # the length of the windowing segments
Fs = int(1.0/dt) # the sampling frequency
plt.figure(figsize=(15,3))
plt.subplot(111)
plt.plot(t, x)
plt.show()
复制代码
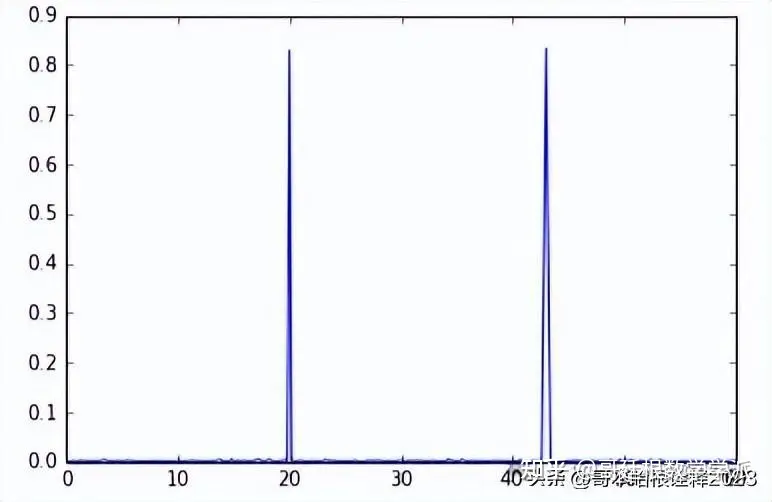
X = fft(x)
freq = fftfreq(x.size, d=dt)
keep = freq>=0 # only positive frequencies
X = X[keep]
freq = freq[keep]
ax1 = plt.subplot(111)
ax1.plot(freq, np.absolute(X)/3000.)
ax1.set_xlim(0,60)
plt.show()
Compare to PSDs
复制代码
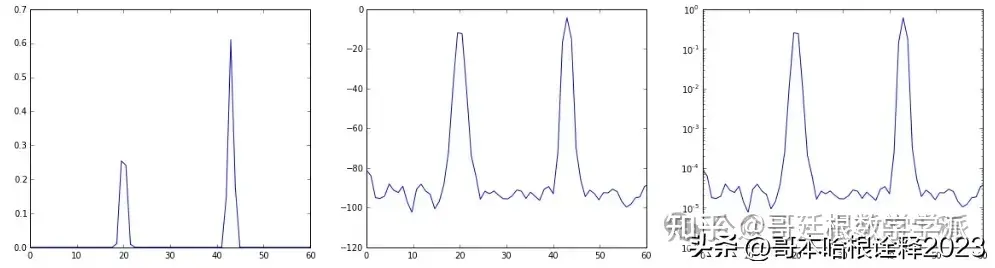
import scipy.signal
f, P = scipy.signal.periodogram(x, Fs)
ax1 = plt.subplot(111)
ax1.plot(f, P)
ax1.set_xlim(0,60)
plt.show()
Welch's method
复制代码
f, P = scipy.signal.welch(x, Fs, nperseg=1024)
plt.figure(figsize=(20,5))
ax1 = plt.subplot(131)
ax1.plot(f, P)
ax1.set_xlim(0,60)
ax2 = plt.subplot(132)
ax2.plot(f, 20*np.log10(P))
ax2.set_xlim(0,60)
ax3 = plt.subplot(133)
ax3.semilogy(f, P) # Note plot type... same as taking 20*np.log10(P)
ax3.set_xlim(0,60)
plt.show()
复制代码
def onedplot(dt=0.001, T=1.0, view=None, support=0.128, noise=0.0, f=60.0, window=None, perturb=None, title=None, ylim=None):
if not view:
view = T
# The lead time outside the support
lead = (T - support)/2.0
# The time basis
t = np.linspace(0.0, T, T/dt)
s1 = np.sin(2*np.pi*f*t)
# create a transient
mask = np.where(np.logical_and(t>lead, t<(lead+support)), 1.0, 0.0)
x = s1 * mask
windows = {'hann': scipy.signal.hann, 'boxcar': scipy.signal.boxcar}
if window:
w = windows[window[0]](window[1])
if window[1] < x.size:
l = int((x.size-window[1])/2.0)
x[:l] = 0.0
x[l:-l] *= w
x[-l:] = 0.0
else:
x *= w
# add some noise into the mix
nse = noise * np.random.randn(len(t))
x += nse
SIGNAL = abs(fft(x))
freq = fftfreq(x.size, d=dt)
keep = freq>=0 # only positive frequencies
SIGNAL = SIGNAL[keep]
freq = freq[keep]
plt.figure(figsize=(18,3))
ax1 = plt.subplot(121)
ax1.plot(t, x)
ax1.set_ylim(-1.2, 1.2)
ax1.set_xlim(0, view)
if title:
plt.title(title)
else:
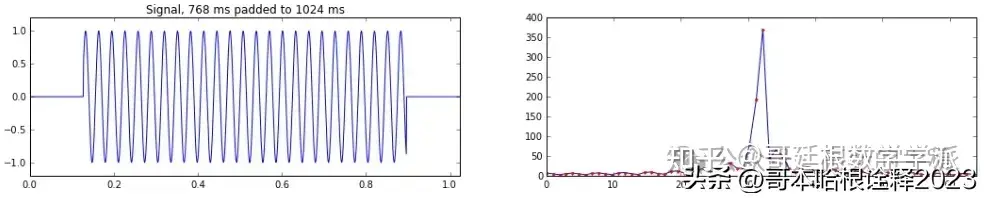
plt.title('Signal, {0:.0f} ms padded to {1:.0f} ms'.format(support*1000, T*1000))
ax2 = plt.subplot(122)
ax2.set_xlim(0, 2*f)
if ylim:
ax2.set_ylim(0, ylim)
if perturb:
s2 = np.sin(2*np.pi*(f+perturb)*t)
s3 = np.sin(2*np.pi*(f-perturb)*t)
x2 = s2 * mask + nse
x3 = s3 * mask + nse
if window:
x2 *= w
x3 *= w
SIGNAL2 = abs(fft(x2))
SIGNAL3 = abs(fft(x3))
SIGNAL2 = SIGNAL2[keep]
SIGNAL3 = SIGNAL3[keep]
ax1.plot(t, x2)
ax1.plot(t, x3)
ax2.plot(freq, SIGNAL)
ax2.plot(freq, SIGNAL, '.', color='blue')
print(freq.size, SIGNAL.size, SIGNAL2.size)
ax2.plot(freq, SIGNAL2)
ax2.plot(freq, SIGNAL2, '.', color='green')
ax2.plot(freq, SIGNAL3)
ax2.plot(freq, SIGNAL3, '.', color='red')
else:
ax2.plot(freq, SIGNAL)
ax2.plot(freq, SIGNAL, '.', color='red')
plt.show()
dt = 0.001
T = 0.256
view = 1.024
support = 0.128
noise = 0.0
f = 32
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f)
复制代码
T = 1.024
support = 0.128
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f)
复制代码
T = 1.024
support = 0.768
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f)
复制代码
from IPython.html import widgets
def slidy_signal(**kwargs):
dt = 0.001
f = 2
onedplot(dt=dt, f=f, **kwargs)
widgets.interactive(slidy_signal, T=4, support=2.5, noise=0.0)
复制代码
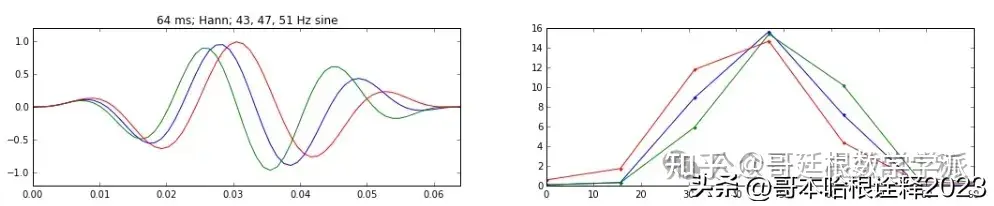
T = 0.064
support = 0.064
view = 0.064
f = 45.0
title = '64 ms; Hann; 43, 47, 51 Hz sine'
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('hann', 64), perturb=4.0, title=title)
复制代码
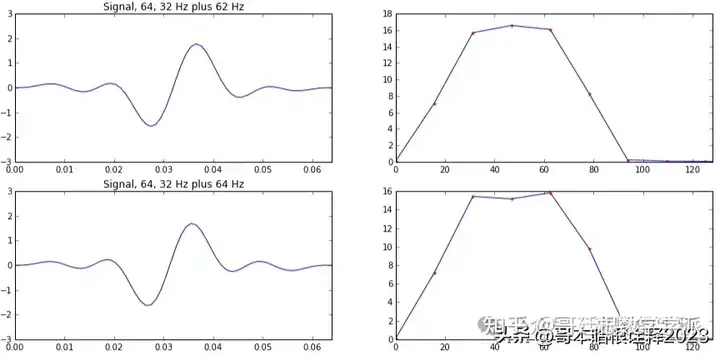
dt = 0.001
T = 0.064
view = 0.064
support = 0.064
noise = 0.0
f = 32
f1 = 62
f2 = 64
lead = (T - support)/2.0
t = np.linspace(0.0, T, T/dt)
s1 = np.sin(2*np.pi*f*t) + np.sin(2*np.pi*f1*t)
s2 = np.sin(2*np.pi*f*t) + np.sin(2*np.pi*f2*t)
mask = np.where(np.logical_and(t>lead, t<(lead+support)), 1.0, 0.0)
nse = noise * np.random.randn(len(t))
window = scipy.signal.hann(s1.size)
signal1 = s1 * mask * window + nse
signal2 = s2 * mask * window + nse
SIGNAL1 = abs(fft(signal1))
SIGNAL2 = abs(fft(signal2))
freq = fftfreq(signal1.size, d=dt)
keep = freq>=0 # only positive frequencies
SIGNAL1 = SIGNAL1[keep]
SIGNAL2 = SIGNAL2[keep]
freq = freq[keep]
plt.figure(figsize=(15,7))
ax1 = plt.subplot(221)
ax1.plot(t, signal1)
ax1.set_ylim(-3, 3)
ax1.set_xlim(0, view)
plt.title('Signal, {0:.0f}, {1:.0f} Hz plus {2:.0f} Hz'.format(support*1000, f, f1))
ax2 = plt.subplot(222)
ax2.set_xlim(0, 2*f2)
ax2.plot(freq, SIGNAL1)
ax2.plot(freq, SIGNAL1, '.', color='red')
ax3 = plt.subplot(223)
ax3.plot(t, signal2)
ax3.set_ylim(-3, 3)
ax3.set_xlim(0, view)
plt.title('Signal, {0:.0f}, {1:.0f} Hz plus {2:.0f} Hz'.format(support*1000, f, f2))
ax4 = plt.subplot(224)
ax4.set_xlim(0, 2*f2)
ax4.plot(freq, SIGNAL2)
ax4.plot(freq, SIGNAL2, '.', color='red')
plt.show()
复制代码
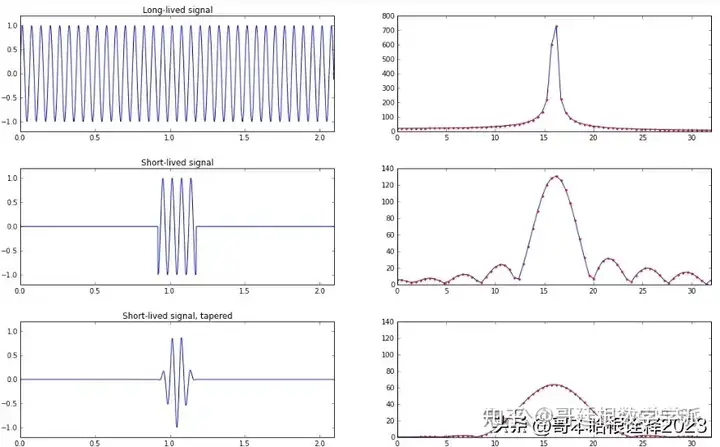
dt = 0.001
T = 2.096
view = 2.096
support = 2.096
noise = 0.0
f = 16
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, title="Long-lived signal")
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('boxcar', 256), title="Short-lived signal")
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('hann', 256), ylim=140, title="Short-lived signal, tapered")
复制代码
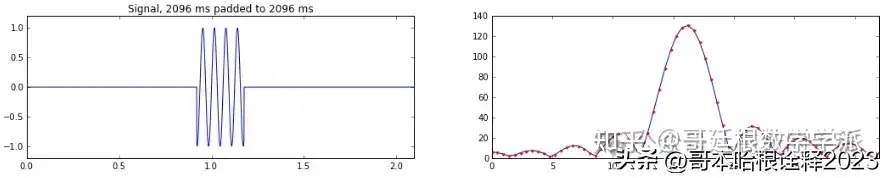
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('boxcar', 256))
复制代码
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('hann', 256), ylim=140)
复制代码
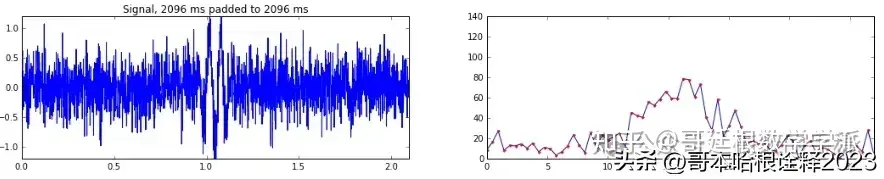
noise = 0.3
onedplot(dt=dt, T=T, view=view, support=support, noise=noise, f=f, window=('hann', 256), ylim=140)
Simple bandpass filter
复制代码
dt = 0.001
T = 10.0
time = np.linspace(0, T, T/dt)
signal = np.cos(5*np.pi*time) + np.cos(7*np.pi*time)
SIGNAL = rfft(signal)
freq = fftfreq(signal.size, d=time[1]-time[0])
# We need -ve frequencies this time...
# keep = freq>=0 # only positive frequencies
# SIGNAL = SIGNAL[keep]
# freq = freq[keep]
# If our original signal time was in seconds, this is now in Hz
cut_SIGNAL = SIGNAL.copy()
cut_SIGNAL[freq<6] = 0
result = irfft(cut_SIGNAL)
plt.figure(figsize=(12,8))
plt.subplot(221)
plt.plot(time, signal)
plt.subplot(222)
plt.plot(freq, SIGNAL)
plt.xlim(0,10)
plt.subplot(223)
plt.plot(freq, cut_SIGNAL)
plt.xlim(0,10)
plt.subplot(224)
plt.plot(time, result)
plt.show()
Effect of sample interval
复制代码
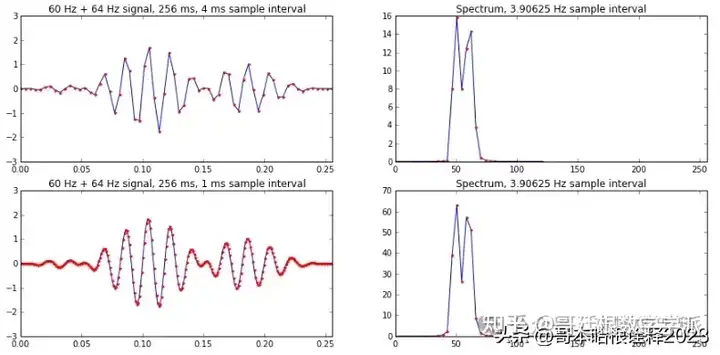
dt1 = 0.004
dt2 = 0.001
T = 0.256
view = 0.256
support = 0.256
noise = 0.0
f = 50
f1 = 60
def sig_gen(dt):
lead = (T - support)/2.0
t = np.linspace(0.0, T, T/dt)
s1 = np.sin(2*np.pi*f*t) + np.sin(2*np.pi*f1*t)
mask = np.where(np.logical_and(t>lead, t<(lead+support)), 1.0, 0.0)
window = scipy.signal.hann(s1.size)
signal = s1 * mask * window
SIGNAL = np.abs(fft(signal))
freq = fftfreq(signal.size, d=dt)
keep = freq>=0 # only positive frequencies
SIGNAL = SIGNAL[keep]
freq = freq[keep]
return t, signal, freq, SIGNAL
t1, signal1, freq1, SIGNAL1 = sig_gen(dt1)
t2, signal2, freq2, SIGNAL2 = sig_gen(dt2)
# PLOTTING
plt.figure(figsize=(15,7))
ax1 = plt.subplot(221)
ax1.plot(t1, signal1)
ax1.plot(t1, signal1, '.', color='red')
ax1.set_ylim(-3, 3)
ax1.set_xlim(0, view)
plt.title('{0} Hz + {1} Hz signal, {2:0.0f} ms, {3:0.0f} ms sample interval'.format(f1, f2, T*1000, dt1*1000))
ax2 = plt.subplot(222)
ax2.set_xlim(0, 4*f2)
ax2.plot(freq1, SIGNAL1)
ax2.plot(freq1, SIGNAL1, '.', color='red')
plt.title('Spectrum, {0} Hz sample interval'.format(1/T))
ax3 = plt.subplot(223)
ax3.plot(t2, signal2)
ax3.plot(t2, signal2, '.', color='red')
ax3.set_ylim(-3, 3)
ax3.set_xlim(0, view)
plt.title('{0} Hz + {1} Hz signal, {2:0.0f} ms, {3:0.0f} ms sample interval'.format(f1, f2, T*1000, dt2*1000))
ax4 = plt.subplot(224)
ax4.set_xlim(0, 4*f2)
ax4.plot(freq2, SIGNAL2)
ax4.plot(freq2, SIGNAL2, '.', color='red')
plt.title('Spectrum, {0} Hz sample interval'.format(1/T))
plt.show()
Effect of precision
复制代码
def quantize(a, values=8):
b = a.reshape(a.size)
b = float(values) * b / np.amax(b)
bins = np.linspace(0, values-1, values)
c = np.digitize(b, bins)
return c.reshape(a.shape)
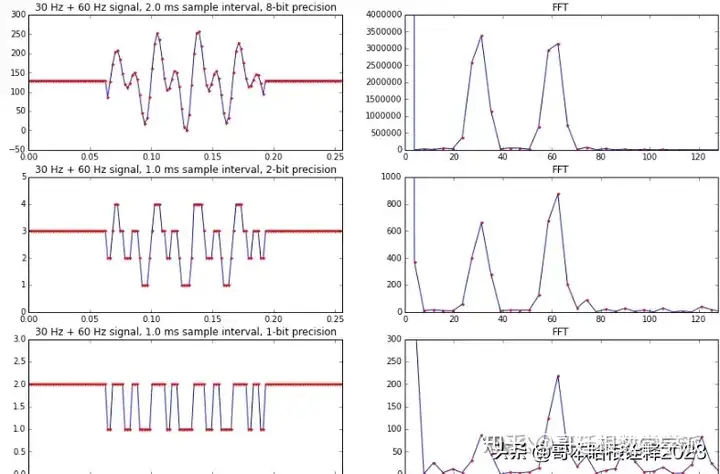
dt = 0.002
T = 0.256
view = 0.256
support = 0.128
noise = 0.0
f = 30
f1 = 60
def sig_quant(q):
lead = (T - support)/2.0
t = np.linspace(0.0, T, T/dt)
s1 = np.sin(2*np.pi*f*t) + np.sin(2*np.pi*f1*t)
mask = np.where(np.logical_and(t>lead, t<(lead+support)), 1.0, 0.0)
window = scipy.signal.hann(s1.size)
signal = s1 * mask * window
signal -= np.amin(signal)
signal = quantize(signal, q)
SIGNAL = np.abs(fft(signal))
freq = fftfreq(signal.size, d=dt)
keep = freq>=0 # only positive frequencies
SIGNAL = SIGNAL[keep]**2.
freq = freq[keep]
return t, signal, freq, SIGNAL
t1, signal1, freq1, SIGNAL1 = sig_quant(256) # 8-bit
t2, signal2, freq2, SIGNAL2 = sig_quant(4) # 2-bit
t3, signal3, freq3, SIGNAL3 = sig_quant(2) # 1-bit
# PLOTTING
plt.figure(figsize=(15,10))
ax1 = plt.subplot(321)
ax1.plot(t1, signal1)
ax1.plot(t1, signal1, '.', color='red')
ax1.set_xlim(0, view)
ax1.set_ylim(-50, 300)
plt.title('{0} Hz + {1} Hz signal, {2} ms sample interval, 8-bit precision'.format(f, f1, dt*1000))
ax2 = plt.subplot(322)
ax2.set_xlim(0, 2*f2)
ax2.plot(freq1, SIGNAL1)
ax2.plot(freq1, SIGNAL1, '.', color='red')
ax2.set_ylim(0, 4e6)
plt.title('FFT')
ax3 = plt.subplot(323)
ax3.plot(t2, signal2)
ax3.plot(t2, signal2, '.', color='red')
ax3.set_xlim(0, view)
ax3.set_ylim(0, 5)
plt.title('{0} Hz + {1} Hz signal, {2} ms sample interval, 2-bit precision'.format(f, f1, dt2*1000))
ax4 = plt.subplot(324)
ax4.set_xlim(0, 2*f2)
ax4.plot(freq2, SIGNAL2)
ax4.plot(freq2, SIGNAL2, '.', color='red')
ax4.set_ylim(0, 1e3)
plt.title('FFT')
ax5 = plt.subplot(325)
ax5.plot(t3, signal3)
ax5.plot(t3, signal3, '.', color='red')
ax5.set_xlim(0, view)
ax5.set_ylim(0, 3)
plt.title('{0} Hz + {1} Hz signal, {2} ms sample interval, 1-bit precision'.format(f, f1, dt2*1000))
ax6 = plt.subplot(326)
ax6.set_xlim(0, 2*f2)
ax6.plot(freq3, SIGNAL3)
ax6.plot(freq3, SIGNAL3, '.', color='red')
ax6.set_ylim(0, 3e2)
plt.title('FFT')
plt.show()
复制代码
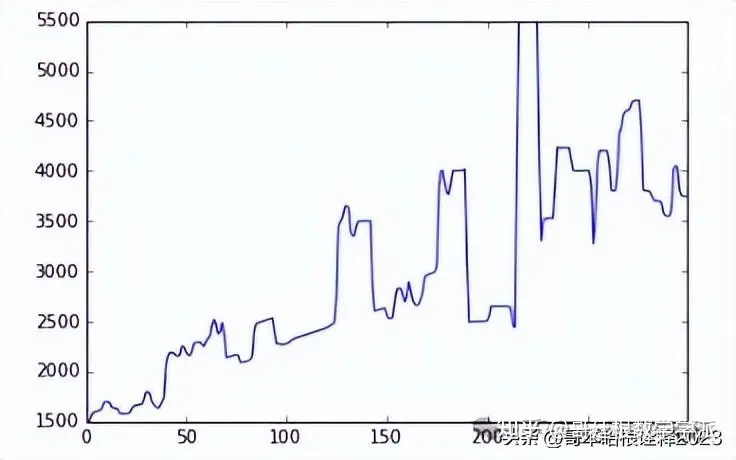
d = np.loadtxt('Marmousi_model_250')
rc = (d[1:] - d[:-1]) / (d[1:] + d[:-1] )
plt.plot(d)
Sampling and aliasing
复制代码
# Import IPython's interact function which is used below to
# build the interactive widgets
from IPython.html.widgets import interact
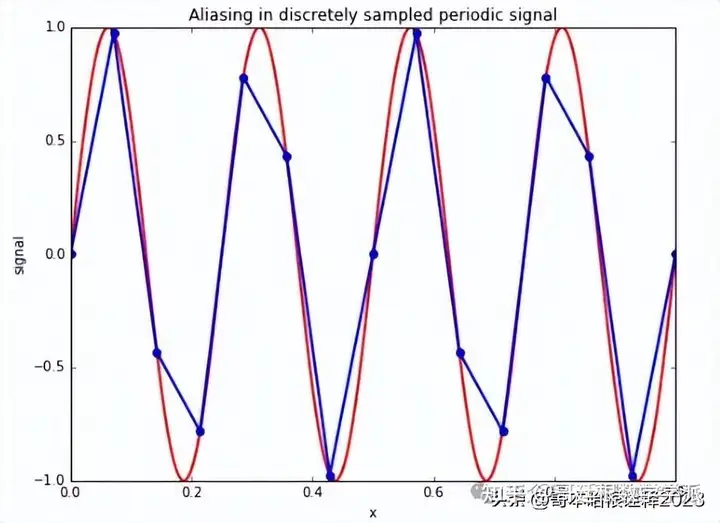
def plot_sine(frequency=4.0, grid_points=12, plot_original=True):
"""
Plot discrete samples of a sine wave on the interval ``[0, 1]``.
"""
x = np.linspace(0, 1, grid_points + 2)
y = np.sin(2 * frequency * np.pi * x)
xf = np.linspace(0, 1, 1000)
yf = np.sin(2 * frequency * np.pi * xf)
fig, ax = plt.subplots(figsize=(8, 6))
ax.set_xlabel('x')
ax.set_ylabel('signal')
ax.set_title('Aliasing in discretely sampled periodic signal')
if plot_original:
ax.plot(xf, yf, color='red', linestyle='solid', linewidth=2)
ax.plot(x, y, marker='o', linewidth=2)
# The interact function automatically builds a user interface for exploring the
# plot_sine function.
interact(plot_sine, frequency=(1.0, 22.0, 0.5), grid_points=(10, 16, 1), plot_original=True);
复制代码
知乎学术咨询:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1