力扣刷题之054.把二叉搜索树转换为累加树

题干描述：

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

复制代码

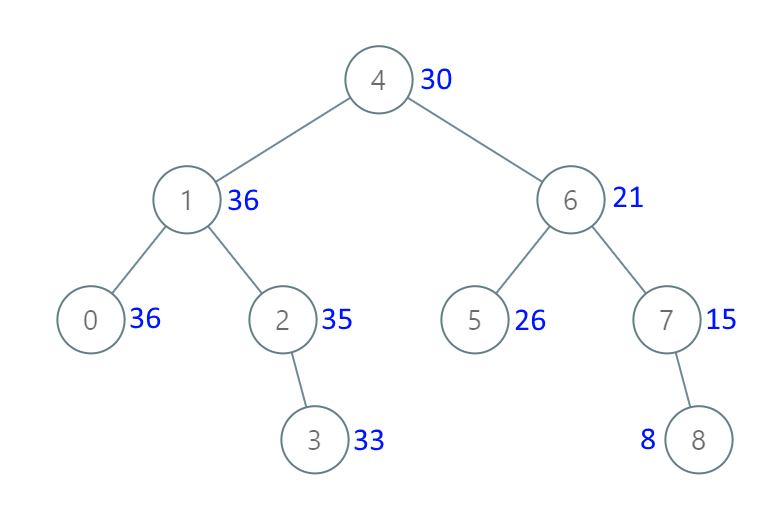
输入：root=[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

复制代码

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

复制代码

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

复制代码

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

题干分析：

因为这道题的题目要求比较简单，所以我们直接对题目理解做出相应的阐述即可：

题干理解：

题干要求就是讲一个二叉搜索树转换为第一个累积和树（即每个节点的值替换为树中大于或等于该节点值的所有节点值之和）。

解题思路：

在正式思考该如何解题之前我们先简单了解一下二叉搜索树的相关性质：

1.左子树节点值 < 根节点值

2.右子树节点值 > 根节点值

3.左右子树也分别是二叉搜索树

为了能够完成二叉搜索树转换为累积和树的相关操作，我们需要遍历树并累加节点值。其中一个有效的方法是使用反向中序遍历（右 -> 根节点 ->左）：使用这种遍历方法能够确保我们先处理较大的节点，再处理较小的节点。同时通过一个累积和变量，再遍历过程中逐步累加节点值并更新当前节点的值。

详细的解题步骤如下：

1.定义树结构体用来表示树的节点

cpp 复制代码

struct TreeNode {
    int val; // 节点值
    struct TreeNode *left; // 左子节点
    struct TreeNode *right; // 右子节点
};

2.反向中序遍历递归并更新节点值

1.定一个递归函数reverseInorderTraversal用于接收数的根节点和一个累积和变量的指针。

2.递归遍历右子树，更新累积和并替换当前节点的值，然后递归遍历左子树。

cpp 复制代码

void reverseInorderTraversal(struct TreeNode* root, int* sum) {
    if (root == NULL) {
        return;
    }

    // 先递归遍历右子树
    reverseInorderTraversal(root->right, sum);

    // 更新累积和并替换当前节点值
    *sum += root->val; // 累加当前节点值到累积和
    root->val = *sum; // 将累积和赋值给当前节点

    // 再递归遍历左子树
    reverseInorderTraversal(root->left, sum);
}

使用sum累加并更新当前节点的值。

3.转换函数

1.定义一个convertBST函数用于初始化累积和变量并调用reverseInorderTraversal用于执行转换。

cpp 复制代码

struct TreeNode* convertBST(struct TreeNode* root) {
    int sum = 0; // 初始化累积和
    reverseInorderTraversal(root, &sum); // 进行反向中序遍历并更新节点值
    return root; // 返回更新后的树的根节点
}

该函数通过初始化sum并调用reverseInorderTraversal函数执行转换。

4.辅助函数

1.定义createNode函数用于创建新的树节点

cpp 复制代码

struct TreeNode* createNode(int val) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->val = val; // 设置节点值
    newNode->left = NULL; // 初始化左子节点为空
    newNode->right = NULL; // 初始化右子节点为空
    return newNode; // 返回新创建的节点
}

2.定义freeTree函数用于递归释放树节点的内存

cpp 复制代码

void freeTree(struct TreeNode* root) {
    if (root != NULL) {
        freeTree(root->left); // 递归释放左子树
        freeTree(root->right); // 递归释放右子树
        free(root); // 释放当前节点
    }
}

3.定义inorderTraversal函数用于打印树的中序遍历结果，用于测试

cpp 复制代码

void inorderTraversal(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }
    inorderTraversal(root->left); // 递归遍历左子树
    printf("%d ", root->val); // 打印当前节点值
    inorderTraversal(root->right); // 递归遍历右子树
}

完整的实现代码如下：

cpp 复制代码

#include <stdio.h>
#include <stdlib.h>

//定义二叉树节点结构
struct TreeNode {
	int val;//定义节点值
	struct TreeNode *left;//左子结点
	struct TreeNode* right;//右子节点
};
//定义一个函数用于反向中序遍历并更新节点值的递归函数
void reverseInorderTraversal(struct TreeNode* root, int* sum) {
	//若根节点为空，则该二叉搜索树为空
	if (root == NULL)
	{
		return;
	}

	//先递归遍历右子树
	reverseInorderTraversal(root->right, sum);
	//更新累积和并替换当前节点值
	*sum += root->val;//累加当前节点值到累积和
	root->val = *sum;//将累积和赋值给当前的节点

	//再递归遍历左子树
	reverseInorderTraversal(root->left, sum);

}
//将二叉搜索树的节点值替换为大于或等于该节点值的所有节点值之和
struct TreeNode* convertBST(struct TreeNode* root) {
	//先将累积和初始化
	int sum = 0;
	//对二叉搜索树进行反向中序遍历并更新节点值
	reverseInorderTraversal(root, &sum);
	//将更新后的树的根节点返回
	return root;

}

//定义一个辅助函数用于创建新的二叉树节点
struct TreeNode* createNode(int val) {
	struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
	//设置节点值
	newNode->val = val;
	//将左右子节点初始为空
	newNode->left = NULL;
	newNode->right = NULL;
	//返回新创建的节点
	return newNode;
}
//定义一个辅助函数用于释放二叉树节点的内存
void freeTree(struct TreeNode* root) {
	if (root != NULL)
	{
		//递归地将左右子树释放掉
		freeTree(root->left);
		freeTree(root->right);
		free(root);
	}
}
//定义一个函数用于打印二叉树的中序遍历
void inorderTraversal(struct TreeNode* root) {
	if (root == NULL)
	{
		return;
	}
	inorderTraversal(root->left); // 递归遍历左子树
	printf("%d ", root->val); // 打印当前节点值
	inorderTraversal(root->right); // 递归遍历右子树
}
// 测试函数
int main() {
	// 创建测试二叉搜索树
	struct TreeNode* root = createNode(4);
	root->left = createNode(1);
	root->right = createNode(6);
	root->left->left = createNode(0);
	root->left->right = createNode(2);
	root->left->right->right = createNode(3);
	root->right->left = createNode(5);
	root->right->right = createNode(7);
	root->right->right->right = createNode(8);

	printf("中序遍历原始二叉搜索树:\n");
	inorderTraversal(root);
	printf("\n");

	// 转换为累积和树
	root = convertBST(root);

	printf("中序遍历转换后的二叉搜索树:\n");
	inorderTraversal(root);
	printf("\n");

	// 释放二叉树内存
	freeTree(root);

	return 0;
}