在高级驾驶辅助系统（ADAS）领域，存在多种常用的坐标系：雷达Lidar坐标系、车辆坐标系、相机坐标系、图像坐标系。
旋转变换矩阵（Rotation M atrix）
在二维平面xoy上，由绿色坐标系逆时针 旋转θ°到蓝色坐标系 。可以看到，点A是没有移动的，变化的是点A分别在前后两个坐标系中的坐标，即从变换到了
。
如图1中黑色虚线的分解方式所示，通过矢量分解 （类似于物理中力、速度等矢量的分解），将绿色坐标系 中的分别分解到蓝色坐标系的x轴和y轴上，可以得到：
用矩阵表示为：
其中R则为二维情形下的旋转变换矩阵，它表示了A点在前后坐标系中的值的映射关系。
三维情形
有了上述在二维平面旋转的基础，三维空间的旋转矩阵也就不难得出了。
即绕x轴，y轴，z轴分别进行旋转。最后将这三个旋转变换矩阵相乘，就能得到在三维空间任意角度的旋转变换矩阵了。（xyz轴满足右手系关系）
在绕x轴 旋转的时候，可以看作在yoz二维平面上的旋转，此时x的值不变。
在绕y轴 旋转的时候，可以看作在zox二维平面上的旋转，此时y的值不变。
在绕z轴 旋转的时候，可以看作在xoy二维平面上的旋转，此时z的值不变。
最终的三维旋转变换矩阵就是上面三个矩阵相乘，意为三维坐标系分别绕x轴、y轴和z轴旋转相应的角度。
正交矩阵
向量正交
首先先明白什么是在解析几何中的概念，向量正交是指：若两个同维向量
的点乘（也叫：数量积）为0，则两个向量正交（也叫垂直），即：在平面直角坐标系中 
相互垂直（夹角为90度）。
例：假设存在三个向量，分别为：
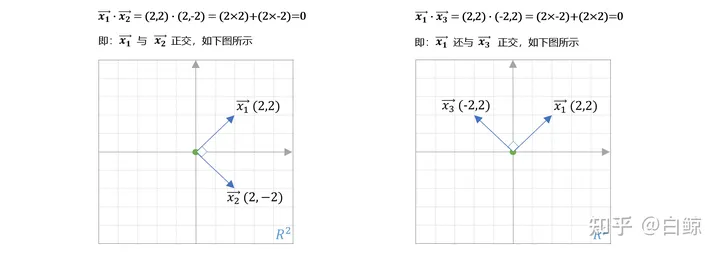
正交矩阵
如果把正交的向量，按列向量的形式放进一个花括号内，即组成了一个正交向量组。那么该正交向量组中的向量，均两两相互垂直（也就是任意拿出两个向量来做点乘都=0）。
例：假设存在4个向量，分别为： 
正交基
基向量是构成向量空间的一个向量组（坐标系），该向量组内的向量是线性无关的（若两两正交，则必定线性无关），并且通过它们的线性组合可以表示整个向量空间中的任意向量。
在此基础上，若基向量组内的向量两两正交，则称作：正交基，如下图所示：
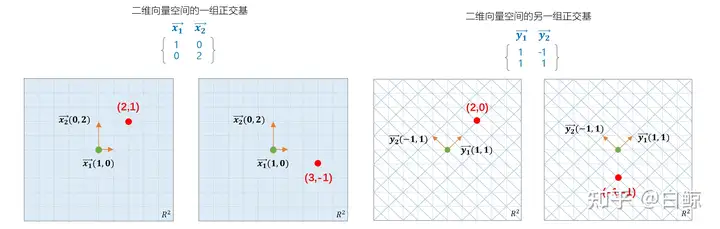
特别的：若基向量组内的向量两两正交，且向量长度均为1，则称作：标准正交基。
向量组转矩阵
矩阵是一种数据结构，简单来说就是一张数表，往格子里填入相应的数字就能视作一个矩阵，所以向量组可以视作矩阵。那么，我们把上面的正交向量组视作矩阵：
正交矩阵
当正交向量组转为矩阵后，我们就可以用矩阵的视角来重新看待"正交向量组"
例1：是几行几列的矩阵？是不是方阵？
例2：矩阵的秩是多少？矩阵是否可逆？
至此，最核心的问题是：什么样的矩阵才能称作正交矩阵？
第一点：必须是一个方阵，即n行n列；
第二点：矩阵中的每一列若视作向量，则这些向量均两两相互垂直；
第三点**：矩阵中的每一列若视作向量，则这些向量的长度均为1；**
同时满足这3点，即为一个正交矩阵。让我们来看一些例子：
数学定义及性质
1、数字定义：
若一个方阵
是正交矩阵，当且仅当它的转置矩阵与自身的乘积等于单位矩阵
另一种等价的定义是：若方阵是正交矩阵，当且仅当的列向量是两两正交的单位向量。
2、数学特性
1、正交矩阵的逆：
，正交矩阵的转置 = 正交矩阵的逆
2、正交矩阵的行列式： 行列式的取值只有两种可能（1）或（-1）
3、向量正交：将
视作由若干行向量组成，则这些行向量两两相互正交，若将视作由若干列向量组成，则这些列向量也两两相互正交