FPGA图像处理之均值滤波

爱奔跑的虎子2024-10-19 11:39

文章目录

一、什么是图像滤波？

图像滤波是一种图像处理技术，旨在通过对图像进行修改来改善图像质量或提取特定特征。滤波通常用于去除噪声、平滑图像、增强边缘或提取特征等。

1.1 噪声类型

在图像数据采集、处理、传输等过程中图像数据会受到噪声损坏；因为噪声无处不在，严重的会直接影响用户视觉感受，因此在图像处理中降噪是非常关键的步骤，对于不同类型的噪声使用不同的滤波器会有更好的效果。以下是被不同类型噪声污染的图片，matlab代码：

matlab 复制代码 
% 读取原始图像
originalImage = imread('yuanyang.bmp'); % 替换为你的图像文件名

% 将图像转换为灰度图像（如果是彩色图像）
if size(originalImage, 3) == 3
    originalImage = rgb2gray(originalImage);
end

% 添加高斯噪声
gaussianNoiseImage = imnoise(originalImage, 'gaussian', 0, 0.01); % 均值0，方差0.01

% 添加椒盐噪声
saltPepperNoiseImage = imnoise(originalImage, 'salt & pepper', 0.02); % 2% 椒盐噪声

% 添加泊松噪声
poissonNoiseImage = imnoise(originalImage, 'poisson');

% 添加斑点噪声
speckleNoiseImage = imnoise(originalImage, 'speckle', 0.04); % 方差0.04

% 显示原始图像和不同类型的噪声图像
figure;

subplot(2, 3, 1);
imshow(originalImage);
title('原始图像');

subplot(2, 3, 2);
imshow(gaussianNoiseImage);
title('高斯噪声');

subplot(2, 3, 3);
imshow(saltPepperNoiseImage);
title('椒盐噪声');

subplot(2, 3, 4);
imshow(poissonNoiseImage);
title('泊松噪声');

subplot(2, 3, 5);
imshow(speckleNoiseImage);
title('斑点噪声');
  1. 高斯噪声：服从高斯分布的随机噪声，通常表现为图像的亮度随机波动；通常由传感器噪声或其他随机因素引起。
  2. 椒盐噪声：图像中随机出现的黑色和白色像素，类似于撒盐和胡椒；通常由图像传输错误或传感器有坏点引起的。
  3. 泊松噪声：与光子计数相关的噪声，通常在低光照条件下出现；常见于医学成像和天文成像，在低亮度区域，噪声会显得更加明显。
  4. 斑点噪声：通常在医学影像中出现，表现为图像中的随机斑点。

1.2 滤波类型

图像滤波通常涉及对图像中每个像素的值进行修改，通常是通过考虑该像素及其邻域像素的值。滤波器通常使用一个称为"卷积核"或"滤波器"的小矩阵来实现这一点。卷积核在图像上滑动，并对覆盖的像素值进行加权平均或其他运算，常见的图像滤波器有：

  1. 均值滤波器
  2. 高斯滤波器
  3. 中值滤波器
  4. 双边滤波器
  5. 拉普拉斯滤波器
  6. Sobel滤波器
  7. Canny滤波器

不同滤波器对应的应用场景也不同，有的是做降噪，有的是提取图像特征，本篇文章先来介绍均值滤波器的实现。

二、均值滤波原理

我们知道图像滤波就是通过判断当前像素周边的像素来修改，可以想象成一个矩形框。所以滤波关键的因素就是矩形框的大小以及矩形框里的像素值所占的权重。均值滤波的原理：就是用矩形框里面所有的像素值的平均值来替换矩形框中心的像素，如下图所示，表示一幅图像数据：

上面是一幅10*6 大小的图像数据，假如这幅图像数据被椒盐噪声污染，我们污染后的像素点标志为红色，如下图所示：

这些噪点在视觉上表现为亮度特别突出的点，比周围像素点的亮度高很多，因此才会影响到视觉效果。均值滤波的计算窗口有 33 、5 5、77等等，窗口越大计算量越大，效果也越好，这里用33的窗口来演示均值滤波。

2.1 3*3窗口滑动过程

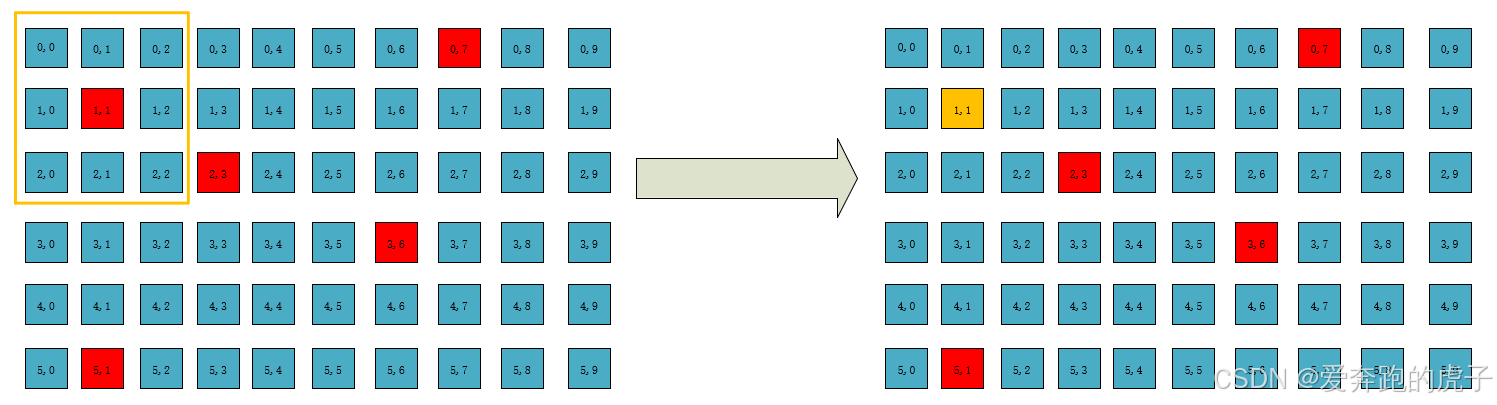
第一个3*3窗口从上到下，从左到右依次滑动，每次滑动窗口后计算并且修改中心值的像素值。如上图所示第一次窗口滑动计算了这9个像素的均值然后替换了中心点的像素值，这样第一个噪点就被平均了，不会那么突出了。这也是均值滤波的局限性，噪声并没有被消除而是被平均了；如果窗口很大，那么图片也会变得有点模糊，也会平滑图像的边缘特征。

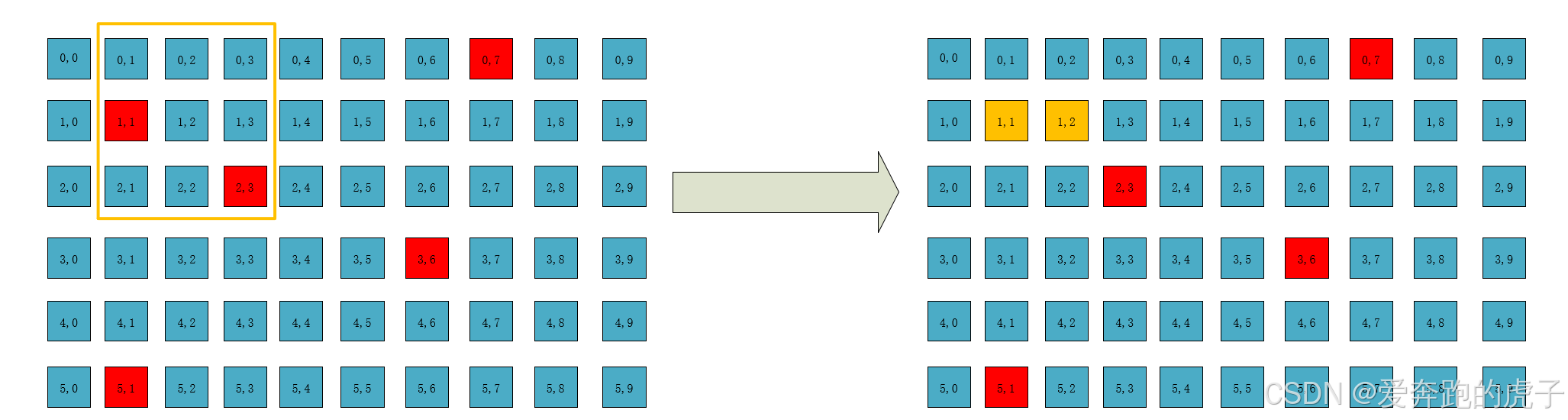
第二个窗口滑动后，计算替代了（1，2）的像素点，其它的以此类推。

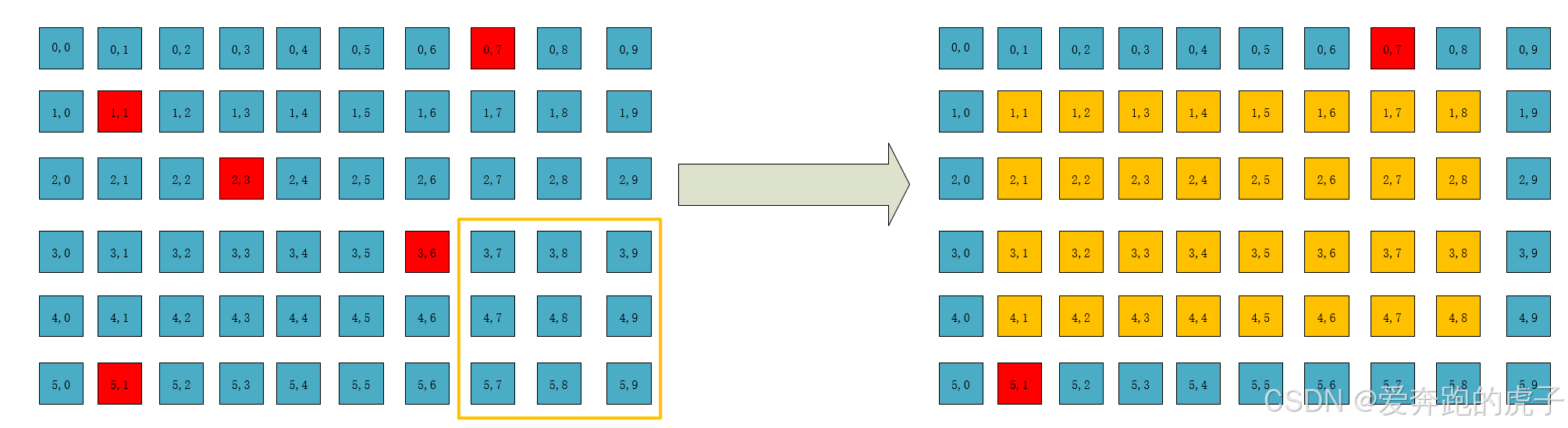
上图是窗口滑动到最后一行后，我们可以看到在经过33窗口滑动计算后，新的图像会少两行两列；如果是55的窗口，滑动后会少4行4列，因此在实际处理过程中需要对图像进行扩展来确保计算后的图像大小不变。

2.2 图像扩展

通常图像扩展会通过补0或者补1，或者使用原值来填充，这里我们使用原值填充，就是判断当前计算的点为边缘时，不用计算直接用原值填充就行，我们需要在原始图像进行扩展2行2列，如下图所示：

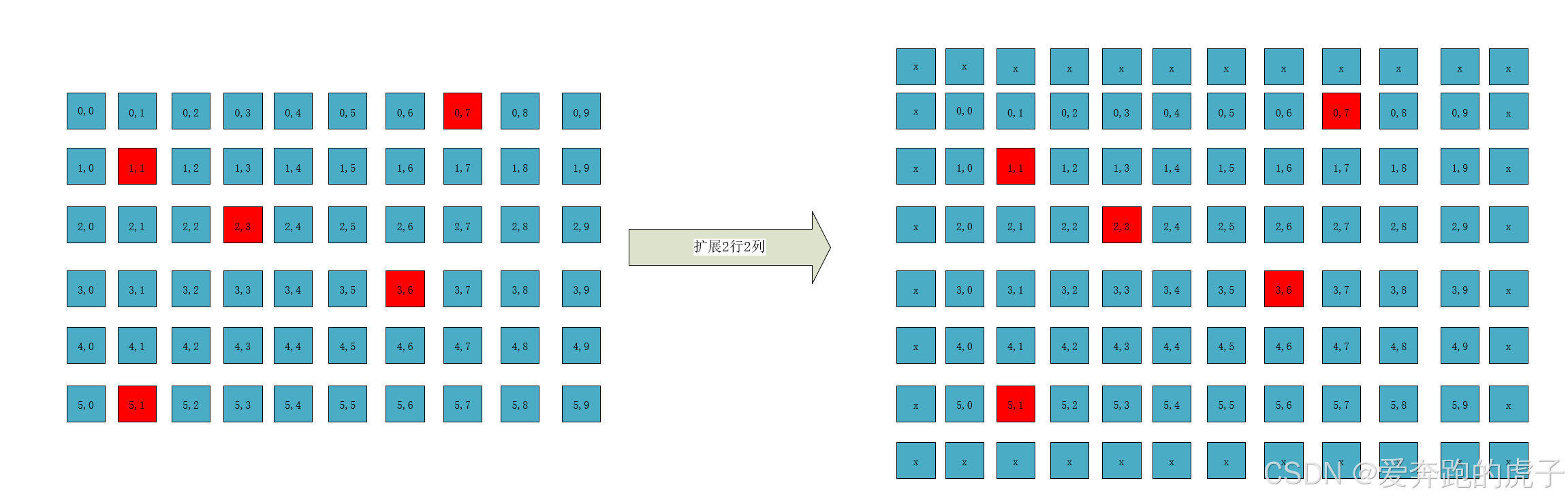
如上所示，我们用x值来填充原始图像，假如原始图像大小为NM，那么填充后的图像大小为(N+2) * (M+2)，我们再用新的图像大小做33窗口的滑动，如下所示：

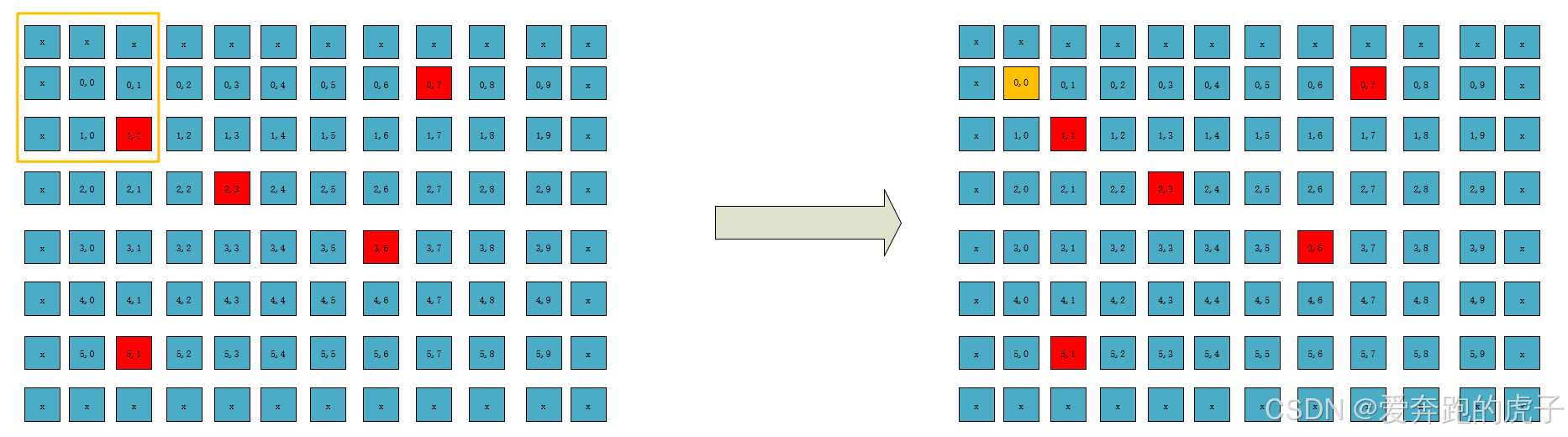
第一次窗口滑动后计算了新图像左上角的像素。

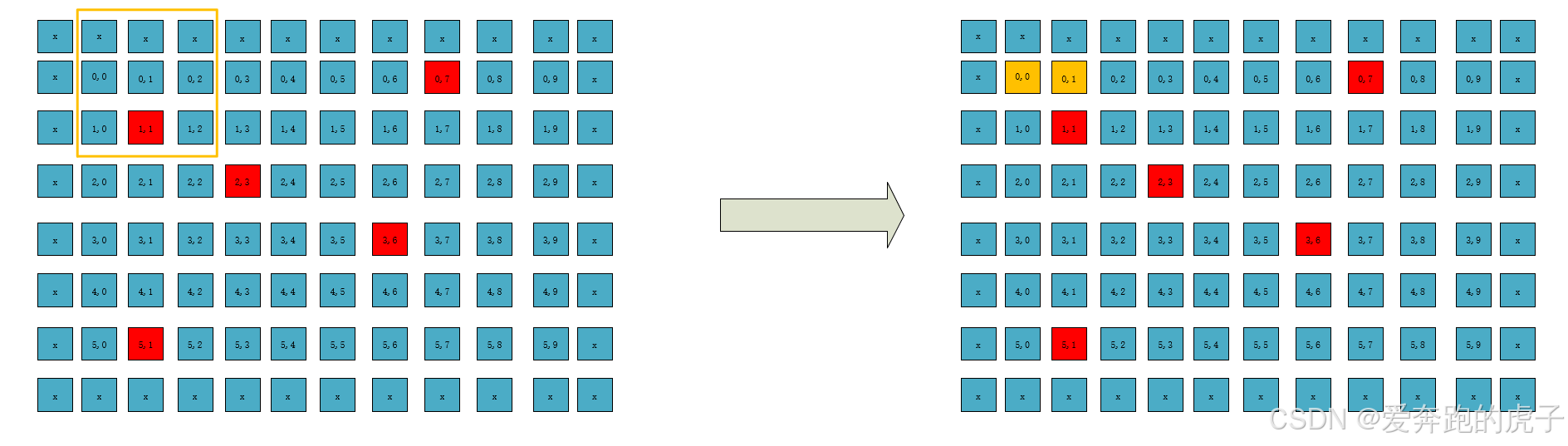
第二次窗口滑动计算了新图像的第一行左边第二个的像素，其它的依次类推。

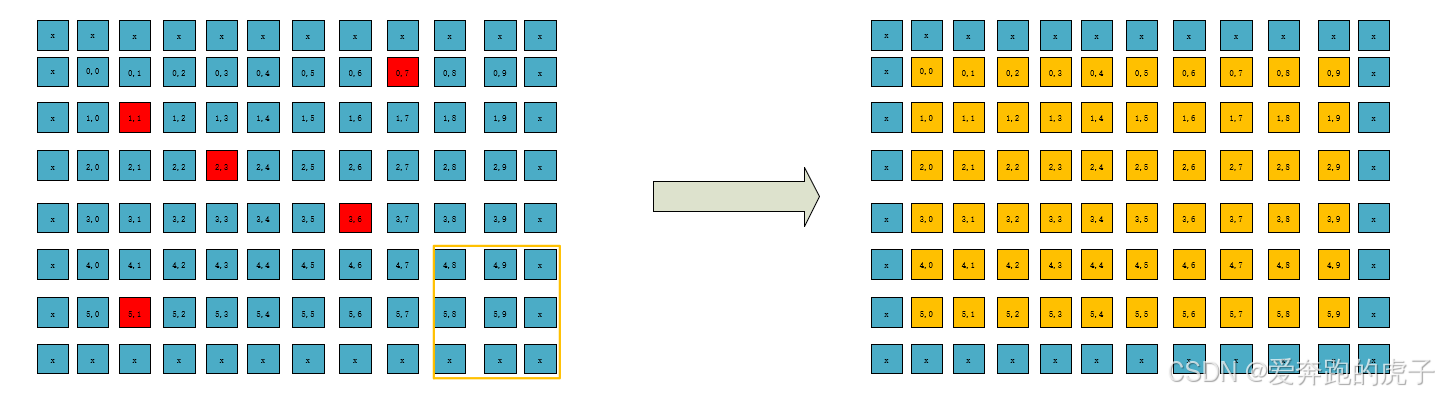
在滑动完最后一个窗口后，图像也就计算完成。原始图像大小为 NM 经过图像扩展变成 (N+2) * (M+2)，再经过33窗口计算变成了 N*M，这样新的图像大小就和原始图像大小一致了。

三、Matlab实现均值滤波

在Matlab里可以直接调用均值滤波的函数，再滤波之前需要将图像数据转成灰度图像，因为噪声污染的大多是是异常的亮度，跟颜色无关，在均值的时候也是平均亮度，matlab代码如下：

matlab 复制代码 
clc;
close all;
% 读取原始图像
originalImage = imread('yuanyang.bmp'); 

% 将图像转换为灰度图像（如果是彩色图像）
if size(originalImage, 3) == 3
    originalImage = rgb2gray(originalImage);
end

% 添加噪声
noisyImage = imnoise(originalImage, 'salt & pepper', 0.02); % 添加椒盐噪声

% 均值滤波
filterSize = 3; % 滤波器大小
meanFilteredImage = imfilter(noisyImage, fspecial('average', filterSize));

% 显示原始图像、带噪声的图像和均值滤波后的图像
figure;

subplot(1, 3, 1);
imshow(originalImage);
title('原始图像');

subplot(1, 3, 2);
imshow(noisyImage);
title('带噪声的图像');

subplot(1, 3, 3);
imshow(meanFilteredImage);
title('均值滤波后的图像');

我们放大滤波后的图像来看。

可以看到噪点其实都没有被消除，只是被平均了而已，这也是均值滤波的局限性。我们把窗口设成5*5，再放大看一下。

可以看到窗口变大后，降噪效果也变好了，但是图像变得模糊了。

四、FPGA实现均值滤波

实现均值滤波的关键就是开窗和扩展，关于生成3*3的矩阵，我们可以参考《FPGA图像处理之三行缓存》这里面，稍作修改一下。

4.1 生成 3*3 矩阵

我们在三行缓存的基础上增加两行两列，使得原图像扩展一下，最后通过一个3*3的矩阵依次缓存下来：

c 复制代码 
always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)begin
        {ro_matrix_11, ro_matrix_12, ro_matrix_13} <= 'd0;
        {ro_matrix_21, ro_matrix_22, ro_matrix_23} <= 'd0;
        {ro_matrix_31, ro_matrix_32, ro_matrix_33} <= 'd0;
    end
    else if(w_img_data_valid == 1'b1)begin
        {ro_matrix_11, ro_matrix_12, ro_matrix_13} <= {ro_matrix_12, ro_matrix_13,w_img_data_1line};
        {ro_matrix_21, ro_matrix_22, ro_matrix_23} <= {ro_matrix_22, ro_matrix_23,w_img_data_2line};
        {ro_matrix_31, ro_matrix_32, ro_matrix_33} <= {ro_matrix_32, ro_matrix_33,w_img_data_3line};
    end
end

4.2 仿真3*3矩阵

为了加快我们的仿真时间，我们在tb文件里先设置图像的长宽为50*50，然后输入的图像数据为0、1、2、3、...2499。仿真代码如下：

c 复制代码 
`timescale 1ns / 1ps

module tb_img_3line_buffer();

reg                                                 sys_clk ;
reg                                                 sys_rst ;
reg                                                 i_img_data_valid    ;
reg             [23:0]                              i_img_data  ;
reg             [12:0]                              cnt ;
reg             [1:0]                               waite_cnt   ;



initial begin
    sys_clk =0;
    sys_rst = 1;
    i_img_data_valid = 0;
    i_img_data = 'd0;
    #200;
    sys_rst = 0;
end

always #5 sys_clk = ~sys_clk;

always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)
        waite_cnt <= 'd0;
    else if(cnt == 49)
        waite_cnt <= 'd0;
    else if(i_img_data_valid == 1'b0)
        waite_cnt <= waite_cnt + 1'b1;
    else
        waite_cnt <= waite_cnt;
end

always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)
        i_img_data_valid <= 1'b0;
    else if(cnt == 49)
        i_img_data_valid <= 1'b0;
    else if((waite_cnt == 3) && (i_img_data <= 2499))
        i_img_data_valid <= 1'b1;
    else
        i_img_data_valid <= i_img_data_valid;
end

always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)
        cnt <= 'd0;
    else if(cnt == 49)
        cnt <= 'd0;
    else if(i_img_data_valid == 1'b1)
        cnt <= cnt + 1'b1;
    else
        cnt <= cnt;
end

always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)
        i_img_data <= 'd0;
    //else if(i_img_data == 49)
    //    i_img_data <= 'd0;
    else if(i_img_data_valid == 1'b1)
        i_img_data <= i_img_data + 1'b1;
    else
         i_img_data <= i_img_data;
end

endmodule

在代码里，我设置的扩展行列数据用十进制66填充，这样为了更好的观察，实际上可以根据需要任意填充数据。

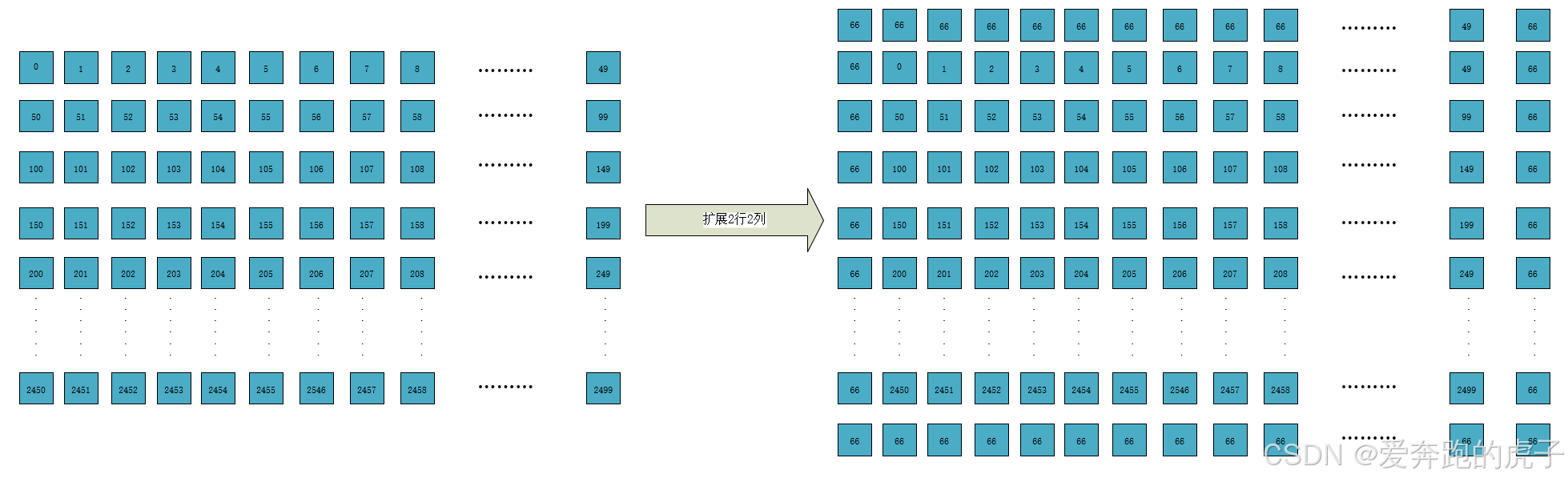
仿真输入的图像数据如上所示。

读出的矩阵数据应该如上所示，第一个矩阵的数据从上到下，从左到右应该是：66、66、66、66、0、1、66、50、51；第二个矩阵数据应该是：66、66、66、0、1、2、50、51、52；其他的以此类推。我们打开仿真：

  我们可以看到输入的图像数据就是从0-2499的累加数，每一行50个数，一共50列，我们来看输出的矩阵：

第一个矩阵是66、66、66、66、0、1、66、50、51；第二个矩阵数据是：66、66、66、0、1、2、50、51、52；和我们设定的一致，其他的也是一样。

4.3 计算均值

均值计算比较简单，就是九个数据相加起来除以9。我们知道FPGA不擅长做除法，因此我们可以先扩大再截位，可以先把数据扩大2^15 / 9 = 3640。然后取高8位即可，Verilog代码如下：

c 复制代码 
always @(posedge sys_clk) begin
    if(sys_rst == 1'b1)begin
        sum_1_line  <= 'd0;
        sum_2_line  <= 'd0;
        sum_3_line  <= 'd0;
        all_sum     <= 'd0;
    end
    else begin
        sum_1_line  <= w_matrix_11[23:16] + w_matrix_12[23:16] + w_matrix_13[23:16];
        sum_2_line  <= w_matrix_21[23:16] + w_matrix_22[23:16] + w_matrix_23[23:16];
        sum_3_line  <= w_matrix_31[23:16] + w_matrix_32[23:16] + w_matrix_33[23:16];
        all_sum     <= sum_1_line + sum_2_line + sum_3_line;
    end
end

//延迟了1拍，avg = all_sum / 9 = all_sum * 3641 >> 15
always @(posedge sys_clk) begin
    if(sys_rst)
        sum_mult <= 'd0;
    else
        sum_mult <= all_sum * 12'd3641;
end

//延迟了1拍
always @(posedge sys_clk) begin
    if(sys_rst)
        agv_data <= 'd0;
    else
        agv_data <= sum_mult[22:15] + sum_mult[14];    //四舍五入
end

4.4 仿真均值滤波

我们先用matlab给一张图片加上椒盐噪声然后生成灰度图片，matlab代码如下：

matlab 复制代码 
% 读取原始灰度图像
originalImage = imread('your_image.jpg'); % 替换为你的图像文件名

% 检查图像是否为灰度图像
if size(originalImage, 3) == 1
    % 如果是灰度图像，直接使用
    grayImage = originalImage;
else
    % 如果是彩色图像，转换为灰度图像
    grayImage = rgb2gray(originalImage);
end

% 将灰度图像转换为 24 位 RGB 图像
rgbImage = cat(3, grayImage, grayImage, grayImage);

% 添加椒盐噪声（可以根据需要选择其他类型的噪声）
noisyImage = imnoise(rgbImage, 'salt & pepper', 0.02); % 2% 椒盐噪声

% 保存带噪声的图像为 24 位 BMP 文件
imwrite(noisyImage, 'noisy_image.bmp'); % 保存为 noisy_image.bmp

% 应用均值滤波
filteredImage = imfilter(noisyImage, fspecial('average', [3 3]), 'replicate');

% 显示原始图像、带噪声的图像和均值滤波后的图像
figure;

subplot(1, 3, 1);
imshow(rgbImage);
title('原始灰度图像（RGB）');

subplot(1, 3, 2);
imshow(noisyImage);
title('带噪声的图像');

subplot(1, 3, 3);
imshow(filteredImage);
title('均值滤波后的图像');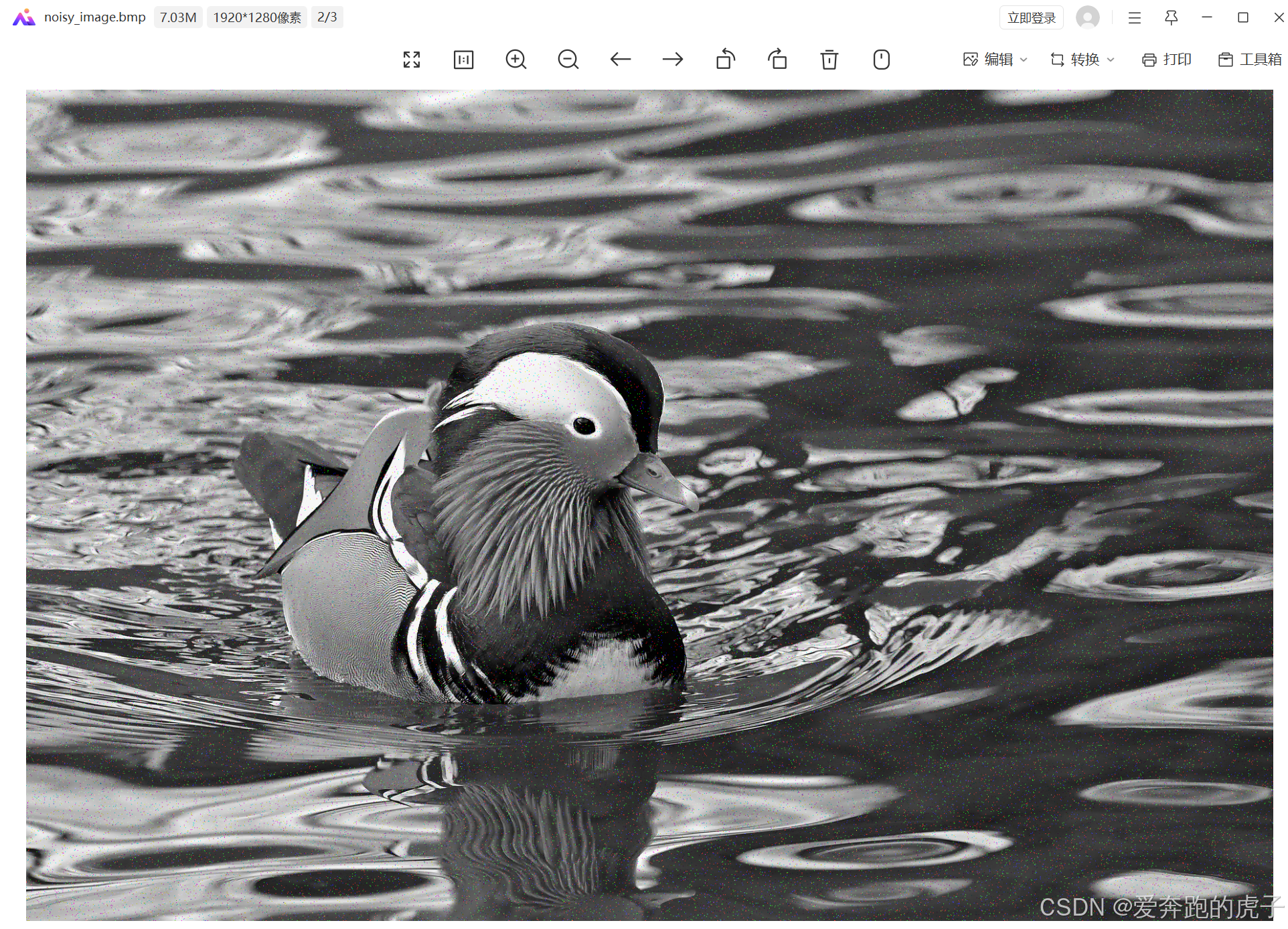

生成图片后，我们输入到仿真里面，添加均值滤波模块然后启动仿真。

我们可以看到噪点被滤波处理变得暗淡了，我们放大看一些细节。

放大后的图像依然有噪点，和matlab仿真放大的几乎一样，这就说明均值滤波不适合滤掉椒盐噪声，后续还会讲到其它滤波算法。

相关推荐
li星野8 小时前
打工人日报#20251005
笔记·程序人生·fpga开发·学习方法
通信小呆呆9 小时前
FPGA 上的 OFDM 同步：从 S&C 到残差 CFO 的工程化实现
fpga开发·信号处理·同步·ofdm
2401_8414956410 小时前
【计算机视觉】分水岭实现医学诊断
图像处理·人工智能·python·算法·计算机视觉·分水岭算法·医学ct图像分割
listhi52012 小时前
基于MATLAB的高斯混合模型（GMM）实现
开发语言·matlab
格林威13 小时前
常规可见光相机在工业视觉检测中的应用
图像处理·人工智能·数码相机·计算机视觉·视觉检测
扶尔魔ocy15 小时前
【QT常用技术讲解】multimedia实现指定分辨率打开摄像头
图像处理·qt
格林威17 小时前
工业视觉检测里的 “柔性” 是什么？
图像处理·人工智能·深度学习·yolo·计算机视觉·视觉检测
格林威19 小时前
不同光谱的工业相机有哪些？能做什么？
图像处理·人工智能·深度学习·数码相机·计算机视觉·视觉检测
CiLerLinux20 小时前
第三十八章 ESP32S3 SPIFFS 实验
图像处理·人工智能·单片机·嵌入式硬件
hahaha601620 小时前
高层次综合基础-vivado hls第三章
算法·fpga开发
热门推荐
01KGG转MP3工具|非KGM文件|解密音频02BongoCat - 跨平台键盘猫动画工具03jdk21下载、安装（Windows、Linux、macOS）04GitHub 镜像站点05UV安装并设置国内源06HarmonyOS NEXT开发进阶（十四）：HarmonyOS应用开发者基础认证试题集汇总及答案解析07adb安装教程（附adb命令大全详解）adb环境配置教程08零基础搭建赛博朋克个人主页：蓝耘Claude Code完整实战教程0946个Nano-banana 精选提示词，持续更新中10Linux下V2Ray安装配置指南