力扣二叉树的最大深度

树的遍历，dfs与bfs基础。

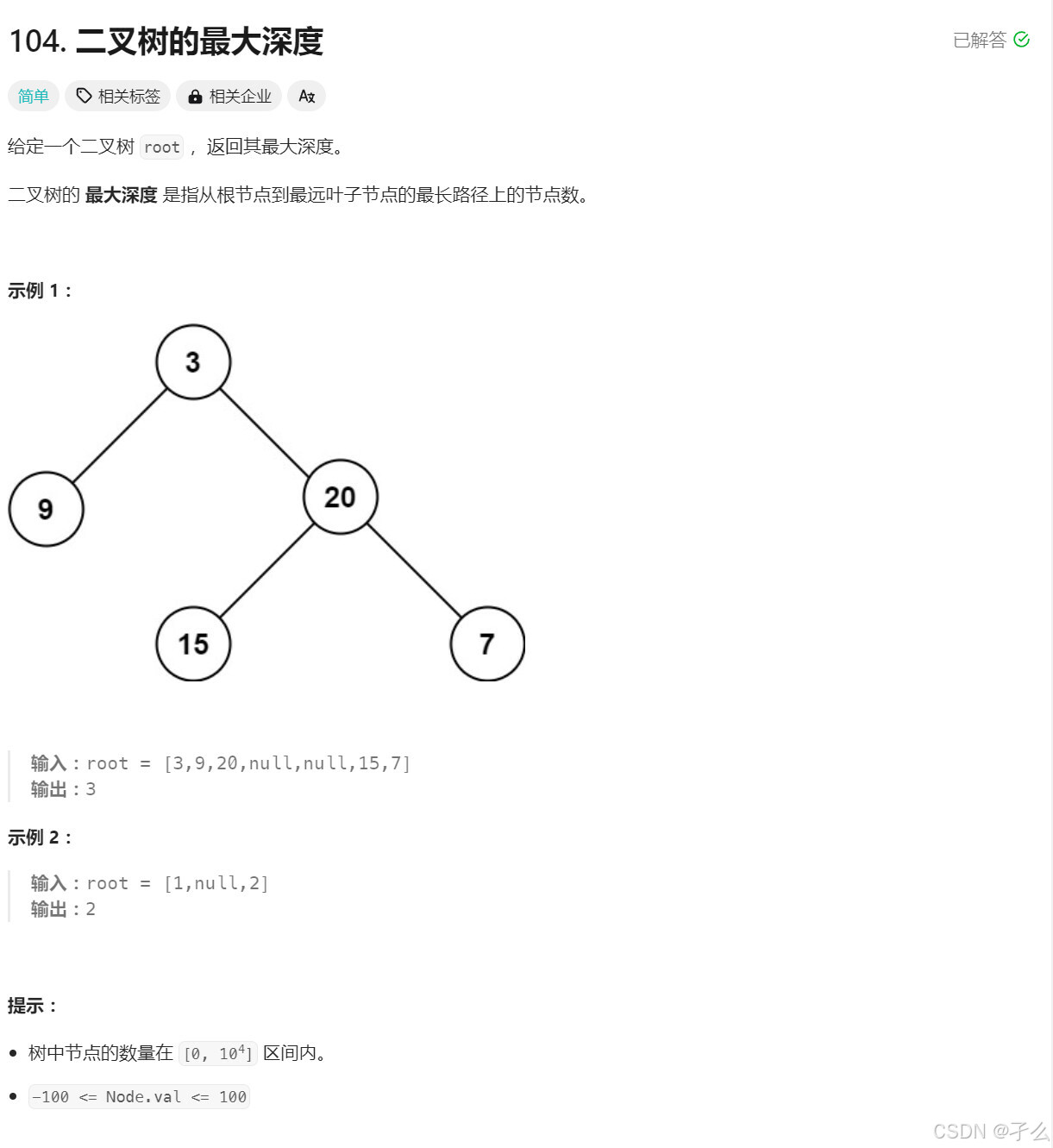
注意这种题要看根节点的深度是0还是1。

深度优先遍历dfs，通过递归分别计算左子树和右子树的深度，然后返回左右子树深度的最大值再加上 1。递归会一直向下遍历树，直到达到叶子节点或空节点。在回溯过程中，计算每一层的深度并返回，最终求得整棵树的最大深度。

时间复杂度：O(n)，空间复杂度：O(n)（最坏情况）或 O(log n)（最佳情况）。

java 复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

广度优先遍历bfs，逐层遍历，从树的第一层开始，逐渐访问下一层。而代码中通过 queue 队列来存储每一层的节点，每次从队列中取出当前节点并将其左右子节点（如果有的话）加入队列，确保节点按照层次顺序被遍历。下一层的节点会在当前层的节点都处理完之后，才开始被访问。

时间复杂度是 O(n)，空间复杂度是O(n)。

java 复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public static int maxDepth(TreeNode root) {
        if (root == null) return 0;  // 如果树为空，深度为0
        
        Queue<TreeNode> queue = new LinkedList<>();  // 使用队列
        queue.add(root);  // 将根节点加入队列
        
        int depth = 0;  // 用来记录深度
        
        while (!queue.isEmpty()) {  // 当队列不为空时继续遍历
            int size = queue.size();  // 当前层节点的数量
            for (int i = 0; i < size; i++) {  // 遍历当前层的每个节点
                TreeNode node = queue.poll();  // 从队列头部移除节点
                if (node.left != null) queue.add(node.left);  // 如果左子树存在，加入队列
                if (node.right != null) queue.add(node.right);  // 如果右子树存在，加入队列
            }
            depth++;  // 当前层处理完后，深度加1
        }
        
        return depth;  // 返回最大深度
    }
}

力扣 二叉树的最大深度

力扣二叉树的最大深度