【数据结构】励志大厂版·初阶（复习+刷题）单链表

前引：此篇文章作为小编复习的记录，将快速回忆单链表的知识点，讲解单链表增删查找的实现，每个细节之处要注意的地方，解释为何这样设计。文章末尾包含了单链表算法题，同样解释详细，借助题目再次巩固知识点，挑战实战应用，喜欢的伙伴们可以作为大家的复习资料，希望可以给个免费的一键三连哦！正文开始~

知识点速览

[链表 OJ（1）](#链表 OJ（1）)

知识点速览

链表较顺序表而言的优点是地址不连续、空间利用率很高，同样属于线性结构，它的空间是一个个结构体，既可以存储数据，也通过指针存储下一个结构体的地址，实现链式结构，如下抽象理解：

单向不带头非循环链表是最简单的一种链表结构，单链表的实现，需要一个头指针指向第一个节点，然后再后面一个接一个的开辟其它节点，这里下面实现的时候再详细说，下面看看经常说的几个链表名词是哈意思：

单链表结束标志：最后一个节点的指针的next指向空（NULL）

头指针：一个结构体类型的指针，用来指向链表的第一个节点

头节点：在第一个节点之前再连接一个节点，通常可以称为哨兵节点，如下图：

带头节点：头指针指向头节点

不带头节点：头指针指向第一个节点

逻辑结构：比如这里我们将链表想象成了一节一节的样子，通过指针连接，在实际操作中方便理解

物理结构：比较严谨，链表的物理结构是下面这样的，上一个节点存放下一个节点的地址

拓展：指针指向的是地址，是数据具有多个字节的第一个字节的地址（每个字节都有一个地址）

单链表实现

定义结构体

每个链表的节点空间其实是一个结构体，下面我们构建链表节点空间，这个结构体里面有一个指针（用来指向下一个节点的地址），一个数据域（用来存储数据）

cpp 复制代码

typedef int Plastic;

typedef struct List
{
	//结构体指针
	struct List* next;
	//数据域
	Plastic data;
}List;

初始化

我们知道链表有一个头指针（结构体类型），用来指向链表的第一个节点，开始还没有开辟节点，所以它的指向应该是空（NULL）

cpp 复制代码

List* pphead = NULL;

在整个链表中，我们都需要注意以下几点，小编都帮大家整理出来了！希望可以支持一下小编哦

（1）如果需要改变头指针的位置，就传指针地址，采用二级指针接收

如果不需要改变头指针的位置，就传指针，采用一级指针接收

**例如：**我们头插的时候，需要让头指针指向第一个节点，就需要改变头指针位置

（2）链表不存在：我们判断一个链表存不存在，是看它的头指针存不存在

链表为空：链表为空不代表链表不存在，只是里面没有插入节点，只有一个头指针指NULL

例如： 二级指针，pphead==NULL ，就表示这个链表不存在；*pphead==NULL，为空链表

开辟节点

这里为了后面方便，考虑到需要多次开辟节点，我们将它单独设置在一个函数，开辟之后根据常规流程，需要判断空间的有效性，其次是需要初始化空间，如下：

cpp 复制代码

//开辟节点
List* Newnode(int data)
{
	//开辟新节点
	List* newnode = (List*)malloc(sizeof(List));

	if (newnode == NULL)
	{
		printf("开辟失败\n");
		return NULL;
	}

	//初始化节点内容
	newnode->next = NULL;
	newnode->data = data;

	return newnode;
}

尾插

尾插的步骤是先找尾，再插入。如何找尾？新定义一个指针从链表头部开始一个个遍历，直到它的下一个是空，然后将新开辟的节点连接在这个指针的后面，例如我现在定义了一个指针cur ：

为什么判断条件是" cur->next ！= NULL "？

假设，如果cur！=NULL，那么此时cur已经走到了链表的末尾，也就是"NULL"处，如果接下来要插入新节点，那么表示"NULL->next ==新节点"，这样很明显是错误的方式。下面看尾插结果：

cpp 复制代码

//尾插
void Tail_insert(List** pphead,int data)
{
	//看链表存不存在
	assert(pphead);

	//如果是空链表
	if (*pphead == NULL)
	{
		*pphead = Newnode(data);
		return;
	}

	//设置新指针，指向链表开头
	List* cur = *pphead;
	//找尾
	while ((cur->next) != NULL)
	{
		cur = cur->next;
	}
	//找到之后进行插入
	cur->next = Newnode(data);
}

头插

头插我们不需要去找头，因为头指针所指的节点就是该链表的第一个节点，那么如何头插？如下图

先设置一个指针，让其下一个节点是 pphead 指向原先的第一个节点，然后再更新 pphead 指向

cpp 复制代码

//头插
void Head_insert(List** pphead,int data)
{
	//判断链表是否存在
	assert(pphead);
	//如果是空链表
	if (*pphead == NULL)
	{
		*pphead = Newnode(data);
		return;
	}

	//开辟节点
	List* cur = Newnode(data);
	//设置前后关系
	cur->next = *pphead;
	//更新头指针指向
	*pphead = cur;
}

尾删

尾删肯定需要先遍历找尾，找尾的条件应该是"cur->next ！= NULL"

其次还需要找到 cur 的前面一个节点，因为尾删之后，我们需要释放尾部节点，然后尾部前面的节点关系应该是prev->next==NULL。如果未重新确立next的关系，链表就出问题了，如下图理解：

cpp 复制代码

//尾删
void Tail_deletion(List* pphead)
{
	//判断空链表
	assert(pphead);

	List* cur = pphead;
	List* prev = pphead;
	//找尾
	while (cur->next != NULL)
	{
		prev = cur;
		cur = cur->next;
	}
	//释放
	free(cur);
	cur = NULL;
	//改变尾部关系
	prev->next = NULL;
}

头删

头删需要先找到当前头指针指向节点的下一个节点，然后对头指针所指向的节点释放，再更新头指针（如果先更新再释放，那么我们就找不到原来的第一个节点了，切记！）

头删之前

头删之后

cpp 复制代码

//头删
void Head_deletion(List** pphead)
{
	//判断链表释放存在
	assert(pphead);
	//判断空链表
	assert(*pphead);

	//如果只有一个节点
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
		return;
	}
	//先找到第二个节点
	List* cur = (*pphead)->next;
	//释放头指针所指向的节点
	free(*pphead);
	//更新头指针指向
	*pphead = cur;
}

在指定位置之前插入

我们先来看图

这里同尾删一样，需要两个指针，一个找指定位置，一个找指定位置的前一个位置，再来确立next的关系即可。这里不需要去改变头指针的位置，所以使用一级指针就可以！

下面我们来看看插入前与插入后的效果

cpp 复制代码

//在指定位置前插入
void Before_position(List** pphead, int data)
{
	//判断链表是否存在
	if (pphead == NULL)
	{
		return;
	}

	//如果是头插
	if (data == (*pphead)->data)
	{
		Head_insert(pphead, 5);
		return;
	}

	List* cur = pphead;
	List* prev = pphead;
	//找指定位置
	while (cur->data != data)
	{
		prev = cur;
		cur = cur->next;
	}
	//插入节点、设置关系
	prev->next = Newnode(5);
	prev->next->next = cur;
}

在指定位置之后插入

在指定位置后面插入还是需要另外定义两个指针，先标记cur->next的节点，插入之后方便连接

插入前插入后的效果展示

cpp 复制代码

//在指定位置后插入
void Behind_position(List* pphead, int data)
{
	//判断空链表
	if (pphead == NULL)
	{
		return;
	}

	List* cur = pphead;
	List* pc = cur->next;
	//找指定位置
	while (cur->data != data)
	{
		cur = cur->next;
	}
	//插入
	cur->next = Newnode(6);
	//连接（确认next的关系）
	cur->next->next = pc;
}

链表 OJ（1）

**首先跟随小编来分析一下这个题目：**此题是将一个无头单向不循环链表进行翻转，原来的首尾全部倒置过来，需要考虑到链表为空、是否越界的情况，以上就是简单的分析，下面进行思路讲解

思路讲解：

（1）反转链表，我们实际上是反转它的箭头指向。这题我们肯定要记录它的下一个节点。因此避免越界，我们应该先进行判断，防止空链表和一个节点的情况

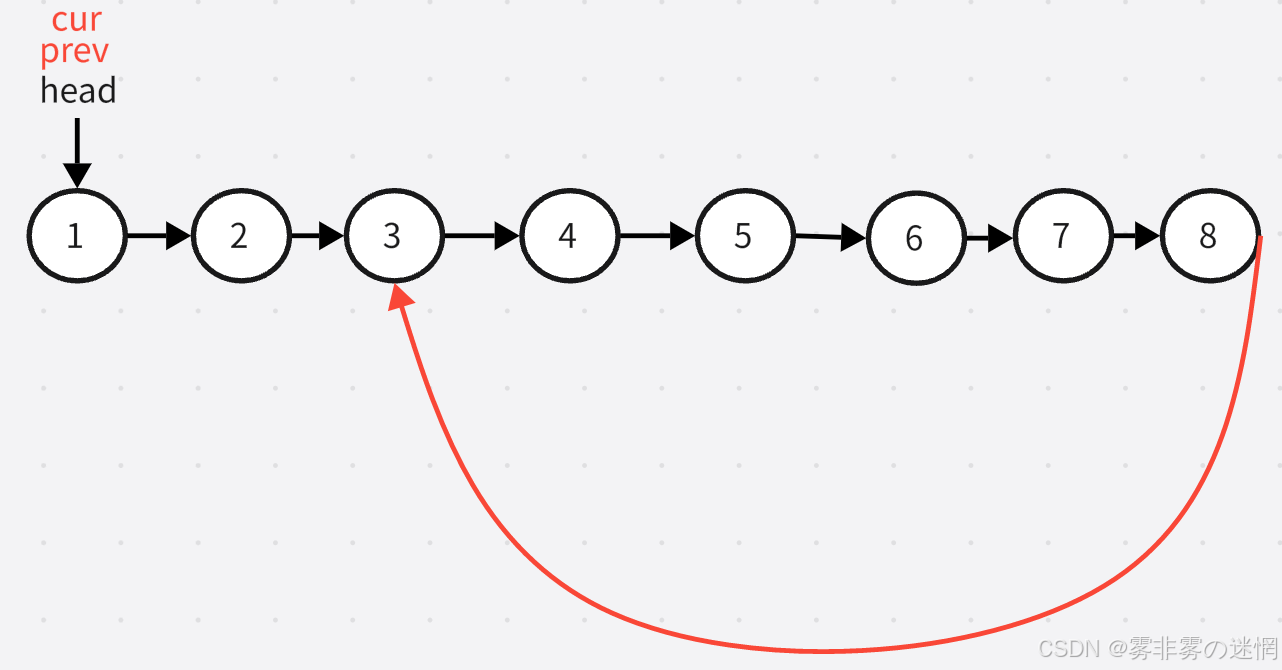
（2）排除以上两种特殊情况之后。我们先设置三个变量（下面小编会分析原因！）

分别是 cur ，刚开始指向空；next 指向 head ->next；pc 指向 head。具体指向如图：

我们通过三个指针的走动来改变链表的指向，例如：

（3）第一轮循环

cpp 复制代码

pc->next = cur;

cur = pc ;
pc = next ;
next = next->next;

在开始时，我们的指针是上面这样的。此时改变pc的指向，pc->next=cur，这时第一个节点就已经翻转过来了，如图：

然后改变三个指针的指向 cur=pc pc=next next=next->next 第一轮循环就走完了

（4）第二轮循环

执行第一条语句 pc->next=cur ，就翻转了第二个节点

然后执行 cur=pc pc=next next=next->next 就改变了三个指针的指向，如下图：

（5）就这样经过几轮循环

cpp 复制代码

while (next != NULL)
{
	pc->next = cur;

	cur = pc ;
	pc = next ;
	next = next->next;
}

next已经指向空，循环停止，前面的链表节点已经完全翻转过来了，如下图：

再将剩余的一个节点翻转过来 pc->next=cur 此时整个链表就翻转过来了

链表OJ（2）

**分析题目：**这题是找到链表的中间节点，因此最简单的方式就是通过遍历链表，记录链表的长度，最后通过除法确立链表的中间节点，再次遍历返回节点（此题并不难，暴力解法也是算法哦！）

思维讲解：

我们可以先来遍历链表，记录链表的长度。需要注意空链表的情况

cpp 复制代码

//如果链表为空
if (head == NULL)
{
	return NULL;
}

//遍历链表、记录长度
int count = 0;
struct ListNode* cur = head;

while (cur != NULL)
{
	count++;
	cur = cur->next;
}

然后通过节点计算中间节点

cpp 复制代码

//计算中间节点
count = count / 2 + 1;

再次遍历节点，通过 count 的减减来返回节点

cpp 复制代码

//再次找中间节点，并返回
cur = head;
while (cur != NULL)
{
	count--;
	if (count == 0)
	{
		break;
	}
	cur = cur->next;
}
return cur;

链表OJ（3）

题目分析：

（1）此题是合并两个有序的链表，方法与"合并两个数组"有异曲同工之妙，但是这里不用创建新的链表，因为题目已经形成了两个链表，我们只需要创建一个头指针改变链表节点的指向就行了

例如：将 List2 剩余的节点移给 pphead ，并不用去创建新的链表

（2）初始化时我们设置2个指针分别是 pphead cur，用来组成新的链表，开始时二者都为空

（3）如果存在某个链表是空，或者都为空。那么就直接返回，这是两种特殊情况

cpp 复制代码

 if(list1==NULL)
    {
        return list2;
    }
    if(list2==NULL)
    {
        return list1;
    }

（4）现在我们通过找两个链表的较小值，来选取节点进行重新组合。因为开始pphead cur 是空，所以需要先处理这种情况，第一次循环找到的较小值应该更新pphead cur，例如：

cpp 复制代码

 if(pphead==NULL)
     {
         pphead = list1;
         cur=pphead;
     }

（5）随后根据找较小值，进行组合就行了，记得更新对应的指针。直到二者有一个为空就结束

cpp 复制代码

 while(list1 != NULL && list2 != NULL)
    {
        //如果list1的当前节点小
        if(list1->val <= list2->val)
        {
            if(pphead==NULL)
            {
                pphead = list1;
                cur=pphead;
            }
            else
            {
                cur->next=list1;
                cur=cur->next;
            }
            list1=list1->next;
        }
        //如果list2的当前节点小
        else
        {
           if(pphead==NULL)
           {
            pphead=list2;
            cur=pphead;
           }
           else
           {
            cur->next=list2;
            cur=cur->next;
           }
           list2=list2->next;
        }
    }

（6）此时可能有某个链表的节点未排完且链表是有序的，根据判断语句，连接到 cur 指针的后面

cpp 复制代码

 //对剩余的链表元素进行连接
    if(list1 == NULL)
    {
        cur->next=list2;
    }
    if(list2==NULL)
    {
        cur->next=list1;
    }

链表OJ（4）

题目分析：

此题是通过判断这个链表是否有循环部分来返回不同的值，我们不能通过遍历去做这题，不然效率特别低，甚至做不出来，这里小编直接告诉大家一种算法：双指针（快慢指针），咱们先按照这个思路来直接解题，先不考虑如何优化！**但是此题真正需要了解的是后面的证明，因为很多面试题是问如何证明二者是否相遇（证明在最后哦！）**小编先来讲如何实现，再来解决推理证明问题！

思维分析：

快慢指针是通过两个指针的移动速度不同，来判断二者是否相遇返回不同的值

例如：现在有两个指针cur 和prev ，prev 的速度是cur 的两倍。如果链表有环，那么当prev 进入环内，cur也会因为与prev的速度不同被prev追赶，二者终会相遇 ，此时链表有环；如果链表没有环，那么prev就会走到空（NULL），得出链表没有环。下面是图示，已助理解！

（1）如果链表为空，直接返回false ；

否则设置两个结构体指针 prev 与cur ，prev 的移动速度是cur的两倍

（2）循环的条件应该是prev 不为空，否则直接返回false。那么如何实现快慢呢？

最简单的方法就是通过次数，比如prev 动一次就记录一次，动了两次就轮到cur走一次，然后重新记录次数。大家可以看下面的代码来理解，小编已经全部注释了！

cpp 复制代码

int count=0;
while(prev)
    {
        //如果prev动了两次，就轮到cur走了
        if(count==2)
        {
            cur=cur->next;
            //如果cur动的时候遇到了prev，就直接返回true
            if(cur==prev)
            {
                return true;
            }
            //重新记录prev动的次数
            count=0;
        }
        else
        {
            //prev动一次，就记录一次
            count++;
            prev=prev->next;
            //如果prev遇到了cur，直接返回true
            if(prev==cur)
            {
                return true;
            }
        }
    }
return false;

代码优化：

直接控制指针的next 来实现走动次数，减少了冗杂的条件判断（下面主要是优化了循环部分）

cpp 复制代码

bool hasCycle(struct ListNode *head) 
{
    //如果链表为空
    if(head==NULL)
    {
        return false;
    }
    //设置两个链表指针
    struct ListNode* prev=head;
    struct ListNode* cur=head;

    while(prev && prev->next)      //     优化
    {
        //cur每次走一步，prev每次走两步
        cur=cur->next;
        prev=prev->next->next;
        //如果相遇
        if(prev==cur)
        {
            return true;
        }
    }
    return false;
}

证明推理：

问：既然一个走一步，一个走两步可以相遇；那么一个走一步，一个走三步呢？以此类推，请证明

首先一个走一步，一个走二步，即二者只差一个单位是一定可以追上的，推理如下：

假如当 cur 进入循环，prev 此时也在循环内，二者相差 N ，如图：

此时 prev 走两步，cur 走一步，二者相差 N-1 ；prev 再走两步， cur 再走一步，二者相差 N-2，那么推下去，N一定会等于 0，也就是二者一定相遇

如果一个走一步，一个走三步呢？是可能永远追不上的，推理如下：

还是当 cur 进入循环，prev 与 cur 相差 N

此时 prev 走三步，cur 走一步，二者相差 N-2 ；prev 再走三步，cur再走一步，相差 N-4；继续推下去，如果 N 是偶数，那么会相遇距离为 0 ；如果 N 是奇数，二者最终会是 -1 ，即 prev 超过了cur ，为下面这个场景：

此时二者相距 C-1（C为圆周长）。prev 再走三步，cur 再走一步，二者相距 3，推理下去，当二者相距 N ，随着二者之间永远相差 2 个单位，就一直无法相遇。其它情况同理类推即可

链表OJ（5）

题目分析：

此题是找到环形链表入环的第一个节点，此题同上题一样，在很多面试题中重点要求证明推理，因此小编会先讲如何证明，当我们知道这个推理过程之后，写起来会很轻松，否则实现真的很难！

证明推理：

我们假设进入环之前的距离为 L ，它们在环的 end 位置相遇，其它变量如图所示：

cur 从起点走到相遇位置用的距离：L + X

prev 从起点到相遇位置用的距离：L + X + C

但是 prev 走的比cur 快，不可能在第一圈内就与 cur 相遇，肯定是在第一圈之后才追赶到的 cur ，具体的圈数我们是无法确定的，因为这个环可大可小，比如：

所以 prev 正确走的距离应该是：L + X + N * C（N为未知数，表示几倍的关系）

那么 cur 与prev 走的路程关系为：2（ L+X）= L + X + N * C（因为prev 的速度是cur的两倍）

所以我们得到：L + X = N * C

L + X = （ N - 1 ）* C + C

最终我们将整倍的圆周路程不看，可以得到：L + X = C

也就是： C - X = L （即下面两段红线长度相等）

那么入环点不就是从 相遇位置与从起点开始运动相遇的位置吗？因此我们来实现代码：

（1）先找prev 与 cur 二者相遇的位置（2）设置一个指针pc 指向head ，返回cur 与pc相遇点

cpp 复制代码

struct ListNode *detectCycle(struct ListNode *head) 
{
    //判断空链表
    if(head==NULL)
    {
        return NULL;
    }
    //设置双指针找相遇位置
    struct ListNode* prev=head;
    struct ListNode*cur=head;

    struct ListNode* pc=head;

    while(prev && prev->next)
    {
        //prev每次走两步
        prev=prev->next->next;
        //cur每次走一步
        cur=cur->next;
        //找相遇位置
        if(cur==prev)
        {
            //pc指针从开头开始走，cur指针从相遇位置开始走，二者相遇既是环的起点
            while(pc != cur)
            {
                cur=cur->next;
                pc=pc->next;
            }
            //此时二者相遇,返回环的起始位置
            return cur;
        }
    }
    return NULL;
}

好了伙伴们，链表OJ题就到这里结束了！大家千万要弄懂最后两题的证明推理啊！可以关注收藏起来！希望大家面试的时候刚好遇到了今天小编整理的最后两题，直接写答案！