【实验性质】
综合性实验。
【实验目的】
掌握迭代法求解线性方程组。
【实验内容】
应用雅可比迭代法和Gauss-Sediel迭代法求解下方程组:

【理论基础】
线性方程组的数值解法分直接算法和迭代算法。迭代法将方程组的求解转化为构造一个向量序列,如果该向量序列存在极限,其极限就是方程组的解。
迭代法程序简单,但有时工作量较大,在有限步内,得不到精确解,适宜系数矩阵阶数较高的问题。
构造关于解向量的迭代序列 ,的常见方法有Jacobi迭代和Gauss-Seidel加速迭代。
,的常见方法有Jacobi迭代和Gauss-Seidel加速迭代。
设:
统一的迭代公式为:
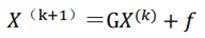 −1
−1
对于雅可比迭代,矩阵 ;对于高斯-赛德尔迭代,G = −(𝐷+L) 𝑈,f =(𝐷+L)−1𝑏。
;对于高斯-赛德尔迭代,G = −(𝐷+L) 𝑈,f =(𝐷+L)−1𝑏。
实际的计算与编程应尽量避免矩阵求逆、矩阵相乘等运算,而使用如下公式:

【实验过程】
取三个不同初值,分别用雅可比法和高斯-塞得尔法求解,用表格记载求解过程,并分析迭代初值、迭代公式对迭代的影响。
附表:
|---|----|-----|------|-----|------|
| || 雅可比法 || 高斯-塞得尔法 ||
| | 初值 | 近似根 | 迭代次数 | 近似根 | 迭代次数 |
| 1 | | | | | |
| 2 | | | | | |
| 3 | | | | | |
代码:
主函数:
//实验四
#include <iostream>
#include <windows.h>
#include "colvector.h"
#include "matrix.h"
#include <windows.h>
#include "linearequations.h"
using namespace std;
int main()
{
double a1[]={8,7,0,0,6,12,5,0,0,4,9,3,0,0,1,2};
double b1[]={0,-2,8,6};
double x1[]={0,0,0,0};
double e=0.0001;
int flag=1,max=100;
Matrix A(4,4);
ColVector b(4),x(4),x0(4);
A.initMatrix(a1);
b.initMatrix(b1);
x0.initMatrix(x1);
LinearEquations obj;
obj.JacobiIterativeMethod(A,b,e,x0,max,flag,x);
cout<<x<<endl;
return 0;
}
头文件:
#ifndef LINEAREQUATIONS_H#define LINEAREQUATIONS_H#include "matrix.h"#include "colvector.h"#include <math.h>class LinearEquations{public: void GaussElimin(Matrix A,ColVector b,int &flag,ColVector &x); void colPivotGaussElimin(Matrix A,ColVector b,int &flag,ColVector &x); void LUDecomposition(Matrix &mat,int &flag,Matrix &L,Matrix &U,int type=1); void TrigDecompositionMethod(Matrix &A,ColVector &b,int &flag,ColVector &x,int type=1); void Catchup(ColVector&a,ColVector &b,ColVector &c,ColVector &f,int &flag,ColVector &x,int type=1); LinearEquations(); //雅可比迭代 void JacobiIterativeMethod(Matrix &A,ColVector &b,double e,ColVector &x0,int MAX, int &flag,ColVector &x); //高斯-赛德尔迭代 void Gauss_SeidelIterativeMethod(Matrix &A,ColVector &b,double e,ColVector &x0,int MAX, int &flag,ColVector &x);};#endif // LINEAREQUATIONS_H源文件:
#include "linearequations.h"
LinearEquations::LinearEquations()
{
}
void LinearEquations::GaussElimin(Matrix A,ColVector b,int &flag,ColVector &x)
{
flag=1;
int n=A.getRowSize();
if(n!=A.getColSize() || n!=b.getRowSize())
{
flag =0;
return;
}
cout<<"初始曾广矩阵"<<Matrix::merge(A,b)<<endl;
for(int k=1;k<=n-1;k++)
{
for(int i=k+1;i<=n;i++)
{
if(A(k,k)==0)
{
flag =0;
return;
}
double m=A(i,k)/A(k,k);
for(int j=1;j<=n;j++)
{
A(i,j)=A(i,j)-m*A(k,j);
}
b[i]=b[i]-m*b[k];
}
cout<<"第"<<k<<"次消元"<<Matrix::merge(A,b)<<endl;
}
cout<<"解 x"<<endl;
x=ColVector(n);
if(A(n,n)==0)
{
flag=0;
return;
}
x[n]=b[n]/A(n,n);
cout<<x<<endl;
for(int i=n-1;i>=1;i--)
{
double sum=0;
for(int j=i+1;j<=n;j++)
{
sum+=A(i,j)*x[j];
}
x[i]=(b[i]-sum)/A(i,i);
cout<<"解 x"<<endl;
cout<<x<<endl;
}
}
void LinearEquations::colPivotGaussElimin(Matrix A,ColVector b,int &flag,ColVector &x)
{
flag=1;
int n=A.getRowSize();
if(n!=A.getColSize() || n!=b.getRowSize())
{
flag =0;
return;
}
cout<<"初始曾广矩阵"<<Matrix::merge(A,b)<<endl;
for(int k=1;k<=n-1;k++)
{
double max=fabs(A(k,k));
int p=k;
for(int w=k+1;w<=n;w++)
{
if(max< fabs(A(w,k))){
max=fabs(A(w,k));
p=w;
}
}
if(max==0){
flag=0;
return;
}
if(p!=k){
double temp=0;
for(int s=1;s<=n;s++)
{
temp =A(k,s);
A(k,s)=A(p,s);
A(p,s)=temp;
}
temp=b[k];
b[k]=b[p];
b[p]=temp;
}
for(int i=k+1;i<=n;i++)
{
if(A(k,k)==0)
{
flag =0;
return;
}
double m=A(i,k)/A(k,k);
for(int j=1;j<=n;j++)
{
A(i,j)=A(i,j)-m*A(k,j);
}
b[i]=b[i]-m*b[k];
}
cout<<"第"<<k<<"次消元"<<Matrix::merge(A,b)<<endl;
}
cout<<"解 x"<<endl;
x=ColVector(n);
if(A(n,n)==0)
{
flag=0;
return;
}
x[n]=b[n]/A(n,n);
cout<<x<<endl;
for(int i=n-1;i>=1;i--)
{
double sum=0;
for(int j=i+1;j<=n;j++)
{
sum+=A(i,j)*x[j];
}
x[i]=(b[i]-sum)/A(i,i);
cout<<"解 x"<<endl;
cout<<x<<endl;
}
}
void LinearEquations::LUDecomposition(Matrix &mat,int &flag,Matrix &L,Matrix &U,int type)
{
flag=0;
int n=mat.getRowSize();
if(n!=mat.getColSize()||type<1||type>2){
flag=-1;
return;
}
L=Matrix(n,n);
U=Matrix(n,n);
switch(type){
case 1:
for(int i=1;i<+n;i++){
U(1,i)=mat(1,i);
}
for(int i=1;i<=n;i++){
L(i,1)=mat(i,1)/U(1,1);
}
for(int k=2;k<=n;k++)
{
for(int j=k;j<=n;j++){
double sum=0;
for(int r=1;r<=k-1;r++){
sum+=L(k,r)*U(r,j);
}
U(k,j)=mat(k,j)-sum;
}
for(int i=k;i<=n;i++){
double sum=0;
for(int r=1;r<=k-1;r++){
sum+=L(i,r)*U(r,k);
}
L(i,k)=(mat(i,k)-sum)/U(k,k);
}
}
break;
case 2:
for(int k=1;k<=n;k++)
{
for(int j=k;j<=n;j++)
{
double sum=0;
if(k>1){
for(int r=1;r<=k-1;r++){
sum+=L(j,r)*U(r,k);
}
}
L(j,k)=mat(j,k)-sum;
}
for(int j=k;j<=n;j++)
{
if(L(k,k)==0){
flag=0;
return ;
}
double sum=0;
if(k>1)
{
for(int r=1;r<=k-1;r++){
sum+=L(k,r)+U(r,j);
}
}
U(k,j)=(mat(k,j)-sum)/L(k,k);
}
}
break;
}
}
void LinearEquations::TrigDecompositionMethod(Matrix &A,ColVector &b,int &flag,ColVector &x,int type)
{
flag =1;
int n=A.getRowSize();
if(n!=A.getColSize()||n!=b.getRowSize()||type<1||type>2)
{
flag=0;
return;
}
Matrix L,U;
ColVector y(n);
x=ColVector(n);
switch(type){
case 1:
LUDecomposition(A,flag,L,U);
if(flag== -1)
{
return;
}
y[1]=b[1];
for(int i=2;i<=n;i++)
{
double sum=0;
for(int k=1;k<=i-1;k++)
{
sum+=L(i,k)*y[k];
}
y[i]=b[i]-sum;
}
cout<<"y="<<y<<endl;
if(U(n,n)==0)
{
flag=0;
return;
}
x[n]=y[n]/U(n,n);
for(int i=n-1;i>=1;i--)
{
if(U(i,i)==0){
flag=0;
return;
}
double sum=0;
for(int k=i+1;k<=n;k++)
{
sum+=U(i,k)*x[k];
}
x[i]=(y[i]-sum)/U(i,i);
}
break;
case 2:
LUDecomposition(A,flag,L,U);
if(flag<1)
{
return;
}
if(L(1,1)==0)
{
flag=0;
return;
}
y[1]=b[1]/L(1,1);
for(int i=2;i<=n;i++)
{
if(L(i,i)<=0){
flag=0;
return;
}
double sum=0;
for(int k=1;k<=i-1;k++)
{
sum+=L(i,k)*y[k];
}
y[i]=(b[i]-sum)/L(i,i);
}
x[n]=y[n];
for(int i=n-1;i>=1;i--)
{
double sum=0;
for(int k=i+1;k<=n;k++)
{
sum+=U(i,k)*x[k];
}
x[i]=y[i]-sum;
}
break;
}
}
void LinearEquations::Catchup(ColVector&a,ColVector &b,ColVector &c,ColVector &f,int &flag,ColVector &x,int type)
{
flag=1;
int n=b.getRowSize();
if(n!=a.getRowSize()||n!=b.getRowSize()||n!=f.getRowSize())
{
flag=0;
return;
}
if(fabs(b[1])<=fabs(c[1])||fabs(b[n])<=fabs(a[n])||b[1]*c[1]==0||a[n]*b[n]==0)
{
flag=0;
return;
}
for(int i=2;i<=n-1;i++)
if(fabs(b[i])<fabs(a[i])+fabs(c[i])||a[i]*c[i]==0)
{
flag=0;
return;
}
ColVector d(n),u(n),y(n),l(n);
x=ColVector (n);
switch(type){
case 1:
d=c;
u[1]=b[1];
for(int i=2;i<=n;i++)
{
l[i]=a[i]/u[i-1];
u[i]=b[i]-l[i]*c[i-1];
}
y[1]=f[1];
for(int i=2;i<=n;i++)
{
y[i]=f[i]-l[i]*y[i-1];
}
x[n]=y[n]/u[n];
for(int i=n-1;i>=1;i--)
{
x[i]=(y[i]-c[i]*x[i+1])/u[i];
}
break;
case 2:
l[1]=b[1];
for(int i=1;i<=n-1;i++)
{
u[i]=c[i]/l[i];
l[i+1]=b[i+1]-a[i+1]*u[i];
}
y[1]=f[1]/l[1];
for(int i=2;i<=n;i++)
{
y[i]=(f[i]-a[i]*y[i-1])/l[i];
}
x[n]=y[n];
for(int i=n-1;i>=1;i--)
{
x[i]=y[i]-u[i]*x[i+1];
}
break;
}
}
void LinearEquations::JacobiIterativeMethod(Matrix &A,ColVector &b,
double e,ColVector &x0,int MAX, int &flag,ColVector &x){
flag =1;
int n=A.getRowSize();
if(n!=b.getRowSize()||n!=A.getColSize()||n!=x0.getRowSize())
{
flag=0;
return;
}
for(int i=1;i<=n;i++){
if(A(i,i)==0){
flag=0;
return ;
}
}
double eps=0;
int k=0;
int sum=0;
int i,j;
ColVector x1(n);
ColVector dist(n);
while(k<MAX){
for(i=1;i<=n;i++){
double sum=0;
for(j=1;j<=n;j++){
if(j==1){
continue;
}
sum+=A(i,j)*x0[j];
}
x1[i]=(b[i]-sum)/A(i,i);
}
k++;
dist=x1-x0;
eps=dist.norm(3);
cout<<endl;
cout<<"k="<<k<<"\nx1="<<x1<<"x0="<<x0<<endl;
cout<<"dist="<<dist<<endl;
cout<<"eps="<<eps<<endl;
if(eps<=e){
break;
}
else{
x0=x1;
}
}
if(k==MAX){
flag=0;
return;
}
else{
x=x1;
}
}
void LinearEquations::Gauss_SeidelIterativeMethod(Matrix &A,ColVector &b,double e,
ColVector &x0,int MAX, int &flag,ColVector &x){
flag =1;
int n=A.getRowSize();
if(n!=b.getRowSize()||n!=A.getColSize()||n!=x0.getRowSize())
{
flag=0;
return;
}
for(int i=1;i<=n;i++){
if(A(i,i)==0){
flag=0;
return ;
}
}
double eps=0;
int k=0;
ColVector x1(n);
ColVector dist(n);
while(k<MAX){
for(int i=1;i<=n;i++){
double sum=0;
for(int j=1;j<=n;j++){
if(j<i){
sum+=A(i,j)*x1[j];
}
else if(j==i){
continue;
}
else{
sum+=A(i,j)*x0[j];
}
}
x1[i]=(b[i]-sum)/A(i,i);
}
k++;
dist=x1-x0;
eps=dist.norm(3);
cout<<"k="<<k<<"\nx1="<<x1<<"x0="<<x0<<endl;
cout<<"dist="<<dist<<endl;
cout<<"eps="<<eps<<endl;
if(eps<=e){
break;
}
else{
x0=x1;
}
}
if(k==MAX){
flag=0;
return;
}
else{
x=x1;
}
}
运行结果:

【实验心得】
我在实验中使用了间接方法解线性方程组,获得了一些心得。首先,我发现使用间接方法可以简化计算过程,特别适用于方程组较大的情况。通过将方程组转化为矩阵形式,并利用矩阵的运算性质来求解,可以大大减少计算量。其次,我注意到间接方法的精度较高,能够得到比较准确的解。与直接方法相比,间接方法不容易出现舍入误差,因为矩阵运算过程中的舍入误差可以通过精确的结果进行修正。此外,我发现间接方法还可以应用于其他数学问题的求解中,例如线性最小二乘问题等。总体来说,间接方法是一种简单高效、精度较高的解线性方程组的方法,对于数学问题的求解也具有一定的推广价值。通过这次实验,我不仅学到了解线性方程组的间接方法,还深入了解了矩阵运算的原理和应用,对数学问题的求解能力也有了一定的提升。
得 分________
评阅日期________
教师签名________