课程10. 聚类问题
- 聚类
- 此类表述的难点
- [K 均值法](#K 均值法)
- 结论
-
- [在 sklearn 中的实现](#在 sklearn 中的实现)
- 如何处理已发现的问题?
- 示例
- DBSCAN
-
- [DBSCAN 算法](#DBSCAN 算法)
聚类
上一讲我们开始学习无监督学习问题,并讨论了降维问题。今天我们将继续学习无监督学习问题,并讨论聚类问题。
什么是聚类?
聚类是将原始未标记数据集划分为几组,这些组称为聚类。聚类是一个相当宽泛的概念。以下陈述可以被视为聚类的一个显著特征:
"聚类中对象之间的平均距离明显小于一对对象之间的平均距离,其中一个对象属于该聚类,另一个不属于该聚类。"
让我们正式地表述这个问题。
已知:
设 X X X 为我们从中收集训练样本的对象空间。
X N X^N XN = { x i } i = 1 N \{x^i\}_{i=1}^N {xi}i=1N 为训练样本。让我们再次注意样本中没有 y y y 个标签。
ρ : X × X → [ 0 , ∞ ) \rho: X × X → [0,∞) ρ:X×X→[0,∞) 是对象之间的距离函数。
注意,与度量算法一样,距离函数反映了我们对"对象接近度"概念的期望。
求:
y i ∈ Y y_i \in Y yi∈Y 是对象所属聚类的标签。对它们的要求:
- 每个聚类由距离较近的对象组成。
- 不同聚类中的对象彼此相距较远。

此类表述的难点
这种聚类问题的表述有些模糊。根据 Hadamard 理论,存在一个关于该问题表述正确性的概念。
根据 Hadamard 理论,如果满足以下条件,则该问题表述正确:
- 该问题的解存在
- 该问题的解是唯一的
- 该问题的解持续依赖于初始数据(即,如果我们稍微更改初始数据,解不会发生太大变化)。
显然,从这个定义的角度来看,聚类问题的表述是错误的。
1) 存在(非平凡)解
在解决聚类问题时,我们经常处理高维数据,这些数据我们无法通过视觉或其他任何概览方式进行分析。这正是我们想要解决这个问题的原因------通过求解该问题,我们可以获得对现有数据的一些建设性描述。在开始解决问题时,我们对我们想要识别的聚类结构的存在做出了一个重要的假设。
但没有人向我们保证聚类结构的存在。很有可能,现有数据是从单一分布中采样的,根本没有真正划分成聚类。在这种情况下,发现的聚类结构要么微不足道,要么无法反映数据的真实结构。
2) 解的唯一性
当数据中某些聚类结构客观存在时,它可能具有模糊性。我们举个例子。

所有这些让我们意识到,我们面临的任务并不容易,主要是因为它的模糊性。然而,有一些相当有效的方法可以解决这个问题。我们将会了解这些方法。
K 均值法
最流行的聚类方法之一称为K 均值 。它被广泛用于解决聚类问题。K 均值算法 是更通用的EM 算法的一个特例。
我们首先来了解一下 K 均值算法,然后再看看它如何推广到 EM 算法。为了讨论该算法,我们先来介绍一下聚类中心的概念。
聚类中心是表示分配给聚类的区域的质心的一个点。简而言之,它是该聚类的几何中点。如果我们知道一组属于某个聚类的点,那么确定它的中心就非常简单:我们只需计算每个坐标上所有点的平均值即可。这组坐标将为我们提供一个聚类中心的估计值。
那么,k-means 算法 是什么样的呢?
我们假设现有数据集中的聚类数量预先已知,等于 K K K。
需要注意的是,所需的聚类可以唯一地定义为特征空间中的 K K K 个点。
假设所需聚类中心的初始近似值为 Θ 0 = ( θ 1 0 . . . θ k 0 ) \Theta_0 = (\theta_1^0 ... \theta_k^0) Θ0=(θ10...θk0)
直到收敛:
- 给定当前近似值 G i G_i Gi,计算现有数据集中的点属于哪些聚类:对于数据集中的所有 x j x_j xj, g j i : = arg min p = 1... k ( ρ ( Θ p i − 1 , x j ) ) g_j^i := \arg\min\limits_{p = 1 ... k}(\rho(Θ_p^{i-1}, x_j)) gji:=argp=1...kmin(ρ(Θpi−1,xj))。
- 根据计算出的数据集按聚类分布 G = ( g 1 i . . . g N i ) g_1^i ... g_N^i) g1i...gNi),我们重新计算新的聚类中心 Θ i = ( θ 1 i . . . θ k i ) \Theta_i = (\theta_1^i ... \theta_k^i) Θi=(θ1i...θki)。
注意 :提前说明收敛的含义非常重要。我们将收敛理解为这样一种情况:后续每一步都只会导致聚类中心估计值发生极其微小的变化。在下一个例子中,我们将看到从某一步开始,这个估计值根本不会改变。实际上,在许多算法中,我们会设置一个较小的数 ϵ ϵ ϵ,然后将估计值的变化与该值进行比较。如果结果显示,估计值在每一步的变化小于 ϵ ϵ ϵ,我们就说达到了收敛。
让我们用一个例子来解释一下该算法的运作。
首先,我们只考虑两个聚类,并在二维情况下(即特征描述向量为二维时)演示该算法的运作。
python
from matplotlib import pyplot as plt
import numpy as np
import seaborn as sns
sns.set_theme()
a_x = 3.5 * np.random.randn(50) + 7
a_y = 3.5 * np.random.randn(50) + 7
b_x = 3.5 * np.random.randn(50) - 7
b_y = 3.5 * np.random.randn(50) - 7
plt.figure(figsize=(12, 12))
plt.scatter(a_x, a_y)
plt.scatter(b_x, b_y)输出:

python
import numpy as np
import matplotlib.pyplot as plt
# 定义距离函数
dist = lambda x1, y1, x2, y2: np.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)
# 定义"点"类
class point:
def __init__(self, x, y):
self.x = x
self.y = y
# 计算当前点与另一个点之间的距离
def count_distance(self, p):
return dist(self.x, self.y, p.x, p.y)
# 设置点所属的聚类
def set_cluster(self, cluster):
self.cluster = cluster
# 绘制点
def draw(self, color):
plt.scatter([self.x], [self.y], c=color)
# 将所有点合并到一个列表中,不填充对象标签信息
points = [point(a_x[i], a_y[i]) for i in range(len(a_x))] + [
point(b_x[i], b_y[i]) for i in range(len(b_x))
]
# 创建一个大小为 12x12 的图形
plt.figure(figsize=(12, 12))
# 绘制所有点,颜色为黑色
for i in range(len(points)):
points[i].draw("black")输出:

python
# 让我们写一个单步函数
def step(points, cluster_center_1, cluster_center_2):
for i in range(len(points)):
distance_1 = points[i].count_distance(cluster_center_1)
distance_2 = points[i].count_distance(cluster_center_2)
if distance_1 < distance_2:
points[i].set_cluster(1)
else:
points[i].set_cluster(2)
return points
python
# 聚类中心重新计算函数
def find_centers(points):
cl1 = []
cl2 = []
for i in range(len(points)):
if points[i].cluster == 1:
cl1.append(points[i])
else:
cl2.append(points[i])
cluster_center_1 = point(np.mean([p.x for p in cl1]),
np.mean([p.y for p in cl1]))
cluster_center_2 = point(np.mean([p.x for p in cl2]),
np.mean([p.y for p in cl2]))
return cluster_center_1, cluster_center_2
python
# 循环的一次迭代
# 更新函数有两种运行模式:在零模式下,它会根据中心数据重新计算每个聚类的点的新分布;在第一个模式下,它会为指定的聚类重新计算新的中心。
# 这些模式由输入变量 rjm 编码,该变量取两个值之一 - 0 或 1。在输出端,我们将此变量的值更改为相反的值。
def update(points, cluster_center_1, cluster_center_2, rjm):
if rjm:
c1 = cluster_center_1
c2 = cluster_center_2
cluster_center_1, cluster_center_2 = find_centers(points)
plt.arrow(c1.x, c1.y, cluster_center_1.x - c1.x, cluster_center_1.y - c1.y, color='black')
plt.arrow(c2.x, c2.y, cluster_center_2.x - c2.x, cluster_center_2.y - c2.y, color='black')
else:
points = step(points, cluster_center_1, cluster_center_2)
for p in points:
p.draw('r' if p.cluster == 1 else 'b')
cluster_center_1.draw('m')
cluster_center_2.draw('y')
return points, cluster_center_1, cluster_center_2, 1-rjm此时,一个自然而然的问题出现了------聚类中心的初始近似值是根据什么原则设定的?
一般来说,有一些启发式方法可以帮助使这种选择并非完全随机。但我们不会深入探讨这个问题,而是遵循经典算法,随机选择初始近似值。例如,(-15,10) 和 (15, -10)。
python
c1 = point(-15,10)
c2 = point(15,-10)
rjm = 0
python
"""
更新函数仅生成并绘制了算法的一个步骤!
要观察算法的运行,您需要多次执行此单元格(以及所有包含更新函数的单元格)!
"""
plt.figure(figsize=(10,10))
points, c1, c2, rjm = update(points, c1, c2, rjm)输出:

让我们推广到几个集群的情况
python
import collections
from collections import defaultdict
def step(points, centers):
for i in range(len(points)):
distances = [points[i].count_distance(centers[k]) for k in centers.keys()]
cluster = np.argmin(distances) + 1
points[i].set_cluster(cluster)
return points
def find_centers(points):
clusters = defaultdict(list)
centers = {}
for i in range(len(points)):
clusters[points[i].cluster].append(points[i])
for k in clusters.keys():
centers[k] = point(np.mean([p.x for p in clusters[k]]),
np.mean([p.y for p in clusters[k]]))
return centers
def update(points, centers, rjm, colors_clusters, colors_centers):
if rjm:
c = centers
centers = find_centers(points)
for k in centers.keys():
plt.arrow(c[k].x, c[k].y, centers[k].x - c[k].x, centers[k].y - c[k].y, color='black')
else:
points = step(points, centers)
for p in points:
p.draw(colors_clusters[p.cluster - 1])
for i,k in enumerate(centers.keys()):
centers[k].draw(colors_centers[i])
return points, centers, 1-rjm
python
from matplotlib import pyplot as plt
import numpy as np
a_x = 3.*np.random.randn(50) + 8
a_y = 3.*np.random.randn(50) + 8
b_x = 3.*np.random.randn(50)
b_y = 3.*np.random.randn(50) - 8
c_x = 3.*np.random.randn(50) - 8
c_y = 3.*np.random.randn(50) + 8
plt.figure(figsize=(10,10))
plt.scatter(a_x, a_y)
plt.scatter(b_x, b_y)
plt.scatter(c_x, c_y)输出:

python
points = (
[point(a_x[i], a_y[i]) for i in range(len(a_x))]
+ [point(b_x[i], b_y[i]) for i in range(len(b_x))]
+ [point(c_x[i], c_y[i]) for i in range(len(c_x))]
)
plt.figure(figsize=(10, 10))
for i in range(len(points)):
points[i].draw("black")输出:
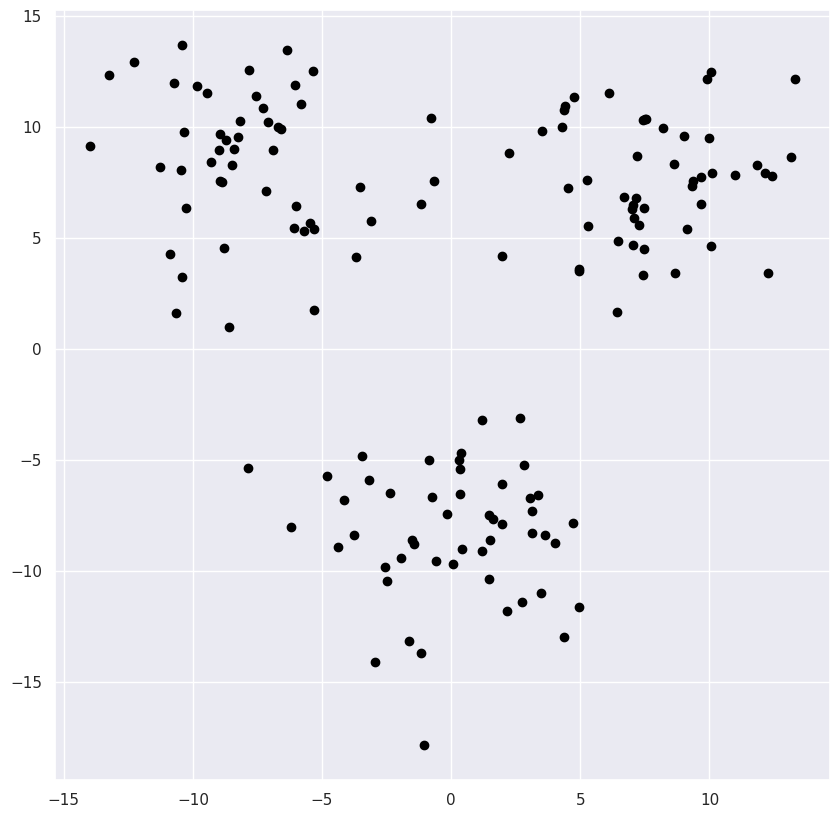
python
centers = {1: point(-15,-15),2: point(15,-15),3: point(0,15)}
colors_clusters = ['g', 'b', 'r']
colors_centers = ['y', 'm', '#000000']
rjm = 0
plt.figure(figsize=(10,10))
points, centers, rjm = update(points, centers, rjm, colors_clusters, colors_centers)输出:

如果我们选择其他起始近似值会怎样?
python
centers = {1: point(-1, 20),2: point(15,5),3: point(-15,-15)}
colors_clusters = ['g', 'b', 'r']
colors_centers = ['y', 'm', '#000000']
rjm = 0
plt.figure(figsize=(10,10))
points, centers, rjm = update(points, centers, rjm, colors_clusters, colors_centers)输出:

如果我们选择了错误的聚类数量会怎么样?
python
# 2 个集群
centers = {1: point(-1, 20),2: point(15,5)}
colors_clusters = ['g', 'b']
colors_centers = ['y', 'm']
rjm = 0
python
plt.figure(figsize=(10,10))
points, centers, rjm = update(points, centers, rjm, colors_clusters, colors_centers)输出:

python
# 4个集群
centers = {1: point(-1, 20),2: point(15,5), 3: point(-10, -10), 4: point(10,10)}
colors_clusters = ['g', 'b', 'r', '#ff8243']
colors_centers = ['y', 'm', '#000000', "#8b00ff"]
rjm = 0
python
plt.figure(figsize=(10,10))
points, centers, rjm = update(points, centers, rjm, colors_clusters, colors_centers)输出:

结论
- 该算法高度依赖于聚类中心的初始近似值。
- 如果聚类数量指定错误,我们得到的形式正确的结果可能无法完全反映实际情况。
在 sklearn 中的实现
python
from sklearn.cluster import KMeans
python
X = [[p.x, p.y] for p in points]
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
python
kmeans.labels_输出:

python
plt.figure(figsize=(10,10))
for i,p in enumerate(X):
plt.scatter([p[0]], [p[1]], c=colors_clusters[kmeans.labels_[i]])输出:

python
kmeans.inertia_输出:2500.5010444312366
如果我们设置不同数量的集群会怎么样?
python
inertias = []
for i in range(1, 26):
kmeans = KMeans(n_clusters=i,random_state=0).fit(X)
inertias.append(kmeans.inertia_)
python
plt.figure(figsize=(15, 7))
plt.title('Dependence of inertia on the number of clusters')
plt.plot(np.arange(1, 26, 1), inertias)输出:

python
kmeans = KMeans(n_clusters=4,random_state=0).fit(X)
python
plt.figure(figsize=(10,10))
colors_clusters = ['g', 'b', 'r', '#ff8243']
for i,p in enumerate(X):
plt.scatter([p[0]], [p[1]], c=colors_clusters[kmeans.labels_[i]])输出:

python
plt.figure(figsize=(10,10))
kmeans = KMeans(n_clusters=5,random_state=0).fit(X)
colors_clusters = ['g', 'b', 'r', '#ff8243', "#8b00ff"]
for i,p in enumerate(X):
plt.scatter([p[0]], [p[1]], c=colors_clusters[kmeans.labels_[i]])输出:

补充知识点:EM 算法
EM 算法(期望最大化)是一种在给定一组观测变量 x x x 的情况下,通过引入一些隐藏变量 G G G(即我们无法直接观测,但可以以某种方式估计的变量)的向量来估计模型 Θ Θ Θ 的最优参数的算法。
让我们将其与 k-means 算法进行类比:最优参数 Θ Θ Θ 定义了点在聚类中的分布。它们是期望的聚类标签。隐藏变量 G G G 定义了聚类中心。我们无法直接观测它们,但可以用当前的近似值 Θ Θ Θ 来估计它们。观测变量是数据集中点的坐标。
EM 算法与 K 均值算法类似,包含两个迭代重复的步骤:
0.设置参数 Θ 0 Θ_0 Θ0 的初始近似值
直至收敛:
- 期望步骤:给定当前近似值 Θ i − 1 Θ_{i-1} Θi−1,计算隐藏变量 G i G_i Gi 的期望值
- 最大化步骤:求解给定隐藏变量 G i G_i Gi 时,最大化观测值 x x x 的似然值问题。即 Θ i = a r g m a x ( P ( x ∣ G i , Θ ) ) Θ_i = argmax(P(x|G_i, Θ)) Θi=argmax(P(x∣Gi,Θ))
当参数向量 Θ Θ Θ 的变化在某一步骤变得不显著时,算法将停止工作。
注意:需要注意的是,K-Means 只能检测相当简单的聚类结构。例如,它在检测环状聚类时会遇到问题,这时需要使用其他聚类方法。
如何处理已发现的问题?
-
多启动。我们可以使用不同的聚类中心初始近似值多次运行该算法,然后选择每个对象到其聚类质心的距离总和最小的解。
-
层次聚类
层次聚类
层次聚类包含两种不同的全局方法------凝聚层次聚类和划分层次聚类。它们之间的区别在于,凝聚聚类涉及不同聚类的顺序合并,而划分聚类涉及顺序划分。在本讲座中,我们将讨论凝聚聚类。
层次聚类的思想是持续执行某种迭代过程(即由多个重复步骤组成的过程),该过程允许基于已知的 N N N 个聚类划分,合并其中最近的一个(或者,相反,将其中一个聚类拆分成两个不同的聚类),从而将样本划分为 N − 1 N-1 N−1 个聚类(或 N + 1 N+1 N+1 个)。因此,我们将获得一系列划分成不同数量聚类的样本,并从中选择最佳的聚类。
Lance-Williams 算法
该算法允许我们执行聚类的顺序合并,前提是我们有一个函数可以测量两个聚类之间的距离。我们将此函数称为 R ( U , V ) R(U,V) R(U,V),其中 U U U 和 V V V 是一些聚类。
- 假设所有聚类最初都是单元素聚类。也就是说,在初始近似中,样本中的每个对象都是一个单独的聚类。
- 重复以下步骤 L − 1 L-1 L−1 次,其中 L L L 是样本的大小:
- 根据函数 R ( U , V ) R(U, V) R(U,V) 的值,在我们的结构中找到两个最近的聚类,并将它们合并为一个聚类。我们将在此步骤 t t t 找到的聚类结构表示为 C t C_t Ct。
在该算法的输出中,我们获得了一系列聚类划分序列,分别为 C 1 . . . C L C_1 ... C_L C1...CL。其中, C 1 C_1 C1 划分为多个独立聚类, C 2 C_2 C2 划分为 L − 1 L-1 L−1 个独立聚类和一个包含 2 个点的聚类,以此类推; C L C_L CL 划分为一个包含所有对象的聚类。
为了便于可视化此聚类选项,通常使用一种称为树状图 的特殊图表。

Lance-Williams 公式
如何测量聚类之间的距离?
实际上有很多不同的选择。
例如:
- 最近邻距离。 R ( U , V ) R(U, V) R(U,V) = min x ∈ U , y ∈ V ( ρ ( x , y ) ) \min\limits_{x \in U, y \in V}(\rho(x,y)) x∈U,y∈Vmin(ρ(x,y))
- 远邻距离。 R ( U , V ) R(U, V) R(U,V) = max x ∈ U , y ∈ V ( ρ ( x , y ) ) \max\limits_{x \in U, y \in V}(\rho(x,y)) x∈U,y∈Vmax(ρ(x,y))
- 平均组距离。 R ( U , V ) R(U, V) R(U,V) = 1 N ∑ x ∈ U , y ∈ V ( ρ ( x , y ) ) \frac{1}{N}\sum\limits_{x \in U, y \in V}(\rho(x,y)) N1x∈U,y∈V∑(ρ(x,y))
我们可以基于我们能够形成的启发式方法,结合我们对主题领域的了解或问题的特征,以及通过尝试多个选项并确定哪种聚类能够最小化每个对象到其聚类中心的距离之和,来选择最适合我们任务的选项。
有一个公式可以描述所有这些以及许多其他计算聚类间距离的方法。
我们假设聚类 W W W = U ⋃ V U \bigcup V U⋃V。我们还假设我们知道聚类 R ( U , S ) R(U, S) R(U,S) 和 R ( V , S ) R(V, S) R(V,S) 之间的距离。
那么 R ( W , S ) = α U × R ( U , S ) + α V × R ( V , S ) + β × R ( U , V ) + γ × ∣ R ( U , S ) − R ( V , S ) ∣ R(W, S) = α_U\times R(U,S) + α_V\times R(V,S) + β\times R(U,V) + γ\times |R(U,S) - R(V,S)| R(W,S)=αU×R(U,S)+αV×R(V,S)+β×R(U,V)+γ×∣R(U,S)−R(V,S)∣
在这个公式中,我们可以选择系数 α U , α V , β , γ α_U, α_V, β, γ αU,αV,β,γ
例如,如果我们设定 α U = α V = 1 2 , β = 0 , γ = − 1 2 α_U = α_V = \frac{1}{2}, β=0, γ=-\frac{1}{2} αU=αV=21,β=0,γ=−21,那么我们就得到了最近邻距离的公式。
而通过系数 α U = α V = 1 2 , β = 0 , γ = 1 2 α_U = α_V = \frac{1}{2}, β=0, γ=\frac{1}{2} αU=αV=21,β=0,γ=21,我们就得到了远邻距离。

在Scipy中实现
python
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
plt.figure(figsize=(10,10))
X = np.array([[5,3],
[10,15],
[15,12],
[24,10],
[30,30],
[85,70],
[71,80],
[60,78],
[70,55],
[80,91],])
plt.scatter(X[:,0],X[:,1])输出:

python
linked = linkage(X, 'single')
labelList = [f'point_{i}' for i in range(1, len(X)+1)]
plt.figure(figsize=(10, 7))
dendrogram(linked,
orientation='top',
labels=labelList,
distance_sort='descending',
show_leaf_counts=True)
plt.show()输出:

python
linked输出:

示例
在之前的一节课中,我们学习了课程5,该示例利用线性回归模型解决了根据银行客户收入特征预测其存款规模的问题。
通过此示例,我们证明了,如果我们为构成数据集的每个聚类构建单独的模型,那么使用线性模型是合理的。
让我回顾一下问题陈述:
假设我们想根据某人的收入特征预测其在某家银行的存款规模。这家银行的客户分为几类:退休人员、有子女的家庭、青少年、商人和年轻的机器学习专家。
该数据集可从链接获取。
python
import numpy as np
import pandas as pd
X = pd.read_csv('credit.csv')让我提醒你,这个数据集包含有关客户月收入和银行账户的信息。
python
from matplotlib import pyplot as plt
import seaborn
seaborn.set_theme()
plt.figure(figsize=(18,10))
plt.scatter(X.Income, X.Account)输出:

请注意,现在我们还没有非常方便的标签来帮助我们针对每个类别训练模型。所以我们的例子变得更加现实了。我们需要想出一些方法来解决这个问题。幸运的是,我们现在知道可以使用聚类算法。
python
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
# X = StandardScaler().fit_transform(X.Income.values.reshape(-1,1))
kmeans = KMeans(n_clusters=5,random_state=0).fit(X)
python
plt.figure(figsize=(18,10))
plt.scatter(X.Income, X.Account, c=kmeans.labels_)输出:

K-Means 完美地完成了它的任务!
我们将为每个聚类构建其自己的线性回归。
python
set(kmeans.labels_)输出:
{np.int32(0), np.int32(1), np.int32(2), np.int32(3), np.int32(4)}
python
from sklearn.linear_model import LinearRegression
X, y = X.Income.values, X.Account.values
x_0, y_0 = X[kmeans.labels_ == 0], y[kmeans.labels_ == 0]
x_1, y_1 = X[kmeans.labels_ == 1], y[kmeans.labels_ == 1]
x_2, y_2 = X[kmeans.labels_ == 2], y[kmeans.labels_ == 2]
x_3, y_3 = X[kmeans.labels_ == 3], y[kmeans.labels_ == 3]
x_4, y_4 = X[kmeans.labels_ == 4], y[kmeans.labels_ == 4]
LR_0 = LinearRegression().fit(x_0.reshape(-1,1), y_0)
LR_1 = LinearRegression().fit(x_1.reshape(-1,1), y_1)
LR_2 = LinearRegression().fit(x_2.reshape(-1,1), y_2)
LR_3 = LinearRegression().fit(x_3.reshape(-1,1), y_3)
LR_4 = LinearRegression().fit(x_4.reshape(-1,1), y_4)让我们显示得到的结果
python
plt.figure(figsize=(18,10))
plt.scatter(X, y, c=kmeans.labels_)
plt.plot([100_000,200_000], [LR_0.predict([[100_000]]), LR_0.predict([[200_000]])])
plt.plot([0,30_000], [LR_1.predict([[0]]), LR_1.predict([[30_000]])])
plt.plot([200_000,300_000], [LR_2.predict([[200_000]]), LR_2.predict([[300_000]])])
plt.plot([0,50_000], [LR_3.predict([[0]]), LR_3.predict([[50_000]])])
plt.plot([50_000,100_000], [LR_4.predict([[50_000]]), LR_4.predict([[100_000]])])输出:
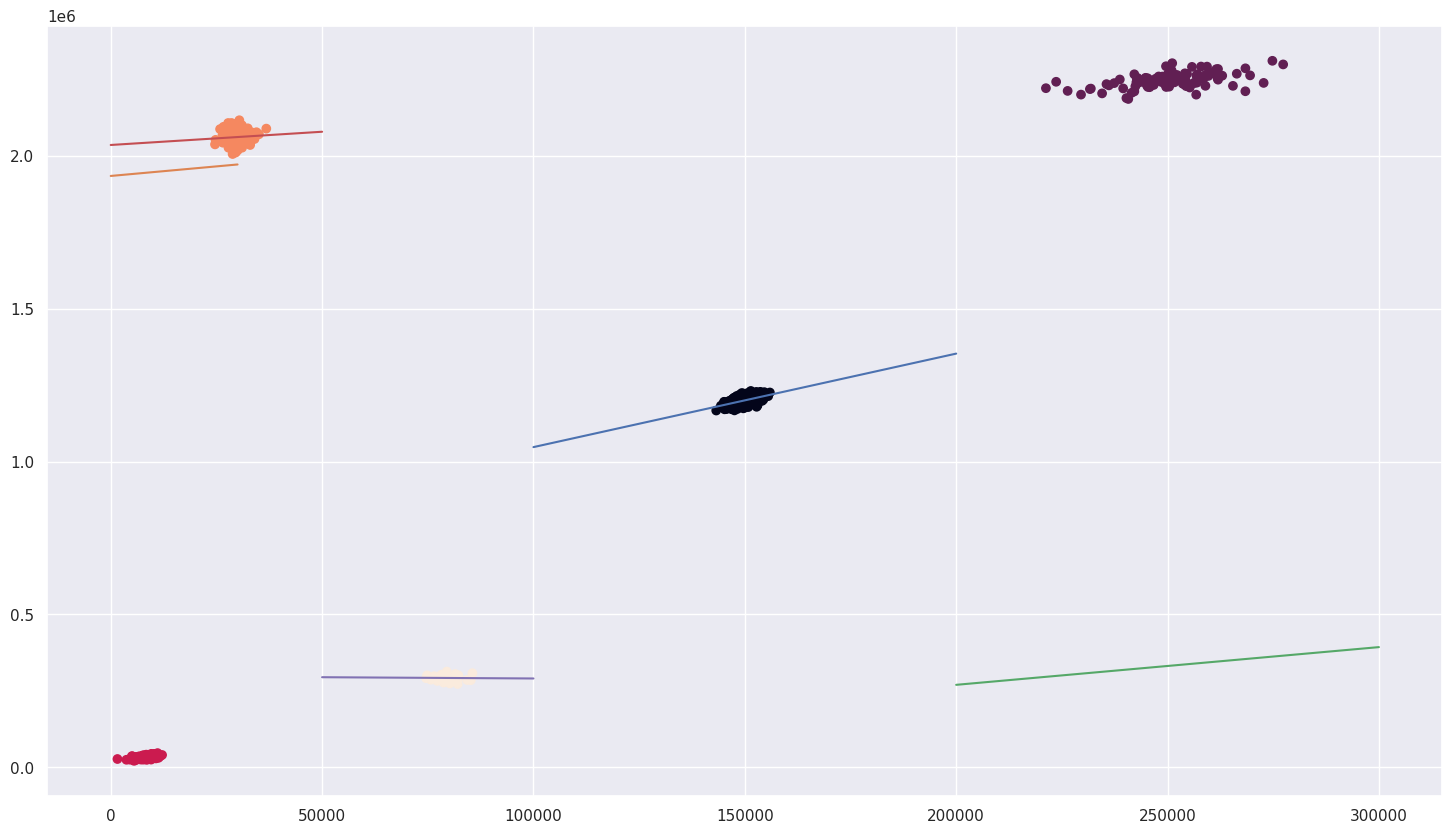
python
from sklearn.metrics import r2_score
print(f"r2_score cluster 0: {r2_score(y_0, LR_0.predict(x_0.reshape(-1,1)))}")
print(f"r2_score cluster 1: {r2_score(y_1, LR_1.predict(x_1.reshape(-1,1)))}")
print(f"r2_score cluster 2: {r2_score(y_2, LR_2.predict(x_2.reshape(-1,1)))}")
print(f"r2_score cluster 3: {r2_score(y_3, LR_3.predict(x_3.reshape(-1,1)))}")
print(f"r2_score cluster 4: {r2_score(y_4, LR_4.predict(x_4.reshape(-1,1)))}")输出:
r2_score cluster 0: 0.2747806800970829
r2_score cluster 1: 0.28099320642424697
r2_score cluster 2: 0.24097422328004658
r2_score cluster 3: 0.006983387523667006
r2_score cluster 4: 0.0006180165841759289
DBSCAN
DBSCAN 算法是另一种流行的聚类方法。它的优势在于,与 KMeans 算法不同,DBSCAN 算法理论上能够识别几乎任意几何形状的聚类结构。例如,KMeans 算法无法识别带状聚类和放射状聚类,而 DBSCAN 算法只要正确选择超参数,就能完美地完成这项任务。DBSCAN 算法还能独立检测数据中的异常值,并将其从已发现的聚类结构中排除。
DBSCAN 算法
数据集中的所有对象都会被聚类为内部 、边界 和异常值 。内部 是指位于半径为 ϵ ϵ ϵ 的小邻域内的对象,其中至少有 M M M 个其他对象。边界 是指位于内部对象邻域内的对象。异常值是指不位于内部或边界对象任何邻域内的对象。
- 设置算法的超参数:整数值 M M M 和较小的 ϵ ϵ ϵ
- 设置样本 U = { x i ∣ i = 0... N } U = \{x_i| i = 0...N\} U={xi∣i=0...N} 个未标记对象
- 当样本中存在未标记对象时:
- 随机选择一个未标记对象 x x x
- 如果 x x x 的邻域内有超过 M M M 个对象,则形成一个新的聚类 K K K,并将 x x x 邻域内的所有对象(包括 x x x 本身)标记为聚类 K K K 的对象。
- 对 x x x 邻域内的所有对象执行相同操作。
- 否则 将 x x x 标记为潜在异常值。
DBSCAN 算法可以在同一个 sklearn.cluster 模块中找到。让我们来看看它在著名的 moons 数据集上是如何工作的。
python
from matplotlib import pyplot as plt
from sklearn.datasets import make_moons
import seaborn as sns
sns.set_theme()
x, y = make_moons(n_samples=200, shuffle=True, noise=5e-2)
plt.scatter(x[:, 0], x[:, 1], c=y)输出:

该算法"看待"此数据集的方式有所不同:它没有初始划分为黑白两类聚类。让我们应用 DBSCAN 来获取实际的聚类标签。
python
plt.scatter(x[:, 0], x[:, 1])输出:
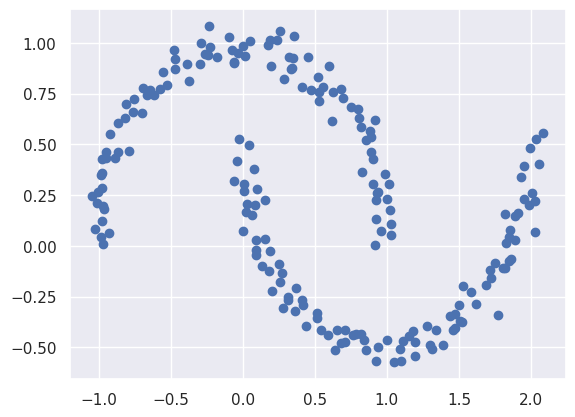
python
from sklearn.cluster import DBSCAN
clustering = DBSCAN(eps=0.25, min_samples=2).fit(x)
# 要访问聚类结果,需要访问 clustering.labels_ 字段
clust = clustering.labels_
plt.scatter(x[:, 0], x[:, 1], c=clust)输出:

聚类结果非常理想。但需要注意的是,这很大程度上取决于 eps 参数的正确选择。例如,如果我们稍微降低 eps,我们得到的聚类结果会比预期多得多:
python
clustering = DBSCAN(eps=0.1, min_samples=2).fit(x)
clust = clustering.labels_
plt.scatter(x[:, 0], x[:, 1], c=clust)输出:
 如果我们稍微增加它,那么所有的点将被分配到一个集群。
如果我们稍微增加它,那么所有的点将被分配到一个集群。
python
clustering = DBSCAN(eps=0.5, min_samples=2).fit(x)
clust = clustering.labels_
plt.scatter(x[:, 0], x[:, 1], c=clust)输出:

这是"DBSCAN"的一个重要限制。需要记住的是,与"KMeans"相比,更改超参数集并不能减轻我们与选择超参数相关的工作。尽管存在这种复杂性,"DBSCAN"仍然是一种非常有用的聚类算法,它使我们能够识别具有复杂规律性的聚类。