初识 二叉树

目录

• 树
• 什么是二叉树
• • 二叉树的五种状态
  • 满二叉树
  • 完全二叉树
  • 二叉排序树
  • 平衡二叉树
• 二叉树的遍历
• • [B3642 二叉树的遍历](#B3642 二叉树的遍历)
  • [P1305 新二叉树](#P1305 新二叉树)
• 二叉树的深度
• • [P4913 【深基16.例3】二叉树深度](#P4913 【深基16.例3】二叉树深度)
• 相关例题训练：

树

这是树（拍摄于郑州轻工业大学，第一次郑州轻工业新生赛~）

这是树的一些概念：

什么是二叉树

？？？

二叉树是n(n>=0)个节点的有限集合。

• 1.每个节点最多只有两个子树
• 2.左右子树不能颠倒
  （二叉树是有序树）

二叉树的五种状态

几种特殊的二叉树：

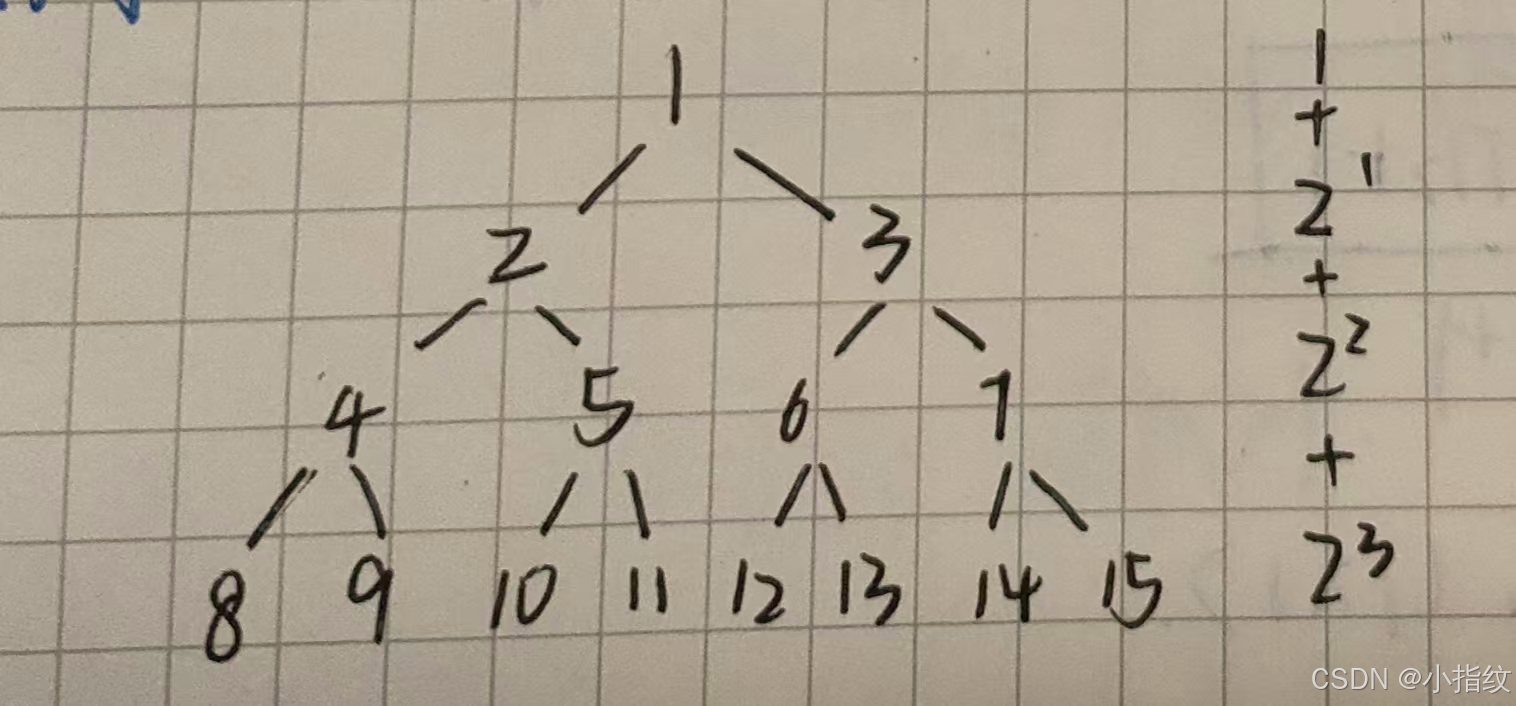
满二叉树

高度为h，且含有 2 h 2^h 2h-1个结点的二叉树
特点：

• 1.只有最后一层有叶子结点
• 2.不存在度为一的点
• 3.按层序从1开始编号结点i的左孩子为2i ,右孩子为2i+1
  

完全二叉树

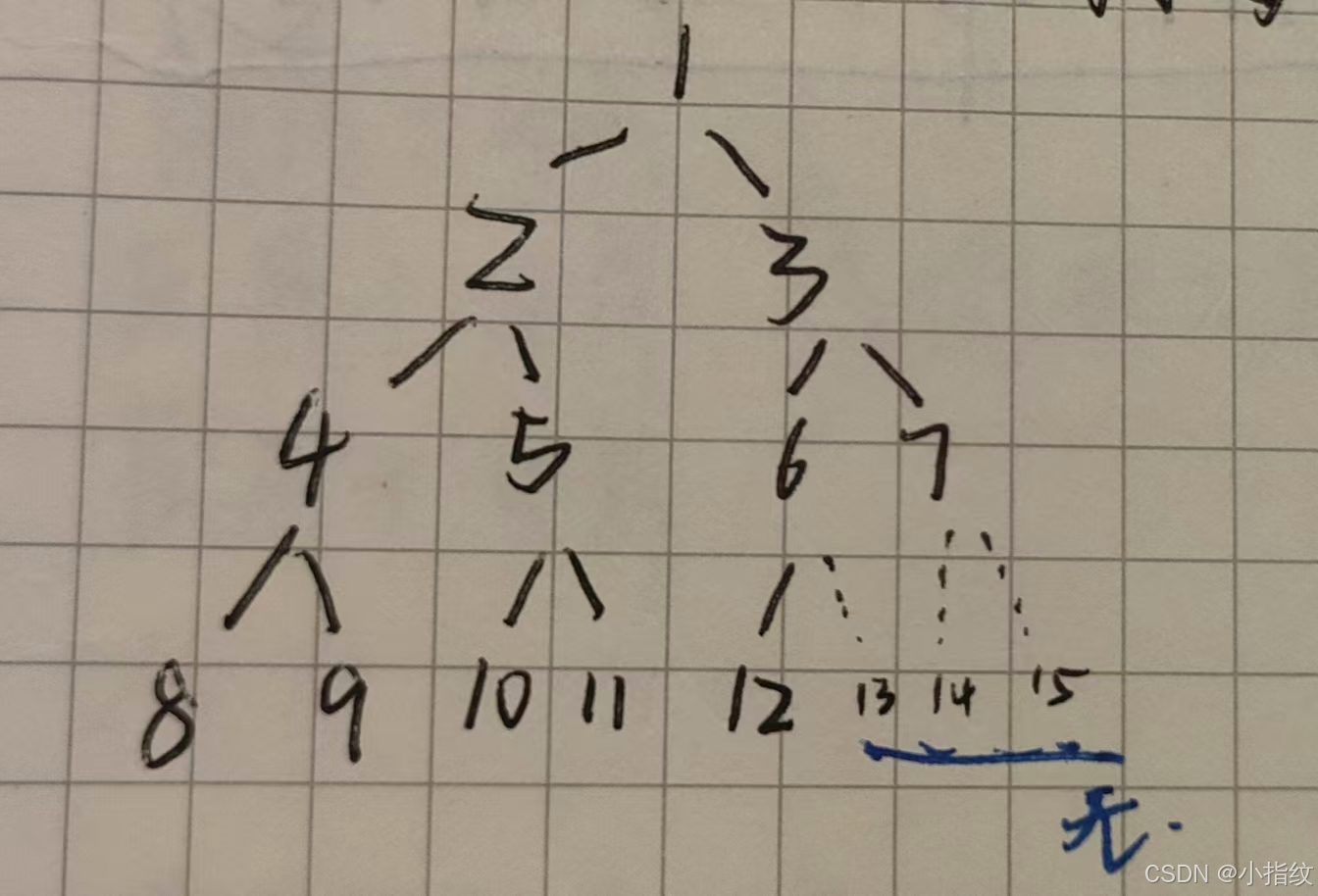
当且仅当其每个结点都与高度为h的满二叉树中编号问为1~n的结点一 一对应时成为完全二叉树。
特点

• 1.只有最后两层可能有叶子结点。
• 2.最多 只有一个度为1的结点。
• 3.按层序从1开始编号结点i的左孩子为2i ,右孩子为2i+1
  

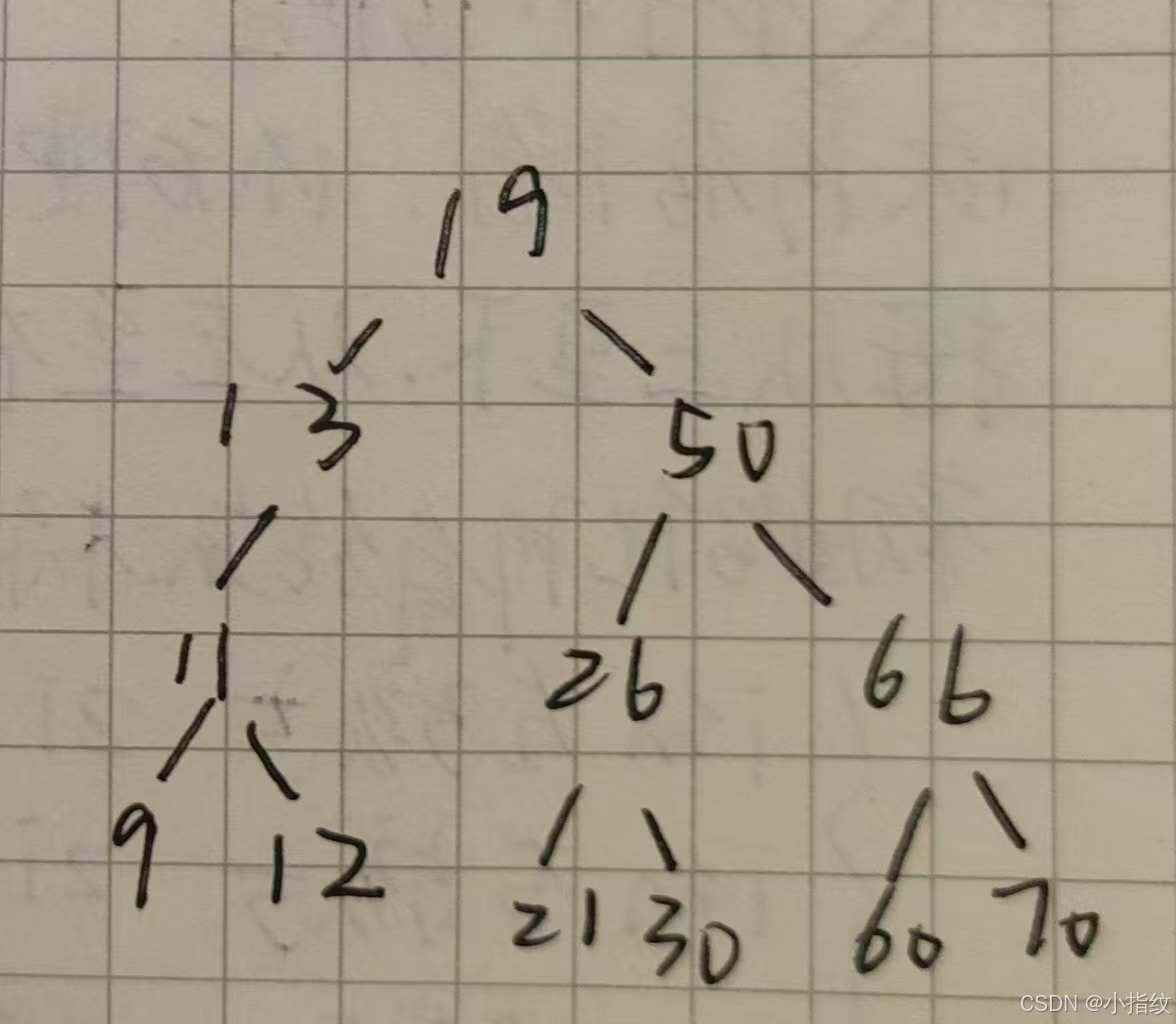
二叉排序树

左子树上所有结点的关键字均小于根节点的关键字
右子树上所有结点的关键字均大于根节点的关键字

左子树和右子树又分别时一颗二叉排序树

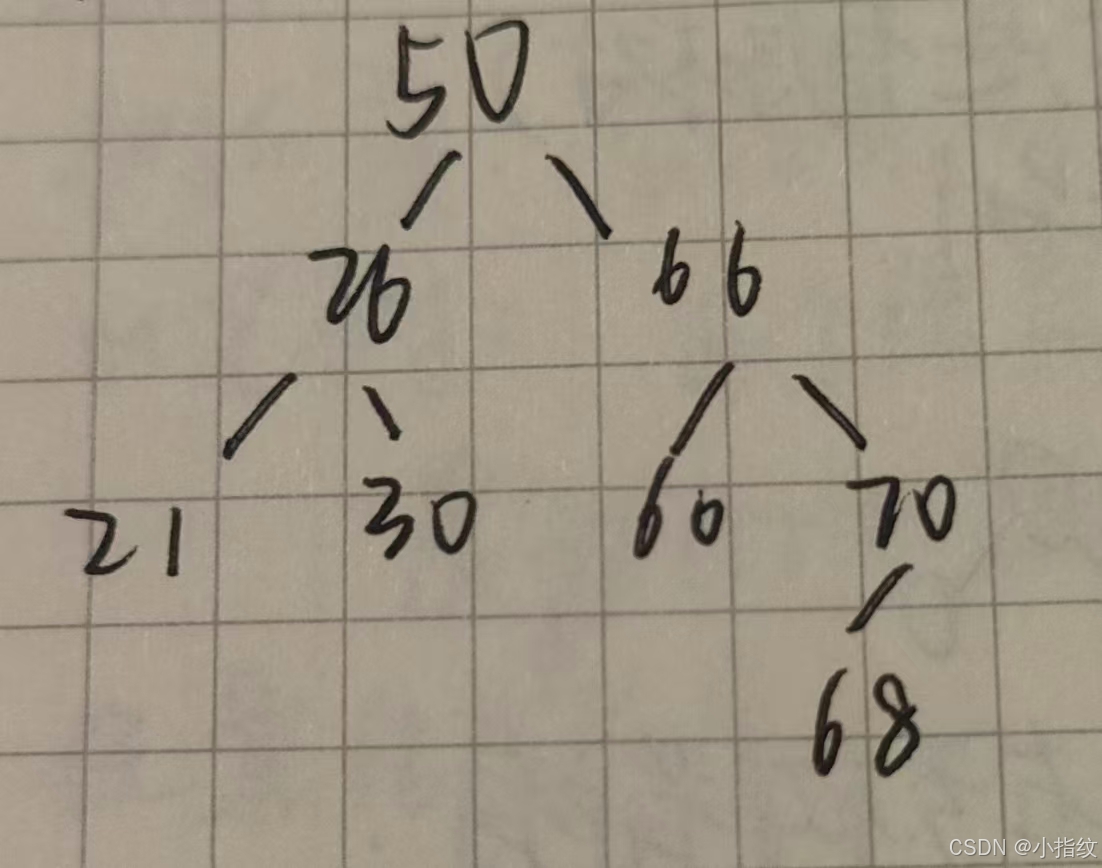
平衡二叉树

树上任一结点的左子树和右子树的深度之差不超过1

(有更高的搜索效率 )

二叉树的遍历

前序遍历

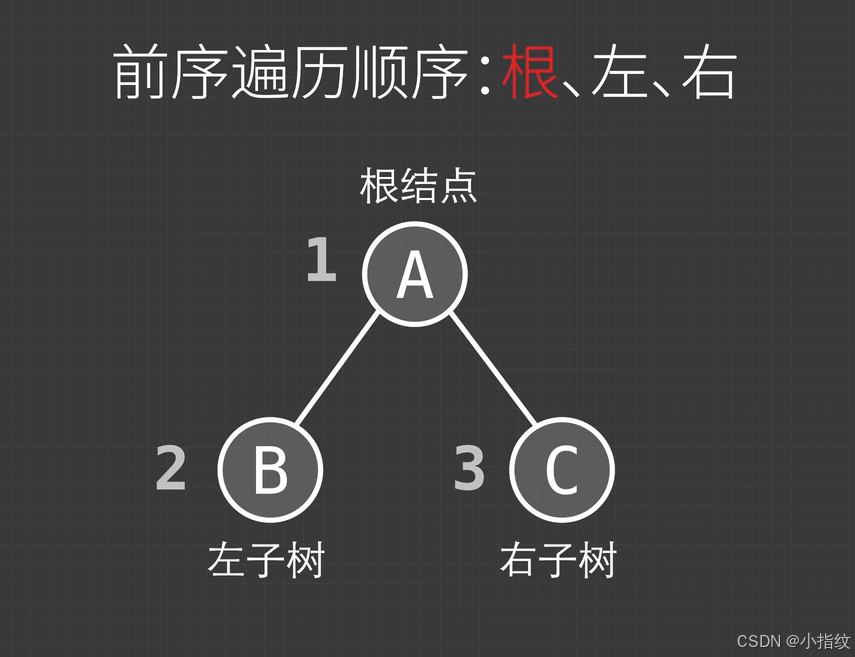
中序遍历

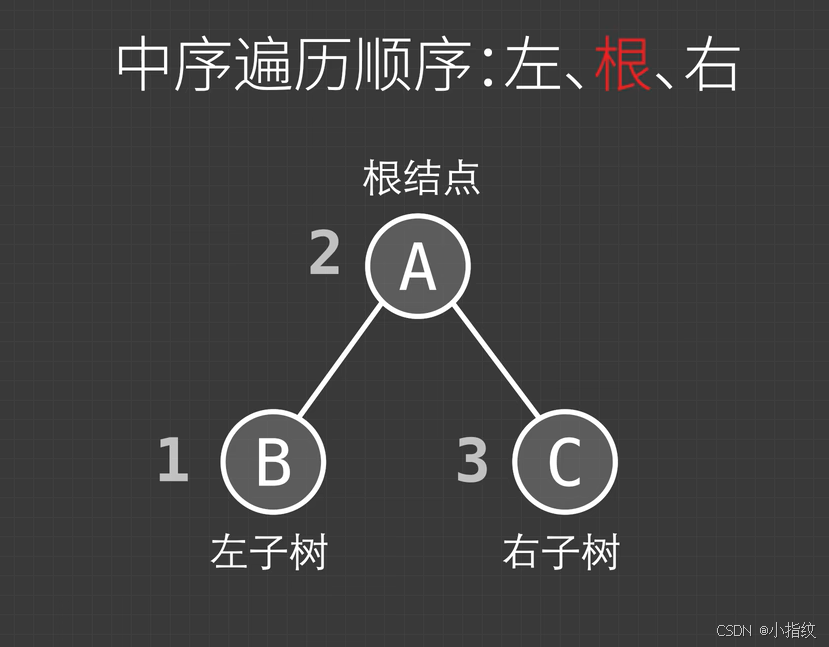
后序遍历

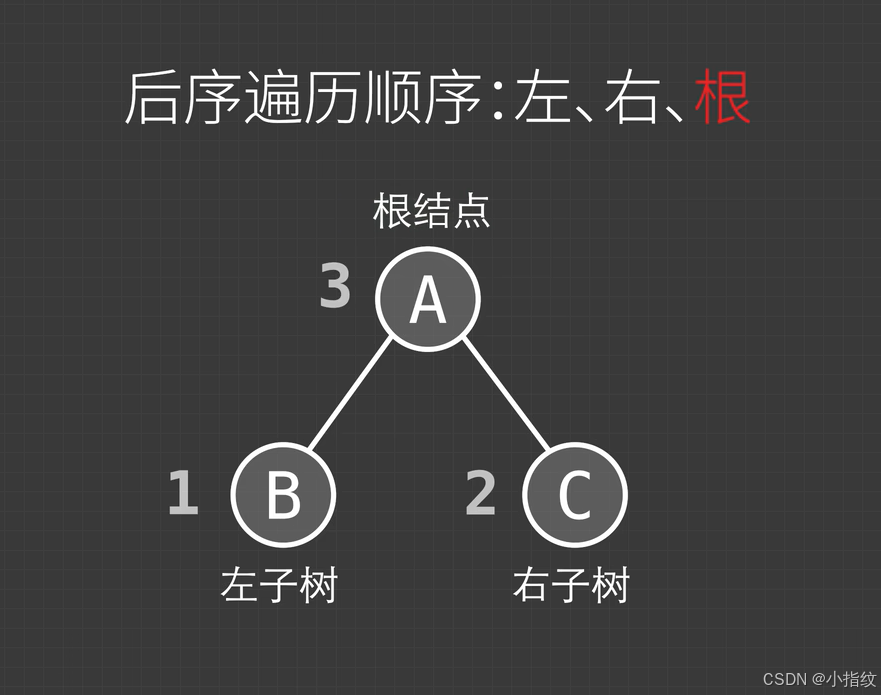
关于遍历二叉树，有一个巧妙的方法分享给大家。

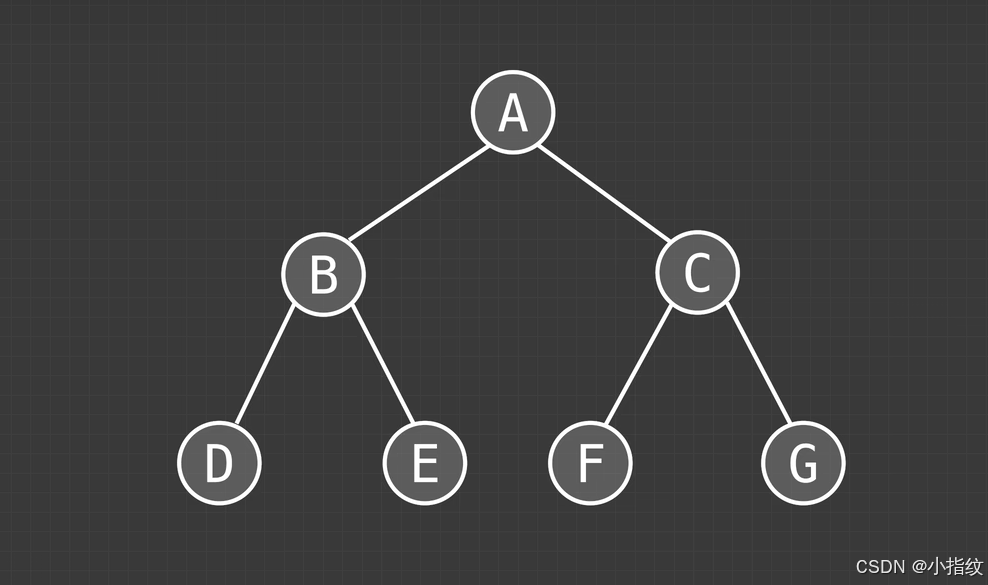
以下图为例：

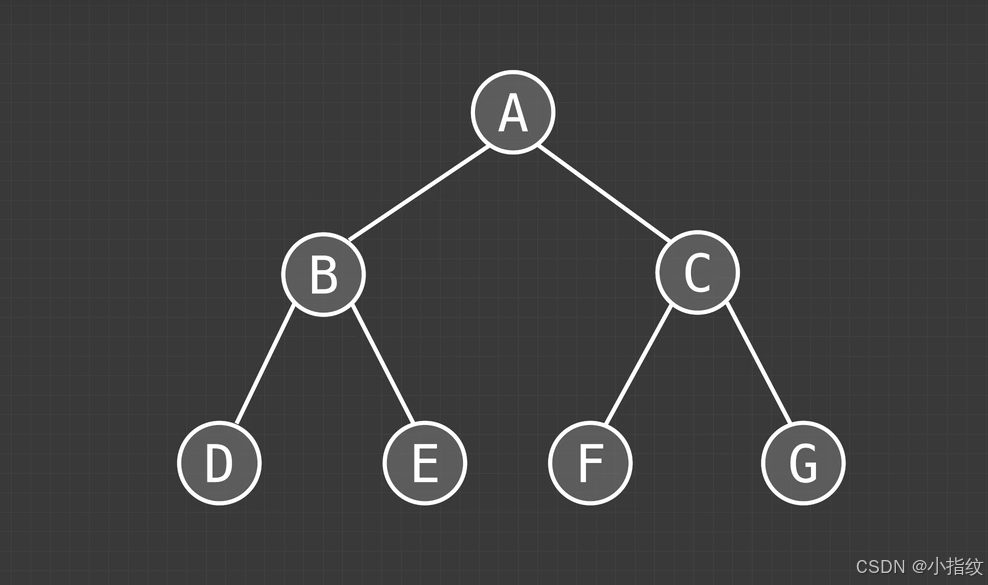
以中序遍历：左根右 为例：

我们可以先遍历最上边的ABC, 并给B和C的子节点留上位置

_ B _ A _ C _

然后再将B和C的子节点按左根右 的顺序填上去

就是这个顺序：DBEAFCG

同理，你可以练习一下：
先序遍历：ABDECFG
后序遍历：DEBFGCA

有了以上的基础，我们拿道题练练手吧！

B3642 二叉树的遍历

B3642 二叉树的遍历

题目描述

有一个 n ( n ≤ 1 0 6 ) n(n \le 10^6) n(n≤106) 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 n n n），建立一棵二叉树（根节点的编号为 1 1 1），如果是叶子结点，则输入 0 0。

建好树这棵二叉树之后，依次求出它的前序、中序、后序列遍历。

输入格式

第一行一个整数 n n n，表示结点数。

之后 n n n 行，第 i i i 行两个整数 l l l、 r r r，分别表示结点 i i i 的左右子结点编号。若 l = 0 l=0 l=0 则表示无左子结点， r = 0 r=0 r=0 同理。

输出格式

输出三行，每行 n n n 个数字，用空格隔开。

第一行是这个二叉树的前序遍历。

第二行是这个二叉树的中序遍历。

第三行是这个二叉树的后序遍历。

输入 #1

7
2 7
4 0
0 0
0 3
0 0
0 5
6 0

输出 #1

1 2 4 3 7 6 5
4 3 2 1 6 5 7
3 4 2 5 6 7 1

这是一道很模板的二叉树遍历练习题，很适合新手宝宝体质，按顺序根据前序中序和后续的遍历顺序，结合深搜就可以很容易的输出顺序啦~代码注释很详细！

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+6;
int n,l[N],r[N];//l和r分别存左子节点和右子节点
//前序遍历，根左右  
void a(int x)//前序遍历访问到第x号点 
{
	if(x==0)return ;//题目中说这个结点为0时表示无此结点
	//然后就是按照前序遍历
	cout<<x<<" ";//先输出根
	a(l[x]);//再输出左子结点
	a(r[x]);//最后输出右子节点	
} 
//中序遍历，左根右
void b(int x)//中序遍历访问到第x号点 
{
	if(x==0)return ;
	//中序遍历 
	b(l[x]);//先输出左子结点
	cout<<x<<" ";//再输出根
	b(r[x]);//最后输出右子节点	
} 
//后序遍历，左右根
void c(int x)//后序遍历访问到第x号点 
{
	if(x==0)return ;
	//后序遍历顺序 
	c(l[x]);//先输出左子结点
	c(r[x]);//再输出右子节点	
	cout<<x<<" ";//最后输出根
} 
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>l[i]>>r[i];//输入对应位置的左右节点 
	//前序遍历，根左右 
	a(1);//根节点从1开始遍历
	cout<<endl;//前序遍历完后要输出换行
	//中序遍历，左根右
	b(1);//根节点也是从1开始中序遍历
	cout<<endl;
	//后序遍历，左右根
	c(1);
	cout<<endl; 
	return 0;
} 

再来一道例题练练手吧！

P1305 新二叉树

P1305 新二叉树

题目描述

输入一串二叉树，输出其前序遍历。

输入格式

第一行为二叉树的节点数 n n n。( 1 ≤ n ≤ 26 1 \leq n \leq 26 1≤n≤26)

后面 n n n 行，每一个字母为节点，后两个字母分别为其左右儿子。特别地，数据保证第一行读入的节点必为根节点。

空节点用 * 表示

输出格式

二叉树的前序遍历。

输入 #1

6
abc
bdi
cj*
d**
i**
j**

输出 #1

abdicj

一道很基础的二叉树题，可以通过结构体 将这个二叉树建立起来，虽然题目中给的字符，但同样可以存储在结构体数组中 ，因为字符ACS码最大不超过128，所以数组只需开150就足够，然后可以利用深搜 ，将第一个节点传入dfs，依次搜索，当子节点不为 * 时才继续往下搜。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
struct node//简单的建树 
{
	char l,r;
}p[150];
int n;
void dfs(char bg)
{
	cout<<bg;
	if(p[bg].l !='*') dfs(p[bg].l);//如果不为空节点就接着往下搜 
	if(p[bg].r !='*') dfs(p[bg].r);
}
void solve()
{
	cin>>n;
	char a,x,y,bg;
	cin>>a>>x>>y;
	bg=a;//作为初始深搜的点 
	p[a].l =x,p[a].r =y;//左右子数 
	n-=1;
	while(n--)
	{
		cin>>a>>x>>y;
		p[a].l =x,p[a].r =y;
	}
	dfs(bg);
}
signed main()
{
	IOS;
	int _=1;
//	cin>>_;
	while(_--)
	solve();
	return 0;
}

---

二叉树的深度

二叉树深度简而言之就是这个二叉树最多有几层

比如这个二叉树，它的深度就是3

我们直接上例题感受一下吧！

P4913 【深基16.例3】二叉树深度

题目描述

有一个 n ( n ≤ 1 0 6 ) n(n \le 10^6) n(n≤106) 个结点的二叉树。给出每个结点的两个子结点编号（均不超过 n n n），建立一棵二叉树（根节点的编号为 1 1 1），如果是叶子结点，则输入 0 0。

建好这棵二叉树之后，请求出它的深度。二叉树的深度是指从根节点到叶子结点时，最多经过了几层。

输入格式

第一行一个整数 n n n，表示结点数。

之后 n n n 行，第 i i i 行两个整数 l l l、 r r r，分别表示结点 i i i 的左右子结点编号。若 l = 0 l=0 l=0 则表示无左子结点， r = 0 r=0 r=0 同理。

输出格式

一个整数，表示最大结点深度。

输入 #1

7
2 7
3 6
4 5
0 0
0 0
0 0
0 0

输出 #1

4

思路分析

我们可以先利用结构体读入这个二叉树

• 拥有左子节点和右子节点两个参数的结构体

• 开n范围的结构体数组
  搜索（dfs)

• 状态：当前走到什么编号的节点 以及当前的深度

• 终止条件：走到0号节点（更新最大深度)

• 走到哪里去？当前所在编号的节点的左右子节点
  输出最大深度

AC代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e6+6;
struct node//建树 
{
	int l,r;
}p[N];
int n,ans=INT_MIN;//ans用来记录树的最大深度 
void dfs(int x,int h)
{
	//终止条件：子节点为0时 
	ans=max(ans,h);//更新最大值 
	//走到哪里去
	if(p[x].l)//如果左子节点不为0 
	dfs(p[x].l,h+1);
	if(p[x].r)//如果右子节点不为0 
	dfs(p[x].r,h+1); 
}
void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>p[i].l>>p[i].r;
	dfs(1,1);//传入最初所在位置和最初深度
	cout<<ans; 
}
signed main()
{
	IOS;
	int _=1;
//	cin>>_;
	while(_--)
	solve();
	return 0;
}

---

相关例题训练：

P3884 [JLOI2009] 二叉树问题