OpenCV 官翻5 - 机器学习

伊织code2025-07-20 14:08

文章目录

K-最近邻算法

https://docs.opencv.org/4.x/d0/d72/tutorial_py_knn_index.html

了解kNN算法的基本原理

现在让我们在OpenCV中使用kNN实现数字识别OCR

生成于2025年4月30日 星期三 23:08:43 为OpenCV项目

理解k-最近邻算法

https://docs.opencv.org/4.x/d5/d26/tutorial_py_knn_understanding.html

目标

在本章中，我们将理解k-最近邻（kNN）算法的概念。

理论

kNN（k-最近邻）是监督学习中最简单的分类算法之一。其核心思想是在特征空间中搜索测试数据的最接近匹配项。我们通过下图来理解这一概念。

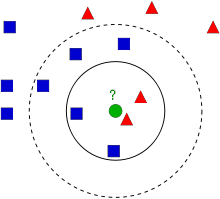
图中展示了两个家族：蓝色方块与红色三角。每个家族被称为一个类别 （Class）。它们的房屋分布在城镇地图上，这个地图就是特征空间（Feature Space）。你可以将特征空间视为所有数据投影的空间。例如，一个二维坐标系中，每个数据点有两个特征：x坐标和y坐标。你可以在二维坐标系中表示这个数据点，对吧？如果有三个特征，就需要三维空间。扩展到N个特征时，就需要N维空间------这就是特征空间。在我们的图中，可以将其视为具有两个特征的二维案例。

现在假设一个新成员来到城镇并建造了新家（图中绿色圆圈所示）。他需要被归类到蓝色或红色家族（即类别 中）。这个过程称为分类（Classification）。具体如何分类呢？既然我们使用kNN算法，就来应用它。

最简单的方法是检查谁是他的最近邻居。显然，图中最近的是红色三角家族成员，因此他被归类为红色三角。这种方法称为最近邻分类 （Nearest Neighbour classification），因为分类仅取决于最近邻居。

但这种方法存在问题！虽然红色三角是最近邻居，但如果附近有许多蓝色方块呢？此时蓝色方块在该区域的影响力更大，仅检查最近一个邻居就不够了。更好的做法是检查k个 最近家族，然后根据多数决原则归类新成员。例如图中k=3时，新成员有两个红色邻居和一个蓝色邻居（虽然有两个蓝色邻居等距，但k=3只能选一个），因此仍归为红色家族。但如果k=7呢？此时他有5个蓝色邻居和2个红色邻居，应归为蓝色家族。结果会随k值变化而变化。注意：若k为偶数（如k=4），可能出现平局（2红 vs 2蓝），此时需要额外的平局处理方法。因此，这种方法称为k-最近邻分类 （k-Nearest Neighbour classification），因为分类取决于k个最近邻居。

进一步思考：kNN中虽然考虑k个邻居，但所有邻居的权重相同是否合理？例如k=4平局时，两个红色邻居实际比蓝色邻居更接近新成员，他更应归为红色家族。如何数学化表达这一点？我们可以根据邻居与新成员的距离赋予不同权重：距离越近权重越高，越远则越低。然后分别计算各家族的总权重，将新成员归类到总权重更高的家族。这称为改进版kNN 或加权kNN（weighted kNN）。

通过这个例子，我们可以总结出哪些关键点？

  • 计算与存储需求：为了找到最近邻居，需要计算新成员与所有现有房屋的距离，因此必须存储整个城镇的房屋信息。如果房屋和家族数量庞大，将消耗大量内存和计算时间。
  • 训练过程：几乎不需要任何"训练"或准备时间。"学习"仅涉及在测试和分类前记忆（存储）数据。

接下来，我们将在OpenCV中实践这一算法。

OpenCV中的kNN算法

我们将做一个简单的示例，包含两个家族（类别），就像上面描述的那样。然后在下一章中，我们会实现一个更完善的案例。

这里，我们将红色家族标记为Class-0 （用数字0表示），蓝色家族标记为Class-1（用数字1表示）。我们创建了25个邻居点（即25个训练数据），并将每个点标记为Class-0或Class-1的成员。这一步骤可以通过NumPy的随机数生成器来实现。

接着，我们借助Matplotlib进行可视化绘制。红色邻居点显示为红色三角形，蓝色邻居点显示为蓝色方块。

python 复制代码 
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

# Feature set containing (x,y) values of 25 known/training data
trainData = np.random.randint(0,100,(25,2)).astype(np.float32)

# Label each one either Red or Blue with numbers 0 and 1
responses = np.random.randint(0,2,(25,1)).astype(np.float32)

# Take Red neighbours and plot them
red = trainData[responses.ravel()==0]
plt.scatter(red[:,0],red[:,1],80,'r','^')

# Take Blue neighbours and plot them
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:,0],blue[:,1],80,'b','s')

plt.show()

您将得到类似于我们第一张图片的结果。由于使用了随机数生成器，每次运行代码时都会得到不同的数据。

接下来初始化kNN算法，并传入trainData和responses进行训练。（在底层，它会构建一个搜索树：更多信息请参阅下方的"附加资源"部分。）

然后我们将引入一个新成员，并通过OpenCV中的kNN帮助将其分类到某个家族。在运行kNN之前，需要了解测试数据（新成员数据）的一些特性。数据应该是一个大小为...的浮点数组。接着我们寻找新成员的最近邻居。可以指定k值：即需要多少个邻居（这里我们使用3）。它会返回：

  1. 根据之前介绍的kNN理论赋予新成员的标签。如果只想使用"最近邻"算法，只需设置k=1。
  2. k个最近邻居的标签。
  3. 新成员与每个最近邻居的对应距离。

让我们看看实际效果。新成员用绿色标记。

python 复制代码 
newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'g','o')

knn = cv.ml.KNearest_create()
knn.train(trainData, cv.ml.ROW_SAMPLE, responses)
ret, results, neighbours ,dist = knn.findNearest(newcomer, 3)

print( "result:  {}\n".format(results) )
print( "neighbours:  {}\n".format(neighbours) )
print( "distance:  {}\n".format(dist) )

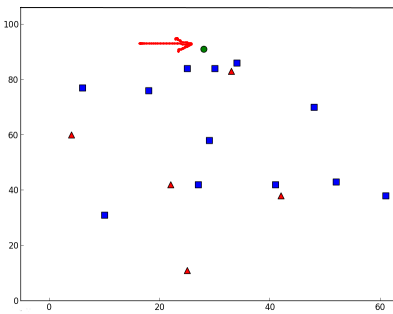
plt.show()

我得到了以下结果：

python 复制代码 
result:  [[ 1.]]
neighbours:  [[ 1.  1.  1.]]
distance:  [[ 53.  58.  61.]]

这表明我们新成员的3个最近邻居都来自Blue家族。因此，他被标记为Blue家族的一员。从下方图表可以明显看出：

如果有多个新成员（测试数据），你可以将它们作为数组传入。相应的结果也会以数组形式返回。

python 复制代码 
# 10 new-comers
newcomers = np.random.randint(0,100,(10,2)).astype(np.float32)
ret, results,neighbours,dist = knn.findNearest(newcomer, 3)
# The results also will contain 10 labels.

其他资源

  1. NPTEL 关于模式识别的笔记，第11章
  2. 维基百科关于最近邻搜索的文章
  3. 维基百科关于k-d树的文章

练习

  1. 尝试用更多类别和不同的k值重复上述操作。在相同的二维特征空间中，随着类别数量增加，选择k值是否变得更困难？

使用kNN进行手写数据OCR

https://docs.opencv.org/4.x/d8/d4b/tutorial_py_knn_opencv.html

目标

在本章中：

  • 我们将运用kNN算法知识构建一个基础的OCR（光学字符识别）应用程序。
  • 我们将在OpenCV自带的数字和字母数据集上测试该应用。

手写数字OCR识别

我们的目标是构建一个能够识别手写数字的应用程序。为此，我们需要准备训练数据和测试数据。OpenCV自带了一个包含5000个手写数字样本的图像文件digits.png（位于opencv/samples/data/文件夹中），每个数字各有500个样本。每个数字都是20x20像素的图像。

首先我们需要将这个图像分割成5000个独立的数字图像。接着，将每个20x20的数字图像展平为包含400个像素的单行数据，这就是我们的特征集------即所有像素的强度值。这是我们能创建的最简单的特征集。

我们将每个数字的前250个样本作为训练数据，剩下的250个样本作为测试数据。现在让我们先来准备这些数据。

python 复制代码 
import numpy as np
import cv2 as cv

img = cv.imread('digits.png')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)

# Now we split the image to 5000 cells, each 20x20 size
cells = [np.hsplit(row,100) for row in np.vsplit(gray,50)]

# Make it into a Numpy array: its size will be (50,100,20,20)
x = np.array(cells)

# Now we prepare the training data and test data
train = x[:,:50].reshape(-1,400).astype(np.float32) # Size = (2500,400)
test = x[:,50:100].reshape(-1,400).astype(np.float32) # Size = (2500,400)

# Create labels for train and test data
k = np.arange(10)
train_labels = np.repeat(k,250)[:,np.newaxis]
test_labels = train_labels.copy()

# Initiate kNN, train it on the training data, then test it with the test data with k=1
knn = cv.ml.KNearest_create()
knn.train(train, cv.ml.ROW_SAMPLE, train_labels)
ret,result,neighbours,dist = knn.findNearest(test,k=5)

# Now we check the accuracy of classification
# For that, compare the result with test_labels and check which are wrong
matches = result==test_labels
correct = np.count_nonzero(matches)
accuracy = correct*100.0/result.size
print( accuracy )

我们的基础OCR应用已经准备就绪。这个特定示例的准确率达到了91%。提高准确率的一个方法是增加更多训练数据，特别是针对那些错误率较高的数字。

与其每次启动应用时都重新寻找训练数据，更好的做法是将数据保存下来。这样下次使用时，可以直接从文件中读取数据并开始分类。我们可以借助一些NumPy函数来实现，比如np.savetxt、np.savez、np.load等。更多细节请查阅NumPy文档。

python 复制代码 
# Save the data
np.savez('knn_data.npz',train=train, train_labels=train_labels)

# Now load the data
with np.load('knn_data.npz') as data:
    print( data.files )
    train = data['train']
    train_labels = data['train_labels']

在我的系统中，内存占用约为4.4 MB。由于我们使用强度值（uint8数据）作为特征，最好先将数据转换为np.uint8格式再保存。这种情况下仅占用1.1 MB空间。加载时，可以将其转换回float32格式。

英文字母的OCR识别

接下来我们将对英文字母进行同样的处理，但在数据和特征集方面略有不同。这里OpenCV没有使用图像，而是提供了一个数据文件letter-recognition.data，位于opencv/samples/cpp/目录下。如果打开这个文件，你会看到20000行数据，乍看可能像乱码。实际上，每一行的第一列是一个字母（即我们的标签），随后的16个数字是不同的特征值。这些特征来自UCI机器学习库，具体特征说明可以参考这个页面。

由于共有20000个样本，我们取前10000个作为训练样本，剩下的10000个作为测试样本。需要将字母转换为ASCII字符，因为我们无法直接处理字母数据。

python 复制代码 
import cv2 as cv
import numpy as np

# Load the data and convert the letters to numbers
data= np.loadtxt('letter-recognition.data', dtype= 'float32', delimiter = ',',
                    converters= {0: lambda ch: ord(ch)-ord('A')})

# Split the dataset in two, with 10000 samples each for training and test sets
train, test = np.vsplit(data,2)

# Split trainData and testData into features and responses
responses, trainData = np.hsplit(train,[1])
labels, testData = np.hsplit(test,[1])

# Initiate the kNN, classify, measure accuracy
knn = cv.ml.KNearest_create()
knn.train(trainData, cv.ml.ROW_SAMPLE, responses)
ret, result, neighbours, dist = knn.findNearest(testData, k=5)

correct = np.count_nonzero(result == labels)
accuracy = correct*100.0/10000
print( accuracy )

准确率达到93.22%。如需进一步提高准确率，可以通过迭代增加更多数据来实现。

其他资源

  1. 维基百科关于光学字符识别的文章

练习

  1. 这里我们使用了k=5。如果尝试其他k值会发生什么？你能找到一个使准确率最大化（错误数量最小化）的k值吗？

支持向量机（SVM）

https://docs.opencv.org/4.x/d3/d02/tutorial_py_svm_index.html

生成于2025年4月30日 星期三 23:08:43，由doxygen 1.12.0生成

理解支持向量机(SVM)

OpenCV SVM基础教程

目标

在本章中，我们将直观地理解支持向量机(SVM)。

理论

线性可分数据

观察下图，其中包含两种数据：红色和蓝色。在kNN算法中，对于测试数据，我们通常需要计算它与所有训练样本的距离，并选择距离最小的样本。这种方法需要大量时间计算所有距离，并占用大量内存存储训练样本。但针对图中给出的数据，我们真的需要如此复杂的方法吗？

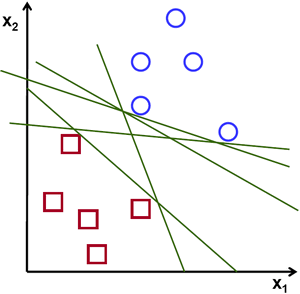
考虑另一种思路：找到一条能将两类数据划分到不同区域的直线。当获得新测试数据时，只需将其代入直线方程。若结果大于0，则属于蓝色组；否则属于红色组。我们将这条直线称为决策边界 。这种方法既简单又节省内存。这种能被直线（或高维空间中的超平面）分割的数据称为线性可分数据。

在上图中可以看到存在许多可能的划分直线。我们该选择哪一条？直观地说，直线应尽可能远离所有数据点。为什么？因为输入数据可能存在噪声，这些噪声不应影响分类准确性。因此，选择最远的直线能提供更强的抗噪能力。支持向量机（SVM）的核心思想就是找到与训练样本具有最大最小距离的直线（或超平面）。下图加粗的居中直线即为示例：

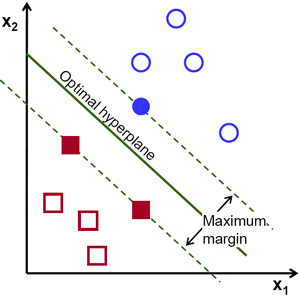
要找到这条决策边界，确实需要训练数据，但并非全部数据。只需那些靠近另一类别的样本就足够了。图中示例为一个蓝色实心圆和两个红色实心方块，这些样本称为支持向量 ，穿过它们的直线称为支撑平面。这些元素足以确定决策边界，无需处理全部数据，从而实现数据降维。

具体实现过程是：首先找到最能代表两类数据的超平面。例如，蓝色数据由表示，红色数据由表示，其中为权重向量 （决定决策边界的朝向），为特征向量，为偏置项（决定决策边界的位置）。决策边界被定义为这两个超平面的中间线，表达式为。支持向量到决策边界的最小距离为。间隔（margin）是该距离的两倍，我们需要最大化这个间隔。即通过以下约束条件最小化新函数：

其中为每个类别的标签，。

非线性可分数据

考虑一些无法用直线划分为两部分的数据。例如，假设一维数据中'X'位于-3和+3，而'O'位于-1和+1。显然这是线性不可分的。但存在解决此类问题的方法。如果我们用一个函数映射这个数据集，例如平方函数，'X'会映射到9，'O'映射到1，此时数据就变为线性可分的。

另一种方法是将一维数据转换为二维。我们可以使用平方函数进行映射，这样'X'变为(-3,9)和(3,9)，而'O'变为(-1,1)和(1,1)。此时数据同样线性可分。简而言之，低维空间中的非线性可分数据在高维空间中更有可能变为线性可分。

一般来说，我们可以将d维空间中的点映射到D维空间，以检验线性可分的可能性。有一种方法能通过在低维输入（特征）空间中进行计算，来帮助计算高维（核）空间中的点积。以下示例可以说明这一点：

考虑二维空间中的两个点和。设为一个映射函数，将二维点映射到三维空间如下：

我们定义一个核函数来计算两点间的点积，如下所示：

这意味着，三维空间中的点积可以通过二维空间中的平方点积来实现。这种方法可以推广到更高维空间。因此，我们可以从低维数据计算出高维特征。一旦完成映射，我们就得到了一个高维空间。

除了这些概念外，还存在误分类的问题。仅找到具有最大边界的决策边界是不够的，我们还需要考虑误分类误差。有时，可能找到一个边界较小但误分类较少的决策边界。无论如何，我们需要调整模型，使其在减少误分类的同时找到最大边界的决策边界。优化标准修改如下：

下图展示了这一概念。为训练数据中的每个样本定义一个新参数，即从样本到其正确决策区域的距离。对于未被误分类的样本，它们落在对应的支持平面上，因此距离为零。

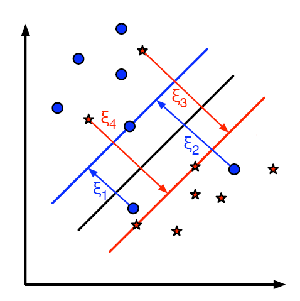
因此，新的优化问题为：

如何选择参数C？显然，答案取决于训练数据的分布。虽然没有通用答案，但以下规则值得参考：

  • 较大的C值会得到误分类较少但边界较小的解。此时误分类的代价较高，因为优化的目标是最小化参数，所以允许的误分类较少。
  • 较小的C值会得到边界较大但分类误差更多的解。此时优化过程不太关注求和项，而更侧重于寻找具有较大边界的超平面。

其他资源

  1. NPTEL 关于统计模式识别的笔记，第25-29章

使用支持向量机(SVM)进行手写数据OCR识别

原文链接

目标

在本章中

  • 我们将重新探讨手写数据OCR，但这次使用SVM替代kNN算法。

手写数字的OCR识别

在kNN算法中，我们直接使用像素强度作为特征向量。这次我们将采用方向梯度直方图(HOG)作为特征向量。

在计算HOG之前，我们会先利用二阶矩对图像进行去歪斜处理。因此首先定义**deskew()**函数，该函数接收数字图像并校正其倾斜。以下是deskew()函数的实现：

def deskew(img):

m = cv.moments(img)

if abs(m['mu02']) < 1e-2:

return img.copy()

skew = m['mu11']/m['mu02']

M = np.float32([[1, skew, -0.5SZ skew], [0, 1, 0]])

img = cv.warpAffine(img,M,(SZ, SZ),flags=affine_flags)

return img

下图展示了上述去歪斜函数应用于数字"0"的效果。左图为原始图像，右图为校正后的图像。

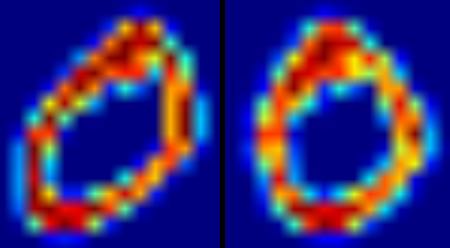
接下来需要计算每个单元格的HOG描述符。具体步骤为：

  1. 计算每个单元格在X和Y方向的Sobel导数
  2. 计算每个像素点的梯度幅值和方向
  3. 将梯度方向量化为16个整数值
  4. 将图像划分为四个子区域
  5. 对每个子区域，计算16维的加权方向直方图（权重为幅值）
  6. 四个子区域的16维向量共同组成64维特征向量

这个64维的特征向量将用于训练我们的模型。

python 复制代码 
def hog(img):
    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    mag, ang = cv.cartToPolar(gx, gy)
    bins = np.int32(bin_n*ang/(2*np.pi))    # quantizing binvalues in (0...16)
    bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
    mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
    hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
    hist = np.hstack(hists)     # hist is a 64 bit vector
    return hist

最后，与之前的情况类似，我们首先将大型数据集分割为单独的单元格。每个数字保留250个单元格作为训练数据，剩余的250个数据则留作测试。完整代码如下所示，你也可以从这里下载：

python 复制代码 
#!/usr/bin/env python

import cv2 as cv
import numpy as np

SZ=20
bin_n = 16 # Number of bins

affine_flags = cv.WARP_INVERSE_MAP|cv.INTER_LINEAR

def deskew(img):
    m = cv.moments(img)
    if abs(m['mu02']) < 1e-2:
        return img.copy()
    skew = m['mu11']/m['mu02']
    M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])
    img = cv.warpAffine(img,M,(SZ, SZ),flags=affine_flags)
    return img

def hog(img):
    gx = cv.Sobel(img, cv.CV_32F, 1, 0)
    gy = cv.Sobel(img, cv.CV_32F, 0, 1)
    mag, ang = cv.cartToPolar(gx, gy)
    bins = np.int32(bin_n*ang/(2*np.pi))    # quantizing binvalues in (0...16)
    bin_cells = bins[:10,:10], bins[10:,:10], bins[:10,10:], bins[10:,10:]
    mag_cells = mag[:10,:10], mag[10:,:10], mag[:10,10:], mag[10:,10:]
    hists = [np.bincount(b.ravel(), m.ravel(), bin_n) for b, m in zip(bin_cells, mag_cells)]
    hist = np.hstack(hists)     # hist is a 64 bit vector
    return hist

img = cv.imread(cv.samples.findFile('digits.png'),0)
if img is None:
    raise Exception("we need the digits.png image from samples/data here !")

cells = [np.hsplit(row,100) for row in np.vsplit(img,50)]

# First half is trainData, remaining is testData
train_cells = [ i[:50] for i in cells ]
test_cells = [ i[50:] for i in cells]

deskewed = [list(map(deskew,row)) for row in train_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
trainData = np.float32(hogdata).reshape(-1,64)
responses = np.repeat(np.arange(10),250)[:,np.newaxis]

svm = cv.ml.SVM_create()
svm.setKernel(cv.ml.SVM_LINEAR)
svm.setType(cv.ml.SVM_C_SVC)
svm.setC(2.67)
svm.setGamma(5.383)

svm.train(trainData, cv.ml.ROW_SAMPLE, responses)
svm.save('svm_data.dat')

deskewed = [list(map(deskew,row)) for row in test_cells]
hogdata = [list(map(hog,row)) for row in deskewed]
testData = np.float32(hogdata).reshape(-1,bin_n*4)
result = svm.predict(testData)[1]

mask = result==responses
correct = np.count_nonzero(mask)
print(correct*100.0/result.size)

这项特殊技术让我获得了接近94%的准确率。您可以尝试调整SVM各项参数的不同取值，以检验是否能达到更高的准确率。或者，您也可以阅读该领域的技术论文并尝试实现其中的方法。

附加资源

  1. 方向梯度直方图视频

练习

  1. OpenCV 示例中包含 digits.py 文件，该文件对上述方法进行了轻微改进以获得更好的结果。示例中还包含相关参考资料。请查阅并理解该代码。

K-Means 聚类

https://docs.opencv.org/4.x/d9/d70/tutorial_py_kmeans_index.html

阅读以获得对 K-Means 聚类的直观理解

现在让我们尝试 OpenCV 中的 K-Means 函数

由 doxygen 1.12.0 生成于 2025 年 4 月 30 日 星期三 23:08:43，用于 OpenCV

理解K-Means聚类算法

https://docs.opencv.org/4.x/de/d4d/tutorial_py_kmeans_understanding.html

目标

在本章中，我们将理解K-Means聚类算法的概念及其工作原理。

理论

我们将通过一个常用示例来处理这个问题。

T恤尺码问题

设想一家公司即将向市场推出新款T恤。显然，他们需要生产不同尺码的款式以满足各类体型人群的需求。为此，公司收集了人们的身高和体重数据，并将其绘制在如下图表中：

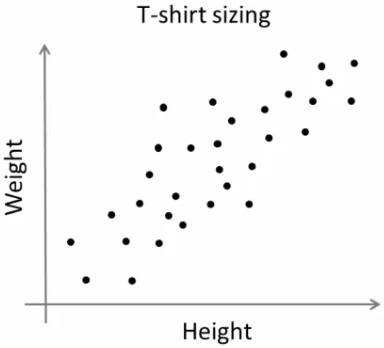
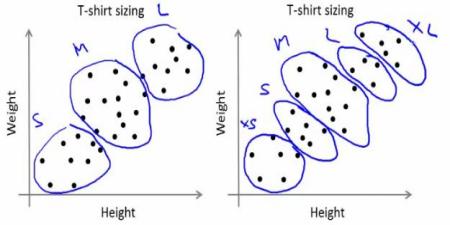
由于无法生产所有尺码的T恤，公司决定将人群划分为小号、中号和大号三类，仅生产这三种通用尺码来覆盖所有用户。这种人群分组可以通过k-means聚类算法实现，该算法能计算出最优的三个尺码方案以满足大多数需求。若效果不理想，公司还可以将人群划分为更多组别（例如五组）并依此类推。参考下图：

工作原理

该算法是一个迭代过程。我们将借助图片逐步解释其运作机制。

假设有如下数据集（可以视为T恤尺码问题），需要将其聚类为两组：

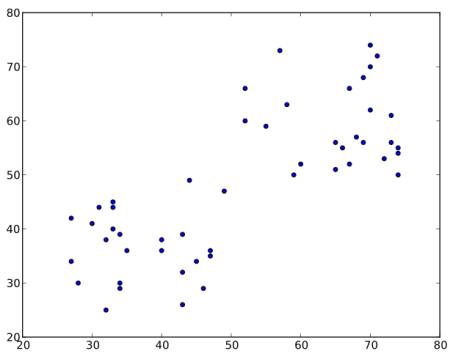
步骤1：算法随机选择两个质心（有时会直接选取任意两个数据点作为初始质心）。

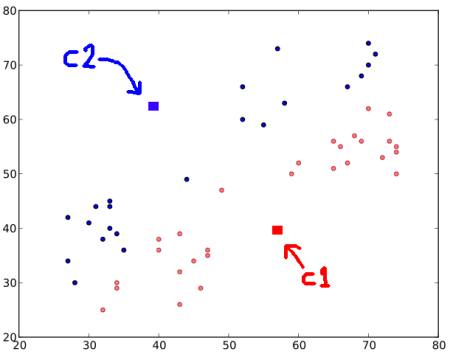
步骤2：计算每个点到两个质心的距离。若测试数据更接近第一个质心，则标记为"0"；若更接近第二个质心，则标记为"1"（若有更多质心则标记为"2"、"3"等）。在本例中，我们用红色标注所有"0"类数据，蓝色标注"1"类数据，得到如下结果：

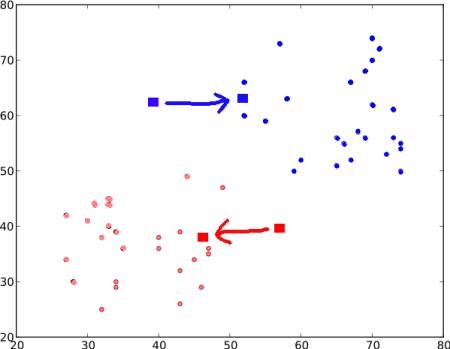
步骤3：接下来分别计算所有蓝色点和红色点的平均值，这两个均值点将成为新的质心（注意：图示仅为演示效果，非真实数值比例）。然后重复步骤2，用新质心重新标记数据。

更新后的结果如下：

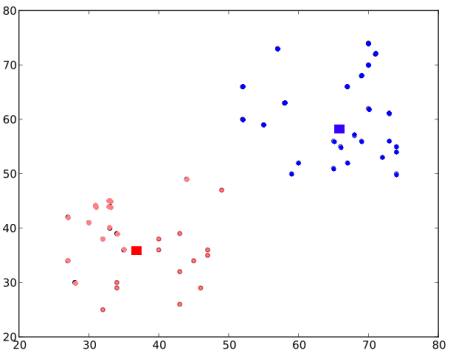
步骤2 和步骤3 将循环迭代，直到两个质心收敛至固定点（或达到停止条件，如最大迭代次数、指定精度等）。这些质心点的特性是：测试数据到其对应质心的距离之和最小，或者说两个质心之间的距离总和最小。

最终聚类结果如下图所示：

以上是对K-Means聚类算法的直观理解。如需更详细的数学解释，请参阅标准机器学习教材或附加资源中的链接。这只是K-Means的最基础原理，实际存在许多改进算法，例如初始质心选择方法、迭代加速技巧等。

补充资源

  1. 机器学习课程，Andrew Ng教授的系列视频讲座（部分图片来源于此）

OpenCV中的K-Means聚类算法

原文链接

目标

  • 学习使用 OpenCV 中的 cv.kmeans() 函数进行数据聚类

理解参数

输入参数

  1. samples ：数据类型应为np.float32，且每个特征需单独放在一列中。
  2. nclusters(K)：最终需要的聚类数量。
  3. criteria ：迭代终止条件。当满足此条件时，算法迭代停止。实际上，它应是一个包含3个参数的元组，格式为( type, max_iter, epsilon )：
    1. 终止条件的类型。有以下3种标志：
      • cv.TERM_CRITERIA_EPS - 如果达到指定的精度epsilon，则停止算法迭代。
      • cv.TERM_CRITERIA_MAX_ITER - 在达到指定的迭代次数max_iter后停止算法。
      • cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER - 当满足上述任一条件时停止迭代。
    2. max_iter - 指定最大迭代次数的整数。
    3. epsilon - 所需的精度。
  4. attempts：指定算法使用不同初始标签执行的次数。算法返回产生最佳紧凑度的标签，该紧凑度作为输出返回。
  5. flags ：此标志用于指定初始中心的选取方式。通常使用以下两种标志：cv.KMEANS_PP_CENTERS 和 cv.KMEANS_RANDOM_CENTERS。

输出参数

  1. compactness：表示各点到其对应中心点距离平方的总和。
  2. labels：这是一个标签数组（与前一篇文章中的'code'相同），其中每个元素被标记为'0'、'1'等。
  3. centers：这是聚类中心点组成的数组。

接下来我们将通过三个示例来演示如何应用K-Means算法。

1. 仅含单一特征的数据

假设你有一组仅包含一个特征的数据，即一维数据。例如，我们可以用T恤尺码问题作为例子，其中仅根据人们的身高来决定T恤的尺码。

因此，我们首先创建数据，并在Matplotlib中绘制它。

python 复制代码 
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

x = np.random.randint(25,100,25)
y = np.random.randint(175,255,25)
z = np.hstack((x,y))
z = z.reshape((50,1))
z = np.float32(z)
plt.hist(z,256,[0,256]),plt.show()

我们有一个大小为50的数组'z'，其值范围在0到255之间。我已将'z'重塑为列向量。当存在多个特征时，这种形式会更实用。接着，我将数据转换为np.float32类型。

得到如下图像：

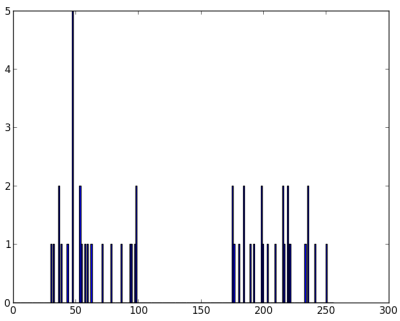
现在应用KMeans函数。在此之前需要指定停止条件。我的设定是：当算法运行10次迭代，或达到epsilon=1.0的精度时，停止算法并返回结果。

python 复制代码 
# Define criteria = ( type, max_iter = 10 , epsilon = 1.0 )
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)

# Set flags (Just to avoid line break in the code)
flags = cv.KMEANS_RANDOM_CENTERS

# Apply KMeans
compactness,labels,centers = cv.kmeans(z,2,None,criteria,10,flags)

这样我们就得到了紧凑性、标签和中心点。在本例中，我得到的中心点值为60和207。标签数组将与测试数据大小相同，其中每个数据点会根据其所属质心被标记为'0'、'1'、'2'等。现在我们根据这些标签将数据划分到不同的聚类中。

python 复制代码 
A = z[labels==0]
B = z[labels==1]

现在我们用红色绘制A，用蓝色绘制B，并用黄色标出它们的质心。

python 复制代码 
# Now plot 'A' in red, 'B' in blue, 'centers' in yellow
plt.hist(A,256,[0,256],color = 'r')
plt.hist(B,256,[0,256],color = 'b')
plt.hist(centers,32,[0,256],color = 'y')
plt.show()

我们得到的输出如下：

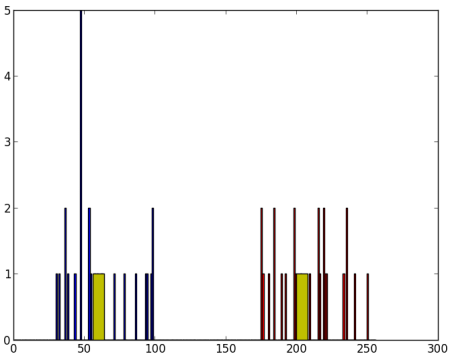
图像

2. 多特征数据

在前面的示例中，我们仅以身高作为T恤问题的特征。这里我们将同时考虑身高和体重这两个特征。

请注意，在之前的案例中，我们将数据转换为单列向量。每个特征按列排列，而每行对应一个输入测试样本。

例如，在本例中，我们设置了一个50x2的测试数据，包含50个人的身高和体重。第一列对应所有50个人的身高，第二列对应他们的体重。第一行包含两个元素，第一个是第一个人的身高，第二个是他的体重。其余行以此类推，对应其他人的身高和体重。参考下图：

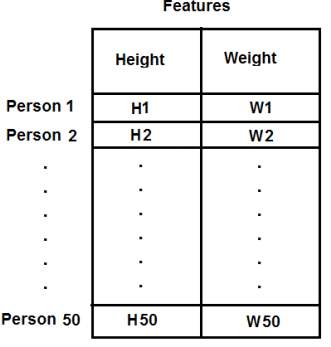
现在我将直接进入代码部分：

python 复制代码 
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

X = np.random.randint(25,50,(25,2))
Y = np.random.randint(60,85,(25,2))
Z = np.vstack((X,Y))

# convert to np.float32
Z = np.float32(Z)

# define criteria and apply kmeans()
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv.kmeans(Z,2,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)

# Now separate the data, Note the flatten()
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]

# Plot the data
plt.scatter(A[:,0],A[:,1])
plt.scatter(B[:,0],B[:,1],c = 'r')
plt.scatter(center[:,0],center[:,1],s = 80,c = 'y', marker = 's')
plt.xlabel('Height'),plt.ylabel('Weight')
plt.show()

以下是我们的输出结果：

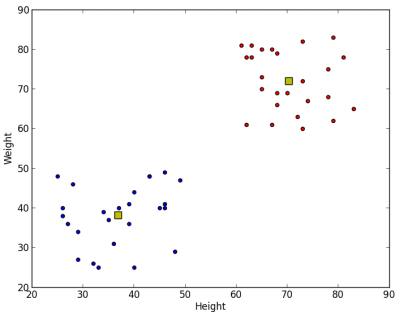
3. 色彩量化

色彩量化是指减少图像中颜色数量的过程。这样做的原因之一是为了降低内存占用。有时，某些设备可能存在限制，只能生成有限数量的颜色。在这些情况下，也需要进行色彩量化。这里我们使用k-means聚类算法来实现色彩量化。

这部分没有太多新内容需要解释。图像有三个特征，即R、G、B通道。因此我们需要将图像重塑为Mx3大小的数组（M是图像中的像素数量）。聚类完成后，我们将聚类中心值（同样是R、G、B值）应用到所有像素上，这样生成的图像将具有指定数量的颜色。最后，我们需要将数组重新调整回原始图像的形状。以下是代码实现：

python 复制代码 
import numpy as np
import cv2 as cv

img = cv.imread('home.jpg')
Z = img.reshape((-1,3))

# convert to np.float32
Z = np.float32(Z)

# define criteria, number of clusters(K) and apply kmeans()
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 8
ret,label,center=cv.kmeans(Z,K,None,criteria,10,cv.KMEANS_RANDOM_CENTERS)

# Now convert back into uint8, and make original image
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv.imshow('res2',res2)
cv.waitKey(0)
cv.destroyAllWindows()

查看 K=8 时的结果如下：

相关推荐
豆包MarsCode5 分钟前
倒计时 1 天｜TRAE SOLO 发布会日程抢先看
人工智能
WoShop商城源码24 分钟前
短视频矩阵系统：从源头到开发的全面解析
大数据·人工智能·其他·矩阵
许愿与你永世安宁35 分钟前
基于Llama的RAG 3种模型配置方法
人工智能·python·自然语言处理·json·github·llama·faiss
我有一计33341 分钟前
Qwen3-Embedding：原理解读和检索场景测试
人工智能·程序员
令狐寻欢44 分钟前
AI 大模型应用进阶系列（三）：大模型流式输出
人工智能·llm
AWS官方合作商1 小时前
深入解析 Amazon Q：AWS 推出的企业级生成式 AI 助手
人工智能·云计算·aws
聚客AI1 小时前
👉LLM的进化路线、领域微调及NLP的应用落地方式
人工智能·llm·掘金·日新计划
明心知1 小时前
DAY 18 推断聚类后簇的类型
人工智能·机器学习·聚类
墨城之左2 小时前
生命的底层逻辑
人工智能·程序人生
西猫雷婶2 小时前
python学智能算法（二十三）|SVM-几何距离
开发语言·人工智能·python·算法·机器学习·支持向量机
热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02Cursor Claude 模型无法使用的解决方法03KGG转MP3工具|非KGM文件|解密音频04【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致05集群聊天服务器---MySQL数据库的建立06【无标题】07Claude Code 最新版已经支持 Windows 安装使用！08身弱武修法：玄之又玄，奇妙之门09使用Ruby接入实时行情API教程102024电赛H题参考方案（+视频演示）——自动行使小车