2025年一区SCI-回旋镖气动椭圆优化算法Boomerang Aerodynamic Ellipse-附Matlab免费代码

引言

本期介绍一种新的元启发式算法------回旋镖气动椭圆优化算法Boomerang Aerodynamic Ellipse Optimizer (BAEO)。该优化器的灵感来自于飞行中的回旋镖的空气动力学行为，明确地建模了释放角和发射力如何塑造其轨迹。于2025年7月最新发表 在JCR 1区，中科院2区 SCI 期刊 Mathematics and Computers in Simulation。

回旋镖的飞行原理涉及空气动力学和陀螺仪效应。它的设计和形状允许它在飞行过程中产生旋转，并最终返回投掷者。因此，回飞镖的轨迹受作用力的角度和大小的影响，这两个因素共同决定了回飞镖在空中的路径和它返回的方式。就投掷角度而言，分为水平线和垂直线。抛回飞镖的水平角度直接影响回飞镖的水平飞行轨迹。通过描述回飞镖的运动特性和运动规律，建立了数学模型。由于回旋镖的空中轨迹直接取决于施加的发射力和释放角度，因此可以通过操纵这两个参数来操纵其在模拟中的飞行路径。在此前提下，一旦初始化了回旋镖椭圆气动优化器，就可以通过模拟连续的回旋镖投掷来探索可行解空间。

初始化：和其他群优化算法一样，采用随机初始化。

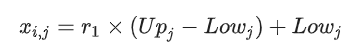
高回飞镖运动状态：

case 1：回旋镖基本状态，投掷时，只需要考虑投掷的角度、力度和方向等因素。由于此时的回飞镖不旋转，因此可以将此时的回飞镖抽象为粒子并建模。每扔一次回飞镖的力为：

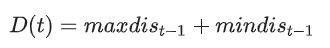
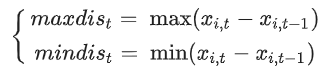
仍执回旋镖的方向：

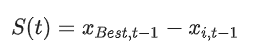
随着回旋镖投掷次数的增加，投掷力呈变化函数

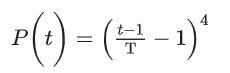
case2：回旋镖的空气旋转运动，当回力镖被抛出时，其在空中的运动状态为从抛出点到回弹点的弧线。在这种情况下，回旋镖的旋转可以看作是对可行域空间的全局搜索。回旋镖在空中旋转，数学表达式为

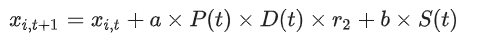
3.基于气动椭圆效应的均匀局部开发策略：通过对回旋镖在空中运动的分析，可以得出回旋镖的运动在周围空气中会产生气动效应的结论。在本文提出的策略中，当可行域为二维空间时，将具有该效应的区域近似视为椭球，并将该区域视为靠近解的局部搜索。为此，提出了一种对高维复杂目标函数具有可接受的时空复杂度和更好的搜索能力的新策略。

假设球体的圆心是原点，并且X，Y，Z都是相互独立且服从标准正态分布的随机变量，那么概率密度函数的分布点是:

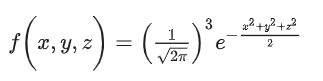
将均匀分布在球体上的随机点沿矢量直径方向投影到球体上，可以生成随机点。

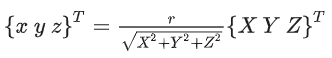
通过线性变换，将球面上的点映射到椭球上，并将椭球的三个半轴设为a,b,c.下面的线性变换将随机点从球体变换到椭球体；然而，这种变换可以近似为对球体的拉伸，并且点在椭球体上的分布并不均匀。此时，需要求解一个随机点的接受概率，使通过该概率接受的随机点在映射到椭球体时均匀分布，并证明映射点在椭球体上不是均匀分布的。

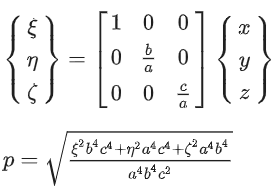
回旋镖运动的气动效应可以理解为在一个中心点产生一个椭球体，在这个椭球体上进行随机均匀点搜索。首先，以当前解的位置为中心，生成一系列符合正态分布的点集；然后，通过生成的点集到原点的距离和半轴的长度映射到高维椭球体。同时，将式进行高维扩展，得到下式：

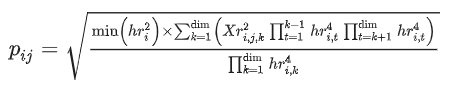
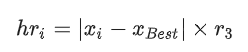
BAEO算法伪代码：

03. 对比验证

原文作者在对CEC2017基准函数的评估表明，所提出的BAEO优化器通过实现更低的适应度值和更快的收敛，同时在一系列问题维度上保持稳健的性能，从而始终优于最近的六种比较算法。在BSDS500数据集上的图像阈值分割应用表明，该算法具有较好的FSIM、SSIM和PSNR指标，在不同阈值计数下的分割质量稳定，验证了该算法在实际图像分割任务中的适应性和可靠性。

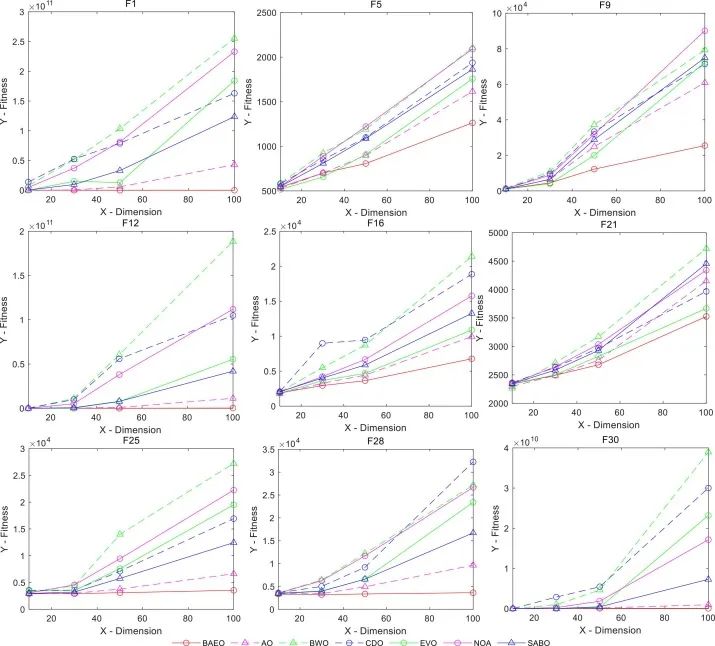
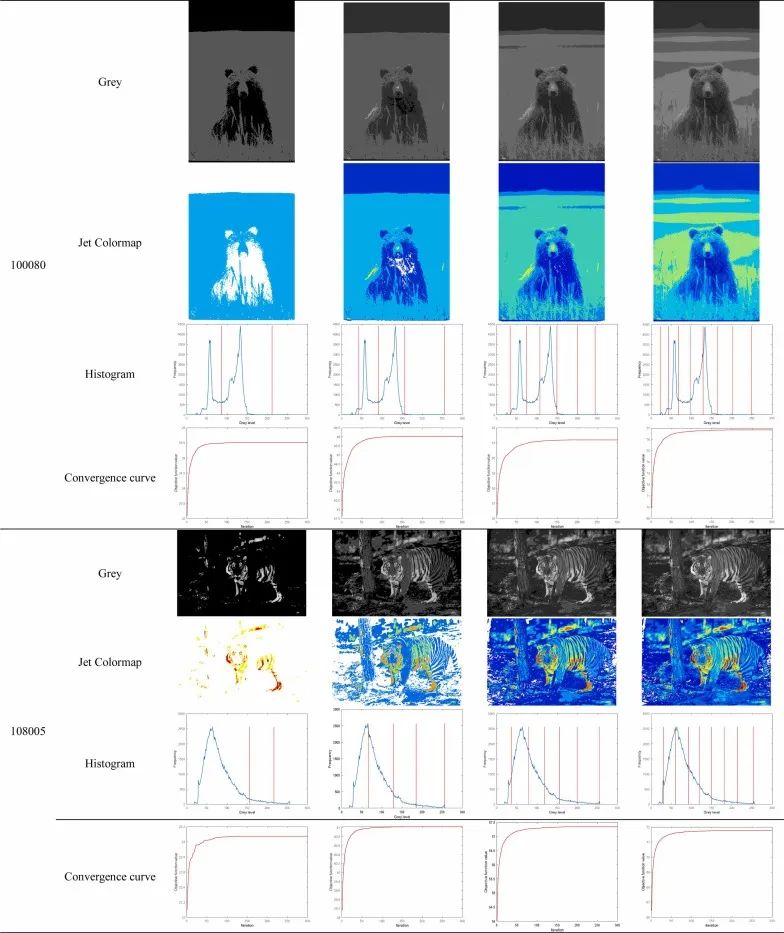
更多详细结果，请参阅相应的文献。

参考文献

Shijie Zhao, Fanshuai Meng, Liang Cai, Ronghua Yang,

Boomerang Aerodynamic Ellipse Optimizer: A human game-inspired optimization technique for numerical optimization and multilevel thresholding image segmentation,

Mathematics and Computers in Simulation,

2025,https://doi.org/10.1016/j.matcom.2025.07.006