一.前言
通过本章节学习了解LSTM内部结构及计算公式.,掌握Pytorch中LSTM⼯具的使⽤以及了解LSTM的优势与缺点.
二.LSTM介绍
LSTM(Long Short-Term Memory)也称⻓短时记忆结构, 它是传统RNN的变体, 与经典RNN相⽐能够有效 捕捉⻓序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时LSTM的结构更复杂, 它的核⼼结构可以分为四个部分去解析:
遗忘⻔
输⼊⻔
细胞状态
输出⻔
三.LSTM结构分析
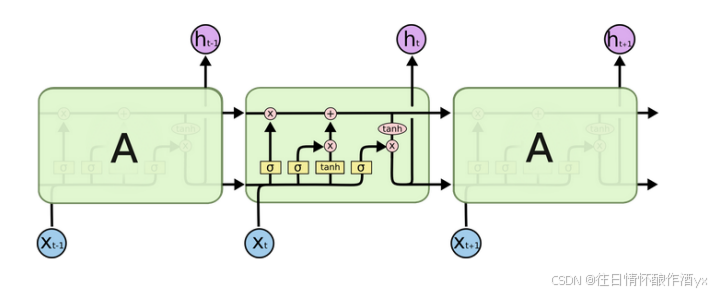
结构解释图:
遗忘⻔部分结构图与计算公式:
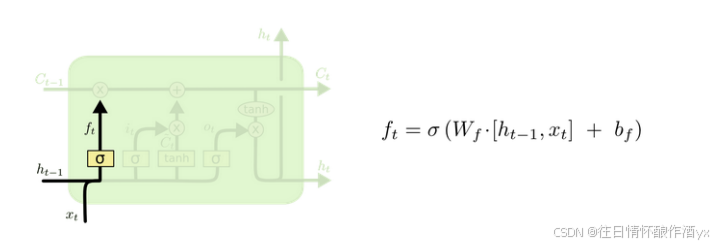
遗忘⻔结构分析:
与传统RNN的内部结构计算⾮常相似, ⾸先将当前时间步输⼊x(t)与上⼀个时间步隐含状态h(t-1) 拼接, 得到[x(t), h(t-1)], 然后通过⼀个全连接层做变换, 最后通过sigmoid函数进⾏激活得到f(t), 我 们可以将f(t)看作是⻔值, 好⽐⼀扇⻔开合的⼤⼩程度, ⻔值都将作⽤在通过该扇⻔的张量, 遗忘⻔ ⻔值将作⽤的上⼀层的细胞状态上, 代表遗忘过去的多少信息, ⼜因为遗忘⻔⻔值是由x(t), h(t-1)计 算得来的, 因此整个公式意味着根据当前时间步输⼊和上⼀个时间步隐含状态h(t-1)来决定遗忘多 少上⼀层的细胞状态所携带的过往信息.
遗忘⻔内部结构过程演示:
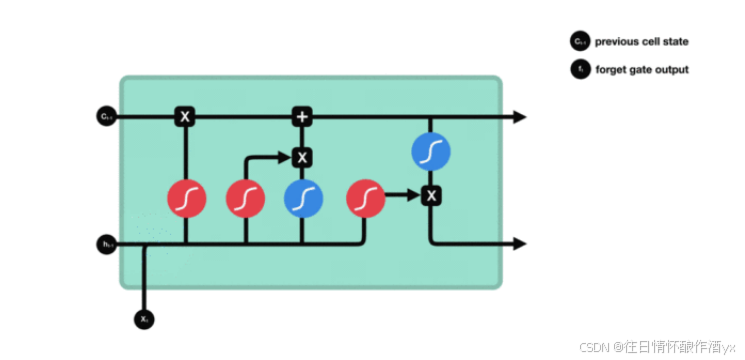
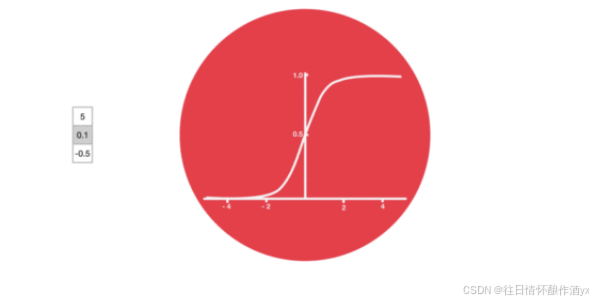
激活函数sigmiod的作⽤:
⽤于帮助调节流经⽹络的值, sigmoid函数将值压缩在0和1之间.
输⼊⻔部分结构图与计算公式:
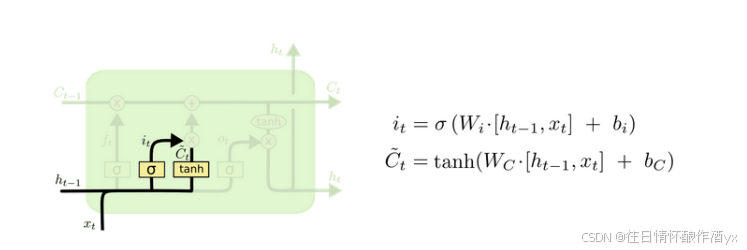
输⼊⻔结构分析:
我们看到输⼊⻔的计算公式有两个, 第⼀个就是产⽣输⼊⻔⻔值的公式, 它和遗忘⻔公式⼏乎相同, 区别只是在于它们之后要作⽤的⽬标上. 这个公式意味着输⼊信息有多少需要进⾏过滤. 输⼊⻔的 第⼆个公式是与传统RNN的内部结构计算相同. 对于LSTM来讲, 它得到的是当前的细胞状态, ⽽不 是像经典RNN⼀样得到的是隐含状态.
输⼊⻔内部结构过程演示:
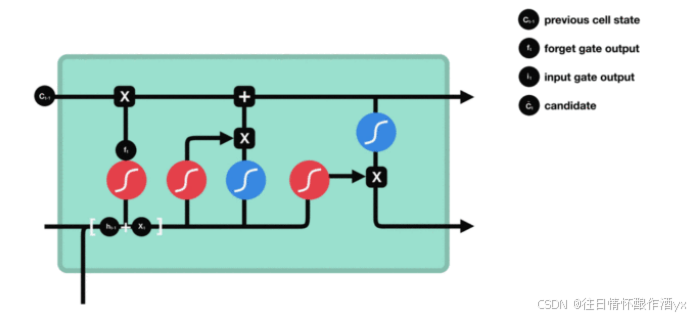
细胞状态更新图与计算公式:
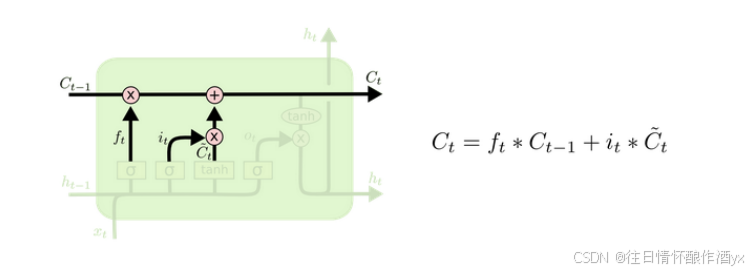
细胞状态更新分析:
细胞更新的结构与计算公式⾮常容易理解, 这⾥没有全连接层, 只是将刚刚得到的遗忘⻔⻔值与上 ⼀个时间步得到的C(t-1)相乘, 再加上输⼊⻔⻔值与当前时间步得到的未更新C(t)相乘的结果. 最终 得到更新后的C(t)作为下⼀个时间步输⼊的⼀部分. 整个细胞状态更新过程就是对遗忘⻔和输⼊⻔ 的应⽤.
细胞状态更新过程演示:
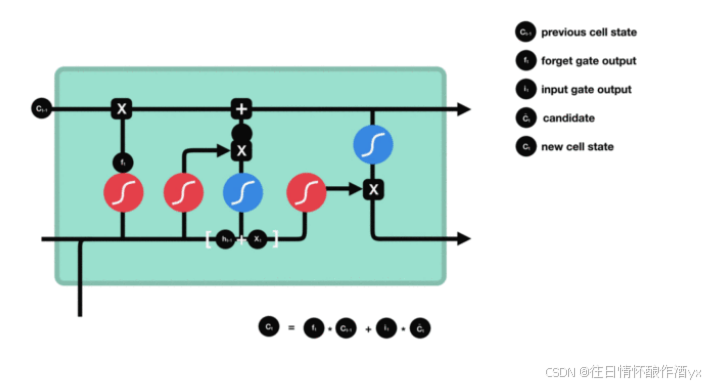
输出⻔部分结构图与计算公式:
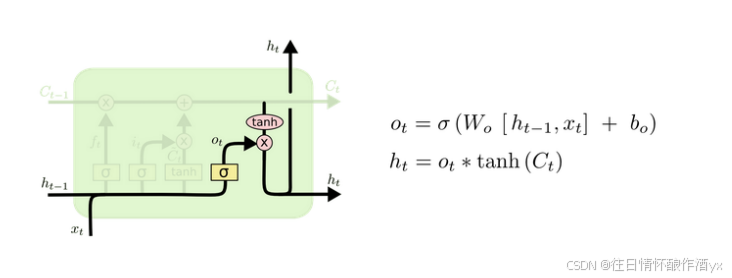
输出⻔结构分析:
输出⻔部分的公式也是两个, 第⼀个即是计算输出⻔的⻔值, 它和遗忘⻔,输⼊⻔计算⽅式相同. 第⼆个即是使⽤这个⻔值产⽣隐含状态h(t), 他将作⽤在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下⼀时间步输⼊的⼀部分. 整个输出⻔的过程, 就是为了产⽣隐含状态h(t).
输出⻔内部结构过程演示:
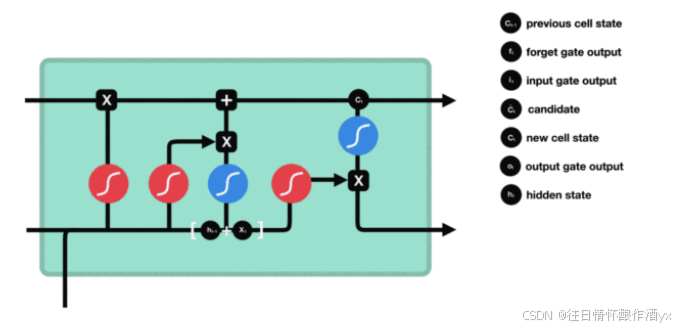
四.Bi-LSTM介绍
Bi-LSTM即双向LSTM, 它没有改变LSTM本身任何的内部结构, 只是将LSTM应⽤两次且⽅向不同, 再将两次得 到的LSTM结果进⾏拼接作为最终输出.
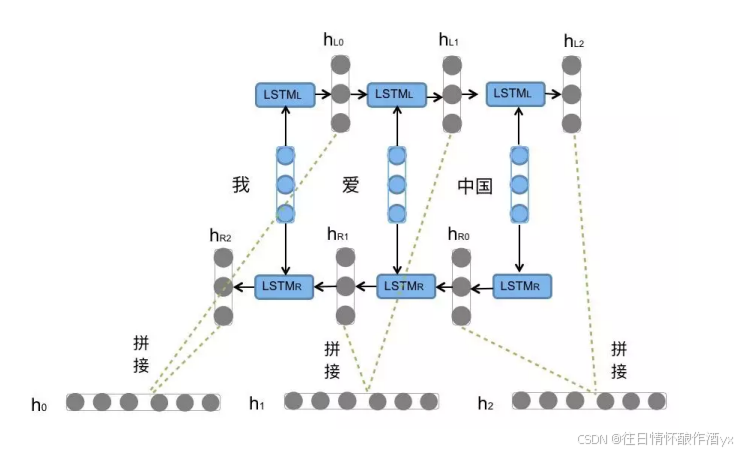
Bi-LSTM结构分析:
我们看到图中对"我爱中国"这句话或者叫这个输⼊序列, 进⾏了从左到右和从右到左两次LSTM处 理, 将得到的结果张量进⾏了拼接作为最终输出. 这种结构能够捕捉语⾔语法中⼀些特定的前置或 后置特征, 增强语义关联,但是模型参数和计算复杂度也随之增加了⼀倍, ⼀般需要对语料和计算资 源进⾏评估后决定是否使⽤该结构.
五.使用Pytorch构建LSTM模型
位置: 在torch.nn⼯具包之中, 通过torch.nn.LSTM可调⽤.
nn.LSTM类初始化主要参数解释:
input_size: 输⼊张量x中特征维度的⼤⼩.
hidden_size: 隐层张量h中特征维度的⼤⼩.
num_layers: 隐含层的数量.
bidirectional: 是否选择使⽤双向LSTM, 如果为True, 则使⽤; 默认不使⽤.
nn.LSTM类实例化对象主要参数解释:
input: 输⼊张量x.
h0: 初始化的隐层张量h.
c0: 初始化的细胞状态张量c.
nn.LSTM使⽤示例:
python
# 导入必要的库
import torch.nn as nn
import torch
# 定义一个LSTM网络
# 参数说明:
# 5: input_size - 输入特征的维度(每个时间步输入向量的长度)
# 6: hidden_size - 隐藏层特征的维度(LSTM输出的向量长度)
# 2: num_layers - LSTM的层数(堆叠的层数)
rnn = nn.LSTM(5, 6, 2)
# 定义输入张量
# 参数说明:
# 1: sequence_length - 序列长度(时间步数)
# 3: batch_size - 批次大小
# 5: input_size - 输入特征的维度
input = torch.randn(1, 3, 5)
# 定义初始隐藏状态
# 参数说明:
# 2: num_layers * num_directions(单向LSTM,所以num_directions=1)
# 3: batch_size
# 6: hidden_size
h0 = torch.randn(2, 3, 6)
# 定义初始细胞状态
# 形状和含义与h0相同
c0 = torch.randn(2, 3, 6)
# 前向传播计算
# 输入:input和初始状态(h0, c0)
# 输出:
# output: 所有时间步的输出 (seq_len, batch_size, hidden_size)
# hn: 最后一个时间步的隐藏状态 (num_layers, batch_size, hidden_size)
# cn: 最后一个时间步的细胞状态 (num_layers, batch_size, hidden_size)
output, (hn, cn) = rnn(input, (h0, c0))
# 打印输出结果
print("Output shape:", output.shape) # 预期输出形状:(1, 3, 6)
print(output) # 打印所有时间步的输出(本例中只有一个时间步)
print("\nFinal hidden state shape:", hn.shape) # 预期形状:(2, 3, 6)
print(hn) # 打印最终隐藏状态
print("\nFinal cell state shape:", cn.shape) # 预期形状:(2, 3, 6)
print(cn) # 打印最终细胞状态六.LSTM优缺点
LSTM优势:
LSTM的⻔结构能够有效减缓⻓序列问题中可能出现的梯度消失或爆炸, 虽然并不能杜绝这种现象, 但在 更⻓的序列问题上表现优于传统RNN
LSTM缺点:
由于内部结构相对较复杂, 因此训练效率在同等算⼒下较传统RNN低很多.
七.总结
本章节介绍了一下lstm的结构以及代码用法,期待大家的点赞关注加收藏