这篇论文主要研究了一种用于滑坡灾害时变概率评估的端到端混合深度学习模型------PCLA-Net。论文的核心内容和贡献包括:
-
问题背景
滑坡灾害具有显著的空间异质性和时间动态特征,传统数值模拟方法(如有限元法-极限平衡法)计算量大,难以实时预测和评估滑坡风险。
-
方法创新
提出了一个结合二维卷积神经网络(2D CNN)和长短期记忆网络(LSTM)以及注意力机制的混合深度学习框架------PCLA-Net。
- 2D CNN 用于提取滑坡区域的空间特征(如土壤参数的随机场)。
- LSTM 用于捕捉时间序列的动态变化(如降雨和水位波动)。
- 注意力机制帮助模型聚焦于关键的空间通道和时间节点,提高预测精度。
- 模型优势
- 能够端到端地从空间和时间数据联合学习,直接映射输入到安全系数和滑坡失稳概率预测。
- 相较于单独的 LSTM 或一维 CNN,PCLA-Net 在准确性和效率上表现更好。
- 需要的训练数据量大幅减少(至少降低50%),降低实际应用门槛。
-
案例验证
以中国重庆的liangshuijing滑坡为案例,通过与传统的有限元-极限平衡法(FEM-LEM)蒙特卡洛模拟对比,验证了PCLA-Net的准确性和泛化能力。
通过多种滑动窗口参数和注意力机制设置,系统地分析了模型性能及其影响因素。
-
应用前景
PCLA-Net非常适合实现数字孪生技术和在线学习的滑坡早期预警系统,可实现近实时的滑坡风险监测和动态更新,助力地质灾害风险管理。
-
未来方向
目前模型只能处理空间与时间非耦合数据,未来将研究改进模型结构以适应耦合时空数据,提升模型适用性和预测能力。
总结来说,这篇论文提出并验证了一个创新的深度学习模拟器,能高效准确地实现滑坡灾害的时变概率预测,具有重要的理论和工程应用价值。
作者:
Menglu Huang、Shin-ichi Nishimura、Toshifumi Shibata(日本冈山大学土木与环境工程系)
Ze Zhou Wang(通讯作者,玛丽·斯克沃多夫斯卡-居里学者,英国剑桥大学工程系)
作者单位:
a 冈山大学土木与环境工程系,日本冈山县北区津岛中 3-1-1,邮编 700-8530
b 玛丽·斯克沃多夫斯卡-居里学者,英国剑桥大学工程系,剑桥 CB3 0FA
1\] Huang M, Nishimura S ichi, Shibata T, et al. End-to-end time-dependent probabilistic assessment of landslide hazards using hybrid deep learning simulator\[J\]. Computers and Geotechnics, 2025, 178: 106920.
文章目录
-
-
- [1. 引言](#1. 引言)
- [2. 背景](#2. 背景)
-
- [2.1 随机场建模](#2.1 随机场建模)
- [2.2 瞬态渗流分析](#2.2 瞬态渗流分析)
- [2.3 卷积神经网络(CNN)](#2.3 卷积神经网络(CNN))
- [2.4 长短期记忆网络(LSTM)](#2.4 长短期记忆网络(LSTM))
- [3. PCLA-Net 模拟器](#3. PCLA-Net 模拟器)
-
- [3.1 整体架构](#3.1 整体架构)
- [3.2 注意力机制](#3.2 注意力机制)
- [3.2.1 混合通道--空间注意力机制](#3.2.1 混合通道–空间注意力机制)
- [3.2.2 时间注意力机制](#3.2.2 时间注意力机制)
- [4. 实现流程(Implementation procedures)](#4. 实现流程(Implementation procedures))
- [5. 案例研究(Case study)](#5. 案例研究(Case study))
-
- [5.1 工程背景描述(Project description)](#5.1 工程背景描述(Project description))
- [5.2 数值模拟(Numerical simulation)](#5.2 数值模拟(Numerical simulation))
- [5.3 PCLA-Net 模拟器的实现(PCLA-Net implementation)](#5.3 PCLA-Net 模拟器的实现(PCLA-Net implementation))
- [5.4 PCLA-Net 模拟器的验证](#5.4 PCLA-Net 模拟器的验证)
- [5.5 注意力机制的影响](#5.5 注意力机制的影响)
- [5.6. 预测时间跨度(Forecast Horizon, FH)的影响](#5.6. 预测时间跨度(Forecast Horizon, FH)的影响)
- [6. 与其他技术的对比](#6. 与其他技术的对比)
- [7. 结论](#7. 结论)
-
摘要:
滑坡灾害的预警检测通常需要实时或近实时的预测,但这在存在多种地质不确定性和时间变化的外部环境载荷的情况下极具挑战性。在系统层面上传播这些不确定性以理解边坡的时空行为,往往需要耗时的数值计算,严重制约了预警系统的建立。本文提出了一种混合深度学习模拟器,融合了并行卷积神经网络(CNN)和长短期记忆网络(LSTM),并通过注意力机制进行连接,称为 PCLA-Net,以实现滑坡灾害的时间依赖概率评估。
PCLA-Net 具有两个创新点。首先,它能够同时处理时间信息和空间信息。CNN 擅长解析空间数据,而 LSTM 擅长处理时间变化数据。结合两种注意力机制,这两个模块被整合用于对边坡的时空行为进行概率预测。其次,PCLA-Net 实现了端到端的预测。在本文中,选取中国三峡库区的Liangshuijing滑坡作为案例来展示 PCLA-Net 的应用。模型首先通过验证实验进行评估,并与现有技术进行比较,以展示其预测能力的提升。结果表明,所提出的 PCLA-Net 模拟器在保持相同预测精度的同时,可实现至少 50% 的计算资源节约。
关键词: 空间变异性;时间依赖可靠性;卷积神经网络;长短期记忆网络;注意力机制;滑坡灾害
1. 引言
滑坡是全球最常见且破坏性极大的地质灾害之一,对人类生命、财产及基础设施系统构成严重威胁(Tang 等,2019;Zhang 等,2024)。准确评估边坡稳定性是岩土工程长期以来的核心任务,对于滑坡灾害的预测与影响理解至关重要。用于预测边坡稳定性的技术不断演进,从 Taylor 的边坡稳定图表(Taylor,1937;Steward 等,2011)、Bishop 法(Bishop,1955)到 Morgenstern-Price(M-P)法(Morgenstern 和 Price,1965)以及数值模拟方法等,这些方法在工程实践中被广泛采用。它们通常假设土体为均质介质,并通过安全系数(Fs)来量化边坡的稳定性。
然而,由于土体参数存在固有及空间变异性(Phoon 和 Kulhawy,1999;Griffiths 和 Fenton,2004;Jiang 等,2014),基于均质假设并仅使用单一安全系数(Fs)进行边坡稳定性评估已难以满足严谨性的要求。因此,越来越多的研究采用概率性评估方法,以考虑边坡系统中存在的多种不确定性,常用的量化指标包括 Fs 的均值与标准差、失效概率(Pf)或可靠指标。
为满足边坡系统的概率性评估需求,各种方法被广泛应用。虽然蒙特卡洛模拟(MCS)被认为是最通用的不确定性传播方法,但其计算效率常受到质疑。因此,提出了多种方差缩减策略,如子集模拟(SS)(Au 和 Beck,2001)、重要性采样(IS)(Tabandeh 等,2022)、线性采样(LS)(Pradlwarter 等,2007)以及方向采样(DS)(Melchers,1994),这些方法已在边坡概率稳定性分析中得到广泛应用。例如,Huang 等(2021)利用贝叶斯方法对土体参数的条件随机场进行了校准,并采用 SS 方法对中国三峡库区在极端降雨条件下的石柳树包滑坡进行了概率分析。
然而,这些随机计算方法仍需大量重复模拟,导致计算代价高昂,尤其在时间依赖的可靠性分析中,每一个时间步都需进行概率计算,进一步增加了计算负担。这一限制显著制约了滑坡灾害的实时或近实时预警可行性。为提升计算效率,研究中还广泛采用了近似方法,如一阶可靠性方法(FORM)(Hu 等,2023)与二阶可靠性方法(SORM)(Raghuram 和 Basha,2023),但它们在处理高度非线性系统和高维不确定性信息方面存在挑战,同时其计算精度对初始设计点的选择高度敏感。类似地,基于概率守恒的演化方法(如概率密度演化方法)(Li,2016;Pang 等,2021)虽具有坚实的理论基础,但在处理高维不确定性或极低失效概率事件时也面临数值困难。
为克服上述问题,替代模型(surrogate model)技术被越来越多地采用。替代模型可在大幅降低计算成本的前提下,逼近高开销模拟的系统行为。因此,它们常与 MCS、SS、IS、LS、DS 等计算方法结合使用,以高效完成概率性评估。目前应用于岩土系统概率评估的替代模型包括:多项式混沌展开(Jiang 和 Huang,2016;Guo 等,2018)、高斯过程回归(Kang 等,2015;Echard 等,2011)、支持向量机(Xu 等,2023)、集成学习方法(Wang 等,2020;Zhang 等,2022;Li 等,2022)以及深度学习方法(Wang 和 Goh,2021;Wang,2022;Soranzo 等,2023;Jiang 等,2023;Wang 等,2024b)。
替代模型成功应用的关键在于其逼近精度。然而,岩土系统中常涉及多个不确定性来源,如土体性质的高维空间变异性及环境荷载的时变性,这使得部分替代模型难以在高度不确定性条件下准确模拟系统行为。在此背景下,基于深度学习的替代模型展现出更大的潜力。
此外,由于外部环境荷载存在时间变化性,边坡稳定性也表现出明显的时间依赖性。因此,开展时间依赖的概率性评估对于滑坡的及时预警与减灾尤为关键。但这种类型的分析需在多个时间步上进行概率计算,不仅显著增加总体计算量,也使构建高精度替代模型更具挑战,尤其是在需同时考虑土体参数的高维空间变异性时。
已有研究尝试解决这一问题。例如,Guardiani 等(2022)在一个快速降水情境下的假设边坡中采用极端梯度提升(XGBoost)作为替代模型进行时间依赖概率评估,但该方法需对每个时间步分别构建模型,无法预测未来时间步的边坡可靠性。随后,Zhang 等(2023)结合 XGBoost 与 LightGBM,对三峡库区巴子门滑坡进行了时间依赖概率评估,输入参数包括有效黏聚力( c ′ c' c′)、有效内摩擦角( ϕ ′ \phi' ϕ′)、饱和渗透系数( k _ s k\_s k_s)以及时间变化的降雨与水位数据。虽然模型将整个时间序列的环境荷载作为输入,构建了所谓的"全局模型",但忽略了土体参数的空间变异性,这种简化常被批评为导致失效概率( P _ f P\_f P_f)的评估过于保守或不现实(Jiang 等,2020a)。
为此,Wang 等(2023)与 Wang 等(2024a)提出了一种考虑土体空间变异性的滑坡时间依赖概率评估框架。然而,其使用的替代模型仍是在 P _ f P\_f P_f 空间中构建的,即通过集成学习或深度学习模型拟合时间变化环境荷载与 P _ f P\_f P_f 值之间的关系。该实现方式存在一项显著限制:必须先通过蒙特卡洛模拟结合原始数值模型,在系统层面传播土体空间变异性,以获得每个时间步的 P _ f P\_f P_f,从而用以构建替代模型,这会引发巨大的计算成本。因此,该框架尚不能实现真正意义上的端到端建模,因为土体参数的空间变异性并未直接融入替代建模过程。
基于上述背景,本文提出了一种新型混合深度学习模拟器,命名为 PCLA-Net ,用于实现考虑土体空间变异性与环境荷载时变性的滑坡灾害端到端时间依赖概率评估。该模拟器结合了卷积神经网络(CNN)与长短期记忆网络(LSTM),并引入了通道-空间注意力机制与时间注意力机制。CNN 擅长处理如土体空间变异性等空间数据,LSTM 则擅长建模时变信息。这两种注意力机制的设计,使两个模块能够协同预测滑坡的时空演化行为。
与已有深度学习方法(Guardiani 等,2022;Zhang 等,2023;Wang 等,2023;Wang 等,2024a)相比,PCLA-Net 的贡献主要体现在以下两个方面:
- 真正的全局模型 :该模型将所有时间步的空间与时间数据整合至单一替代模型中,并具备预测未来时间步的能力;
- 端到端建模能力 :模型可同时直接处理高维随机场(土体空间变异性)与时间变化环境荷载,在每个时间步输出概率性结果。
这两项特性共同简化了实现流程,显著减少了重复模拟次数,避免了为每个时间步分别构建替代模型的繁琐工作。多类型数据的同时考虑还支持了对滑坡时空动态更全面的概率性评估。
2. 背景
2.1 随机场建模
随机场被广泛用于模拟土体性质的固有空间变异性。随机场的生成通常依赖于自相关函数,该函数量化了在特定距离下两个空间点之间的空间相关性。典型的二维(2D)高斯随机场可基于以下参数进行模拟:(i) 均值;(ii) 变异系数(CoV);以及 (iii) 波动尺度。
在本研究中,采用高斯自相关函数并结合 Karhunen--Loève(K--L)展开技术对随机场进行离散化。一个二维对数正态随机场的 realizations H ( x , y ) H(x, y) H(x,y) 可通过 K--L 展开技术获得(Phoon et al., 2002;Jiang et al., 2014),表示如下:
H ( x , y ) = exp [ μ ln + σ ln ∑ i = 1 M λ i f i ( x , y ) ξ i ] = exp [ μ ln + σ ln H G ( x , y ) ] (1) H(x, y) = \exp\left[ \mu_{\ln} + \sigma_{\ln} \sum_{i=1}^{M} \sqrt{\lambda_i} f_i(x, y)\xi_i \right] = \exp\left[\mu_{\ln} + \sigma_{\ln} H_G(x, y) \right] \tag{1} H(x,y)=exp[μln+σlni=1∑Mλi fi(x,y)ξi]=exp[μln+σlnHG(x,y)](1)
其中, ( x , y ) (x, y) (x,y) 表示随机场离散网格中高斯积分点的坐标。 μ ln = ln μ − 0.5 σ ln 2 \mu{\ln} = \ln \mu - 0.5 \sigma_{\ln}^2 μln=lnμ−0.5σln2, σ _ ln = ln ( 1 + C o V 2 ) \sigma\_{\ln} = \sqrt{\ln(1 + \mathrm{CoV}^2)} σ_ln=ln(1+CoV2) 分别为对数正态随机场的均值和标准差, μ \mu μ 是高斯随机场的均值。 λ _ i \lambda\_i λ_i 和 f _ i ( x , y ) f\_i(x, y) f_i(x,y) 分别表示二维自相关函数的特征值与特征向量, ξ _ i \xi\_i ξ_i 为独立标准正态随机变量。 M M M 表示级数展开的项数, H _ G ( x , y ) H\_G(x, y) H_G(x,y) 为具有 M M M 项的标准正态分布随机场。
公式 (1) 仅适用于单一土体参数的随机场生成。当需要同时考虑多个土体参数的随机场时,必须考虑参数之间的交叉相关性(Guo et al., 2019;Jiang et al., 2020b)。以 c ′ c' c′ 和 ϕ ′ \phi' ϕ′ 为例,交叉相关的对数正态随机场可表示为:
H c ′ ( x , y ) = exp [ μ ln c ′ + σ ln c ′ H G c ′ ( x , y ) ] (2-1) H_{c'}(x, y) = \exp\left[\mu_{\ln c'} + \sigma_{\ln c'} H_{G}^{c'}(x, y) \right] \tag{2-1} Hc′(x,y)=exp[μlnc′+σlnc′HGc′(x,y)](2-1)
H ϕ ′ ( x , y ) = exp { μ ln ϕ ′ + σ ln ϕ ′ [ H G c ′ ( x , y ) ρ ln c ′ , ln ϕ ′ + H G ϕ ′ ( x , y ) 1 − ρ ln c ′ , ln ϕ ′ 2 ] } (2-2) H_{\phi'}(x, y) = \exp\left\{ \mu_{\ln \phi'} + \sigma_{\ln \phi'} \left[ H_{G}^{c'}(x, y) \rho_{\ln c', \ln \phi'} + H_{G}^{\phi'}(x, y) \sqrt{1 - \rho_{\ln c', \ln \phi'}^2} \right] \right\} \tag{2-2} Hϕ′(x,y)=exp{μlnϕ′+σlnϕ′[HGc′(x,y)ρlnc′,lnϕ′+HGϕ′(x,y)1−ρlnc′,lnϕ′2 ]}(2-2)
其中, ρ _ ln c ′ , ln ϕ ′ \rho\_{\ln c', \ln \phi'} ρ_lnc′,lnϕ′ 表示 ln c ′ \ln c' lnc′ 与 ln ϕ ′ \ln \phi' lnϕ′ 之间的交叉相关系数。
2.2 瞬态渗流分析
在非饱和土中进行瞬态渗流分析的第一步是基于饱和导水率 k _ s k\_s k_s 计算非饱和土的导水率 k k k,依据 Schaap 和 Leij(2000)的方法如下:
k = k s S e [ 1 − ( 1 − S e 1 / m ) m ] 2 (3) k = k_s S_e^{[1 - (1 - S_e^{1/m})^m]^2} \tag{3} k=ksSe[1−(1−Se1/m)m]2(3)
其中, S _ e S\_e S_e 为有效饱和度, m m m 为正值拟合参数。上述两个参数由 Van Genuchten 模型(VGM)(Van Genuchten, 1980)给出如下关系:
S e = θ w − θ r θ s − θ r = [ 1 + ( ψ α ) n ] − m (4) S_e = \frac{\theta_w - \theta_r}{\theta_s - \theta_r} = \left[1 + \left(\frac{\psi}{\alpha}\right)^n \right]^{-m} \tag{4} Se=θs−θrθw−θr=[1+(αψ)n]−m(4)
其中, θ _ s \theta\_s θ_s 与 θ _ r \theta\_r θ_r 分别表示饱和与残余体积含水量, α \alpha α、 m m m 与 n n n(其中 m = 1 − 1 / n m = 1 - 1/n m=1−1/n)为正值曲线拟合参数。Van Genuchten 模型是导出土--水特征曲线(SWCC)的广泛应用方法,SWCC 描述了体积含水率 θ \theta θ 与基质吸力 ψ \psi ψ 之间的关系。
最后,Richards(1931)提出了非饱和土二维瞬态渗流的控制方程,如下所示:
∂ ∂ x ( k x ∂ h ∂ x ) + ∂ ∂ y ( k y ∂ h ∂ y ) + Q = ∂ θ ∂ t (5) \frac{\partial}{\partial x} \left( k_x \frac{\partial h}{\partial x} \right) + \frac{\partial}{\partial y} \left( k_y \frac{\partial h}{\partial y} \right) + Q = \frac{\partial \theta}{\partial t} \tag{5} ∂x∂(kx∂x∂h)+∂y∂(ky∂y∂h)+Q=∂t∂θ(5)
其中, k _ x k\_x k_x 与 k _ y k\_y k_y 分别为水平方向与垂直方向的导水率, h h h 表示总水头, Q Q Q 为施加的边界通量。在本研究中,采用有限元法对上述控制方程进行求解,渗流分析结果将用于后续的极限平衡分析,相关信息将在后文中详细阐述。
2.3 卷积神经网络(CNN)
卷积神经网络(CNN)是一类强大的深度学习模型,在多个领域中取得了显著成果(LeCun 等, 1998;Krizhevsky 等, 2012)。根据输入数据维度的不同,CNN 可分为两类:二维 CNN(2D CNN)用于处理类似图像的网格结构数据;一维 CNN(1D CNN)适用于处理时间序列或信号等序列数据。
CNN 的设计灵感来自人类视觉系统,能通过多层卷积、池化与全连接层自动学习输入数据的层级表示。其中,卷积层作为特征提取器,通过可学习的卷积核(又称滤波器)提取输入数据的局部模式和空间依赖性。这些滤波器在输入上滑动,对局部区域执行元素乘积和求和操作,生成特征图。随后,池化层对特征图进行下采样,降低空间维度,同时保留最显著的信息,从而引入平移不变性并降低计算复杂度。
CNN 的架构使其能有效捕捉并利用岩土数据中固有的空间结构。通过参数共享与局部连接机制,CNN 可学习具有平移不变性的特征,对输入数据的微小变化具有鲁棒性。
2.4 长短期记忆网络(LSTM)
长短期记忆网络(LSTM)是一种特殊的循环神经网络(RNN)架构,采用门控机制以捕捉长期依赖关系,有效缓解传统 RNN 中常见的梯度消失或爆炸问题。凭借这一特性,LSTM 能够从复杂时间序列中提取精细模式并捕捉长距离依赖关系(Hochreiter 和 Schmidhuber, 1997;Gers 等, 2000)。
如图 1 所示,LSTM 单元的核心组件包括输入门( i _ t i\_t i_t)、遗忘门( f _ t f\_t f_t)和输出门( o _ t o\_t o_t),各自承担不同功能。输入门控制哪些信息可以进入记忆单元;遗忘门决定当前时刻应丢弃哪些信息;输出门则控制哪些信息从记忆单元传递至下一隐藏状态。
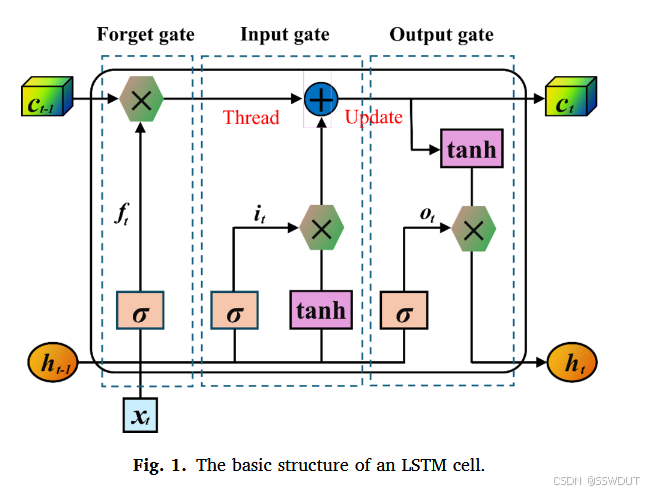
这些门控机制协同工作,使得 LSTM 在长短期时间序列预测任务中优于传统 RNN。各门控的计算过程如下:
i t = σ ( W x i x t + W h i h t − 1 + W c i ⊙ c t − 1 + b i ) (6) i_t = \sigma(W_{xi} x_t + W_{hi} h_{t-1} + W_{ci} \odot c_{t-1} + b_i) \tag{6} it=σ(Wxixt+Whiht−1+Wci⊙ct−1+bi)(6)
f t = σ ( W x f x t + W h f h t − 1 + W c f ⊙ c t − 1 + b f ) (7) f_t = \sigma(W_{xf} x_t + W_{hf} h_{t-1} + W_{cf} \odot c_{t-1} + b_f) \tag{7} ft=σ(Wxfxt+Whfht−1+Wcf⊙ct−1+bf)(7)
o t = σ ( W x o x t + W h o h t − 1 + W c o ⊙ c t + b o ) (8) o_t = \sigma(W_{xo} x_t + W_{ho} h_{t-1} + W_{co} \odot c_t + b_o) \tag{8} ot=σ(Wxoxt+Whoht−1+Wco⊙ct+bo)(8)
c t = f t ⊙ c t − 1 + i t ⊙ tanh ( W x c x t + W h c h t − 1 + b c ) (9) c_t = f_t \odot c_{t-1} + i_t \odot \tanh(W_{xc} x_t + W_{hc} h_{t-1} + b_c) \tag{9} ct=ft⊙ct−1+it⊙tanh(Wxcxt+Whcht−1+bc)(9)
h t = o t ⊙ tanh ( c t ) (10) h_t = o_t \odot \tanh(c_t) \tag{10} ht=ot⊙tanh(ct)(10)
其中, x _ t x\t x_t 为当前时间步的输入; W _ ∗ W\* W_∗ 和 b _ ∗ b\* b∗ 分别表示权重矩阵与偏置; σ ( ⋅ ) \sigma(\cdot) σ(⋅) 为 sigmoid 激活函数, tanh ( ⋅ ) \tanh(\cdot) tanh(⋅) 为双曲正切函数; ⊙ \odot ⊙ 表示 Hadamard(逐元素)乘积。
公式 (6)-(8) 描述了当前时间步 t t t 中输入门、遗忘门与输出门的计算过程,公式 (9)-(10) 描述了记忆单元 c _ t c\_t c_t 和隐藏状态 h _ t h\_t h_t 的更新过程。
3. PCLA-Net 模拟器
3.1 整体架构
图 2 展示了所提出的端到端混合深度学习模拟器的总体结构,该模拟器用于实现滑坡灾害的时变概率评估。该模拟器称为 PCLA-Net ,它融合了并行卷积神经网络(CNN)与带注意力机制的长短期记忆网络(LSTM)。通过使用 2D CNN 进行空间特征提取、LSTM 网络进行时间特征提取,PCLA-Net 能够有效捕捉来自非耦合空间与时间数据的高度非线性特征。
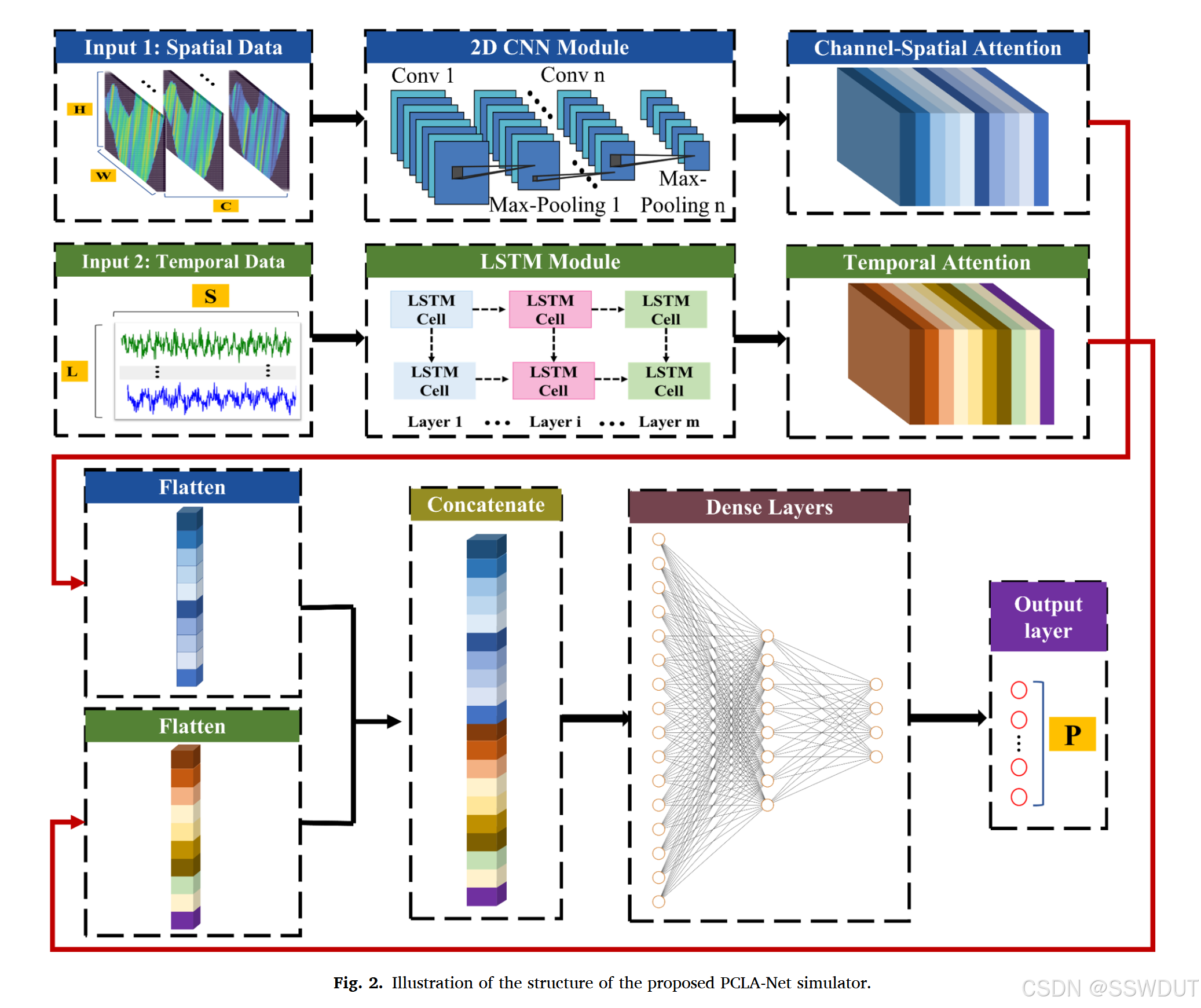
如图 2 所示,PCLA-Net 利用 2D CNN 对输入 1 中的空间特征进行编码,同时通过输入 2 中的时变外部荷载数据动态更新 LSTM 的隐藏状态,从而捕捉其时间动态特征。该设计使模型能够高效处理静态空间信息,并将其与学习到的时间依赖关系相融合。
随后,提取的局部空间与时间特征通过混合通道--空间注意力机制与时间注意力机制进行进一步优化。这两个注意力机制的具体细节将在下节中介绍。随后,全连接层将这些优化后的局部特征转换为全局表示,最后一个回归输出层将全局特征映射到序列形式的安全系数( F _ s F\_s F_s)数据,从而实现 PCLA-Net 模拟器对空间与时间数据的同步学习与高精度预测。
PCLA-Net 模拟器的结构支持端到端实现,能快速响应实时变化,对于实现数字孪生、预警系统以及地质系统的持续监测和更新具有关键意义。
3.2 注意力机制
注意力机制在增强特征表示能力方面发挥着至关重要的作用,其核心思想是强化最相关的信息。在复杂的时空数据背景下,不同的通道、空间位置和时间点的重要性可能大不相同。
为有效捕捉这种重要性的差异性,PCLA-Net 采用了 混合通道--空间注意力机制 和 时间注意力机制 来同时优化空间与时间特征。混合通道--空间注意力机制使模型能够关注每个时间步中最具信息量的通道和空间位置;时间注意力机制则使模型能够对不同时间步赋予不同权重,从而捕捉长期依赖关系并聚焦关键时间信息。
这两个机制共同增强了模型的预测能力,使其能够动态地聚焦输入数据中最关键的部分,类似于人类专家在分析复杂数据时优先关注关键信息的方式。这种方法显著提高了模型对滑坡灾害评估所涉大量空间与时间数据的处理和理解能力,进而实现更准确、更可靠的预测。
3.2.1 混合通道--空间注意力机制
该机制结合了通道注意力(Channel Attention, CA)与空间注意力(Spatial Attention, SA)来增强特征表示能力。如图 3 所示,该机制包含两个主要阶段。
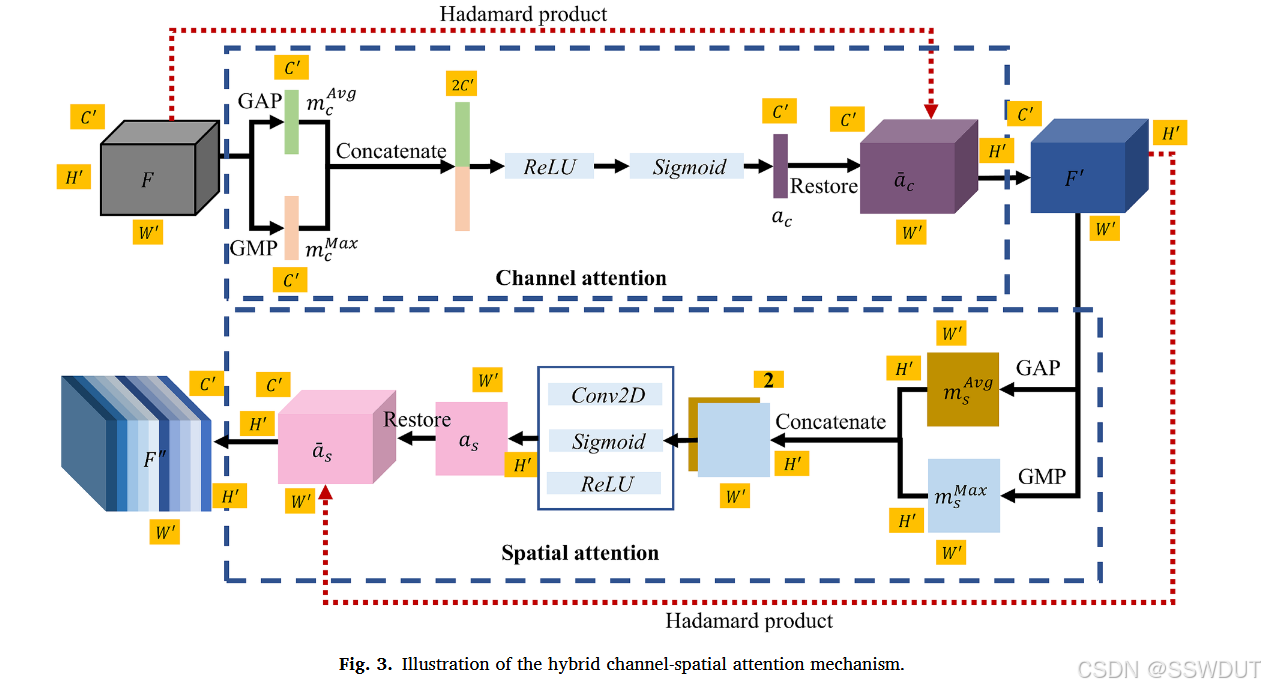
首先,通道注意力通过对来自 2D CNN 模块的特征图 F ∈ R W ′ × H ′ × C ′ F \in \mathbb{R}^{W' \times H' \times C'} F∈RW′×H′×C′ 进行空间维度上的全局平均池化(GAP)和全局最大池化(GMP),分别得到两个向量 m c _ Avg ( F ) ∈ R C ′ mc\{\text{Avg}}(F) \in \mathbb{R}^{C'} mc_Avg(F)∈RC′ 和 m c _ Max ( F ) ∈ R C ′ mc\{\text{Max}}(F) \in \mathbb{R}^{C'} mc_Max(F)∈RC′。这两个向量被拼接为一个维度为 2 C ′ 2C' 2C′ 的特征向量,并输入到一个共享的两层感知机中。
第一层通过 ReLU 激活函数将特征维度从 2 C ′ 2C' 2C′ 降至 C ′ / r C'/r C′/r,其中 r r r 为压缩比;第二层使用 Sigmoid 激活函数将特征维度恢复至 C ′ C' C′,从而生成通道注意力权重图 a _ c ∈ R C ′ a\_c \in \mathbb{R}^{C'} a_c∈RC′。
例如,若输入特征图有 256 个通道,且压缩比 r = 2 r = 2 r=2,则池化后的拼接向量为 512 维;第一层降维至 128,第二层再升维至 256,对应原始输入通道数。这使得网络能学习通道间的依赖关系,并自适应地调整通道响应。
a c = σ ( w 2 ⋅ ReLU ( w 1 ⋅ [ m c Avg ( F ) , m c Max ( F ) ] + b 1 ) + b 2 ) (11) a_c = \sigma\left(w_2 \cdot \text{ReLU}\left(w_1 \cdot [mc_{\text{Avg}}(F), mc_{\text{Max}}(F)] + b_1\right) + b_2\right) \tag{11} ac=σ(w2⋅ReLU(w1⋅[mcAvg(F),mcMax(F)]+b1)+b2)(11)
其中, w _ 1 , w _ 2 w\_1, w\_2 w_1,w_2 为可学习的权重, b _ 1 , b _ 2 b\_1, b\_2 b_1,b_2 为偏置项。这些参数在训练初始时被随机初始化,并通过最小化损失函数进行优化。
接下来,将 a _ c a\_c a_c 恢复为与 F F F 相同的维度,并进行逐元素乘法运算(Hadamard 乘积)以获得通道优化后的特征图 F ′ ∈ R W ′ × H ′ × C ′ F' \in \mathbb{R}^{W' \times H' \times C'} F′∈RW′×H′×C′:
F ′ = a c ⊙ F (12) F' = a_c \odot F \tag{12} F′=ac⊙F(12)
然后,应用空间注意力机制对 F ′ F' F′ 进一步处理。首先在通道维度上进行平均池化与最大池化,得到 m s _ Avg ( F ′ ) ∈ R W ′ × H ′ ms\{\text{Avg}}(F') \in \mathbb{R}^{W' \times H'} ms_Avg(F′)∈RW′×H′ 与 m s _ Max ( F ′ ) ∈ R W ′ × H ′ ms\{\text{Max}}(F') \in \mathbb{R}^{W' \times H'} ms_Max(F′)∈RW′×H′。这两个特征图沿通道维度拼接后送入一个卷积层以聚合空间信息。
该卷积层采用大小为 ( 5 , 5 ) (5, 5) (5,5) 的核,步幅为 1,并使用"same"填充策略以保持输出与输入的空间维度一致。卷积结果再经过一个两层感知机,其中第一层使用 ReLU,第二层使用 Sigmoid,最终生成空间注意力权重图 a _ s ∈ R W ′ × H ′ a\_s \in \mathbb{R}^{W' \times H'} a_s∈RW′×H′:
a s = σ ( w 4 ⋅ ReLU ( w 3 ⋅ Conv ( [ m s Avg ( F ′ ) , m s Max ( F ′ ) ] ) + b 3 ) + b 4 ) (13) a_s = \sigma\left(w_4 \cdot \text{ReLU}\left(w_3 \cdot \text{Conv}([ms_{\text{Avg}}(F'), ms_{\text{Max}}(F')]) + b_3\right) + b_4\right) \tag{13} as=σ(w4⋅ReLU(w3⋅Conv([msAvg(F′),msMax(F′)])+b3)+b4)(13)
最后,将 a _ s a\_s a_s 扩展至与 F ′ F' F′ 相同维度,并与 F ′ F' F′ 进行逐元素乘法,得到最终优化后的特征图 F ′ ′ F'' F′′:
F ′ ′ = a s ⊙ F ′ (14) F'' = a_s \odot F' \tag{14} F′′=as⊙F′(14)
3.2.2 时间注意力机制
时间注意力机制用于优化由 LSTM 模块提取的时间特征 h ∈ R S × D h \in \mathbb{R}^{S \times D} h∈RS×D,其中 S S S 表示时间窗口大小, D D D 表示隐藏状态维度,通常等于 LSTM 最后一层单元数。
该机制首先计算不同时间步 i i i 和 j j j 的隐藏状态 h _ i ∈ R D h\_i \in \mathbb{R}^D h_i∈RD 与 h _ j ∈ R D h\j \in \mathbb{R}^D h_j∈RD 之间的相似度 a _ i j a\{ij} a_ij,计算方式如下:
a i j = tanh ( w 5 h i + w 6 h j + b 5 ) (15) a_{ij} = \tanh(w_5 h_i + w_6 h_j + b_5) \tag{15} aij=tanh(w5hi+w6hj+b5)(15)
得到的相似度矩阵 a ∈ R S × S a \in \mathbb{R}^{S \times S} a∈RS×S 再通过 Softmax 函数进行归一化,获得时间注意力权重图 b ∈ R S × S b \in \mathbb{R}^{S \times S} b∈RS×S:
b i j = exp ( a i j ) ∑ j = 1 S exp ( a i j ) (16) b_{ij} = \frac{\exp(a_{ij})}{\sum_{j=1}^{S} \exp(a_{ij})} \tag{16} bij=∑j=1Sexp(aij)exp(aij)(16)
最后,使用加权求和方式对每个时间步 i i i 的隐藏状态进行优化,得到优化后的时间特征 h ′ _ i h'\_i h′_i:
h i ′ = ∑ j = 1 S b i j h j (17) h'i = \sum{j=1}^{S} b_{ij} h_j \tag{17} hi′=j=1∑Sbijhj(17)
4. 实现流程(Implementation procedures)
本节解释了所提出的 PCLA-Net 模拟器的实现框架中的一些关键步骤。如图 4 所示,整体实现步骤如下:
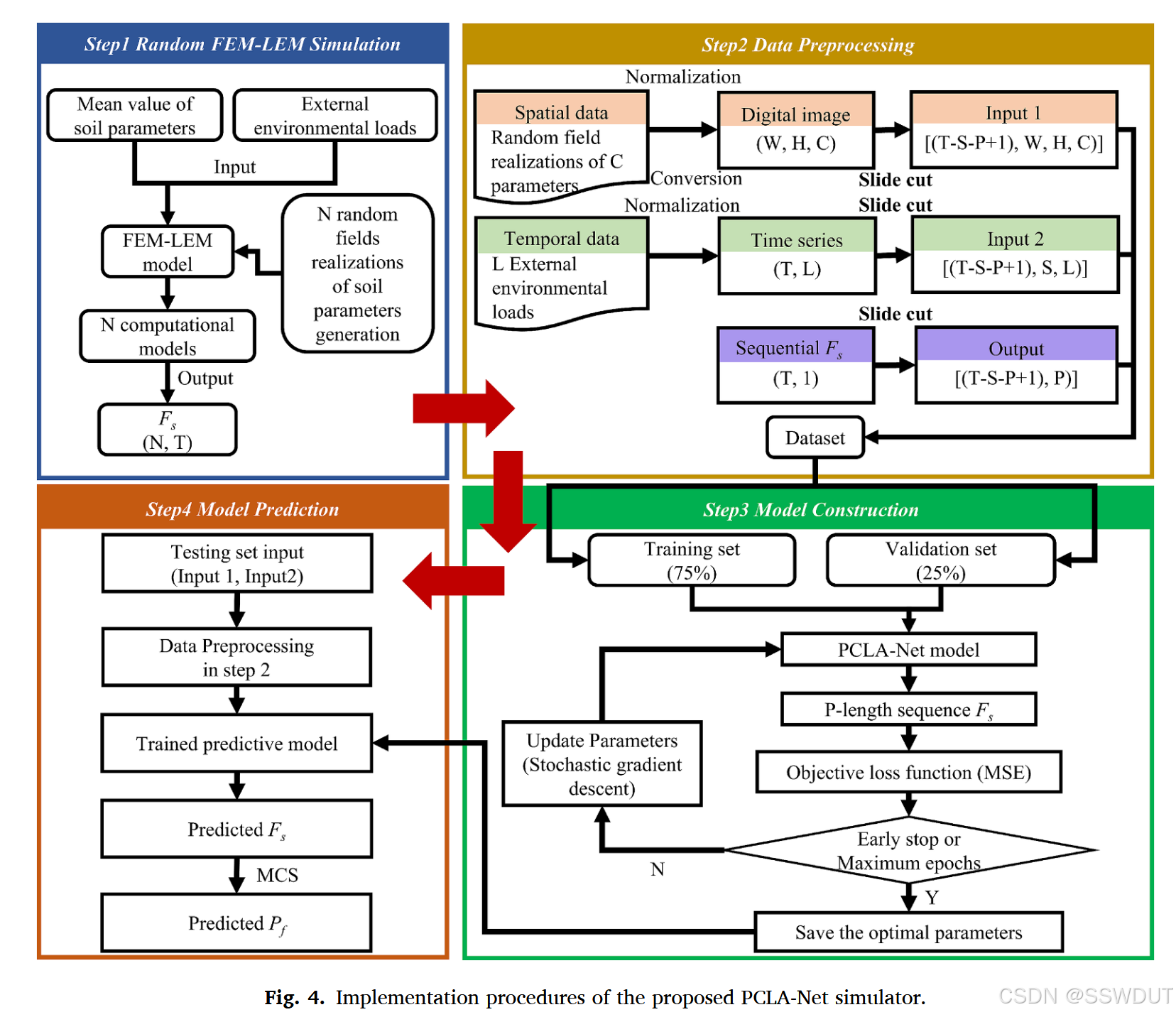
4.1 随机 FEM-LEM 方法(Random FEM-LEM method)
在确定边坡几何形状、外部随时间变化的环境荷载(如降雨、库水位)及土体参数的统计特性(包括概率分布形式、自相关函数、均值、变异系数 CoV 和波动尺度 SoF)之后,进行有限元法(FEM)与极限平衡法(LEM)的序列分析。首先,在考虑土壤渗透率随机场实现的前提下,进行有限元分析以模拟不饱和瞬态渗流过程(受到降雨入渗和库水位波动的影响),从而得到一系列边坡体内部的孔隙水压力(PWP)分布。随后,将该系列 PWP 映射至 LEM 模型中进行边坡稳r定性分析,得到一系列安全系数(Fs)。
本研究采用 Morgenstern 和 Price(M-P)法进行边坡稳定性分析,且土体抗剪强度遵循 Vanapalli 等人(1996)提出的扩展摩尔-库仑破坏准则:
τ f = c ′ + ( σ − u a ) tan ϕ ′ + S e ( u a − u w ) tan ϕ ′ (18) \tau_f = c' + (\sigma - u_a)\tan\phi' + S_e(u_a - u_w)\tan\phi' \tag{18} τf=c′+(σ−ua)tanϕ′+Se(ua−uw)tanϕ′(18)
其中, σ \sigma σ 为总应力, ϕ ′ \phi' ϕ′ 为内摩擦角, c ′ c' c′ 为有效黏聚力, u _ a u\_a u_a 与 u _ w u\_w u_w 分别为孔隙气压与孔隙水压, S _ e S\_e S_e 为有效饱和度。
上述流程重复执行 N N N 次随机场( c ′ c' c′-- ϕ ′ \phi' ϕ′)的实现,从而得到 N N N 组 Fs 序列。该数据集将用于训练 PCLA-Net 模拟器,以完成滑坡灾害的概率性评估。
4.2 数据预处理(Data preprocessing)
前述步骤生成的原始数据需进一步预处理,方可用于训练 PCLA-Net 模拟器。以下对数据预处理技术进行说明,并采用如下符号表示:
一个原始数据样本记为: [ ( x i ( 1 ) , x ( 2 ) ) , y i ] [(x_i^{(1)}, x^{(2)}), y_i] [(xi(1),x(2)),yi]
- x _ i ( 1 ) ∈ R R × C x\_i^{(1)} \in \mathbb{R}^{R \times C} x_i(1)∈RR×C 表示第 i i i 次随机场实现,其中 R R R 为离散网格中高斯积分点数, C C C 为随机场数量(即空间变量土体参数个数);
- x ( 2 ) ∈ R T × L x^{(2)} \in \mathbb{R}^{T \times L} x(2)∈RT×L 表示随时间变化的环境荷载,其中 T T T 为荷载时间长度, L L L 为荷载种类数;
- y _ i ∈ R T y\_i \in \mathbb{R}^{T} y_i∈RT 表示对应于该随机场实现的 Fs 序列。
数据归一化:
为了提升模型性能并缓解梯度爆炸问题,采用 Min--Max 归一化处理 x ( 1 ) x^{(1)} x(1) 与 x ( 2 ) x^{(2)} x(2),将其缩放到区间 [ 0 , 1 ] [0,1] [0,1],如下所示:
v = v − v min v max − v min (19) v = \frac{v - v_{\min}}{v_{\max} - v_{\min}} \tag{19} v=vmax−vminv−vmin(19)
其中, v v v 为归一化后的数据, v _ max v\{\max} v_max 和 v _ min v\{\min} v_min 分别为原始数据中的最大值和最小值。
数字图像转换:
将归一化后的随机场实现 x _ i ( 1 ) x\_i^{(1)} x_i(1) 转换为数字图像格式,以适配 2D CNN 模块的输入需求。该过程将高斯积分点的值映射至图像像素,保持其空间结构和相关性。但自然边坡的几何形状通常不规则,因此采用零填充方式对缺失像素补齐,形成矩形图像(参考 Jiang 等人, 2023;Wang 等人, 2021)。处理后得到的数字图像记为 x ^ _ i ( 1 ) ∈ R W × H × C \hat{x}\_i^{(1)} \in \mathbb{R}^{W \times H \times C} x^_i(1)∈RW×H×C,其中 W W W 和 H H H 分别为图像宽度和高度, C C C 为通道数。
滑动窗口处理:
滑动窗口是一种用于处理时间序列数据的有效技术(Selvin 等人, 2017)。该方法将原始时间序列划分为固定长度的重叠或非重叠子序列(即"窗口"),每个窗口包含一个局部的时间特征,便于模型从中学习。
如图 5 所示,滑动窗口操作包括三个关键参数:
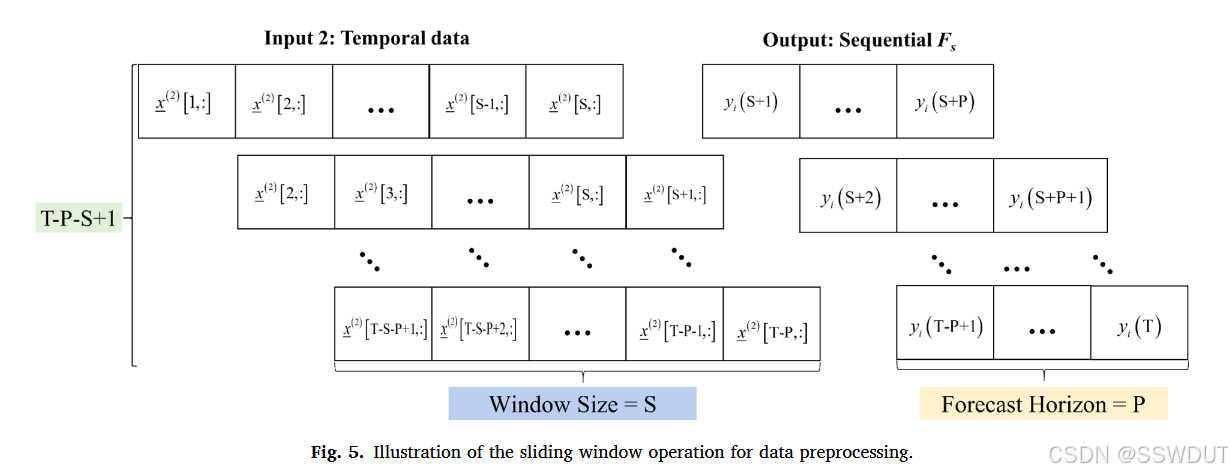
- 窗口长度 S S S(window size);
- 预测步长 P P P(forecast horizon);
- 滑动步幅(设为 1)。
在每次滑动中,利用前 S S S 个时间步的环境荷载数据预测未来 P P P 个时间步的 Fs。对于总时长为 T T T 的时间序列,预处理后可得到:
- 扩展的环境荷载数据 x ~ ( 2 ) ∈ R ( T − P − S + 1 ) × S × L \tilde{x}^{(2)} \in \mathbb{R}^{(T - P - S + 1) \times S \times L} x~(2)∈R(T−P−S+1)×S×L;
- 对应的输出数据 y ~ _ i ∈ R ( T − P − S + 1 ) × P \tilde{y}\_i \in \mathbb{R}^{(T - P - S + 1) \times P} y~_i∈R(T−P−S+1)×P;
- 扩展的空间数据 x ~ _ i ( 1 ) ∈ R ( T − P − S + 1 ) × W × H × C \tilde{x}\_i^{(1)} \in \mathbb{R}^{(T - P - S + 1) \times W \times H \times C} x~_i(1)∈R(T−P−S+1)×W×H×C。
注意:空间数据仅为复制原始随机场实现,以匹配扩展后的时间序列维度,因为其在整个时间段内保持不变。
4.3 其他步骤(Other steps)
完成数据预处理后,开始训练 PCLA-Net 模拟器。数据集被划分为训练集(75%)与验证集(25%)。采用随机梯度下降(SGD)算法在每一轮迭代中更新网络参数,最终返回最优模型参数。
训练结束的条件包括:
- 达到提前停止(early stopping)准则;
- 或达到最大训练轮数。
提前停止机制有助于防止模型过拟合。
训练完成后,可将基于蒙特卡罗模拟生成并经同样预处理的测试集输入至 PCLA-Net 模拟器中,预测给定预测步长 P P P 对应的一系列 Fs 值,并据此计算失效概率 P _ f P\_f P_f。
5. 案例研究(Case study)
5.1 工程背景描述(Project description)
Liangshuijing滑坡(Liangshuijing,简称 LSJ)位于中国重庆市云阳县,处于长江右岸,距离三峡大坝上游约 300 公里。该滑坡估算体积为 2.63 × 1 0 6 m 3 2.63 \times 10^6\ \text{m}^3 2.63×106 m3,整体呈明显的 U 形平面形态。如图 6(a) 所示,为该滑坡的典型地质剖面。滑坡相邻的河床最低高程约为 50 m,滑坡体高程范围为 100--320 m,平均宽度约为 370 m。
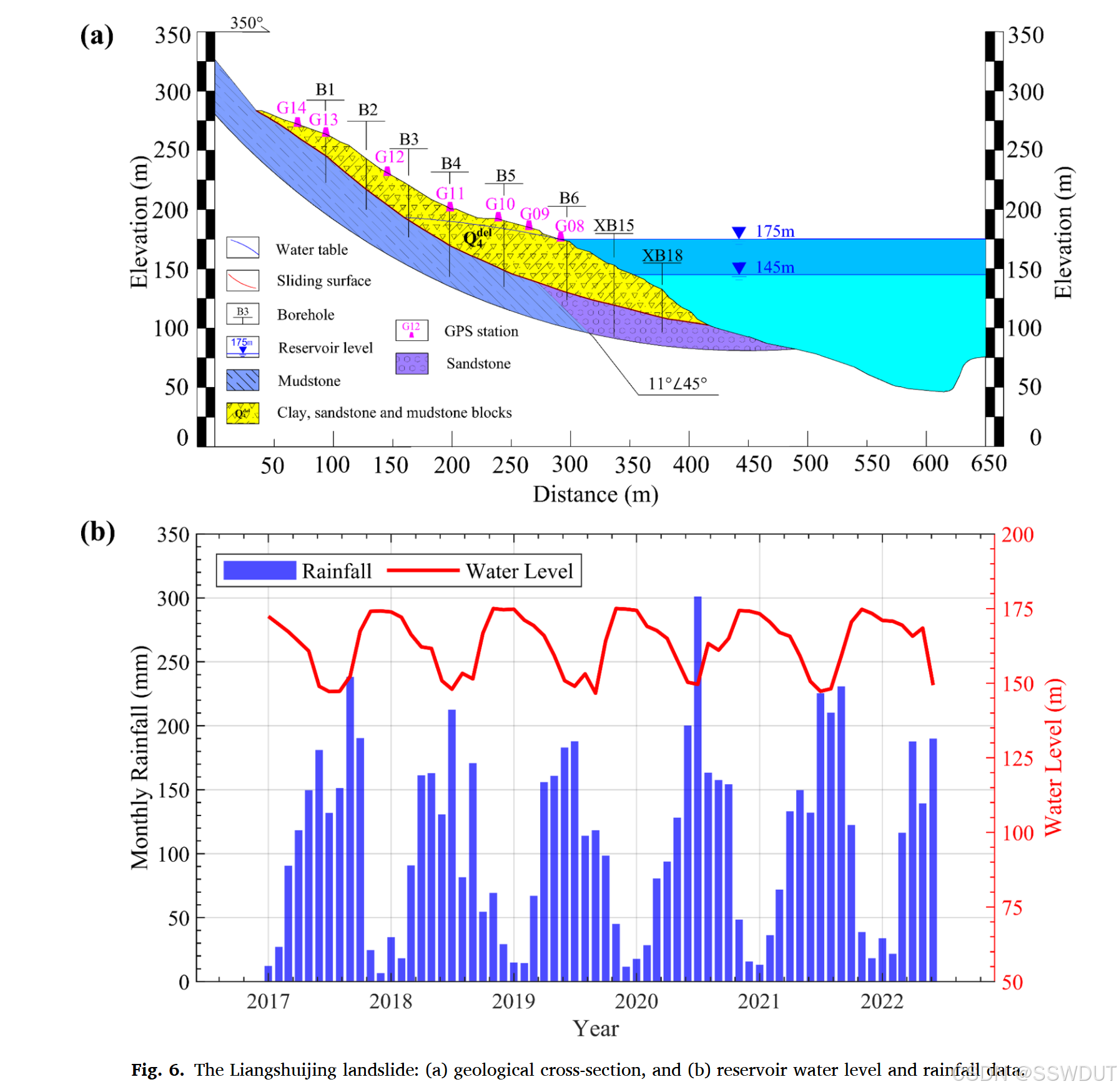
滑坡堆积物主要由第四纪粉质粘土与角砾、岩屑夹层组成,岩屑成分包括砂岩与泥岩。滑坡基岩为侏罗系沙溪庙组,具有砂岩与泥岩互层的沉积结构。由于滑坡位于水库库区,其稳定性受季节性降雨与库水位波动的显著影响。图 6(b) 展示了 LSJ 滑坡从 2017 年 1 月至 2022 年 6 月的历史降雨与库水位记录。
5.2 数值模拟(Numerical simulation)
本研究采用 GeoStudio 软件开展顺序 FEM-LEM 联合建模。在非稳态渗流分析中,边坡模型施加混合边界条件。对于处于淹没状态的边坡部分,设置总水头边界条件,其水头随库水位在 145--175 m 范围内变化;对于高于水位的坡面部分,则施加与实测降雨强度相等的通量边界条件。
在滑坡堆积体中允许非饱和土与饱和土之间的状态转换;而基岩部分则被视为饱和区,并在其左侧和底部边界施加零通量边界条件,模拟为不透水屏障。这些简化假设可能略微高估孔隙水压力(PWP),从而提供更保守的稳定性评估。虽然这种保守性可能影响数值模拟的绝对精度,但对于地质灾害评估而言提供了安全裕度,且不会显著影响所提出 PCLA-Net 模型的对比评估效果。
表 1 总结了 LSJ 滑坡随机 FEM-LEM 分析中使用的关键土工参数。其中:
表1 梁水井滑坡的主要土壤参数
| 土壤参数 | 滑坡堆积层 | 基岩 |
|---|---|---|
| 有效黏聚力 c ′ c' c′ (kPa) | 21.48 | 5650 |
| 变异系数 CoV | 0.25 | --- |
| 有效摩擦角 ϕ ′ \phi' ϕ′ (°) | 25.03 | 47.04 |
| 变异系数 CoV | 0.20 | --- |
| 饱和渗透系数 k _ s k\_s k_s (m/s) | 3.7 × 1 0 − 6 3.7 \times 10^{-6} 3.7×10−6 | 1.3 × 1 0 − 9 1.3 \times 10^{-9} 1.3×10−9 |
| 变异系数 CoV | 0.5 | --- |
| 饱和单位重 γ _ s \gamma\_s γ_s (kN/m³) | 23.8 | 25.3 |
| 饱和体积含水量 θ _ s \theta\_s θ_s | 0.340 | --- |
| 残余体积含水量 θ _ r \theta\_r θ_r | 0.030 | --- |
注释 : γ _ s \gamma\_s γ_s 表示饱和单位重; θ _ s \theta\_s θ_s 和 θ _ r \theta\_r θ_r 分别为饱和体积含水量和残余体积含水量。
- 饱和渗透系数 k _ s k\_s k_s、有效黏聚力 c ′ c' c′、有效摩擦角 ϕ ′ \phi' ϕ′ 被建模为对数正态随机场;
- 其他参数视为常数;
- Van Genuchten--Mualem 模型(VGM)的参数 a a a 和 n n n 分别取为 24 kPa 和 1.79;
- c ′ c' c′ 与 ϕ ′ \phi' ϕ′ 的相关系数设为 0.49, k _ s k\_s k_s 与其余两者相互独立。
这些参数基于分层贝叶斯模型(Ching 等人, 2021)推导而得,该模型整合了有限的实测数据与大型间接数据库信息。
三类随机场的垂直与水平波动尺度(Scale of Fluctuation, SoF)分别设为 3.5 m 和 30 m。随机场离散为 2310 个单元格,每个单元格在水平和垂直方向的边长分别为 6 m 与 0.8 m。
5.3 PCLA-Net 模拟器的实现(PCLA-Net implementation)
本研究中使用顺序 FEM-LEM 模型进行了 1500 次蒙特卡罗模拟(MCS)以获得基准结果。该次数在计算资源与失效概率 P _ f P\_f P_f 的统计可靠性(以变异系数 CoV 衡量)之间取得良好平衡。
降雨与库水位数据来源为 2017 年 1 月至 2022 年 6 月。PCLA-Net 的训练采用 2017 年 1 月至 2021 年 6 月(共 54 个时间步)期间的数据,并将其划分为训练集(75%)与验证集(25%)。剩余时间段(2021 年 7 月至 2022 年 6 月,共 12 个时间步)作为测试集。
在 54 个时间步的数据中,最大 P _ f P\_f P_f 的 CoV 值出现在第 23 个时间步,为 0.1485。此值在工程界认为是可接受的,表明 1500 次 MCS 在统计精度与计算效率之间取得了良好平衡。
图 7 展示了如何将一次 k _ s k\_s k_s 随机场实现转换为数字图像通道。图像包含 2310 个像素点,对应于离散网格单元的高斯积分点。黑色像素表示零填充区域。在该处理过程中,为了降低图像维度,剔除了基岩区域,仅保留滑坡堆积体。图像已旋转,使滑坡的坡脚与坡顶处于同一水平线上。 c ′ c' c′ 与 ϕ ′ \phi' ϕ′ 的随机场亦同样处理。
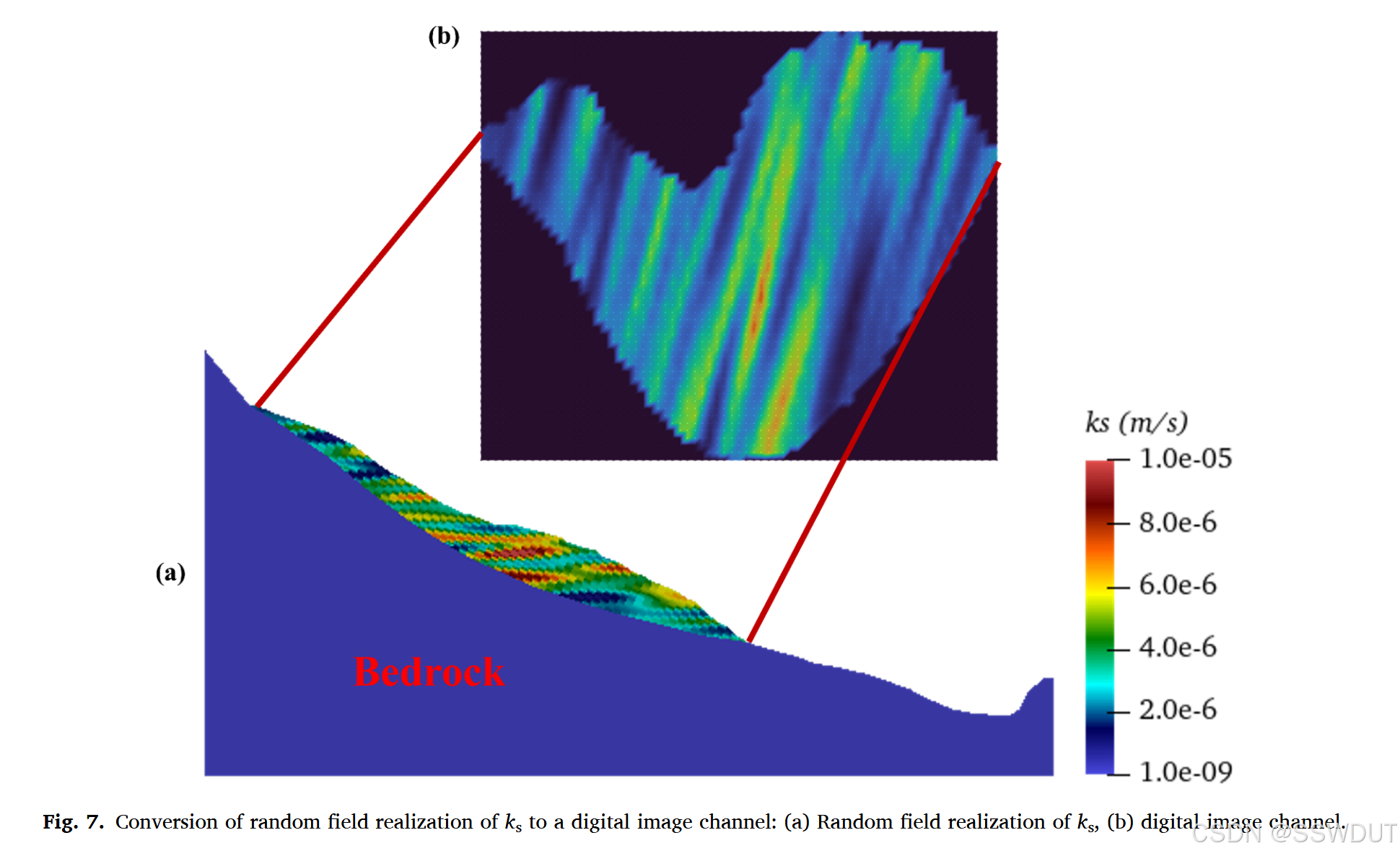
最终输入图像维度为 71 × 59 × 3 71 \times 59 \times 3 71×59×3(宽 × 高 × 通道),其中 3 表示三种空间变量土工参数。
图 8 展示了 PCLA-Net 模拟器的结构示意图与数据流示例,具体包括:
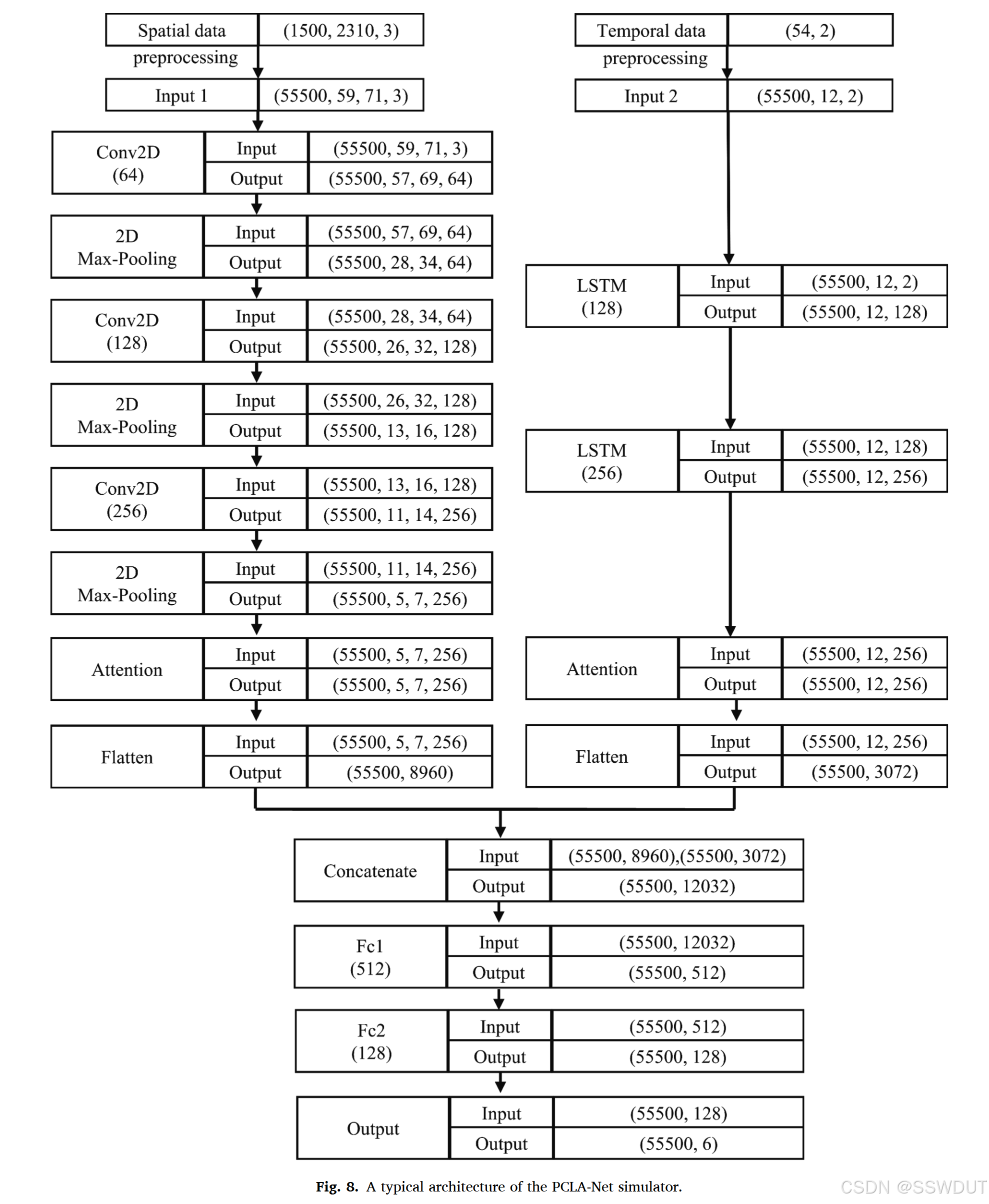
- 三个随机场共 1500 次实现;
- 时间序列数据包含 54 个时间步的降雨与水位(2017 年 1 月至 2021 年 6 月);
- 滑动窗口参数设为窗口长度 S = 12 S = 12 S=12,预测步长 P = 6 P = 6 P=6。
根据图 5 所示的滑动窗口方法,时间序列( T = 54 T = 54 T=54)被划分为多个长度为 S = 12 S = 12 S=12 的输入子序列与长度为 P = 6 P = 6 P=6 的预测序列。采用步长为 1 的滑动操作后,可得到:
T − P − S + 1 = 37 个子序列 T - P - S + 1 = 37\ \text{个子序列} T−P−S+1=37 个子序列
因此,训练数据量为:
1500 × 37 = 55500 组输入-输出样本 1500 \times 37 = 55500\ \text{组输入-输出样本} 1500×37=55500 组输入-输出样本
该处理显著扩充了训练数据集,增强了模型的泛化能力。
此外,在 2D CNN 模块中,卷积层使用核大小为 ( 3 , 3 ) (3, 3) (3,3),步幅为 1;池化层使用最大池化操作,尺寸为 ( 2 , 2 ) (2, 2) (2,2)。该模块包含三组卷积-池化-激活结构,卷积核数量分别为 64、128 和 256,激活函数为 ReLU。
LSTM 模块包含两层,分别具有 128 与 256 个单元。使用 TensorFlow-GPU 框架构建并训练 PCLA-Net 模拟器。
表 2 总结了本研究中采用的超参数设置。
表2 超参数设置及计算机配置
| 参数 | 设置 |
|---|---|
| 优化器 | Adam |
| 学习率 | 0.00001 |
| 动量Momentum | 0 |
| 批量大小 | 100 |
| 最大训练轮数 | 1000 |
| 提前停止轮数 | 30 |
备注:
- CPU:Intel Core i9-10980XE
- GPU:NVIDIA GeForce RTX 4080 16 GB
- 内存:256 GB RAM
- 环境:Python 3.9.0 & TensorFlow-GPU 2.7.0
为解决神经网络的随机性问题,实施了以下关键措施:
- 模型运行 50 次,以提高性能评估的可靠性与一致性;
- 所有运行初始化参数一致,减少因随机初始化带来的波动;
- 所有实验采用相同的超参数设置,确保模型训练与结果可比性。
5.4 PCLA-Net 模拟器的验证
滑动窗口操作是处理时间序列数据的常用方法。选择合适的窗口大小至关重要,它会显著影响数据特征的提取,从而影响深度学习模型的预测精度。在本研究中,PCLA-Net 模拟器通过不同窗口大小的设置进行了验证。
首先,图 9(a) 展示了 PCLA-Net 的训练过程。训练集和验证集的 Fs 均方根误差(RMSE)在初期迅速下降,并收敛至相对稳定的数值。训练在第 358 轮左右由于满足提前停止条件而结束。该收敛趋势表明模型学习有效,并具备良好的泛化能力,能够对 Fs 做出准确预测。
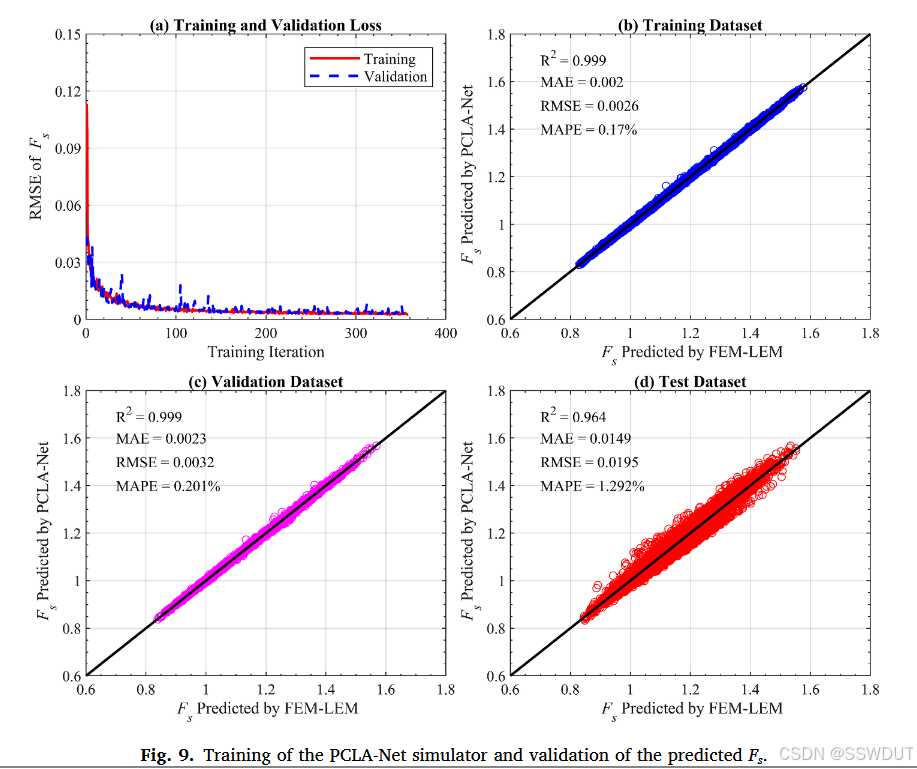
图 9(b)、©、(d) 分别展示了基于窗口大小为 12、预测步长为 1 时,PCLA-Net 模拟器对训练集、验证集和测试集 Fs 值的预测与 FEM-LEM 模型计算值的对比。训练与验证集基于 2017 年 1 月至 2021 年 6 月的 54 个时间步数据与 1500 次随机场实现,测试集则为 2021 年 7 月至 2022 年 6 月的 12 个时间步数据和同样数量的随机场。
散点图在所有数据集上均表现出强线性相关性。特别是在图 9(d) 中,测试集的确定系数( R 2 R^2 R2)达到 0.9639 ,平均绝对误差(MAE)为 0.0149 ,RMSE 为 0.0195 ,平均绝对百分比误差(MAPE)为 1.292%,充分说明 PCLA-Net 能够成功捕捉输入特征(例如空间与时间数据)与 Fs 输出之间的内在关系,对未见数据具备出色的预测能力。
在不同窗口大小的实验中,所有超参数均保持一致(见表 2)。网络结构中,尤其是 LSTM 层,会根据不同输入尺寸自适应调整,但整体架构不变。
图 10(a) 和 (b) 展示了基于测试集的 PCLA-Net 在不同窗口大小(1 至 15)与固定预测步长为 1 时的性能表现。图 10(a) 描述了窗口大小与预测 Fs 的 MAE 与 R 2 R^2 R2 的关系。随着窗口大小增大,MAE 整体呈下降趋势, R 2 R^2 R2 则整体上升。二者在较小窗口尺寸下变化剧烈,在尺寸增大后趋于平稳。特别地,窗口大小为 12 时 MAE 达到最小, R 2 R^2 R2 达到最大,表明该窗口大小在误差控制与模型拟合间达到了最优平衡。
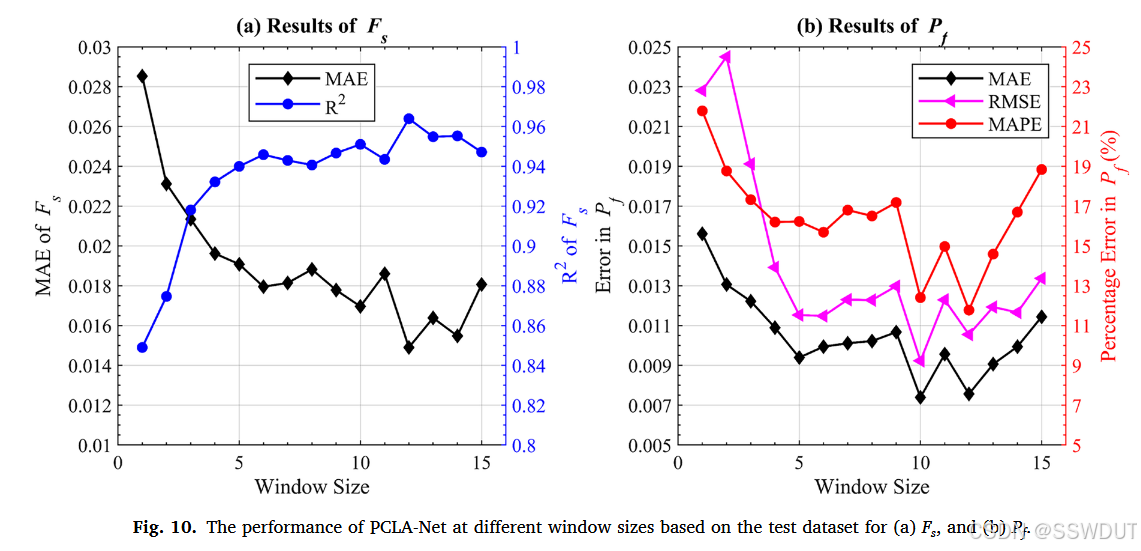
此外,图 10(b) 展示了窗口大小对 Pf 预测的 RMSE、MAE 与 MAPE 的影响。三个指标在窗口增大初期显著下降,随后趋于稳定,并在更大尺寸时出现轻微波动。它们的最小值均出现在窗口大小为 12 时,进一步验证了该尺寸在 Pf 预测中同样具备最高准确度和最低误差。
图 11 进一步比较了使用窗口大小 12、预测步长为 1 的 PCLA-Net 模拟器与 FEM-LEM 方法所计算的 Pf。模拟器使用了 2018 年 1 月至 2022 年 6 月的数据进行训练。无论是训练集、验证集还是测试集,PCLA-Net 对 Pf 的预测结果都与 FEM-LEM 的结果高度吻合,显示出极佳的准确性与泛化能力。
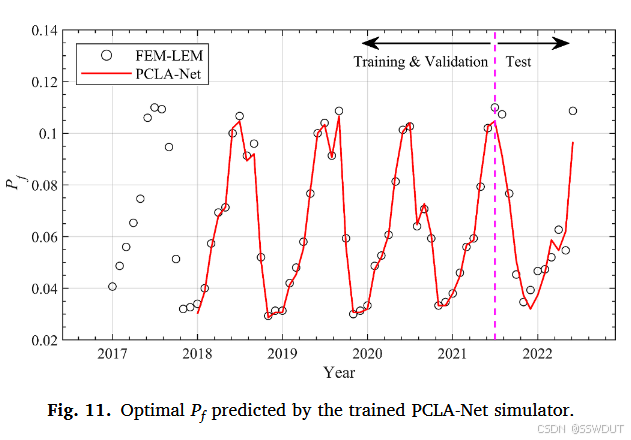
此外,Pf 呈现出年周期性变化特征,PCLA-Net 模拟器能够准确捕捉该变化趋势。即使在测试集上,模型仍能可靠地追踪 Pf 的动态波动,与 FEM-LEM 模型计算结果高度一致,显示出其在时间依赖型失稳概率预测中的强大能力。
5.5 注意力机制的影响
基于窗口大小为 12、预测步长为 1 以及测试数据集,对比了是否引入注意力机制的 PCLA-Net 模型性能。实验表明,注意力机制的引入在 Fs 和 Pf 的预测性能上均带来显著提升。
如表 3 所示,在 Fs 预测中,加入注意力机制后 R 2 R^2 R2 提升至 0.9639 ,而不使用注意力机制的模型为 0.9556 。此外,MAE、RMSE 和 MAPE 也均显著下降,显示出更高的预测精度。
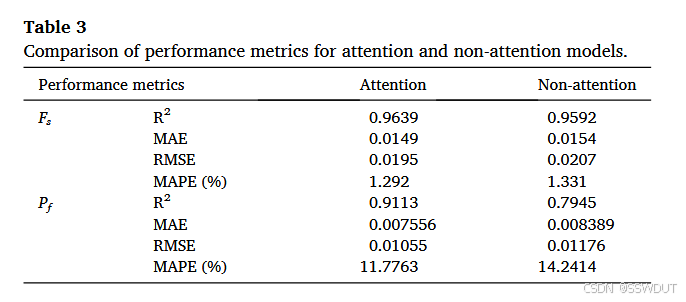
在 Pf 的预测中,注意力机制带来的效果更加明显。引入注意力机制后, R 2 R^2 R2 提高至 0.9113 ,MAE 降至 0.007556 ,RMSE 为 0.01055 ,MAPE 为 11.7763% ,均优于未使用注意力机制的模型( R 2 R^2 R2 为 0.7945,MAE 为 0.008389,RMSE 为 0.01176,MAPE 为 14.2414%)。
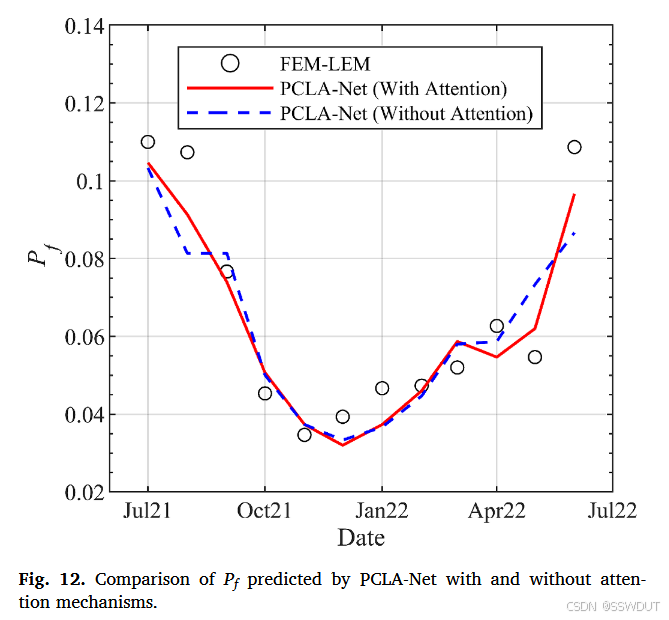
图 12 对比了两种模型对 Pf 曲线的预测结果。引入注意力机制的模型对 FEM-LEM 基准结果的拟合更加紧密,尤其在 Pf 的时间波动和峰值捕捉上表现更优,进一步证明了其在模拟边坡系统动态行为方面的准确性与敏感性。
5.6. 预测时间跨度(Forecast Horizon, FH)的影响
为进一步评估 PCLA-Net 模拟器的预测精度,本文研究了不同预测时间跨度(forecast horizons, FH)下的表现。需要说明的是,PCLA-Net 的训练基于 1500 个随机场实现样本及包含 54 个时间步(即 2017 年 1 月至 2021 年 6 月)的降雨与水位波动时序数据。分析中采用窗口大小 S = 12 S = 12 S=12,该值为图 10 中得出的最优值。
本文实验了四种预测时间跨度( FH = 1 , 3 , 6 , 12 \text{FH} = 1, 3, 6, 12 FH=1,3,6,12),表 4 展示了测试集下各 FH 对应的 F s F_s Fs 与 P f P_f Pf 预测性能指标。结果表明,随着预测跨度的增加,模型预测精度呈逐步下降趋势。但这一变化较为温和,例如 F s F_s Fs 的 R 2 R^2 R2 从 0.9639 降至 0.9330。对于 P f P_f Pf 预测而言, R 2 R^2 R2 从 0.9113 降至 0.5525,MAE 从 0.007556 升至 0.01389,RMSE 从 0.01055 升至 0.01807,MAPE 从 11.7763% 升至 21.3423%。尽管误差有所上升,但整体仍在可接受范围内,表明 PCLA-Net 模拟器在短期与长期边坡稳定性预测方面均具有稳健的性能与可靠性。
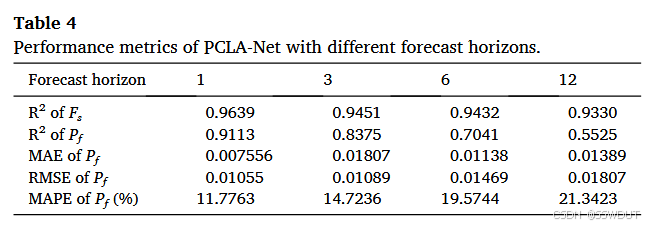
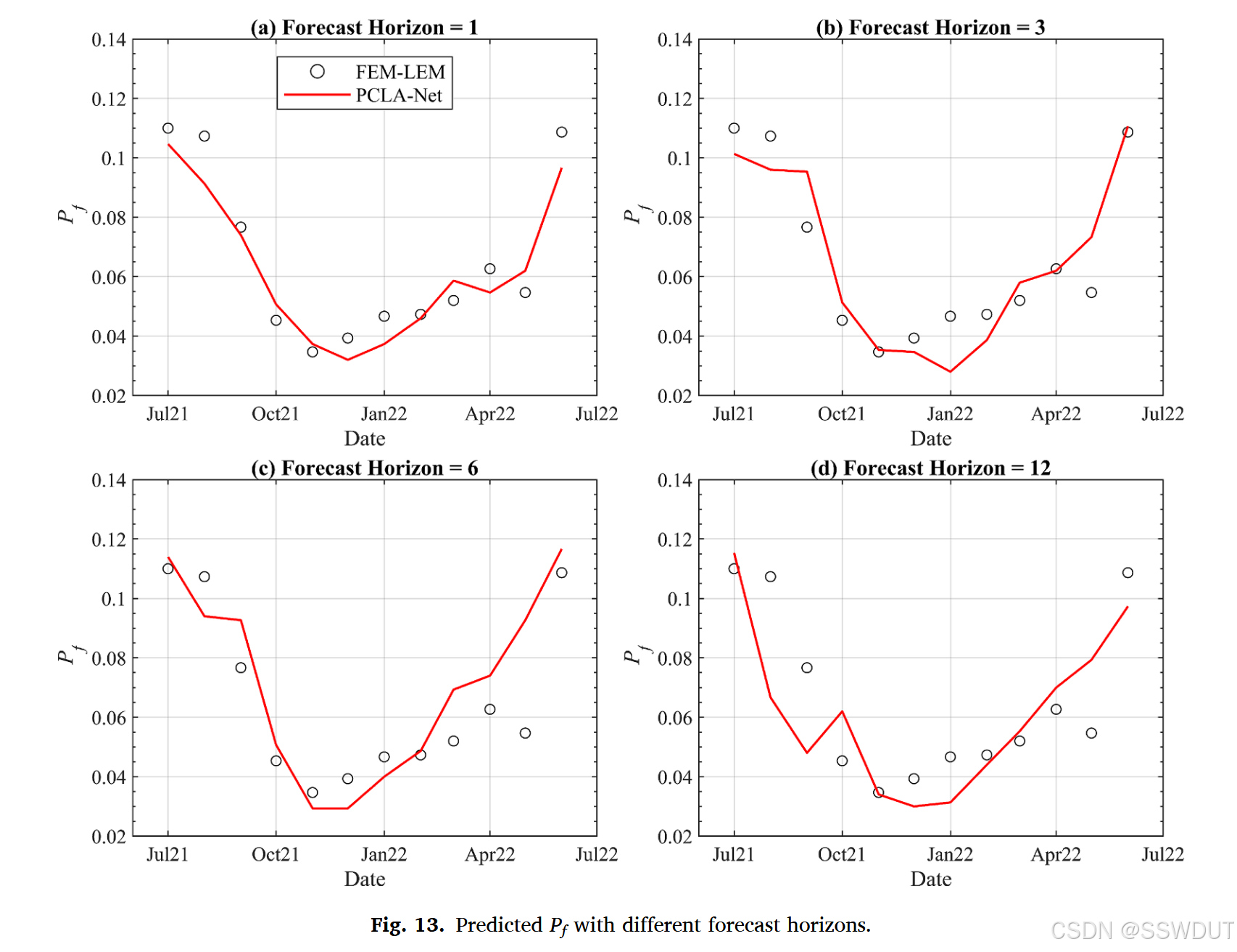
图 13 更进一步比较了四种预测跨度(FH = 1、3、6、12)下的 P f P_f Pf 预测曲线与基准 FEM-LEM 结果。PCLA-Net 能够准确捕捉 P f P_f Pf 的整体时间变化趋势。对于较短的预测跨度(FH = 1 与 FH = 3),其预测曲线在幅值与时序波动方面均与 FEM-LEM 曲线高度一致。对于较长跨度(FH = 6 与 FH = 12),虽然部分时段出现轻微偏差,但整体趋势仍被有效捕捉。特别是在 FH = 12 的最具挑战性场景下,模型依然能准确复现 P f P_f Pf 的季节性变化及系统整体行为。
这表明 PCLA-Net 模拟器具备学习与泛化复杂时空关系的能力,且在延长时间尺度下保持高预测精度,适合应用于滑坡灾害的长期预报。这种跨时间尺度的表现力使其在滑坡风险评估中既适用于实时预警,也可用于战略规划与防灾决策。
6. 与其他技术的对比
本节对 PCLA-Net 模拟器与 LSTM、1D CNN 两种方法在同一预测任务下进行全面比较。为确保公平性,所有方法均采用预测跨度 FH = 1 \text{FH} = 1 FH=1,因为此时三种方法的预测精度最佳。
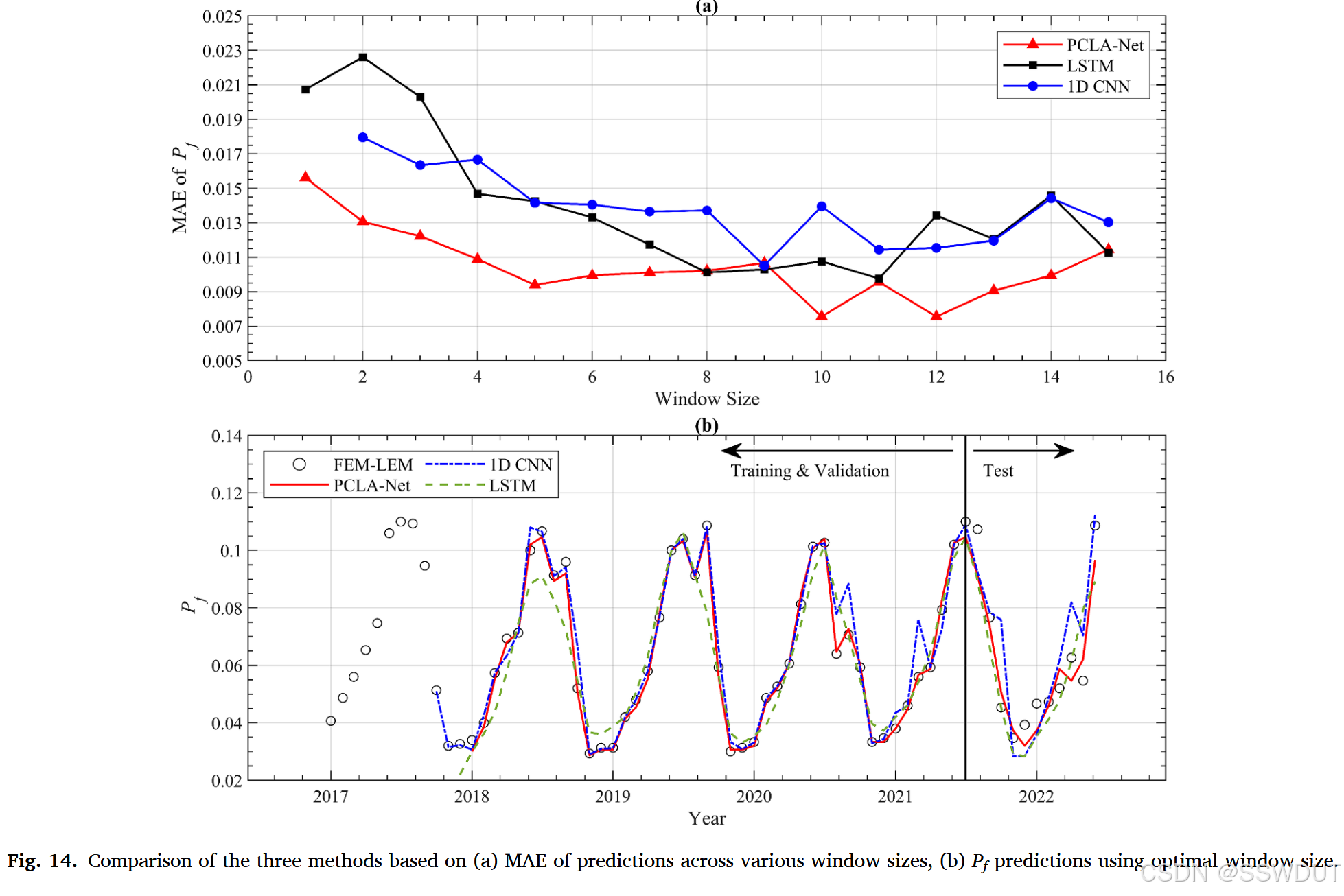
这两种方法的实现过程参考 Wang 等(2023)文献。图 14(a) 首先对比了不同滑动窗口大小下测试集上 P f P_f Pf 的 MAE 值(PCLA-Net 的结果来自图 10)。三种方法均使用 1500 个随机场样本与 54 个时间步(2017 年 1 月至 2021 年 6 月)训练,测试集则为相同随机场样本配合 12 个时间步(2021 年 7 月至 2022 年 6 月)。
结果显示,PCLA-Net 在几乎所有窗口大小下均表现优于 LSTM 与 1D CNN,拥有更低的 MAE 值。LSTM 与 1D CNN 的最优窗口大小分别为 11 和 9。值得注意的是,PCLA-Net 在窗口大小仅为 4 的情况下已能达到 LSTM 与 1D CNN 在最优窗口下的预测精度,表明 PCLA-Net 在学习时间序列特征方面更高效,仅需较短的子序列即可完成建模。
表 5 总结了三种方法在其最优窗口大小下的 P f P_f Pf 预测性能指标。PCLA-Net 明显为最佳模型,其 R 2 R^2 R2 达到 0.9113,MAE、RMSE 和 MAPE 分别为 0.007556、0.01055 和 11.7763%。LSTM 表现次之,1D CNN 最差。
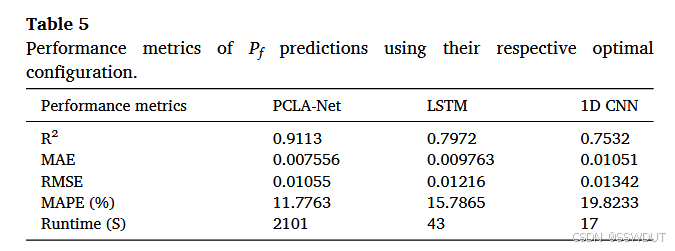
需要强调的是,LSTM 与 1D CNN 模型直接在 P f P_f Pf 空间中工作(Wang et al., 2023),无法预测 F s F_s Fs。这构成了其一大局限性,即未能直接利用随机场信息进行端到端学习。而 PCLA-Net 可实现随机场到 F s F_s Fs 的端到端预测,具有更高的数据解释力与泛化能力。
图 14(b) 显示了三种方法基于各自最优窗口大小的 P f P_f Pf 时间演化曲线。图中圆点为 FEM-LEM 的基准值。PCLA-Net 预测结果与基准值高度吻合,准确反映了训练、验证及测试集中的复杂波动特征。
三种方法的计算成本也进行了比较:PCLA-Net 模拟器的运行时间为 2101 秒,而 LSTM 与 1D CNN 分别仅需 43 秒与 17 秒。然而,计算成本更合理的衡量方式是其所需训练样本数量。
图 15 展示了三种模型在不同训练样本数下的性能对比。所有方法均基于最优窗口参数。图 15(a) 为测试集上 P f P_f Pf 的 MAE,图 15(b) 展示了 PCLA-Net 的 F s F_s Fs 预测 R 2 R^2 R2 和 MAPE。
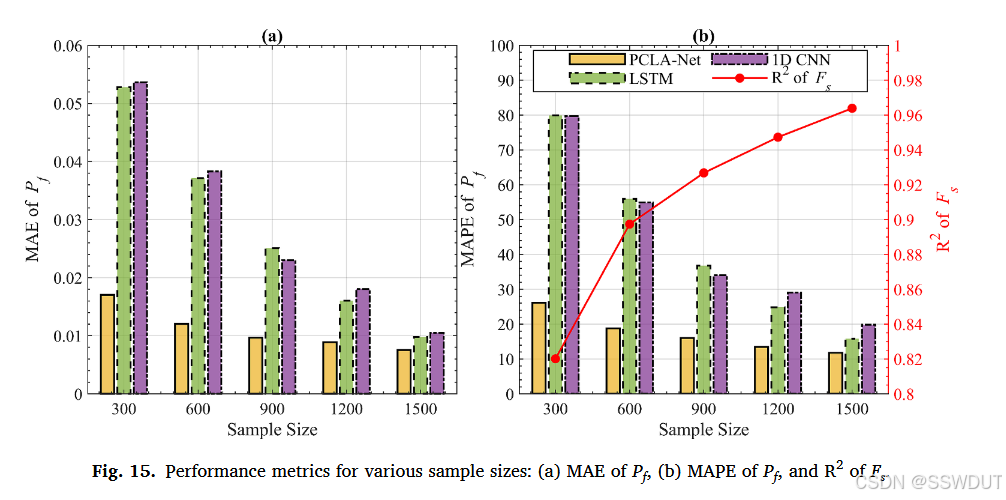
在所有样本量下,PCLA-Net 始终保持最低误差,优势在小样本场景下尤为明显。例如,PCLA-Net 在仅使用 300 个样本时已可达成 MAE = 0.01703,MAPE = 26.106%;而 LSTM 与 1D CNN 需超过 1000 个样本方能达到相似性能。若样本数较小(如 300),LSTM 与 1D CNN 无法实现合理预测(MAE 分别为 0.05278 与 0.05364,MAPE 分别为 79.9068% 与 79.7226%)。
这种差异源于 LSTM 与 1D CNN 本质上非端到端方法,需先估计 P f P_f Pf 才能进行训练。因此,必须有至少 1200--1500 个样本以确保 P f P_f Pf 的估计精度。
这充分证明了 PCLA-Net 在数据稀缺条件下对时间变异可靠性动态的建模能力,同时也显示出其随数据增多而进一步提升的潜力。根据图 15 结果,PCLA-Net 达到收敛精度所需训练样本约为 600。
图 16 展示了在 300 与 900 样本下三种模型预测的 P f P_f Pf 曲线对比。在 300 样本条件下,PCLA-Net 展现出卓越的预测性能,准确捕捉季节性波动(峰值与谷值),并与基准值高度一致。而 LSTM 与 1D CNN 均未能捕捉季节性特征,且系统性低估 P f P_f Pf。
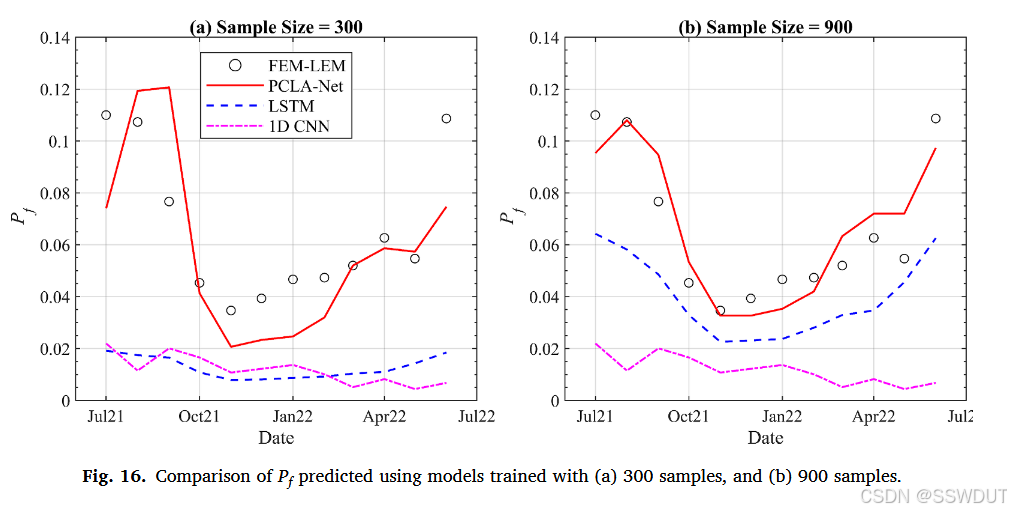
样本数增加至 900 后,三种模型预测能力均有所提升,其中 PCLA-Net 依然表现最优。例如,2021 年 11 月的预测值为 0.0327,真实值为 0.0347;2022 年 12 月预测值为 0.0327,真实值为 0.0393,进一步验证其对时空数据动态建模的准确性。相比之下,虽然 LSTM 能识别出季节性模式,但在整个测试集时间范围内依然低估 P f P_f Pf;1D CNN 仍未能识别出季节性变化。
7. 结论
综上所述,本研究提出了一种新颖的端到端混合深度学习模型------PCLA-Net,用于滑坡灾害的时变概率评估。通过集成二维卷积神经网络(2D CNN)模块与长短期记忆网络(LSTM)模块并辅以注意力机制,PCLA-Net 能够有效捕捉土壤性质的空间变异性与时间变化的环境载荷的综合影响,实现输入参数到安全系数预测的直接映射。
PCLA-Net 的架构有效处理了非耦合空间与时间数据的复杂性,并通过注意力机制对提取的特征进行精炼,从而获得高精度的预测结果。以Liangshuijing滑坡实例为案例,验证了 PCLA-Net 的预测准确性与稳健性。同时,研究了注意力机制和滑动窗口大小对模型性能的影响。
综合比较研究显示,PCLA-Net 在准确性与效率的双重考量下,在几乎所有滑动窗口尺寸范围内均优于现有的 LSTM 和一维卷积神经网络(1D CNN)方法。与其他技术相比,PCLA-Net 模拟器所需的训练数据量显著减少,数据需求至少降低了 50%,却能达到相当的预测性能。
PCLA-Net 的这些优势归功于其端到端架构,使其能够直接且更全面地从空间和时间特征中学习,从而优于仅依赖时间序列学习的 LSTM 和 1D CNN。
PCLA-Net 在地质工程数字孪生及基于在线学习的早期预警系统中展现出极大潜力。其高效处理空间与时间数据的能力,特别适合于实时或近实时的地质系统连续监测与动态更新。这种性能提升有望带来更准确、及时的滑坡灾害预测,显著改善易灾区域的风险评估与管理策略。
然而,需指出的是,当前版本的 PCLA-Net 仅限于处理非耦合的空间和时间数据。未来研究应聚焦于改进模型架构,使其能够有效适应耦合及非耦合的时空数据,为滑坡灾害评估提供更全面的解决方案。