Diffuse and Disperse: Image Generation with Representation Regularization

Regularization

这篇论文的核心思想非常简洁、巧妙：通过在扩散模型中增加一个简单的"分散损失"（Dispersive Loss），来规范模型的内部特征表示，从而在不增加模型参数、不依赖外部数据的情况下，显著提升图像生成质量。

下面，我们将围绕论文中的图表和公式，一步步拆解它的工作原理和贡献。

论文核心思想概览

问题 : 传统的扩散模型（Diffusion Models）专注于一个目标：去噪/重建。它们的损失函数是回归性质的，但很少关注模型内部学习到的"特征表示"（Representation）的质量。这与表示学习（Representation Learning）领域的发展是脱节的。
现有方案的不足: 最近的REPA方法尝试引入表示学习，但它依赖一个巨大的、预训练好的外部模型来"指导"生成模型的内部表示。这种方法成本高、依赖外部数据，很难说清效果是来自表示学习本身，还是来自外部模型的强大能力。
本文方案 (Dispersive Loss) : 作者提出了一种"自给自足"的方案。在标准的去噪损失之外，增加一个正则化项，这个正则化项只做一件事：让同一批次（batch）中不同图像的内部特征在特征空间里相互"推开"，尽可能地分散。
核心洞察 : 这个"推开"的操作，类似于对比学习（Contrastive Learning）中的"推开负样本"。但它巧妙地省略了"拉近正样本"这一步。为什么可以省略？因为扩散模型本身的去噪任务，天然地起到了"对齐"（Alignment）作用，迫使模型为每个带噪输入生成正确的目标输出。因此，整个方法就像一个"没有正样本对的对比学习"，非常简洁。

核心概念：分散损失 (Dispersive Loss)

让我们从论文的门面------图1 和公式1开始。

Figure 1: Dispersive Loss for Generative Modeling

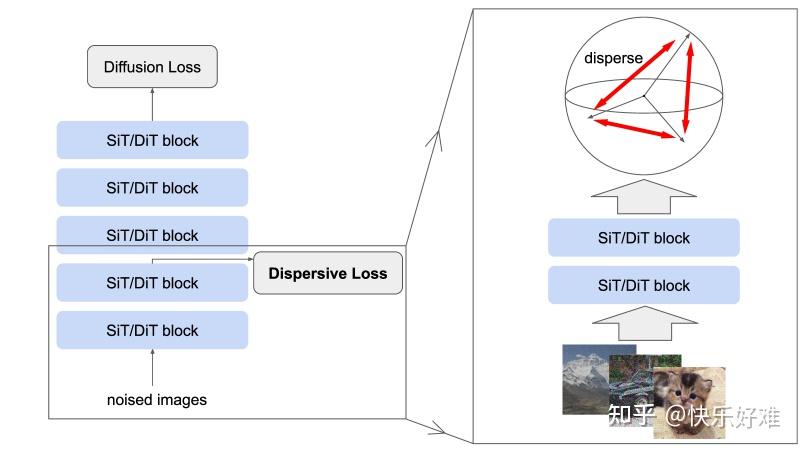
这张图直观地展示了论文的核心架构。

左图 : 这是一个标准的扩散模型（如DiT或SiT），它接受带噪图像作为输入，然后预测噪声或原始图像。论文的改进在于，从模型的中间某一层 （intermediate block）提取出特征表示，然后在这个特征上施加一个分散损失 (Dispersive Loss)。这个新损失与模型原有的扩散损失（Diffusion Loss）相加，共同指导模型训练。
右图: 进一步放大了细节。对于一个批次（batch）里的多个带噪图像，它们经过网络的前几层后会得到各自的中间特征。分散损失的作用就是让这些特征在隐空间中相互排斥、分散开来。

关键优势 (从图中可以看出):

即插即用 (Plug-and-play): 无需改变模型结构，只需在中间层加一个损失函数。
开销极小: 它利用了前向传播过程中已经计算出的中间特征，几乎不增加计算负担。
自给自足: 不依赖任何外部模型或数据。

公式 (1): 核心目标函数

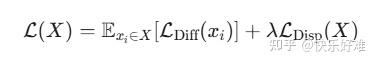
这个公式是整个方法的数学表达：

$\\mathcal{L}(X)$ : 整个批次
XX
的总损失。
$\\mathcal{L}_{\\text{Diff}}(x_i)$ : 单个样本
xixi
的标准扩散损失（例如，预测噪声和真实噪声之间的均方误差）。这是模型的主任务。
$\\mathcal{L}_{\\text{Disp}}(X)$ : 作用于整个批次
XX
的分散损失。这是一个正则化项。
$\\lambda$ : 一个超参数，用来平衡主任务和正则化项的重要性。

分散损失的具体形式

作者是如何设计 $\\mathcal{L}_{\\text{Disp}}$ 的呢？他们从经典的对比学习损失InfoNCE出发，推导出了一个"无正样本"的版本。

公式 (2) & (3): 从对比学习 (InfoNCE) 出发

标准的InfoNCE损失可以写成（公式3的形式更直观）：

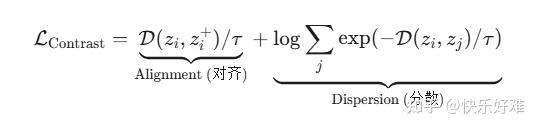
$(z_i, z_i\^+)$ 是一对正样本（比如同一张图片的不同增强版本）。第一项Alignment的目标是让它们的距离 $\\mathcal{D}$ 尽可能小（拉近）。
$z_j$ 是批次中的所有样本（包括正负样本）。第二项Dispersion的目标是让 $z_i$ 和其他所有样本 $z_j$ 的距离尽可能大（推开）。

公式 (6): 分散损失的最终形式

作者的洞察是：扩散模型的去噪任务已经隐式地处理了"对齐"问题。因此，我们可以大胆地只保留第二项，得到分散损失：

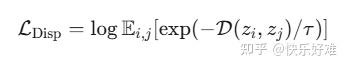
这个公式的含义是：

从一个批次中任意抽取两个样本
ii
和 jj。
计算它们的特征 $z_i$ 和 $z_j$ 之间的距离 $\\mathcal{D}(z_i, z_j)$ 。
目标是让这个距离的指数加权平均值尽可能小，这等价于让所有样本对之间的距离 $\\mathcal{D}$ 尽可能大。
$\\tau$ (温度系数) 控制着"推开"的强度。

Table 1: 分散损失的变体

这张表格清晰地展示了"分散损失"是如何从各种"对比损失"中简化而来的。

InfoNCE: 如上所述，只保留了log-sum-exp项。
Hinge: 经典的对比损失包含正样本项和负样本项。分散损失只保留了负样本项，即当两个样本距离小于某个阈值 $\\epsilon$ 时，才施加一个"推开"的力。
Covariance : Barlow Twins等方法的目标是让特征的协方差矩阵接近单位矩阵（对角线为1，非对角线为0）。对角线为1是"对齐"，非对角线为0是"分散"。分散损失只保留了后者，即最小化特征维度之间的相关性。

这张表的核心信息是：分散损失这个概念是通用的，可以从多种对比学习框架中导出，其本质都是只保留"排斥/分散"项。

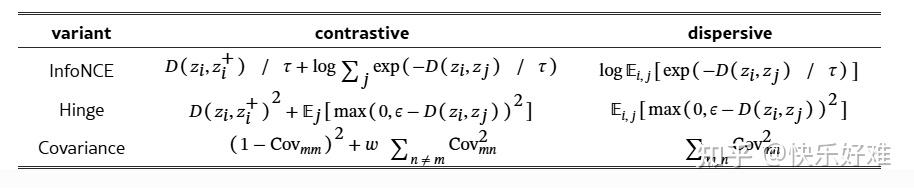
实验结果与分析

论文通过大量实验证明了分散损失的有效性和普适性。

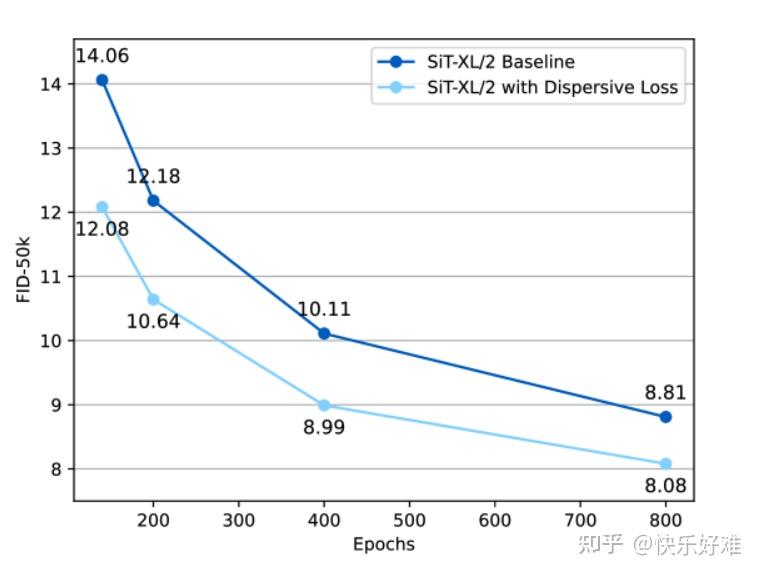
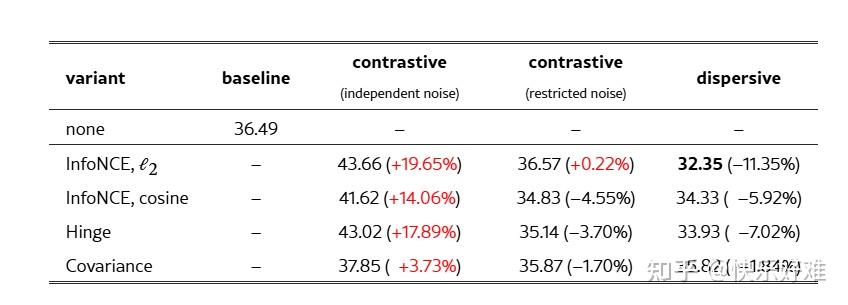
Figure 2 & Table 2: 分散损失 vs. 对比损失

Figure 2 : 这是一张效果速览图。FID分数越低，生成图像质量越好。可以看到，在整个训练过程中，加入了分散损失（橙线）的模型始终优于基线模型（蓝线）。
Table 2 : 这是最关键的对比实验之一。
- Baseline (基线): FID为36.49。
- Contrastive (对比损失): 如果直接引入标准的对比学习（需要为每个样本生成两个视图），效果并不好。特别是当两个视图的噪声独立采样时，性能甚至会严重下降（FID=43.66）。这说明在扩散模型中设计"正样本对"非常棘手。
- Dispersive (分散损失) : 简单地使用分散损失，效果却出奇地好。所有变体都带来了提升，其中基于L2距离的InfoNCE变体效果最好，将FID从36.49降低到32.35，相对提升了11.35%。

结论: 与其费力设计复杂的对比学习方案，不如用简单的分散损失，效果更好、更稳定。

Table 3 & Figure 3: 在哪一层施加损失？

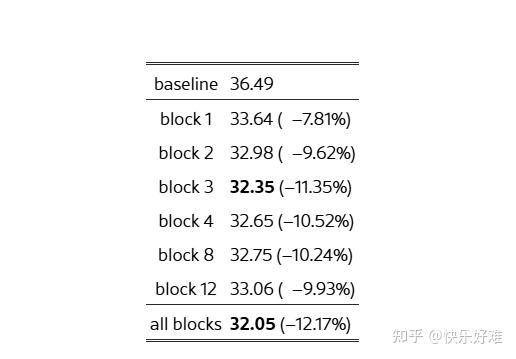
Table 3: 实验结果表明，在模型的**任何一个中间块（block）**施加分散损失，都能带来显著提升。施加在所有块上效果最好，但只在单个块（如第3块）上施加，效果也已经非常接近了。这说明该方法非常鲁棒。
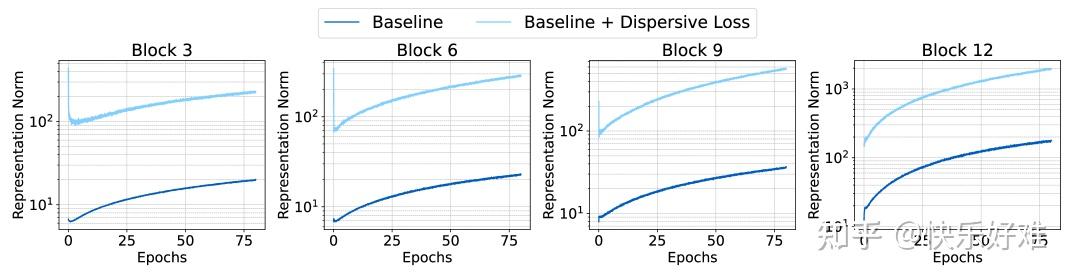
Figure 3 : 这张图揭示了背后的原因。当只在第3个块施加分散损失时（红线），不仅第3块的特征范数（norm）大幅增加，这种影响还传播到了模型的所有其他块 ，使得所有层的特征范数都比基线（蓝线）要高。这表明分散损失起到了一个全局的正则化作用，让整个模型的特征空间变得更"舒展"，从而避免了"表示坍塌"（representation collapse）。

Figure 4: 对不同模型和尺寸的普适性

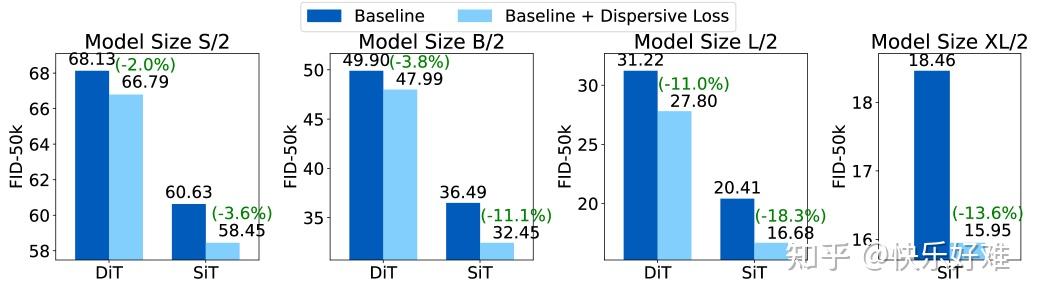
这张图展示了分散损失在不同模型（DiT, SiT）和不同尺寸（S, B, L, XL）上的效果。

结论: 在所有测试场景中，加入分散损失（橙色/红色条）都比基线（蓝色/绿色条）效果更好。
有趣的趋势 : 对于更强大的模型（如SiT vs. DiT，或L vs. S），分散损失带来的相对提升甚至更大 。这进一步印证了它的正则化作用------模型能力越强，越容易过拟合，因此也越能从有效的正则化中受益。

Table 5 & 6: 与SOTA方法的比较

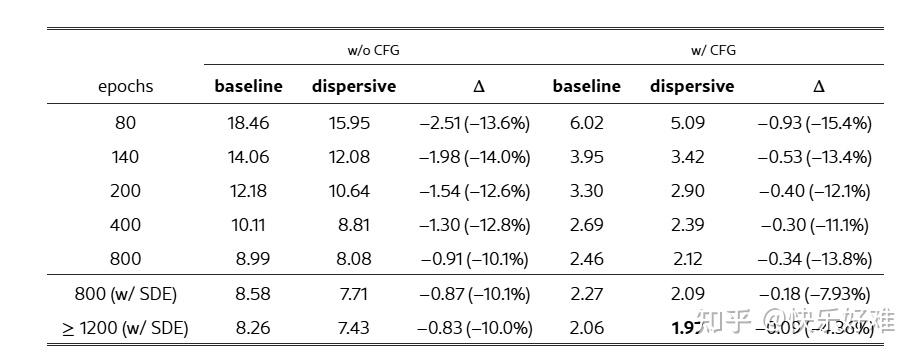
Table 5 : 作者在最强的SiT-XL模型上进行了充分的训练。结果显示，在各种训练设置下（长周期训练、使用CFG），分散损失都能稳定地带来10%~15%的相对性能提升，最终达到了1.97的FID分数（有CFG，SDE采样器）。

Table 6 : 这是与REPA的系统级对比。
- REPA : FID能达到1.80，数字上略胜一筹。但它的代价是：需要一个11亿参数 的外部模型（DINOv2），这个外部模型在1.42亿 张图片上进行了1500个epoch的预训练。
- Dispersive Loss : FID达到1.97，效果非常接近。但它的优势是：零预训练、零额外参数、零外部数据。

结论 : Dispersive Loss 提供了一条更简洁、高效、经济的路径来提升生成模型性能，证明了不依赖"外援"也能通过表示学习取得巨大进步。

Table 7: 在一步生成模型上的应用

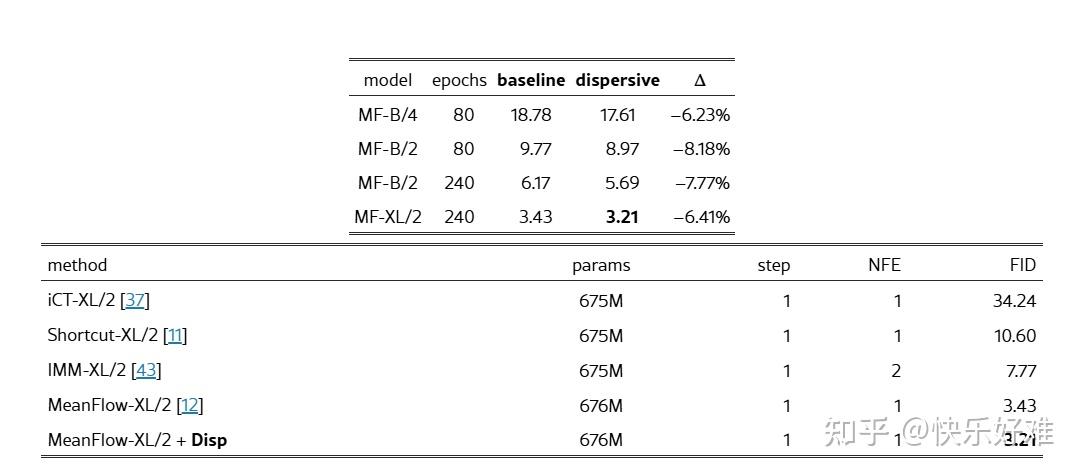
最后，作者将该方法应用到了最新的**一步生成模型MeanFlow**上。

左表: 在不同尺寸的MeanFlow模型上，分散损失都带来了稳定的性能提升。
右表 : 加上分散损失后，MeanFlow-XL/2的FID从3.43降至3.21 ，刷新了当时一步生成模型的SOTA纪录。

这证明了分散损失的普适性，它不仅适用于多步采样的扩散模型，也适用于对效率要求极高的一步生成模型。

总结

《Diffuse and Disperse》这篇论文提出了一个看似简单却蕴含深刻洞察的方法：

核心贡献 : 提出了分散损失 (Dispersive Loss)，一个即插即用、自给自足的正则化器，通过鼓励模型内部特征在空间中分散，来提升扩散模型的性能。
理论洞察: 它巧妙地将扩散模型的去噪任务视为隐式的"对齐"，从而将复杂的对比学习简化为只包含"排斥"项的"无正样本对比学习"。
实践价值:

效果显著: 在各种模型、尺寸和设置下都取得了稳定、可观的性能提升。
极简主义: 无需额外参数、预训练或外部数据，实现简单，开销极小。
普适性强: 不仅适用于传统扩散模型，还能提升SOTA的一步生成模型。

这篇工作为连接生成模型和表示学习这两个重要领域架起了一座优雅的桥梁，展示了通过内部表示正则化来提升生成模型的巨大潜力。

转自：论文速读：20250612 - 知乎