【微实验】弦振动 MATLAB 物理模型 动画仿真

谁敢想象，琴弦还可以这样像面条一样柔软地振动！

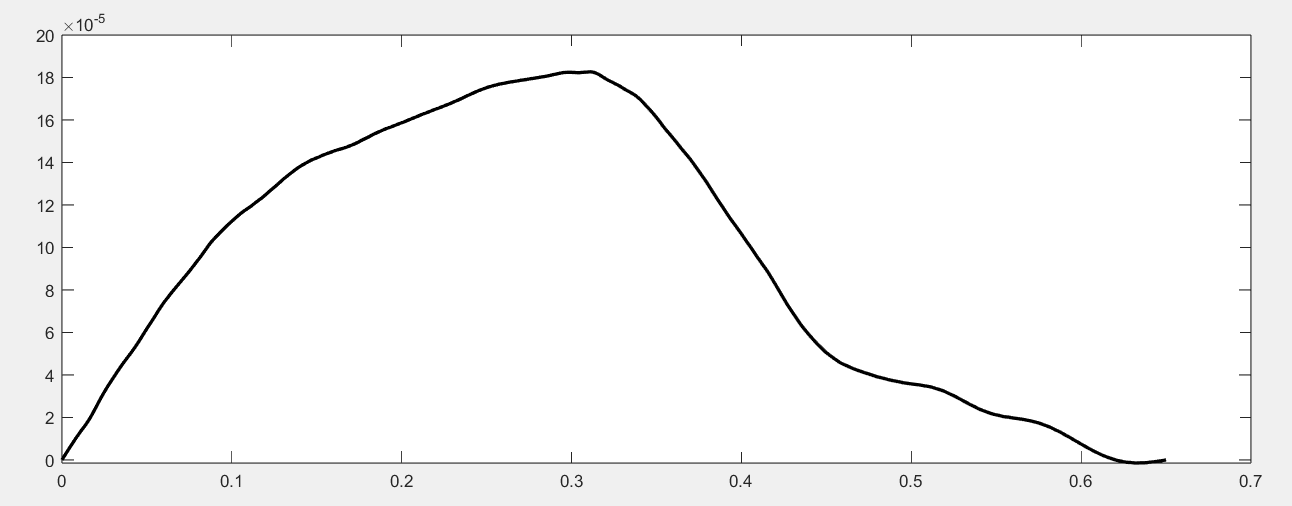
想必大家小学二年级学过，弦在被弹奏后，会产生除了基频之外的更高频振动模式。

网络上的科普也充斥着各个泛音振动模式的静态图，和百度百科这张大差不差。

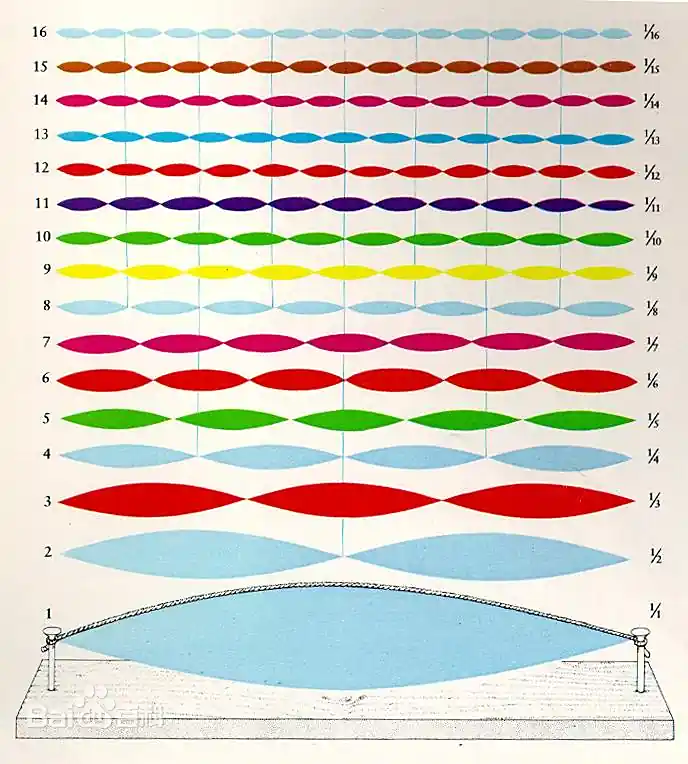
当然也有科普动画，不过大多是设定了一二三四五六七八九倍频的正弦波的振幅（甚至都没有调相位），然后放在一起振动，像疯了一样抽搐，产生的效果就是正弦波的叠加，看起来就假假的。

所以小编今天让AI帮忙，从物理的微分方程入手，编写了仿真代码。这个代码里，没有考虑琴弦的纵向向、扭转与倍频振动（若想了解，请参考：钢琴琴弦的振动方式 - 知乎），只考虑了通常认为是占比最大的横振动。

物理原理，请见这篇：波动方程------弦的横振动（牛顿第二定律+胡克定律）| 偏微分方程（二）_弦的波动方程-CSDN博客

还有这篇：

身边的微分方程 (4)：律动的琴弦

注意，这里仿真的是弹拨乐的琴弦（拉索乐器的持续性拉动在物理上相差很多）

借鉴了b站某位Up主的观点：琴弦在拨奏（敲击）的一瞬间

代码中设置了一些物理参数：

1. f0 (基频)

   • 默认值：440Hz（标准 A4 音高）
   • 调节范围：27.5Hz（钢琴最低音）至 4186Hz（钢琴最高音）
   • 影响：直接决定琴弦发出的音高，改变此值会改变整个频谱特性

2. L (弦长)

   • 默认值：0.65 米（钢琴 A4 弦典型长度）
   • 调节范围：0.05 米至 2 米
   • 影响：弦长增加会降低基频，符合弦乐器 "长弦低音" 的物理规律

3. T (弦张力)

   • 默认值：700 牛顿（钢琴弦典型张力）
   • 调节范围：100N 至 2000N
   • 影响：张力增加会提高波速和基频，同时改变振动模式

4. rho (线密度)

   • 默认值：0.0006 kg/m（钢琴钢丝典型密度）
   • 调节范围：0.0001 至 0.01 kg/m
   • 影响：线密度增加会降低波速和基频，模拟不同粗细的琴弦

还有一些振动初始状态相关的参数：

1. y0 (最大初始位移)

   • 默认值：0.015 米
   • 调节范围：0.001 至 0.1 米
   • 影响：决定振动的初始幅度，值越大振动越明显
   • 建议：值过大会导致非线性效应，建议保持在 0.001-0.05 米范围

2. strike_pos (琴槌击弦位置)

   • 默认值：0.2（弦长的 20% 处）
   • 调节范围：0.05 至 0.95
   • 影响：改变击弦点位置会影响振动模式和谐波分布
   • 建议：尝试 0.1/0.25/0.5 等不同位置，观察音色变化

3. strike_width (击弦接触宽度)

   • 默认值：0.1（弦长的 10%）
   • 调节范围：0.01 至 0.5
   • 影响：模拟琴槌与弦的接触面积，影响初始振动能量分布
   • 建议：值越小模拟点接触，值越大模拟面接触

剩余的是关于仿真动画设置的参数，下面的代码中在笔者电脑上运行能够得到比较好的动画效果，笔者自己也没调明白，感兴趣的友友可以把代码复制运行自行调节。

实验版代码如下：

% 琴弦振动仿真
% 功能：模拟指定频率的琴弦振动过程，慢放显示

% 清除工作区变量、命令行窗口内容，关闭所有图形窗口
clear; 
clc; 
close all;  

% 1. 物理参数设置（基于A4音弦特性）
f0 = 440;              % 琴弦基频（Hz），对应钢琴A4音
L = 0.65;              % 弦长（米），参考钢琴A4弦实际长度
T = 700;               % 弦张力（牛顿），影响波速
rho = 0.0006;          % 线密度（kg/m），单位长度的质量
c = sqrt(T/rho);       % 波速（m/s），由张力和线密度决定

% 2. 仿真参数设置（优化显示效果）
slow_factor = 4;      % 慢放因子，数值越小放得越慢 
fps = 30;              % 动画帧率（帧/秒）
total_time = 5;        % 仿真振动持续时间（秒）
sim_time = total_time * slow_factor;  % 仿真显示总时间（秒）
num_frames = sim_time * fps;          % 总帧数

% 3. 空间离散化设置
Nx = 400;              % 空间网格点数，越多曲线越平滑
x = linspace(0, L, Nx);  % 弦上各点的位置坐标（米）
dx = x(2) - x(1);       % 空间步长（米）

% 4. 时间离散化设置（关键：确保数值稳定性）
% 根据Courant条件计算最大稳定时间步长（避免数值发散）
dt_max = 0.5 * dx / c;  % 最大允许时间步长
% 实际时间步长取较小值（确保稳定）
dt_actual = min(1/(fps*slow_factor), dt_max);
Nt = total_time / dt_actual;  % 总时间步数

% 5. 初始化弦的位移状态
y = zeros(1, Nx);       % 当前时刻的位移数组
y0 = 0.015;              % 最大初始位移（米），影响振动幅度
strike_pos = 0.2;      % 琴槌击弦位置（弦长的20%处）
strike_width = 0.1;     % 击弦接触宽度（弦长的10%）

% 计算击弦位置的索引
strike_idx = find(x >= strike_pos, 1);
% 计算接触区域的左右边界索引
left_idx = max(1, strike_idx - round(strike_width/dx/2));
right_idx = min(Nx, strike_idx + round(strike_width/dx/2));

% 用傅里叶级数叠加生成三角波（模拟琴槌击弦）
% 三角波傅里叶级数：y(x) = (8y0/π²)Σ[sin((2k-1)πx/L)/(2k-1)²]
n_harmonics = 20;       % 傅里叶级数项数（控制精度）
y_tri = zeros(1, Nx);   % 三角波形数组

for k = 1:n_harmonics
    % 奇次谐波叠加（三角波的傅里叶特性）
    harmonic = (2*k - 1);
    % 傅里叶级数公式
    y_tri = y_tri + (8*y0/(pi^2)) * ...
        sin(harmonic*pi*x/L) / (harmonic^2);
end

% 仅在击弦区域保留位移，其他区域衰减为0（模拟局部击弦）
decay = zeros(1, Nx);
% 击弦区域内保持100%振幅
decay(left_idx:right_idx) = 1;
% 左侧区域线性衰减
if left_idx > 1
    decay(1:left_idx-1) = linspace(0, 1, left_idx-1);
end
% 右侧区域线性衰减
if right_idx < Nx
    decay(right_idx+1:end) = linspace(1, 0, Nx-right_idx);
end

% 应用衰减后的三角波作为初始位移
y = y_tri .* decay;

% 确保边界条件（两端位移严格为0）
y(1) = 0;
y(end) = 0;

y_prev = y;            % 上一时刻的位移（用于差分计算）
y_next = zeros(1, Nx); % 下一时刻的位移（计算结果存储）

% 6. 创建可视化窗口
% 设置窗口位置和大小
fig = figure('Position', [200 200 1000 500]);
% 确保窗口前置可见
set(fig, 'WindowState', 'normal');  
% 设置坐标轴范围
axis([0 L -1.5*y0 1.5*y0]);
xlabel('弦位置 (m)');      % x轴标签
ylabel('位移 (m)');        % y轴标签
title('440Hz琴弦振动仿真（1000倍慢放）');  % 标题
grid off;                  % 不显示网格
hold on;                  % 保持当前绘图，后续可叠加

% 7. 初始绘制
% 绘制琴弦散点
scatter_handle = plot(x, y, 'k-', 'MarkerSize', 3, 'LineWidth', 2);
% 添加时间显示文本
time_text = text(0.05, 0.9*y0, sprintf('时间: 0.00s (实际: 0.0000s)'));

% 8. 振动仿真与实时更新
% 添加阻尼系数（模拟能量损耗，使振动更真实）
damping_factor = 0.995; %理论上讲是要小于等于1，否则弦会越振越剧烈。 
%经过实际调参，这个后面小数位数越多，震动就越慢？
%甚至在显示界面晃动鼠标都会让动画变慢......救命，不会调了

% 时间迭代计算（核心循环）
for i = 1:Nt
    % 有限差分法求解波动方程
    % 计算内部点的位移（j=2到Nx-1，避开边界）
    for j = 2:Nx-1
        % 波动方程的差分格式：y_next = 2y - y_prev + (c²Δt²/Δx²)(y(j+1)-2y(j)+y(j-1))
        y_next(j) = 2*y(j) - y_prev(j) + ...
            (c^2 * dt_actual^2 / dx^2) * (y(j+1) - 2*y(j) + y(j-1));
    end
    
    % 固定边界条件（弦两端固定不动）
    y_next(1) = 0;       % 左端位移始终为0
    y_next(end) = 0;     % 右端位移始终为0
    
    % 应用阻尼效应（模拟能量衰减）
    y_next = y_next * damping_factor;
    
    % 检查是否产生NaN值（数值不稳定的标志）
    if any(isnan(y_next(:)))
        warning('计算过程中出现NaN值，可能是数值不稳定导致');
        break;  % 提前终止循环
    end
    
    % 更新位移状态（为下一迭代做准备）
    y_prev = y;      % 当前位移变为"上一时刻"位移
    y = y_next;      % 计算得到的位移变为"当前时刻"位移
    
    % 每slow_factor步更新一次图形（控制动画速度）
    if mod(i, slow_factor) == 0
        frame_idx = i / slow_factor;  % 当前帧索引
        
        % 更新图形：先删除旧图，再绘制新图
        delete(scatter_handle);
        scatter_handle = plot(x, y, 'k-', 'MarkerSize', 3, 'LineWidth', 2);
        
        % 更新时间显示文本
        set(time_text, 'String', sprintf('时间: %.2fs (实际: %.4fs)', ...
            frame_idx/fps, i*dt_actual));
        
        drawnow;  % 强制刷新图形窗口
        pause(0.01);  % 这里可以调节延迟，便于观察
        
        % 达到预设帧数后停止
        if frame_idx >= num_frames
            break;
        end
    end
end

% 仿真结束提示
fprintf('仿真结束！\n');

累了，让AI帮忙总结一下------

实验调节建议与探索方向：

1. 音色探索实验

   • 改变击弦位置 (strike_pos)：尝试 0.1/0.25/0.5 不同位置，观察振动模式变化
   • 调整击弦宽度 (strike_width)：从 0.05 到 0.2，观察初始振动能量分布变化

2. 弦特性实验

   • 改变弦长 (L)：从 0.3 米到 1 米，观察基频变化
   • 调整张力 (T)：从 300N 到 1000N，观察波速和振动模式变化

3. 阻尼效应实验

   • 尝试不同阻尼系数：0.999/0.995/0.99，观察振动衰减特性
   • 比较不同材质琴弦：修改 rho 值模拟不同密度的弦材料

4. 慢放效果实验

   • 调整 slow_factor：从 1 到 1000，体验不同慢放倍数下的视觉效果
   • 改变 fps：从 15 到 60，观察动画流畅度与计算效率的平衡

---

注意事项：

1. 数值稳定性：当出现 NaN 值时，通常是因为时间步长过大或初始位移设置不合理，可尝试减小 y0 或增加 Nx
2. 计算性能：高 Nx 值和低 slow_factor 会显著增加计算量，建议根据电脑性能调整
3. 边界条件：确保弦两端位移始终为 0，这是物理模拟的基础条件
4. 视觉效果：可通过修改 plot 函数的颜色和线型参数，定制个性化的视觉效果

另外不要中途关闭动画窗口，否则会报错，然后过一会蹦出来一个大小奇怪的窗口和抽搐的琴弦------

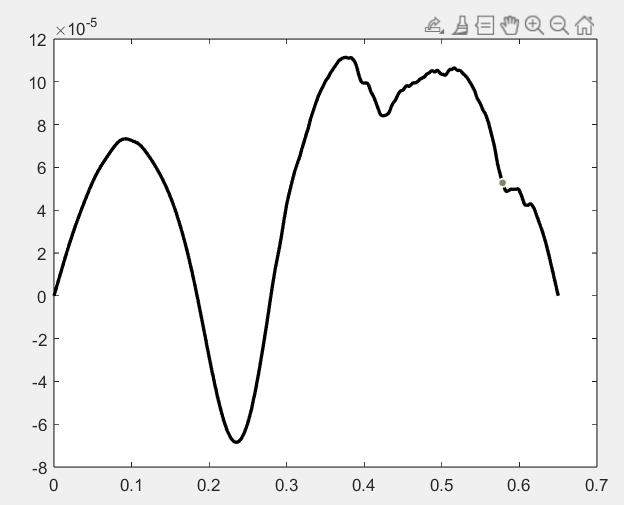
通过这个实验，我们不仅能直观理解琴弦振动的物理过程，还能深入探索不同参数对振动效果的影响，为声学研究和乐器设计提供理论支持。

就这样吧。感谢每一位看到这里的大佬，如果能在评论区交流一下看法或者指出一些问题，笔者将不胜感激（ - 人 - ）