【数据结构入门】堆

1.堆的概念

2.堆的实现（小堆）

[2.1 堆的结构体](#2.1 堆的结构体)

[2.2 堆的初始化&建堆（逻辑）](#2.2 堆的初始化&建堆（逻辑）)

[2.3 建堆（物理数组）](#2.3 建堆（物理数组）)

[2.3.1 向下调整算法](#2.3.1 向下调整算法)

[2.3.2 满足向下调整算法的条件](#2.3.2 满足向下调整算法的条件)

[2.3.3 建堆的时间复杂度分析](#2.3.3 建堆的时间复杂度分析)

[2.4 堆排序](#2.4 堆排序)

1.堆的概念

堆本质上是完全二叉树 使用数组存储的一个数据结构。

堆分为大根堆、小根堆：

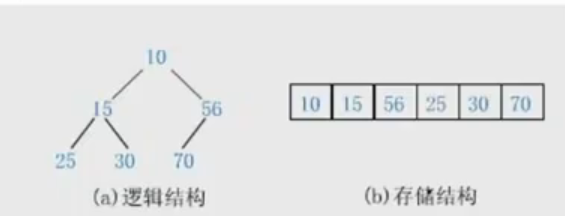
大根堆：

每个父亲结点都大于等于孩子结点。

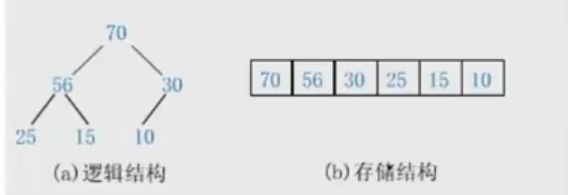
小根堆：

每个父亲结点都小于等于孩子结点。

堆可以用来选出这个堆中最大或者最小的值，只需要不断维护这个堆即可，那么后面的堆排序的原理其实就是通过维护堆来实现的。

我们做一下下面的题目，巩固一下堆的概念：

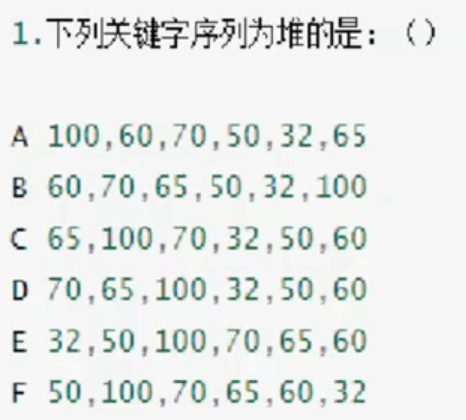
可以直接还原为完全二叉树，也可以目测，首先判断第一个数和第二个数的大小，如果第一个数大于第二个数那么就是大根堆，如果后面的数字有比第一个数字大的直接排除，小根堆同理，选A。

2.堆的实现（小堆）

2.1 堆的结构体

这里使用数组实现，由于后续可能考虑到堆的插入会涉及到扩容的问题，所以这里需要一个size表示实际的元素个数，以及capacity堆的容量。

cpp 复制代码

typedef int dataType;
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct Heap
{
	dataType* data;
	int size;
	int capacity;
}Heap;

2.2 堆的初始化&建堆（逻辑）

对于堆中的data来说，需要创建一个固定大小的空间，此时外界传入空间的大小，大小赋给size和capacity，需要注意的一点是，第一次建堆的时候，数据是从外界获取的，可以是在数组开辟完毕之后拷贝过来。

cpp 复制代码

void heapInit(Heap* p, dataType* data, int size) 
{
	p->data = (dataType*)malloc(sizeof(dataType)*size);
	memcpy(p->data,data, sizeof(dataType) * size);// 提供的数组数据拷贝到堆内数组
	p->size = size;
	p->capacity = size;
	
	// 建堆
}

接下来就要开始建堆了，假如外界传入一组数据，我们如何构建小堆呢？

这里举一个非常特殊的例子，当一个完全二叉树的根结点的左右子树都是小堆，只有根结点需要进行调整，那么我们调整的过程如下：

①27首先和自己的左右孩子进行比较，选出最小的孩子和自己交换，即27和15交换。

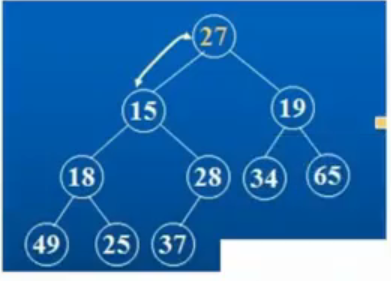
②接下来，只需要调整左子树即可，因为右子树本身就是一个小堆，我们需要找出27的左右孩子中较小的那一个进行交换，也就是和18进行交换。

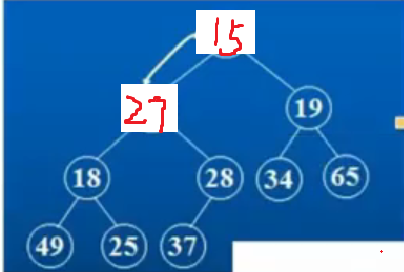
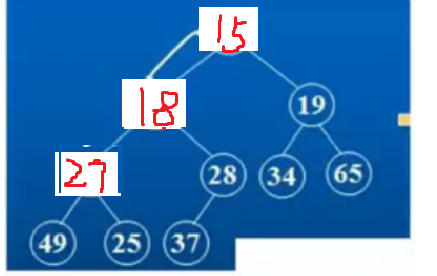
③最后选出25和27交换，最终形成了小根堆。

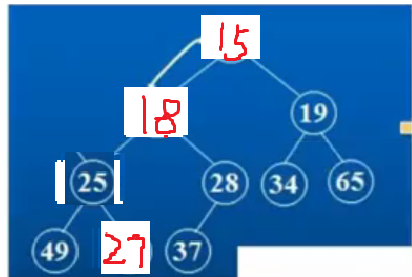
上面调整的过程就是所谓的向下调整算法，这个算法的前提是左右子树都是小堆（大堆）。

2.3 建堆（物理数组）

①首先需要找到根结点的左右孩子，其实就是根节点的下标*2+1（左孩子），根节点的下标*2+2（右孩子）。

②找到左右孩子之后，需要判断自己是否是小堆，即自己是否比孩子要小，如果不是需要和孩子交换。

③选出孩子中较小的一个进行交换，交换完毕之后，新的根结点就是那个被交换的孩子，以此类推继续判断自己是不是小堆。

④每次计算孩子下标的时候，需要判断下标是否越界，如果越界说明，本节点就是叶子结点。

2.3.1 向下调整算法

首先函数需要三个参数，第一个是需要调整的堆，第二个是堆中数组的长度，第三个是指定需要调整的堆的根结点的下标。

然后我们假设根结点的左孩子是最小的孩子，如果判断右孩子比左孩子还小，那么更新右孩子为左孩子。

其次，若根节点比最小的孩子还要大，那么就进行交换，交换完毕之后需要更新最新的根结点是最小的孩子，同时需要计算最新的孩子。

最后，我们发现这个过程是一个持续的过程，所以写成循环，退出循环的条件是当孩子节点计算的值大于或等于数组的长度，说明这个结点就是叶子结点需要终止循环；

然而我们发现循环还是有问题，因为只有头结点交换了才会更新头结点和孩子节点的下标，这样就永远无法退出循环，所以如果没有发生交换，也就是说头结点本身比最小的孩子节点还要小，说明就不需要进行堆调整了，直接退出循环。

cpp 复制代码

void Swap(dataType* p1, dataType* p2)
{
	dataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 向下调整算法，默认左右子树都是小堆
void adjustDown(dataType* a, int n,int root)// 堆，数组长度，需要调整的根结点
{
	// 选出最小的孩子
	int parent = root;
	// 最小孩子下标
	int childIndex = 2 * parent + 1;// 默认左孩子是最小的孩子
	while (childIndex < n ) //左右孩子都不能越界
	{
		// 右孩子更小，那么就调整最小孩子的下标为右孩子
		if ( childIndex + 1 < n && a[childIndex] > a[childIndex + 1])
		{
			++childIndex;
		}
		if (a[parent] > a[childIndex]) // 父结点比子结点大，不是小堆，需要交换
		{
			Swap(&a[parent], &a[childIndex]);
			parent = childIndex;
			childIndex = 2 * parent + 1;
		}
		else 
		{
			// 小的孩子已经大于父亲，直接退出循环即可
			break;
		}
	}
}

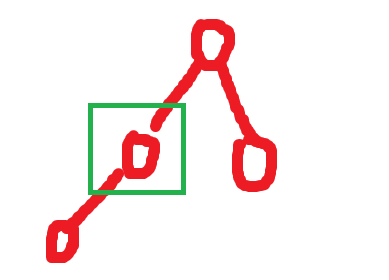
BUG：仔细阅读代码会发现，这个代码存在越界问题，若当前根节点是绿色方框框选的结点，那么我们势必要访问它的孩子节点，此时循环判断左孩子节点（默认最小孩子赋值为左孩子）的下标小于n，但是要访问它的右孩子一定会发生越界的问题，我们该如何处理呢？

cpp 复制代码

while (childIndex < n)
{
// 右孩子更小，那么就调整最小孩子的下标为右孩子
		if (a[childIndex] > a[childIndex + 1])
		{
			++childIndex;
		}
......
}

这里只有一个左孩子，根结点还是需要和左孩子交换的，所以只需要在判断语句中判断，如果右节点的下标小于数组长度并且右节点小于左节点，才能更新最小孩子节点为右节点。

cpp 复制代码

while (childIndex < n ) //左右孩子都不能越界
{
	// 右孩子更小，那么就调整最小孩子的下标为右孩子
	if ( childIndex + 1 < n && a[childIndex] > a[childIndex + 1])
	{
		++childIndex;
	}
    .......
}

到了这里还是有一个致命的问题，我们无法保证传过来的根结点的左右子树都是小堆，这个条件太苛刻了，如果不满足这个条件，就无法使用向下调整算法。

2.3.2 满足向下调整算法的条件

已知每一个单独的叶子节点都可以看做一个堆，那么我们只需要从叶子结点所处的最小二叉树入手，即找到叶子结点的父结点，(下标-1)/2即可；

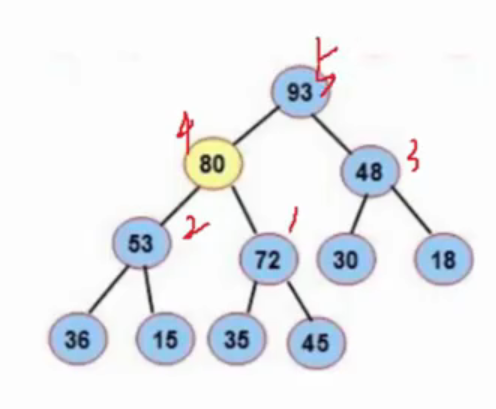
找到父结点之后，例如下图的72，由于两个叶子结点都是单独的节点也就是单独的堆，是满足向下调整算法的条件的，那么我们只需要将72作为根节点进行向下调整算法，使其变成一个堆，以此类推，调完72之后，再去调它的兄弟节点53，只需要下标-1即可，两个子树都符合向下调整的算法，53所在的子树调整完毕之后，下标继续-1，就是48所在的子树进行调整。

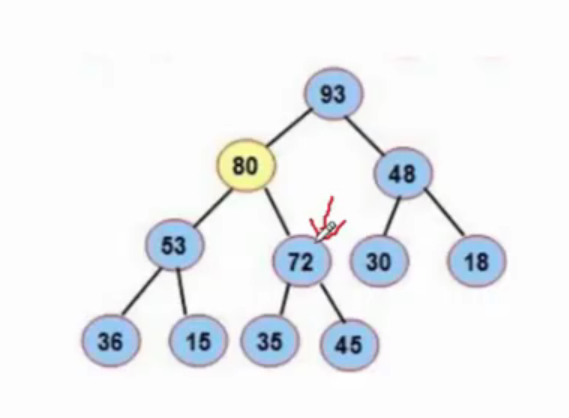
调整的顺序如下：

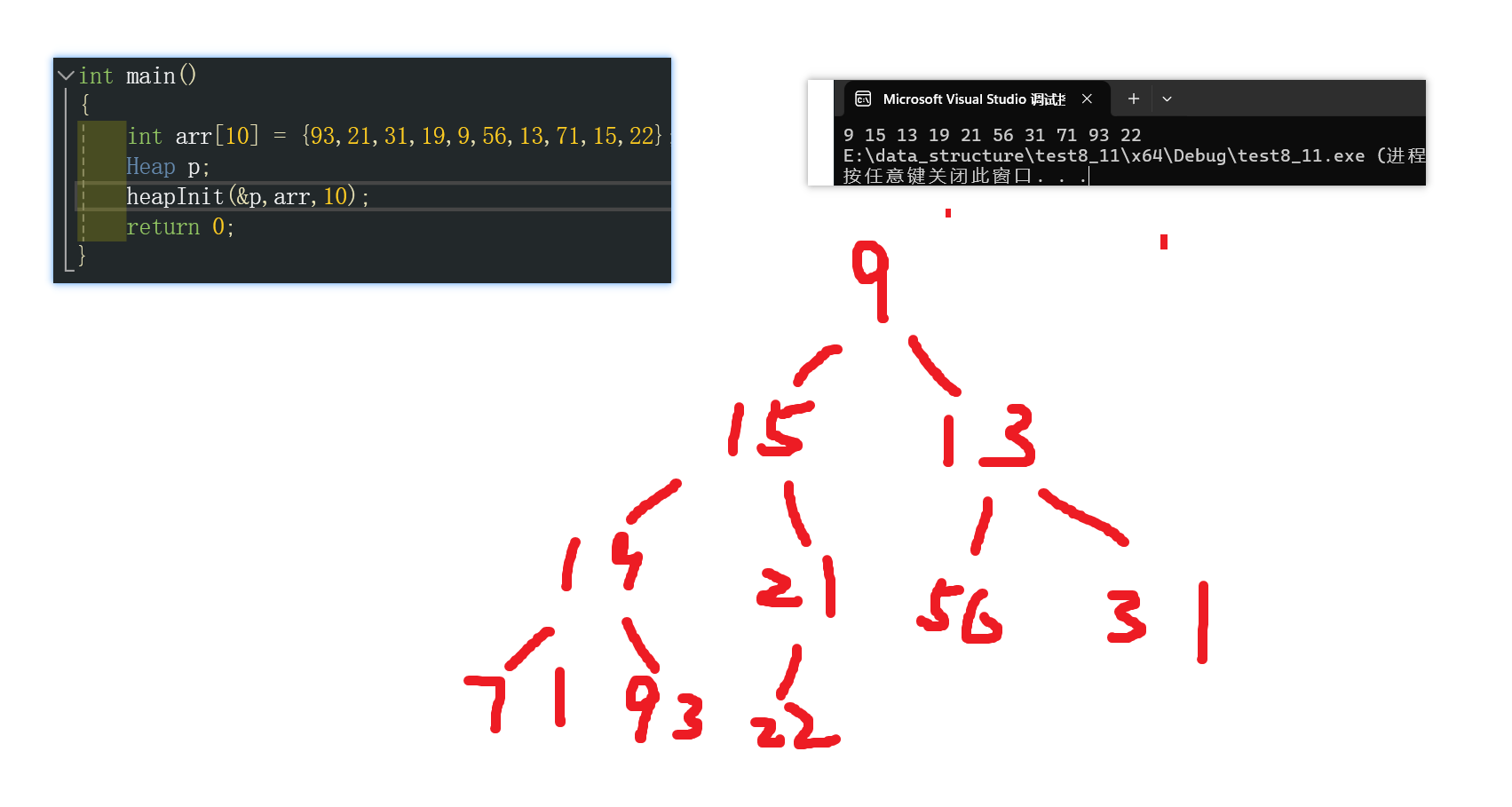
所以堆的初始化已经完成，这里可以打印数组看看。

cpp 复制代码

// 堆初始化
void heapInit(Heap* p, dataType* data, int size)
{
	p->data = (dataType*)malloc(sizeof(dataType) * size);
	memcpy(p->data, data, sizeof(dataType) * size);// 提供的数组数据拷贝到堆内数组
	p->size = size;
	p->capacity = size;

	// 建堆
	// 最后一个叶子结点的下标是size - 1,找父亲节点就是，(孩子节点-1)/2
	for (int i = (size-1-1)/2; i >= 0; --i)
	{
		adjustDown(p->data,p->size,i); // 最后一个叶子节点的父结点开始每次下标-1，依次进行向下调整
	}
}

将调整后的数组直接打印，发现能够正常输出小堆。

2.3.3 建堆的时间复杂度分析

树的高度是，那么最坏情况是要遍历整个堆，一共调整的次数是N/2次，所以可能读者会认为建堆的过程的时间复杂度是，但是实际上并不是这样。

cpp 复制代码

for (int i = (size-1-1)/2; i >= 0; --i)
{
	adjustDown(p->data,p->size,i); // 最后一个叶子节点的父结点开始每次下标-1，依次进行向下调整
}

因为我们的调整是从堆的最后一个节点的父结点 开始的，如果是下标是从0开始那么时间复杂度才是。

我们假设是一个满二叉树，高度是h，那么：

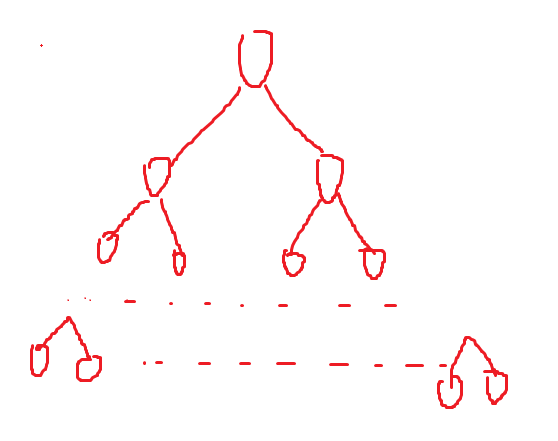
头结点一共有个节点，每一个节点需要向下调整h次；

第二层一共有个节点，每一个节点需要向下调整h-1次；

......

最后一层一共有个节点，每一个节点需要向下调整0次；

那么总的调整次数是：

又因为满二叉的高度满足：

带入得：

化简得：

得出时间复杂度是O(N)。

2.4 堆排序

学会向下调整、建堆之后，我们就可以尝试完成堆排序了。

①建堆，选出最小的数。

②有的读者可能觉得接下来要选出次小的数，需要继续建堆，如此一来，每次选择一个数都要建堆，一共有n个数，那么时间复杂度就来到了n的平方，此时堆排序就毫无优势了。

③第一次建堆选出最小的数，这个数和数组最后一个数进行交换，将数组的长度-1，不参与后面的排序。

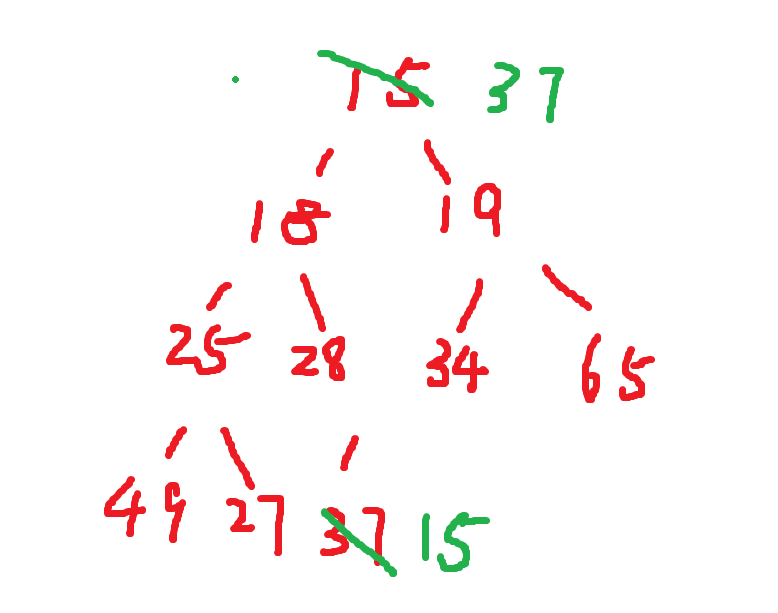
④将最后一个元素剔除之后，满足向下调整算法，这里进行向下调整算法，选出次小的数，和现在的最后一个数进行交换，再将数组长度-1，使其不参与后面的运算，以此类推......

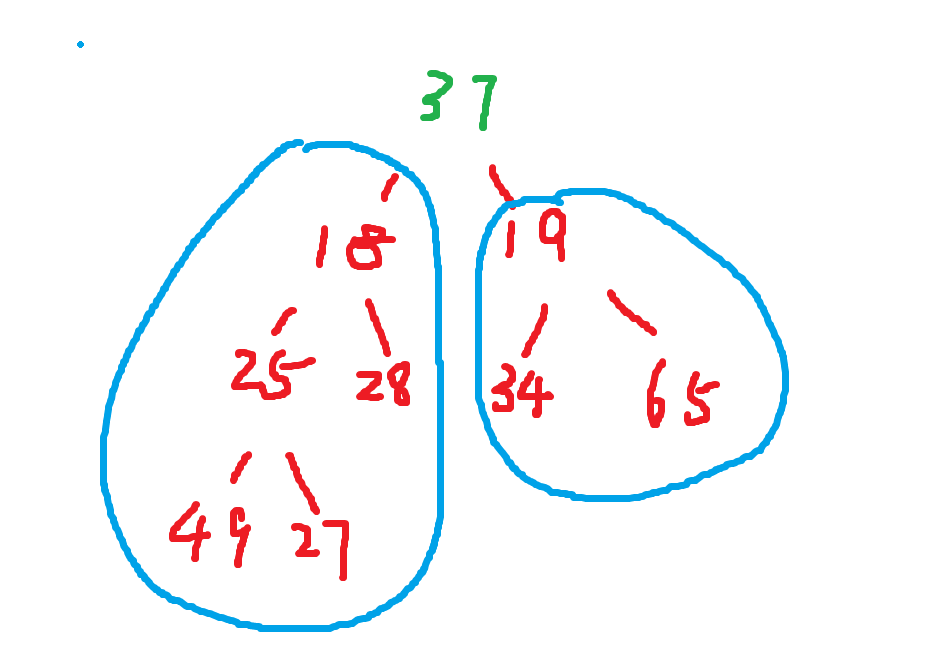
⑤此时的时间复杂度可以计算了，每次向下调整h，有n个数需要调整那么堆排序的时间复杂度是

比之前的N平方小了不少。

除此之外我们可以得出一个结论：建小堆->降序排序，建大堆->升序排序。

堆排序的流程：

1.首先建小堆，首元素就是最小的元素。

2.此时将这个元素放到数组最后，此时再进行向下调整算法，这里需要注意的是传入end，是数组的长度而不是下标，这里将end传入其实就是将下标0-end-1的数组进行向下调整算法，选出次小值。

3.调整完毕缩小右边界，下一次交换直接在新的最后一个元素上。

4.end是最后一个元素的下标，那么end到0的时候其实就是，自己和自己交换、向下调整，所以end=0没有必要。

cpp 复制代码

void heapSort(int* a1, int n)
{
	int arr[10] = { 93,21,31,19,9,56,13,71,15,22 };
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		adjustDown(arr, n, i);
	}
	// 定义数组最后一个数
	int end = n - 1;
	while (end > 0)
	{
		// 小堆的堆顶和"最后一个数"交换
		Swap(&arr[0],&arr[end]);
		adjustDown(arr,end,0);// 注意这里的end代表的是数组的长度，下标取值是end-1
		--end;// 缩小右边界
	}
}