目录

1.摘要
本文提出了一种面向无人机(UAV)新型轨迹优化方法,以实现对地面移动节点的高效视觉覆盖。与传统方法不同,该方法显式考虑节点的移动性,生成连续且平滑的三维飞行轨迹,更符合实际应用需求。研究目标是通过优化无人机轨迹设计,最大化任务执行过程中被覆盖的节点总数。为降低无限解空间带来的计算复杂度,本文首先利用 Bézier 曲线将连续的轨迹优化问题转化为离散的控制点选择问题,在保证轨迹平滑性的同时大幅简化计算。随后,基于矩阵差分进化算法(MDE)框架,提出了一种无人机轨迹优化算法,有效兼顾覆盖性能与计算效率。
2.系统模型和问题表述
网络模型
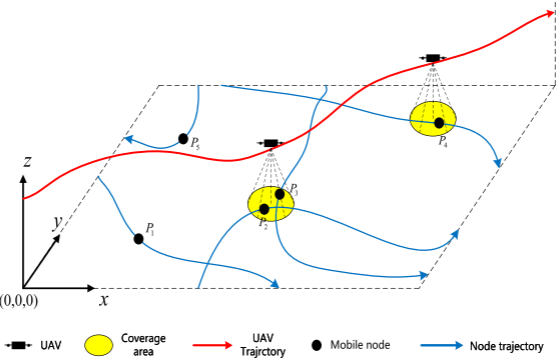
本文研究旋翼式无人机在二维平面上执行地面移动节点的视觉覆盖任务。设平面内共有 n n n个移动节点,每个节点均以一定速度沿各自的预设轨迹独立运行。忽略节点间碰撞,第 i i i个节点记为 P i P_i Pi,轨迹长度为 L i L_i Li:
Q = { q i ( t ) ∣ i ∈ [ 1 , n ] , 0 ≤ t ≤ T m a x e } \mathbf{Q}=\{\mathbf{q}{i}(t)|i\in[1,n],0\leq t\leq T{\mathrm{max}}^{e}\} Q={qi(t)∣i∈[1,n],0≤t≤Tmaxe}
V = { v i ∣ i ∈ [ 1 , n ] } \mathbf{V}=\{v_{i}|i\in[1,n]\} V={vi∣i∈[1,n]}
每个地面节点虽速度各异,但在运动过程中均保持恒定。无人机搭载圆形视觉传感器,从初始点 ( 0 , 0 , H u ) (0,0,H_u) (0,0,Hu)起飞,以固定高度 H u H_u Hu沿平滑连续的轨迹飞行,最终抵达终点 ( E x , E y , H u ) (E_x,E_y,H_u) (Ex,Ey,Hu)完成覆盖任务。
视觉覆盖模型
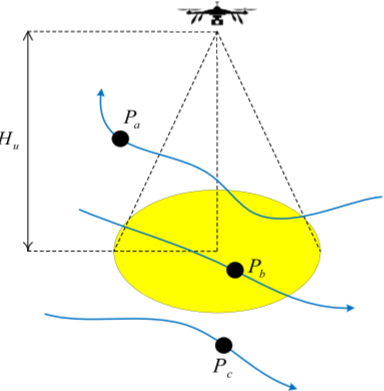
模型将节点简化为沿轨迹运动的点目标,忽略其形状与尺寸。为保证监测质量,每个节点需满足最低分辨率要求。无人机采用定焦视觉传感器,其分辨率与飞行高度成反比:高度越高,覆盖范围越大但分辨率下降。为兼顾覆盖与能耗,无人机飞行高度取所有节点允许高度的最小值,并据此确定视场半径。
问题描述
本文研究目标是确定一条最优无人机飞行规划 q ∗ \mathbf{q}^{*} q∗,在一定约束条件下,使无人机视觉覆盖的地面移动节点数量最大化。在任务执行时间内共覆盖 S S S个地面易懂节点:
S = ∑ i = 1 n S i S=\sum_{i=1}^nS_i S=i=1∑nSi
优化目标可表述为:
q ∗ = arg max T ≤ T c s ≤ T m a x e S \mathbf{q}^*=\arg\max_{T\leq T_{cs}\leq T_{\mathrm{max}}^e}S q∗=argT≤Tcs≤TmaxemaxS
限制无人机在三维空间 Ω \Omega Ω内运动:
Ω = { v = ( x , y , z ) ∈ R 3 0 ≤ x ≤ E x , 0 ≤ y ≤ E y , 0 ≤ z ≤ H u } \Omega= \begin{Bmatrix} v=(x,y,z)\in\mathbb{R}^3 & 0\leq x\leq E_x, & 0\leq y\leq E_y, & 0\leq z\leq H_u \end{Bmatrix} Ω={v=(x,y,z)∈R30≤x≤Ex,0≤y≤Ey,0≤z≤Hu}
3.矩阵差分进化算法
由于优化问题为非凸难以实时求解,本文提出基于矩阵差分进化算法(MDE)框架,该方法在DE的基础上,引入矩阵化候选解表示与参数更新机制,便于并行计算与协同优化,其核心流程包括初始化、变异、交叉与选择四个步骤。
将控制点坐标向量化,上下界:
U = [ E x , E y , E x , E y , ⋯ , E x , E y ] \mathbf{U}= \begin{bmatrix} E_x,E_y,E_x,E_y,\cdots,E_x,E_y \end{bmatrix} U=[Ex,Ey,Ex,Ey,⋯,Ex,Ey]
L = [ 0 , 0 , 0 , 0 , ⋯ , 0 , 0 ] \mathbf{L}=[0,0,0,0,\cdots,0,0] L=[0,0,0,0,⋯,0,0]
种群变异
本文采用DE/rand/1方式,比例因子在MDE中用矩阵表述:
Λ = λ F N × D \Lambda=\lambda\mathbf{F}_{N\times D} Λ=λFN×D
构造供体矩阵为:
Y g = X [ r 1 , ⋅ ] g + Λ ∘ ( X [ r 2 , ⋅ ] g − X [ r 3 , ⋅ ] g ) \mathbf{Y}^{g}=\mathbf{X}{[\mathbf{r}{1},\cdot]}^{g}+\mathbf{\Lambda}\circ\left(\mathbf{X}{[\mathbf{r}{2},\cdot]}^{g}-\mathbf{X}{[\mathbf{r}{3},\cdot]}^{g}\right) Yg=X[r1,⋅]g+Λ∘(X[r2,⋅]g−X[r3,⋅]g)
种群交叉
交叉算子主要参数是交叉率,比例因子:
Γ = γ F N × D \Gamma=\gamma\mathbf{F}_{N\times D} Γ=γFN×D
控制点种群矩阵:
W g = Y g ∘ Φ + X g ∘ Φ ‾ \mathbf{W}^{g}=\mathbf{Y}^{g}\circ\mathbf{\Phi}+\mathbf{X}^{g}\circ\mathbf{\overline{\Phi}} Wg=Yg∘Φ+Xg∘Φ
种群选择
定义适应度函数 f i t : R N × D → R N × 1 fit:\mathbb{R}^{N\times D}\to\mathbb{R}^{N\times1} fit:RN×D→RN×1,贪心保留种群。新一代种群生成:
X g + 1 = W g ∘ ( B z × F 1 × D ) + X g ∘ ( B z ‾ × F 1 × D ) X^{g+1}=W^g\circ(B_z\times F_{1\times D})+X^g\circ(\overline{B_z}\times F_{1\times D}) Xg+1=Wg∘(Bz×F1×D)+Xg∘(Bz×F1×D)

4.结果展示
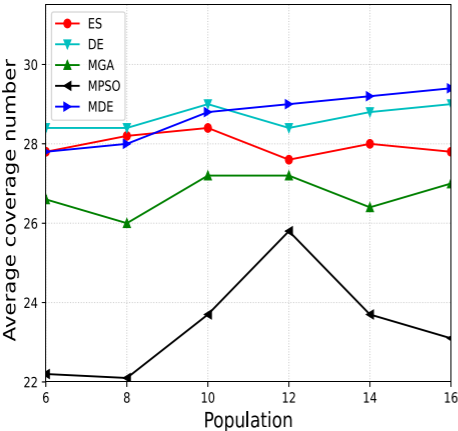
5.参考文献
1\] Jia R, Li H, Sun P, et al. UAV trajectory optimization for visual coverage in mobile networks using matrix-based differential evolution\[J\]. Knowledge-Based Systems, 2025: 113797. ### 6.算法辅导·应用定制·读者交流 xx