算法题打卡力扣第169题：多数元素(easy)

文章目录

• • 题目描述
  • 解法一：暴力解
  • [解法二 排序法](#解法二 排序法)
  • [解法三：Boyer-Moore 投票算法 (最优解)](#解法三：Boyer-Moore 投票算法 (最优解))

题目描述

解法一：暴力解

定义一个数组C用于存放nums数组中每个数出现的次数，然后再遍历C，判断C【i】是否大于⌊ n/2 ⌋，如果是，则返回该元素（计数排序）

代码实现：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        //需要使用哈希表
        unordered_map<int,int> counts;
        for(int i=0;i<n;i++){
            counts[nums[i]]++;
        }
        //遍历哈希表
        for(auto const&pair:counts){
            if(pair.second>n/2){
                 return pair.first;
            }
        }
        return -1;
    }
};

执行结果：

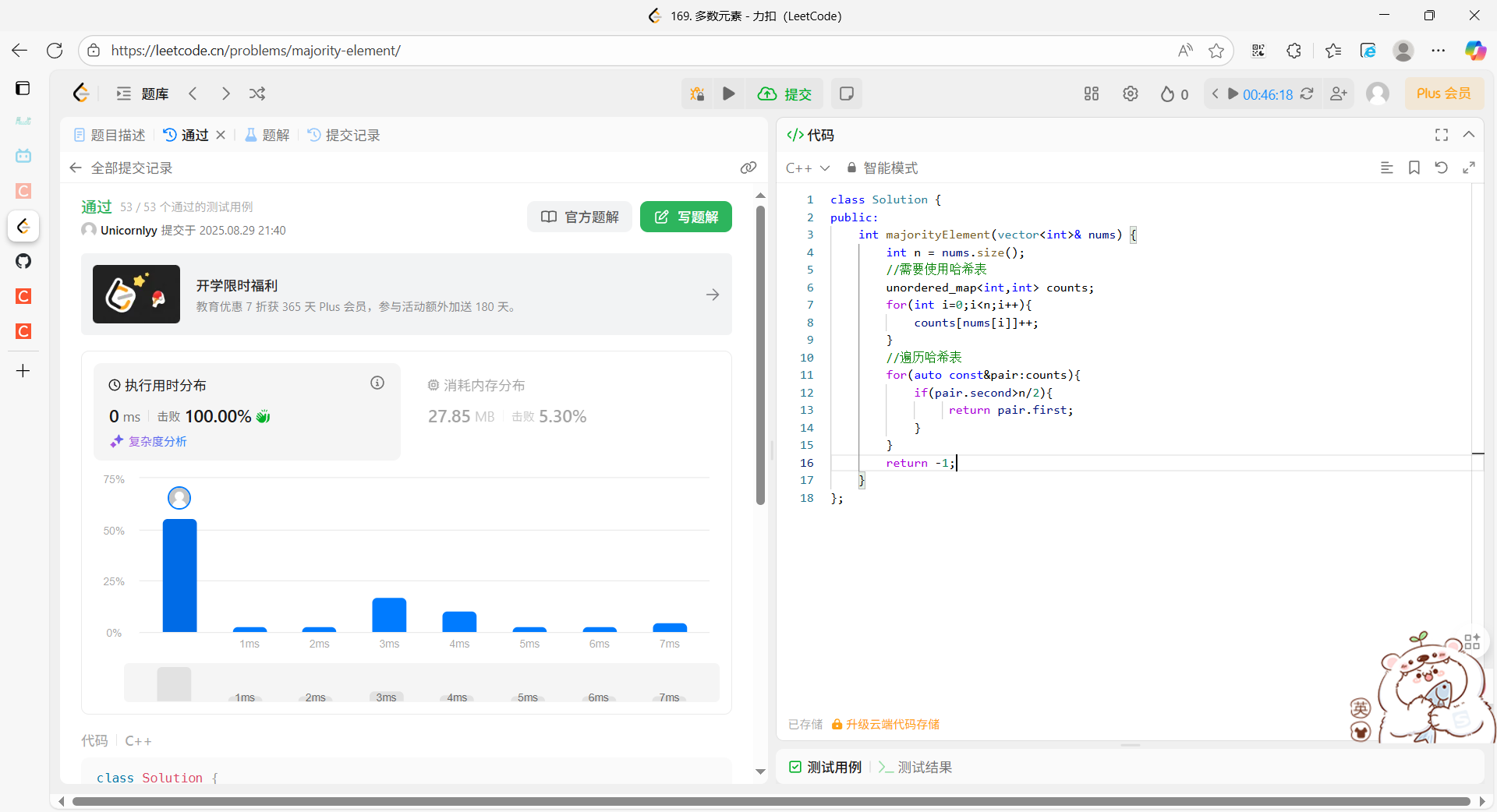
复杂度分析：

时间 O(n)

空间 O(n)

解法二 排序法

先排序nums，如果存在一个数出现的次数超过了数组长度的一半，那么将数组排序后，这个数必然会出现在数组中间的位置。

代码实现

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(),nums.end());
        return nums[n/2];
    }
};

执行结果

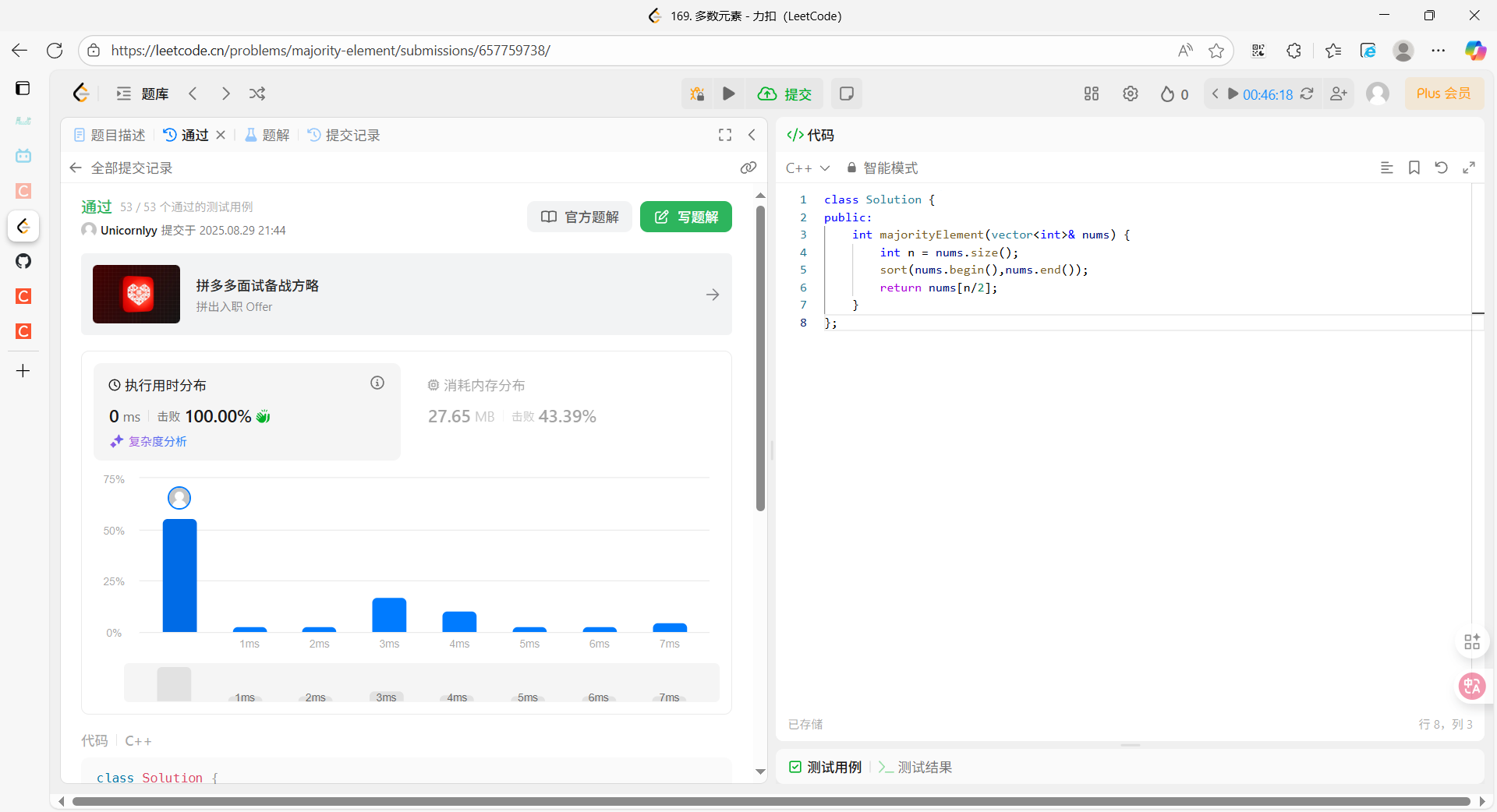
复杂度分析

时间:排序的时间复杂度为O(nlogn)

空间:O(1)

解法三：Boyer-Moore 投票算法 (最优解)

思路： 这是一个非常巧妙的算法。可以想象成不同阵营的人进行"消耗战"。

1. 我们维护一个 candidate (候选人) 和一个 count (计数器)。
2. 遍历数组，如果 count 为 0，就将当前元素设为 candidate。
3. 如果当前元素和 candidate 相同，count 加 1。
4. 如果当前元素和 candidate 不同，count 减 1 (相当于一组"同归于尽")。
5. 由于众数的数量超过了其他所有数字数量的总和，它最后一定会留下来成为 candidate。

实现代码

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n = nums.size();
        int candidate=0,count=0;
        for(int i=0;i<n;i++){
            if(count==0){
                candidate=nums[i];
            }
            if(candidate==nums[i]){
                count++;
            }else{
                count--;
            }
        }
        return candidate;
    }
};

执行结果

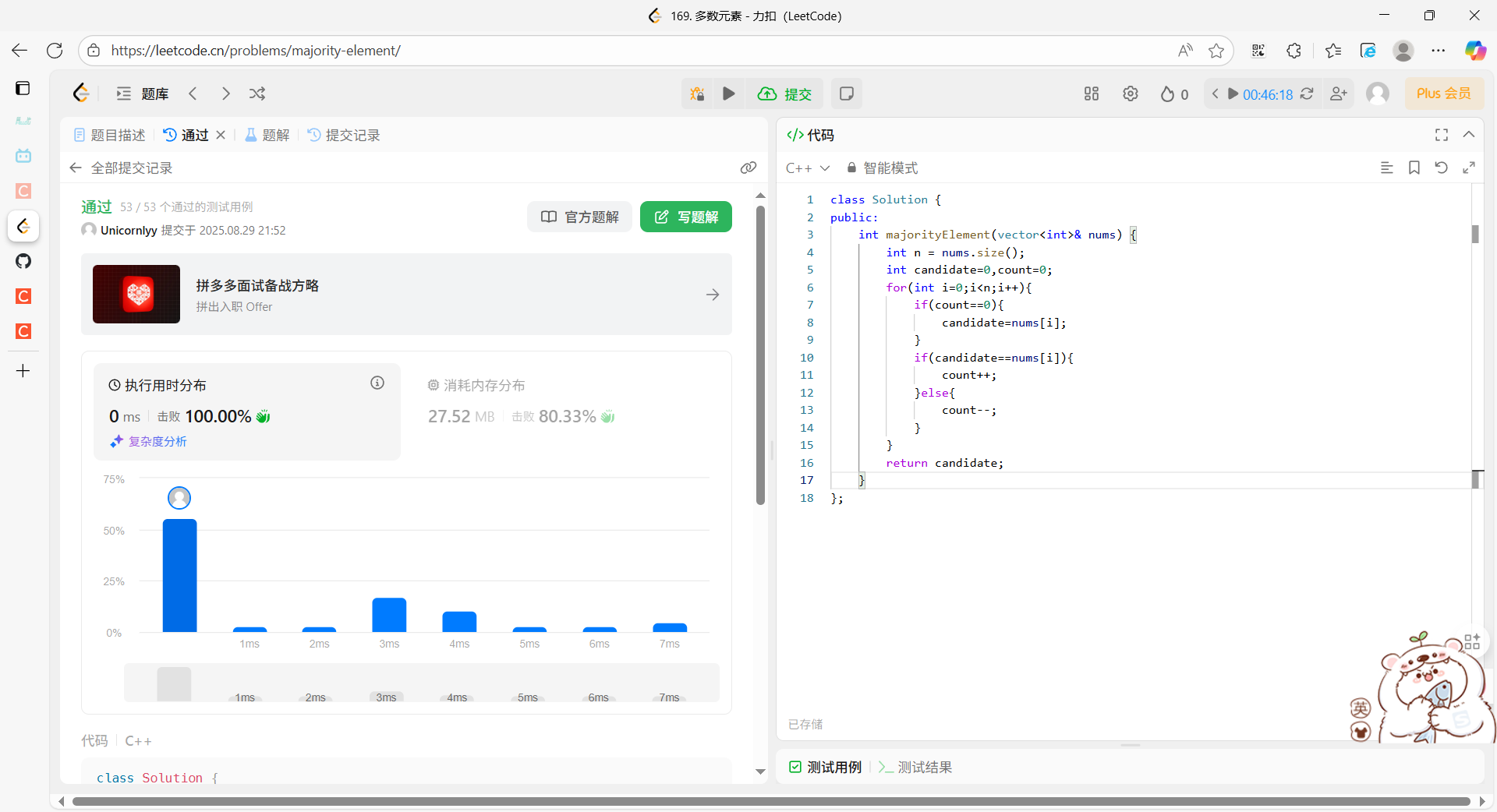
复杂度分析

时间O(n)

空间O(1)