贝叶斯向量自回归模型 (BVAR)

一、BVAR模型介绍

在金融时间序列分析中，向量自回归 (VAR) 模型作为一种基础且广泛应用的工具，能够捕捉多个时间序列变量之间的动态关系。传统 VAR 模型在参数估计时通常采用普通最小二乘法 (OLS)，但这种方法在样本量有限的情况下往往表现不佳，容易出现过拟合现象。贝叶斯向量自回归 (BVAR) 模型通过引入贝叶斯统计框架，能够有效利用先验信息对模型参数进行正则化，特别适合处理小样本数据问题。随着金融市场的复杂性增加和数据获取难度的提高，BVAR 模型在金融时间序列分析中的优势日益凸显。

二、BVAR 模型的理论背景

2.1 向量自回归 (VAR) 模型基础

向量自回归 (VAR) 模型是一种多变量时间序列分析方法，将系统中每一个内生变量作为所有内生变量滞后值的函数来构造模型，从而将单变量自回归模型推广到多变量系统。对于一个包含 n 个变量的 p 阶 VAR 模型 (VAR §)，其数学表达式为：

其中，

y_t是 n 维内生变量向量
A_1 ,...,A_p是 n×n 维系数矩阵
ϵ_t是 n 维随机误差向量

满足:

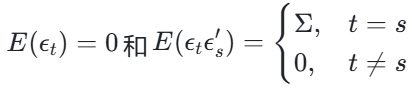
Σ是正定协方差矩阵

VAR 模型的优点在于结构简单、易于估计和解释，不需要严格的经济理论基础，可以直接从数据中学习变量间的动态关系。然而，传统 VAR 模型在变量较多或滞后阶数较大时，参数数量会急剧增加，导致 "维度灾难" 问题，尤其在样本量有限的情况下，参数估计的精度会显著下降。

2.2 贝叶斯统计框架下的 BVAR 模型

贝叶斯向量自回归 (BVAR) 模型是在传统 VAR 模型的基础上，引入贝叶斯统计框架发展而来的。与传统 VAR 模型相比，BVAR 模型的最大特点是将模型参数视为随机变量，并赋予其先验分布，然后根据观测数据更新先验分布得到后验分布，进而进行推断。
BVAR 模型的基本思想可以概括为：

参数的随机性理解： 将 VAR 模型中的系数矩阵A_1,...,A_p和协方差矩阵Σ视为随机变量，而不是固定但未知的常数。
先验信息的引入： 在观测数据之前，利用已有的知识或经验对模型参数的可能取值范围进行描述，形成先验分布。
后验分布的更新： 基于观测数据，利用贝叶斯定理将先验分布更新为后验分布，实现对模型参数的估计和推断。
预测分布的构建： 基于后验分布生成未来观测值的预测分布，从而量化预测结果的不确定性。

通过这种方式，BVAR 模型能够有效利用先验信息对模型参数进行正则化，特别适合处理小样本数据问题。

2.3 BVAR 模型在金融时间序列中的适用性

金融时间序列数据具有以下特点：波动性聚集、非正态性、非平稳性、结构突变等。BVAR 模型在处理这些特点方面具有独特优势：

波动性聚集处理： 通过引入随机波动率模型，可以有效捕捉金融时间序列的波动性聚集现象。
非正态性处理： 利用非共轭先验分布或非参数方法，可以灵活处理金融数据的非正态特性。
非平稳性处理： 通过引入趋势项、季节项或允许系数随时间变化，可以处理非平稳时间序列。
结构突变处理： 通过引入马尔可夫转换机制或时变参数，可以捕捉金融时间序列中的结构突变。

此外，金融数据通常具有高维度特性，BVAR 模型通过适当的先验设定，可以实现参数的有效收缩，避免过拟合，提高预测精度。特别是在金融市场发生极端事件时，传统模型往往失效，而 BVAR 模型由于其稳健的贝叶斯框架，能够更好地应对这些情况。

三、BVAR 模型的估计方法

3.1 先验分布的选择与设定

在 BVAR 模型中，先验分布的选择至关重要，它直接影响模型的估计结果和预测性能。常用的先验分布包括：

1.明尼苏达先验 (Minnesota Prior)：

这是 BVAR 模型中最常用的先验分布之一，最早由 Litterman (1986) 提出。明尼苏达先验的基本思想是对系数矩阵施加收缩，使得系数向零或某种特定模式收缩。具体来说，明尼苏达先验假设：

明尼苏达先验的数学表达式为：

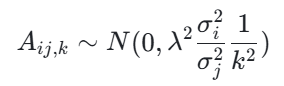
其中，A_ij,k表示第 i 个变量对第 j 个变量 k 阶滞后的系数，σ_i²和σ_j²分别表示第 i 个和第 j 个变量的方差，λ是收缩参数，控制收缩强度。

截距项服从正态分布。
自回归系数向 1 收缩（针对水平变量）或向 0 收缩（针对差分变量）。
交叉变量系数向 0 收缩。
高阶滞后系数比低阶滞后系数收缩更强。

2.正态 - Wishart 先验 (Normal-Wishart Prior)：

这是一种共轭先验，数学形式简单，计算方便。正态 - Wishart 先验假设：

正态 - Wishart 先验的数学表达式为：

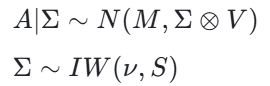
其中:

M是均值矩阵
V是正定矩阵
ν是自由度参数
S是正定矩阵
系数矩阵A=[A_1,...,A_p]服从正态分布
协方差矩阵Σ服从逆 Wishart 分布

3.稀疏先验 (Sparse Prior)：

针对高维 VAR 模型，为了实现系数的稀疏性，可以使用贝叶斯 Lasso、马蹄形先验 (Horseshoe Prior)、狄利克雷 - 拉普拉斯先验 (Dirichlet-Laplace Prior) 等。这些先验能够有效促进系数的稀疏性，特别适合变量较多的情况。

时变参数先验 (Time-Varying Parameter Prior)：

当金融时间序列存在结构变化时，可以使用时变参数先验，如随机游走先验、马尔可夫转换先验等。这些先验允许系数随时间变化，能够捕捉金融市场中的动态变化。

在实际应用中，先验分布的选择需要考虑以下因素：数据特性、模型复杂度、计算可行性、解释性要求等。对于金融时间序列数据，由于其高维度和复杂动态特性，通常需要选择能够实现系数收缩和捕捉时变特性的先验分布。

3.2 贝叶斯估计方法与算法

BVAR 模型的估计通常采用贝叶斯计算方法，主要包括：

1. 马尔可夫链蒙特卡洛方法 (MCMC)：

这是 BVAR 模型估计的主流方法，通过构建马尔可夫链，使其平稳分布为目标后验分布，从而实现从后验分布中抽样。常用的 MCMC 算法包括：

吉布斯抽样 (Gibbs Sampling)： 通过在每个步骤中从全条件分布中抽样，逐步构建整个后验分布。在 BVAR 模型中，吉布斯抽样特别有效，因为许多全条件分布具有已知的形式，可以直接抽样。
哈密尔顿蒙特卡洛方法 (HMC)： 利用哈密尔顿力学原理设计建议分布，能够更高效地探索后验分布空间，特别是对于高维问题。
无回跳抽样器 (NUTS)： 这是 HMC 的一种自适应版本，能够自动调整步长和路径长度，无需手动调参。

2.变分推断方法 (Variational Inference)：

这是一种近似贝叶斯推断方法，通过优化的方式寻找与目标后验分布最接近的近似分布。变分推断方法的计算速度通常比 MCMC 快，特别适合大数据和高维模型。

3.期望最大化算法 (EM Algorithm)：

这是一种迭代方法，用于估计包含隐变量的模型参数。在 BVAR 模型中，可以将缺失数据或潜在状态视为隐变量，应用 EM 算法进行估计。

在实际应用中，需要根据模型复杂度、数据规模、计算资源等因素选择合适的估计方法。对于复杂的 BVAR 模型，如包含随机波动率、时变参数或结构突变的模型，通常采用 MCMC 方法；而对于大规模数据或高维模型，可以考虑使用变分推断方法。

3.3 模型选择与评价标准

在 BVAR 模型应用中，模型选择是一个重要环节，主要包括：

滞后阶数选择： VAR 模型的滞后阶数 p 对模型性能有重要影响。贝叶斯因子 (Bayesian Factor) 是贝叶斯框架下比较不同滞后阶数模型的常用工具。
变量选择： 在高维 VAR 模型中，选择相关变量是一个关键问题。可以使用贝叶斯模型平均 (BMA)、变量选择先验等方法实现变量选择。
先验参数设定： 先验分布中的超参数需要合理设定，通常可以采用经验贝叶斯方法或超先验分布进行估计。

模型评价的标准主要包括：

预测性能指标： 如均方预测误差 (MSPE)、平均绝对误差 (MAE)、预测对数似然 (PLL) 等。
拟合优度指标： 如后验预测 p 值、贝叶斯信息准则 (BIC)、偏差信息准则 (DIC) 等。不确定性量化：如预测区间覆盖率、预测密度的校准度等。
不确定性量化： 如预测区间覆盖率、预测密度的校准度等。

在金融应用中，除了上述通用指标外，还需要考虑金融特定的评价标准，如 Sharpe 比率、VaR、CVaR 等。这些指标能够更好地反映模型在实际金融决策中的价值。

实际操作案例

一、库导入与数据准备

python 复制代码

import numpy as np
import pandas as pd
from scipy.stats import invwishart, multivariate_normal  # 贝叶斯推断所需的概率分布

除基础数据处理库外，引入了scipy中的概率分布（逆 Wishart 分布、多元正态分布），用于贝叶斯模型的参数抽样。

数据准备流程：

读取数据： 读取 Excel 文件 "降维结果.xlsx"，包含多变量时间序列数据（如特征变量和目标变量 "WTI 原油期货价格"）。
处理时间索引： 将日期列转换为datetime格式并设为索引，指定频率（如月度 "MS"），确保时间序列的完整性。
数据清洗： 转换为数值型数据并删除缺失值，保证模型输入的有效性。
划分数据集： 按 85%/15% 比例分为训练集（建模）和测试集（评估预测效果）。

python 复制代码

# ===== 数据准备部分 =====
# 读取Excel文件
df = pd.read_excel('降维结果.xlsx', sheet_name='Sheet1', engine='openpyxl')
print("Excel文件读取成功")

# 处理日期索引
df['date'] = pd.to_datetime(df['Unnamed: 0'], errors='coerce')
df.set_index('date', inplace=True)
df.drop(columns=['Unnamed: 0'], inplace=True)
df = df.asfreq('MS')  
print("已设置日期索引并指定频率")

# 确保数据是数值型
df = df.apply(pd.to_numeric, errors='coerce').dropna()
print(f"数据清洗后形状: {df.shape}")

# 划分训练集和测试集
train_size = int(0.85 * len(df))
train_data = df.iloc[:train_size]
test_data = df.iloc[train_size:]
print(f"训练集大小: {len(train_data)}, 测试集大小: {len(test_data)}")

二、核心：BayesianVAR 类的实现

这是代码的核心，封装了 BVAR 模型的所有功能，包括数据处理、先验设置、参数估计（Gibbs 抽样）、预测和显著性检验。

1. 初始化方法（init）

python 复制代码

def __init__(self, data, lags=1, nsim=1000, burnin=200, minnesota_prior=True, prior_kappa=0.2):
    self.data = data.values  # 转换为numpy数组
    self.lags = lags  # 滞后阶数
    self.nsim = nsim  # Gibbs抽样迭代次数
    self.burnin = burnin  # 预烧期（丢弃前burnin次抽样，保留稳定后的结果）
    self.minnesota_prior = minnesota_prior  # 是否使用Minnesota先验
    self.prior_kappa = prior_kappa  # Minnesota先验的调节参数
    self.T, self.n = self.data.shape  # T=样本量，n=变量数
    
    # 创建滞后矩阵（将时间序列转换为含滞后项的输入格式）
    self.Y, self.X = self._create_lag_matrix()
    
    # 初始化参数（beta为系数矩阵，Sigma为协方差矩阵）
    self.beta = np.zeros((self.n * lags + 1, self.n))
    self.Sigma = np.eye(self.n)
    
    # 存储Gibbs抽样结果
    self.beta_draws = np.zeros((nsim, self.n * lags + 1, self.n))
    self.Sigma_draws = np.zeros((nsim, self.n, self.n))

核心参数说明：

lags： 滞后阶数（用前几期数据预测当前值）
nsim： Gibbs 抽样次数（通过多次抽样近似后验分布）
burnin： 预烧期（前burnin次抽样不稳定，需丢弃，保留后续稳定结果）
minnesota_prior： 一种常用于 VAR 的贝叶斯先验（见下文详解）

2. 滞后矩阵创建（_create_lag_matrix）

python 复制代码

def _create_lag_matrix(self):
    Y = self.data[self.lags:, :]  # 因变量矩阵（从第lags行开始，即y_t）
    X = np.ones((self.T - self.lags, 1))  # 常数项列
    for lag in range(1, self.lags + 1):
        # 拼接滞后项（如y_{t-1}, y_{t-2}, ..., y_{t-lags}）
        X = np.hstack((X, self.data[self.lags - lag : -lag, :]))
    return Y, X

功能：将时间序列数据转换为适合回归的格式：

Y：每行是t时刻的所有变量值（待预测的目标）
X：每行包含常数项 + t-1到t-lags时刻的所有变量值（预测特征）

3. Minnesota 先验设置（_minnesota_prior）

这是 BVAR 的核心创新点之一，通过先验信息正则化参数估计（解决传统 VAR 在多变量时的过拟合问题）

python 复制代码

def _minnesota_prior(self):
    # 先验均值：假设每个变量对自身滞后1阶的系数为1（其他系数为0）
    beta_prior = np.zeros((self.n * self.lags + 1, self.n))
    for i in range(self.n):
        beta_prior[1 + i * self.lags, i] = 1.0  # 自身滞后1阶系数先验为1
    
    # 先验协方差矩阵（控制先验的"强度"）
    V_prior = np.zeros((self.n * self.lags + 1, self.n * self.lags + 1))
    V_prior[0, 0] = 10**2  # 常数项的先验方差（较大，表示弱先验）
    
    for i in range(self.n):
        for j in range(self.n):
            for lag in range(1, self.lags + 1):
                idx = 1 + j * self.lags + (lag - 1)  # 参数索引
                if i == j:  # 变量j对自身i的滞后项（赋予较强先验）
                    V_prior[idx, idx] = (self.prior_kappa / lag)**2
                else:  # 变量j对其他变量i的滞后项（赋予更弱先验）
                    V_prior[idx, idx] = (self.prior_kappa**2 / lag)**2
    return beta_prior, V_prior

Minnesota 先验的逻辑：

变量自身的滞后项对其影响更大（如油价的过去值对当前油价影响比其他变量大）
滞后阶数越高（如 t-2 比 t-1），影响越弱（方差随滞后阶数增大而减小）
prior_kappa控制先验强度：值越小，先验约束越强（参数更接近先验均值）

4. 模型拟合（fit）：Gibbs 抽样

贝叶斯推断中，后验分布通常难以直接计算，因此用Gibbs 抽样（一种 MCMC 方法）近似后验分布。

python 复制代码

def fit(self):
    Y, X = self.Y, self.X  # 因变量和自变量矩阵
    
    # 设置先验（Minnesota先验或无信息先验）
    if self.minnesota_prior:
        beta_prior, V_prior = self._minnesota_prior()
        V_prior_inv = np.linalg.inv(np.diag(np.diag(V_prior)))  # 先验精度矩阵
    else:
        beta_prior = np.zeros((self.n * self.lags + 1, self.n))
        V_prior_inv = np.zeros((self.n * self.lags + 1, self.n * self.lags + 1))  # 无信息先验
    
    # 协方差矩阵Sigma的共轭先验（逆Wishart分布）
    S_prior = np.eye(self.n)  # 先验尺度矩阵
    nu_prior = self.n + 2  # 先验自由度
    
    # Gibbs抽样：交替抽样beta和Sigma，直到收敛
    for i in range(self.nsim + self.burnin):
        # 1. 给定Sigma，抽样系数beta（后验为多元正态分布）
        V_post_inv = V_prior_inv + X.T @ X  # 后验精度 = 先验精度 + 数据信息
        V_post = np.linalg.inv(V_post_inv)  # 后验协方差
        beta_hat = V_post @ (V_prior_inv @ beta_prior + X.T @ Y)  # 后验均值
        
        # 对每个变量的系数进行抽样
        beta_draw = np.zeros_like(beta_hat)
        for j in range(self.n):
            cov_matrix = V_post * self.Sigma[j, j]  # 条件协方差
            beta_draw[:, j] = multivariate_normal.rvs(mean=beta_hat[:, j], cov=cov_matrix)
        
        # 2. 给定beta，抽样协方差矩阵Sigma（后验为逆Wishart分布）
        residuals = Y - X @ beta_draw  # 残差 = 实际值 - 预测值
        S_post = S_prior + residuals.T @ residuals  # 后验尺度矩阵
        nu_post = nu_prior + self.T - self.lags  # 后验自由度
        Sigma_draw = invwishart.rvs(df=nu_post, scale=S_post)  # 抽样Sigma
        
        # 更新参数
        self.beta = beta_draw
        self.Sigma = Sigma_draw
        
        # 存储稳定后的抽样结果（跳过预烧期）
        if i >= self.burnin:
            idx = i - self.burnin
            self.beta_draws[idx] = beta_draw
            self.Sigma_draws[idx] = Sigma_draw
    
    # 计算后验均值（用抽样结果的平均作为参数估计）
    self.beta_mean = np.mean(self.beta_draws, axis=0)
    self.Sigma_mean = np.mean(self.Sigma_draws, axis=0)

Gibbs 抽样核心逻辑：

贝叶斯推断中，参数beta（系数）和Sigma（协方差）的后验分布相互依赖，因此交替抽样：

固定Sigma，抽样beta（条件后验为多元正态分布）；
固定beta，抽样Sigma（条件后验为逆 Wishart 分布）；

重复多次后，抽样结果会收敛到真实后验分布，丢弃前burnin次不稳定结果，用剩余抽样的均值作为参数估计。

5. 预测（forecast）

python 复制代码

def forecast(self, steps=1):
    forecast = np.zeros((steps, self.n))  # 存储预测结果
    current_data = self.data[-self.lags:]  # 用训练集最后lags期数据作为预测起点
    
    for step in range(steps):
        # 构建预测用的滞后项矩阵（包含常数项+滞后数据）
        X_pred = np.ones((1, 1))
        for lag in range(self.lags):
            X_pred = np.hstack((X_pred, current_data[self.lags - lag - 1].reshape(1, -1)))
        
        # 用后验均值系数预测
        pred = X_pred @ self.beta_mean
        # 更新"当前数据"（滚动预测：用新预测值作为下一期的滞后项）
        current_data = np.vstack((current_data[1:], pred))
        forecast[step] = pred
    
    return forecast

功能：基于后验均值系数beta_mean，对未来steps期进行滚动预测（每一步的预测结果作为下一步的滞后项输入）

6. 参数显著性检验（parameter_significance）

python 复制代码

def parameter_significance(self, target_var, alpha=0.05):
    # 获取目标变量索引（如"WTI原油期货价格"）
    target_idx = list(df.columns).index(target_var)
    
    # 提取目标变量的系数后验抽样结果
    target_beta_draws = self.beta_draws[:, :, target_idx]
    
    # 分析每个参数的后验分布
    significance_results = []
    for param_idx in range(target_beta_draws.shape[1]):
        if param_idx == 0:  # 跳过常数项
            continue
            
        param_samples = target_beta_draws[:, param_idx]  # 该参数的所有抽样值
        # 计算95%置信区间（通过分位数）
        lower_bound = np.percentile(param_samples, (alpha/2)*100)
        upper_bound = np.percentile(param_samples, (1-alpha/2)*100)
        # 显著性判断：置信区间不包含0则显著
        significant = not (lower_bound <= 0 <= upper_bound)
        
        # 记录参数对应的变量名和滞后阶数
        var_idx = (param_idx - 1) // self.lags  # 对应哪个变量
        lag_order = (param_idx - 1) % self.lags + 1  # 对应第几阶滞后
        var_name = df.columns[var_idx]
        
        significance_results.append({
            'variable': var_name, 'lag': lag_order, 
            'posterior_mean': np.mean(param_samples),
            'lower_bound': lower_bound, 'upper_bound': upper_bound,
            'significant': significant
        })
    return significance_results

功能：分析其他变量的滞后项对目标变量（如 WTI 价格）的影响是否显著：

基于参数的后验抽样分布，计算 95% 置信区间
若置信区间不包含 0，则认为该参数显著非零（即该滞后项对目标变量有显著影响）

三、模型使用与评估

1. 模型初始化与拟合

python 复制代码

# 确定最大滞后阶数（同VAR，避免过拟合）
k = len(df.columns)
n = len(train_data)
max_lags = max(1, min(5, (n - k - 1) // (k + 1)))

# 创建BVAR模型实例
bvar_model = BayesianVAR(
    train_data, lags=max_lags, nsim=1000, burnin=200,
    minnesota_prior=True, prior_kappa=0.2
)

# 拟合模型（执行Gibbs抽样）
bvar_model.fit()

2. 参数显著性检验

针对目标变量 "WTI 原油期货价格"，输出各变量滞后项对其的显著影响：

python 复制代码

significance_results = bvar_model.parameter_significance(target_var='WTI原油期货价格')

结果包含变量名、滞后阶数、后验均值（影响强度）、95% 置信区间和显著性判断

3. 预测与评估

python 复制代码

# 预测测试集长度的结果
forecast_mean = bvar_model.forecast(steps=len(test_data))

# 评估指标（与VAR相同）
mae = np.mean(np.abs(actual - forecast))  # 平均绝对误差
rmse = np.sqrt(np.mean((actual - forecast)**2))  # 均方根误差
mape = np.mean(np.abs((actual - forecast)/actual)) * 100  # 平均绝对百分比误差

用后验均值系数生成预测，通过 MAE、RMSE、MAPE 评估预测精度（值越小越好）

完整代码

运行代码

python 复制代码

import numpy as np
import pandas as pd
import sys
from scipy.stats import invwishart, multivariate_normal

# ===== 数据准备部分 =====
# 读取Excel文件
df = pd.read_excel('降维结果.xlsx', sheet_name='Sheet1', engine='openpyxl')
print("Excel文件读取成功")

# 处理日期索引
df['date'] = pd.to_datetime(df['Unnamed: 0'], errors='coerce')
df.set_index('date', inplace=True)
df.drop(columns=['Unnamed: 0'], inplace=True)
df = df.asfreq('MS')  
print("已设置日期索引并指定频率")

# 确保数据是数值型
df = df.apply(pd.to_numeric, errors='coerce').dropna()
print(f"数据清洗后形状: {df.shape}")

# 划分训练集和测试集
train_size = int(0.85 * len(df))
train_data = df.iloc[:train_size]
test_data = df.iloc[train_size:]
print(f"训练集大小: {len(train_data)}, 测试集大小: {len(test_data)}")

# ===== BVAR模型实现 =====
class BayesianVAR:
    """贝叶斯向量自回归(BVAR)模型实现"""
    
    def __init__(self, data, lags=1, nsim=1000, burnin=200, minnesota_prior=True, prior_kappa=0.2):
        self.data = data.values
        self.lags = lags
        self.nsim = nsim
        self.burnin = burnin
        self.minnesota_prior = minnesota_prior
        self.prior_kappa = prior_kappa
        self.T, self.n = self.data.shape
        
        # 创建滞后矩阵
        self.Y, self.X = self._create_lag_matrix()
        
        # 初始化参数
        self.beta = np.zeros((self.n * lags + 1, self.n))
        self.Sigma = np.eye(self.n)
        
        # 存储Gibbs抽样结果
        self.beta_draws = np.zeros((nsim, self.n * lags + 1, self.n))
        self.Sigma_draws = np.zeros((nsim, self.n, self.n))
        
    def _create_lag_matrix(self):
        """创建滞后矩阵"""
        Y = self.data[self.lags:, :]
        X = np.ones((self.T - self.lags, 1))
        for lag in range(1, self.lags + 1):
            X = np.hstack((X, self.data[self.lags - lag : -lag, :]))
        return Y, X
    
    def _minnesota_prior(self):
        """设置Minnesota先验分布"""
        beta_prior = np.zeros((self.n * self.lags + 1, self.n))
        for i in range(self.n):
            beta_prior[1 + i * self.lags, i] = 1.0
            
        V_prior = np.zeros((self.n * self.lags + 1, self.n * self.lags + 1))
        V_prior[0, 0] = 10**2
        
        for i in range(self.n):
            for j in range(self.n):
                for lag in range(1, self.lags + 1):
                    idx = 1 + j * self.lags + (lag - 1)
                    if i == j:
                        V_prior[idx, idx] = (self.prior_kappa / lag)**2
                    else:
                        V_prior[idx, idx] = (self.prior_kappa * self.prior_kappa / lag)**2
        return beta_prior, V_prior
    
    def fit(self):
        """使用Gibbs抽样拟合BVAR模型"""
        Y, X = self.Y, self.X
        
        # 设置先验
        if self.minnesota_prior:
            beta_prior, V_prior_inv = self._minnesota_prior()
            V_prior_inv = np.linalg.inv(np.diag(np.diag(V_prior_inv)))
        else:
            beta_prior = np.zeros((self.n * self.lags + 1, self.n))
            V_prior_inv = np.zeros((self.n * self.lags + 1, self.n * self.lags + 1))
        
        # 共轭先验参数
        S_prior = np.eye(self.n)
        nu_prior = self.n + 2
        
        # Gibbs抽样
        for i in range(self.nsim + self.burnin):
            # 1. 抽取beta | Sigma
            V_post_inv = V_prior_inv + X.T @ X
            V_post = np.linalg.inv(V_post_inv)
            beta_hat = V_post @ (V_prior_inv @ beta_prior + X.T @ Y)
            
            beta_draw = np.zeros_like(beta_hat)
            for j in range(self.n):
                cov_matrix = V_post * self.Sigma[j, j]
                beta_draw[:, j] = multivariate_normal.rvs(
                    mean=beta_hat[:, j], 
                    cov=cov_matrix
                )
            
            # 2. 抽取Sigma | beta
            residuals = Y - X @ beta_draw
            S_post = S_prior + residuals.T @ residuals
            nu_post = nu_prior + self.T - self.lags
            Sigma_draw = invwishart.rvs(df=nu_post, scale=S_post)
            
            # 更新参数
            self.beta = beta_draw
            self.Sigma = Sigma_draw
            
            # 存储抽样结果
            if i >= self.burnin:
                idx = i - self.burnin
                self.beta_draws[idx] = beta_draw
                self.Sigma_draws[idx] = Sigma_draw
        
        # 计算后验均值
        self.beta_mean = np.mean(self.beta_draws, axis=0)
        self.Sigma_mean = np.mean(self.Sigma_draws, axis=0)
        
        print("BVAR模型拟合完成")
        print(f"Gibbs抽样: {self.nsim}次迭代, 预烧期: {self.burnin}次")
        
    def forecast(self, steps=1):
        """使用拟合的BVAR模型进行预测"""
        forecast = np.zeros((steps, self.n))
        current_data = self.data[-self.lags:]
        
        for step in range(steps):
            X_pred = np.ones((1, 1))
            for lag in range(self.lags):
                X_pred = np.hstack((X_pred, current_data[self.lags - lag - 1].reshape(1, -1)))
            pred = X_pred @ self.beta_mean
            current_data = np.vstack((current_data[1:], pred))
            forecast[step] = pred
        
        return forecast
    
    def parameter_significance(self, target_var, alpha=0.05):
        """
        计算参数的显著性检验
        target_var: 目标变量名称
        alpha: 显著性水平
        """
        # 获取目标变量在数据中的索引
        if target_var in df.columns:
            target_idx = list(df.columns).index(target_var)
        else:
            print(f"错误: 目标变量 '{target_var}' 不存在")
            return
        
        # 提取目标变量的参数后验分布
        target_beta_draws = self.beta_draws[:, :, target_idx]
        
        # 计算每个参数的置信区间
        n_params = target_beta_draws.shape[1]
        significance_results = []
        
        for param_idx in range(n_params):
            # 跳过常数项
            if param_idx == 0:
                continue
                
            param_samples = target_beta_draws[:, param_idx]
            
            # 计算置信区间
            lower_bound = np.percentile(param_samples, (alpha/2)*100)
            upper_bound = np.percentile(param_samples, (1-alpha/2)*100)
            
            # 判断是否显著 (置信区间是否包含0)
            significant = not (lower_bound <= 0 <= upper_bound)
            
            # 计算后验均值
            posterior_mean = np.mean(param_samples)
            
            # 获取参数对应的变量名和滞后阶数
            var_idx = (param_idx - 1) // self.lags
            lag_order = (param_idx - 1) % self.lags + 1
            var_name = df.columns[var_idx]
            
            significance_results.append({
                'variable': var_name,
                'lag': lag_order,
                'posterior_mean': posterior_mean,
                'lower_bound': lower_bound,
                'upper_bound': upper_bound,
                'significant': significant
            })
        
        return significance_results

# ===== 使用BVAR模型 =====
# 确定滞后阶数
k = len(df.columns)
n = len(train_data)
max_lags = max(1, min(5, (n - k - 1) // (k + 1)))
print(f"计算的最大安全滞后阶数: {max_lags}")

# 创建BVAR模型
bvar_model = BayesianVAR(
    train_data,
    lags=max_lags,
    nsim=1000,
    burnin=200,
    minnesota_prior=True,
    prior_kappa=0.2
)

# 拟合模型
bvar_model.fit()

# ===== 参数显著性检验 =====
# 明确目标变量名称
target_var = 'WTI原油期货价格'  # 根据你的数据调整这个变量名
print(f"\n===== {target_var}的参数显著性检验 =====")

# 进行参数显著性检验
significance_results = bvar_model.parameter_significance(target_var, alpha=0.05)

# 打印显著性结果
if significance_results:
    print("\n变量\t\t滞后阶数\t后验均值\t95%置信区间\t\t显著性(α=0.05)")
    print("-" * 80)
    for result in significance_results:
        var_name = result['variable']
        lag = result['lag']
        mean_val = result['posterior_mean']
        lower = result['lower_bound']
        upper = result['upper_bound']
        sig = "显著" if result['significant'] else "不显著"
        
        print(f"{var_name}\t{lag}\t\t{mean_val:.4f}\t[{lower:.4f}, {upper:.4f}]\t{sig}")
else:
    print("未获得显著性检验结果")

# ===== 预测部分 =====
forecast_steps = len(test_data)
forecast_mean = bvar_model.forecast(steps=forecast_steps)

# 构建预测结果DataFrame
forecast_df = pd.DataFrame(
    forecast_mean, 
    index=test_data.index,
    columns=[f"{col}_forecast" for col in df.columns]
)

# 合并实际值和预测值
results_df = pd.concat([test_data, forecast_df], axis=1)

# ===== 模型评估 =====
print("\n模型评估:")
for col in df.columns:
    forecast_col = f"{col}_forecast"
    if forecast_col in results_df.columns:
        actual = results_df[col].dropna()
        forecast = results_df[forecast_col].dropna()
        
        if len(actual) > 0 and len(forecast) > 0:
            min_len = min(len(actual), len(forecast))
            actual = actual.iloc[:min_len]
            forecast = forecast.iloc[:min_len]
            
            mae = np.mean(np.abs(actual - forecast))
            rmse = np.sqrt(np.mean((actual - forecast)**2))
            mape = np.mean(np.abs((actual - forecast)/actual)) * 100 if (actual != 0).any() else np.nan
            
            print(f"\n{col} 预测性能:")
            print(f"平均绝对误差 (MAE): {mae:.4f}")
            print(f"均方根误差 (RMSE): {rmse:.4f}")
            if not np.isnan(mape):
                print(f"平均绝对百分比误差 (MAPE): {mape:.2f}%")
        else:
            print(f"\n{col}: 无法计算评估指标，数据不足")
    else:
        print(f"\n{col}: 无预测数据可用于评估")

运行结果

bash 复制代码

Excel文件读取成功
已设置日期索引并指定频率
数据清洗后形状: (68, 5)
训练集大小: 57, 测试集大小: 11
计算的最大安全滞后阶数: 5
BVAR模型拟合完成
Gibbs抽样: 1000次迭代, 预烧期: 200次

===== WTI原油期货价格的参数显著性检验 =====

变量		滞后阶数	后验均值	95%置信区间		显著性(α=0.05)
--------------------------------------------------------------------------------
WTI原油期货价格	1		0.9957	[0.9676, 1.0238]	显著
WTI原油期货价格	2		0.0012	[-0.0138, 0.0154]	不显著
WTI原油期货价格	3		-0.0000	[-0.0092, 0.0088]	不显著
WTI原油期货价格	4		-0.0002	[-0.0072, 0.0076]	不显著
WTI原油期货价格	5		-0.0001	[-0.0056, 0.0052]	不显著
农业品期货综合因子	1		-0.0048	[-0.0312, 0.0239]	不显著
农业品期货综合因子	2		0.0005	[-0.0140, 0.0141]	不显著
农业品期货综合因子	3		0.0002	[-0.0095, 0.0093]	不显著
农业品期货综合因子	4		-0.0001	[-0.0072, 0.0067]	不显著
农业品期货综合因子	5		-0.0002	[-0.0059, 0.0057]	不显著
金属品期货综合因子	1		-0.0033	[-0.0308, 0.0237]	不显著
金属品期货综合因子	2		-0.0008	[-0.0144, 0.0136]	不显著
金属品期货综合因子	3		-0.0004	[-0.0097, 0.0085]	不显著
金属品期货综合因子	4		-0.0003	[-0.0071, 0.0067]	不显著
金属品期货综合因子	5		-0.0002	[-0.0058, 0.0056]	不显著
能源期货综合因子	1		-0.0029	[-0.0291, 0.0256]	不显著
能源期货综合因子	2		-0.0012	[-0.0155, 0.0127]	不显著
能源期货综合因子	3		-0.0001	[-0.0090, 0.0093]	不显著
能源期货综合因子	4		-0.0003	[-0.0072, 0.0068]	不显著
能源期货综合因子	5		-0.0001	[-0.0056, 0.0052]	不显著
宏观金融指数	1		-0.0367	[-0.1310, 0.0510]	不显著
宏观金融指数	2		-0.0053	[-0.0586, 0.0519]	不显著
宏观金融指数	3		0.0029	[-0.0418, 0.0475]	不显著
宏观金融指数	4		-0.0009	[-0.0352, 0.0334]	不显著
宏观金融指数	5		-0.0054	[-0.0331, 0.0205]	不显著

模型评估:

WTI原油期货价格 预测性能:
平均绝对误差 (MAE): 0.2710
均方根误差 (RMSE): 0.3694
平均绝对百分比误差 (MAPE): 167.50%

农业品期货综合因子 预测性能:
平均绝对误差 (MAE): 1.4810
均方根误差 (RMSE): 1.5401
平均绝对百分比误差 (MAPE): 105.91%

金属品期货综合因子 预测性能:
平均绝对误差 (MAE): 2.6738
均方根误差 (RMSE): 2.8184
平均绝对百分比误差 (MAPE): 100.43%

能源期货综合因子 预测性能:
平均绝对误差 (MAE): 0.4936
均方根误差 (RMSE): 0.6658
平均绝对百分比误差 (MAPE): 191.46%

宏观金融指数 预测性能:
平均绝对误差 (MAE): 1.4537
均方根误差 (RMSE): 1.4977
平均绝对百分比误差 (MAPE): 94.21%