数据结构（C语言篇）：（十二）实现顺序结构二叉树——堆

目录

前言

一、堆的概念与结构

二、堆的实现

[2.1 实现堆的结构](#2.1 实现堆的结构)

[2.2 头文件的准备](#2.2 头文件的准备)

[2.3 函数的实现](#2.3 函数的实现)

[2.3.1 HPInit( )函数（初始化）](#2.3.1 HPInit( )函数（初始化）)

（1）实现逻辑

（2）底层原理

（3）应用示例

（4）执行流程

[2.3.2 HPDestrroy( ) 函数（销毁）](#2.3.2 HPDestrroy( ) 函数（销毁）)

（1）实现逻辑

（2）底层原理

（3）应用示例

（4）执行流程

[2.3.3 AdjustUp( )函数（向上调整算法）](#2.3.3 AdjustUp( )函数（向上调整算法）)

（1）实现逻辑

（2）底层原理

（3）执行流程

（4）建堆时间复杂度

[2.3.4 HPPush( )函数（入堆）](#2.3.4 HPPush( )函数（入堆）)

（1）实现逻辑

（2）底层原理

（3）应用示例

（4）执行流程

[2.3.5 AdjustDown( )函数（向下调整算法）](#2.3.5 AdjustDown( )函数（向下调整算法）)

（1）实现逻辑

（2）底层原理

（3）执行流程

（4）建堆时间复杂度

[2.3.6 HPPop( )函数（出堆）](#2.3.6 HPPop( )函数（出堆）)

（1）实现逻辑

（2）底层原理

（3）应用示例

（4）执行流程

总结

---

前言

堆结构是计算机科学中一种高效且广泛应用的数据结构，尤其适合需要动态优先级管理的场景，如任务调度、图算法（Dijkstra、Prim）以及堆排序等。其核心特性在于能以对数时间复杂度维护元素的优先级关系，同时保证根节点始终为最大值（大顶堆）或最小值（小顶堆）。

C语言因其贴近硬件的特性，成为实现底层数据结构的理想选择。通过手动管理内存和指针操作，开发者可以精准控制堆的构建、调整与销毁过程，深入理解其核心逻辑。本文将系统性地探讨堆的理论基础，并基于C语言从零实现动态扩容、插入删除、堆化等关键操作，结合代码示例分析性能优化策略，为后续算法实践提供可靠的基础组件。下面就让我们正式开始吧！

---

一、堆的概念与结构

在上一篇博客中，我为大家介绍了二叉树的一些相关基本概念，其中就包含了顺序结构二叉树这一概念。顺序结构二叉树使用数组存储节点，通过下标关系表示父子节点位置。根节点通常存放在数组索引1处，左子节点为2i，右子节点为2i+1（i为父节点下标）。这种结构适合完全二叉树，非完全二叉树会存在空间浪费。而堆就是一种顺序结构的二叉树。

如果有一个关键码的集合，把它的所有元素按照完全二叉树的顺序存储方式存储，在一个一维数组中，同时满足：

i = 0 , 1 , 2 , ...... ，则称其为小堆（或称为大堆）。将根节点最大的堆称为最大堆或者大根堆，根结点最小的堆称为最小堆或者小根堆。

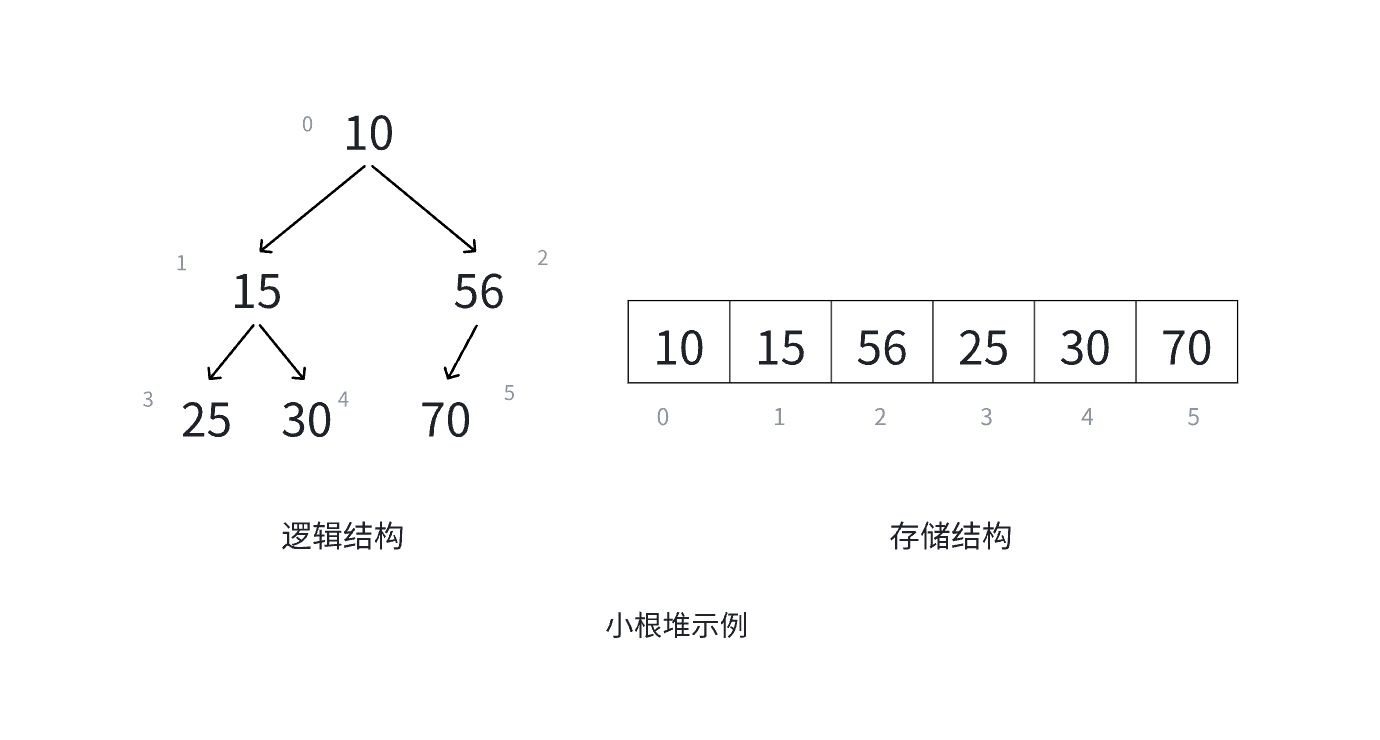
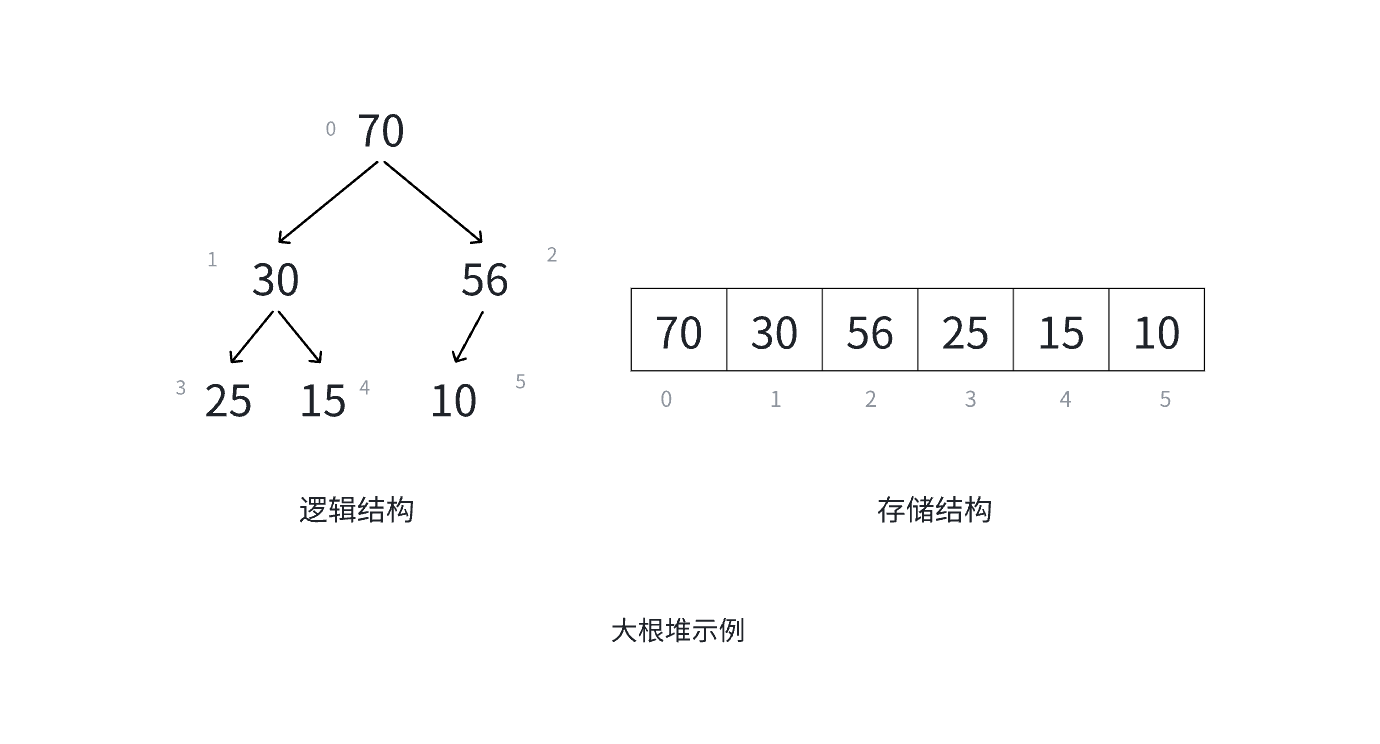
堆具有如下的性质：

• 堆中的某个结点的值总是不大于或者不小于其父结点的值；
• 堆总是一棵完全二叉树。

二、堆的实现

2.1 实现堆的结构

我们采用数组来实现堆的结构，为什么呢？

这是因为数组在内存中是连续存储的，通过索引可以快速访问任意元素，时间复杂度为 O(1)。堆的逻辑结构是一棵完全二叉树，而完全二叉树的特性恰好可以通过数组的连续内存布局高效映射：对于索引为 i 的节点，其左子节点索引为 2i+1，右子节点为 2i+2，父节点为 (i-1)/2（向下取整）。这种隐式的父子关系可以有效避免指针存储开销，同时利用 CPU 缓存局部性提升访问效率。

因此我们对堆的结构定义如下：

typedef int HPDataType;
typedef struct Heap
{
    HPDataType* a;
    int size;
    int capacity;
}HP;

2.2 头文件的准备

我们将需要用到的函数声明在头文件 Heap.h 中，后文将逐个展开分析。如下所示：

//定义堆结构
typedef int HPDataType;
typedef struct Heap {
	HPDataType* arr;
	int size;    //有效数据个数
	int capaicty;//空间大小
}HP;

void HPInit(HP* php);
void HPDesTroy(HP* php);

void HPPrint(HP* php);
void Swap(int* x, int* y);
//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n);
//向上调整算法
void AdjustUp(HPDataType* arr, int child);

void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);
HPDataType HPTop(HP* php);

bool HPEmpty(HP* php);

2.3 函数的实现

2.3.1 HPInit( )函数（初始化）

（1）实现逻辑

函数首先需要通过assert(php)来验证堆指针的有效性，防止对空指针操作；接着需要将堆的底层数组指针arr初始化为NULL（堆尚未分配内存空间）；将size（当前堆中的元素数量）初始哈鱼为0；最后将capacity（堆的容量，即底层数组可以容纳的最大元素数）初始化为0。

完整代码如下：

void HPInit(HP* php)
{
	assert(php);

	php->arr = NULL;
	php->size = php->capaicty = 0;
}

（2）底层原理

初始化的核心是建立 "空堆" 的基准状态：

• arr = NULL：未分配数组内存，符合空堆的物理状态
• size = 0：明确堆中没有任何元素（堆的逻辑大小）
• capacity = 0：明确当前可容纳元素的上限为 0

（3）应用示例

#include <stdio.h>
#include <assert.h>

int main() {
    HP heap;
    // 1. 初始化堆（必须先执行）
    HPInit(&heap);
    
    // 2. 后续堆操作（如插入元素、删除堆顶等）
    // HPInsert(&heap, 10);  // 插入元素
    // HPRemoveTop(&heap);   // 删除堆顶元素
    // ...
    
    // 3. 销毁堆（对应初始化的收尾操作）
    // HPDestroy(&heap);
    
    return 0;
}

（4）执行流程

1. 调用者创建HP类型变量（如栈上的heap），并传入其地址&heap。
2. 函数首先检查php是否为NULL：
   • 若为NULL，assert触发错误（调试阶段），程序终止
   • 若不为NULL，继续执行初始化
3. 将堆的数组指针arr置为NULL（未分配内存）。
4. 将size和capacity同时置为 0，明确空堆状态。
5. 函数返回，堆处于可操作的初始状态，可进行后续的插入等操作。

2.3.2 HPDestrroy( ) 函数（销毁）

（1）实现逻辑

1. 先通过assert( )函数来验证堆指针的有效性（确保操作的是一个合法的堆结构）；

2. 如果堆的底层数组arr不为NULL（即曾经分配过内存），则通过free释放数组占用的动态内

存；

3. 将arr指针置为NULL（能够避免野指针的问题）；

4. 重置size和capacity为0，并把堆标记为"空状态"。

完整代码如下：

void HPDesTroy(HP* php)
{
	assert(php);
	if (php->arr)
		free(php->arr);
	php->arr = NULL;
	php->size = php->capaicty = 0;
}

（2）底层原理

堆的底层实现是依赖动态数组的（arr指向的内存通过malloc/realloc分配），这类内存是不会自动释放的，必须显式调用free来进行释放。

销毁函数实现的核心逻辑是"资源释放"，其具体逻辑如下：

1. 条件判断if (php->arr)： 避免对NULL指针调用free。
2. **free(php->arr)：**释放动态数组占用的内存，归还给操作系统。
3. **指针置空与数值重置：**防止后续误操作访问已释放的内存（野指针），同时将堆状态重置为初始空状态。

（3）应用示例

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

// 堆结构体定义
typedef struct {
    int* arr;       // 存储堆元素的数组
    int size;       // 当前元素个数
    int capacity;   // 堆的容量
} HP;

// 假设存在堆插入函数
void HPInsert(HP* php, int val) {
    // 实现逻辑：检查容量、扩容、插入元素、向上调整等
}

int main() {
    HP heap;
    // 1. 初始化堆
    HPInit(&heap);
    
    // 2. 使用堆：插入元素
    HPInsert(&heap, 10);
    HPInsert(&heap, 20);
    HPInsert(&heap, 5);
    
    // 3. 堆使用完毕，销毁堆（释放资源）
    HPDesTroy(&heap);  // 此时heap.arr为NULL，size和capacity为0
    
    return 0;
}

（4）执行流程

1. 调用者传入堆结构体的指针（如&heap）。
2. 函数首先通过assert(php)检查指针有效性：
   • 若php为NULL，触发断言错误（调试阶段），程序终止；
   • 若php有效，继续执行销毁逻辑。
3. 检查堆的底层数组arr是否为NULL：若arr不为NULL（即存在动态分配的内存），调用free(php->arr)释放内存。
4. 将arr指针置为NULL（避免后续访问已释放的内存）。
5. 将size和capacity重置为 0，标记堆为 "空状态"。
6. 函数返回，堆占用的动态内存已释放，结构体本身可安全销毁（如栈上的heap变量会随作用域结束自动释放）。

2.3.3 AdjustUp( )函数（向上调整算法）

（1）实现逻辑

向上调整算法的作用是，当堆中插入新元素后，通过向上调整使堆重新满足堆的性质（考虑大堆或小堆）。

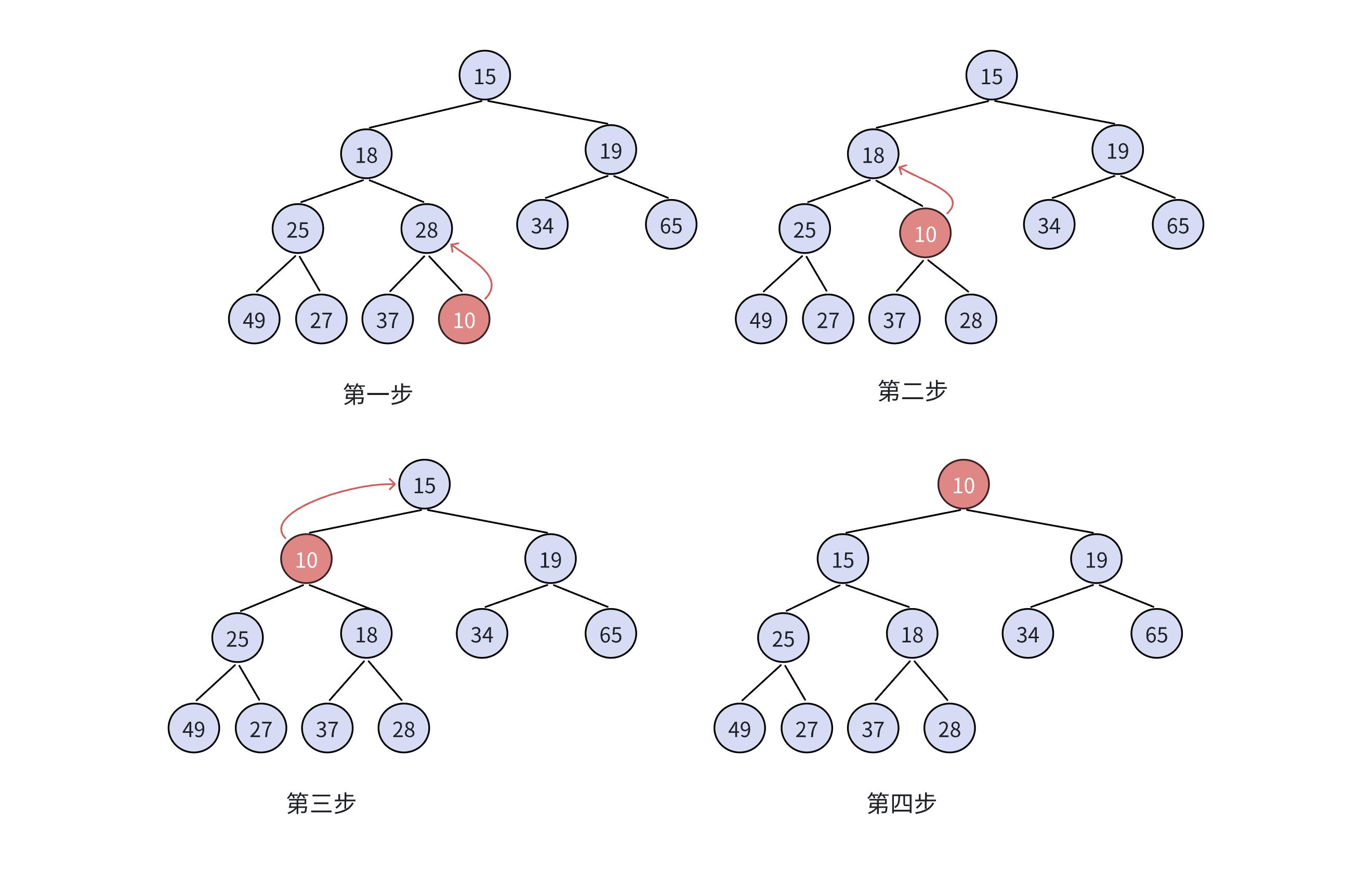
它的核心操作逻辑如下：

• 接收两个参数： 堆的底层数组arr和新插入元素的索引child。
• 计算child对应的父节点索引 parent = (child - 1) / 2（完全二叉树的父子节点关系）。
• **通过循环向上比较：**若子节点与父节点不满足堆的性质，则交换两者位置。
• 更新child为原父节点索引，继续向上比较，直到根节点或满足堆性质为止。

完整代码如下：

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//向上调整算法
void AdjustUp(HPDataType* arr,int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//建大堆：>
		//建小堆: <
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}

Tips： 这里我们使用arr[child] < arr[parent]的判断条件，即这是针对小堆 的调整（若改为>则适用于大堆）。

（2）底层原理

向上调整的底层逻辑是基于完全二叉树的父子节点关系的：

• 对于索引为child的节点，其父节点索引恒为(child - 1) // 2（整数除法）。
• 当新元素插入到堆的末尾（即数组尾部）时，可能破坏堆的性质，需要从该位置向上 "冒泡" 调整。
• 调整过程是一个迭代比较 - 交换的过程，直到新元素找到合适的位置（满足父节点与子节点的大小关系）。

这种调整算法的时间复杂度为（n为堆的大小），因为完全二叉树的高度为log n级别。

（3）执行流程

假设在小堆中插入新元素后，child为新元素的索引，那么函数的执行流程如下：

1. 计算父节点索引： parent = (child - 1) / 2
2. 进入循环 （条件：child > 0，即未到达根节点）：

比较arr[child]与arr[parent]：

• 若arr[child] < arr[parent]（小堆不满足）：交换两者的值，更新child = parent，重新计算parent；
• 若满足arr[child] >= arr[parent]：说明堆的性质已恢复，跳出循环。

3.循环结束，堆的性质已修复。

（4）建堆时间复杂度

因为堆是完全⼆叉树，⽽满⼆叉树也是完全⼆叉树，在这里我们为了简化，使用满⼆叉树来证明(时间复杂度本来看的就是近似值，多⼏个结点是不影响最终结果的)。

分析如下：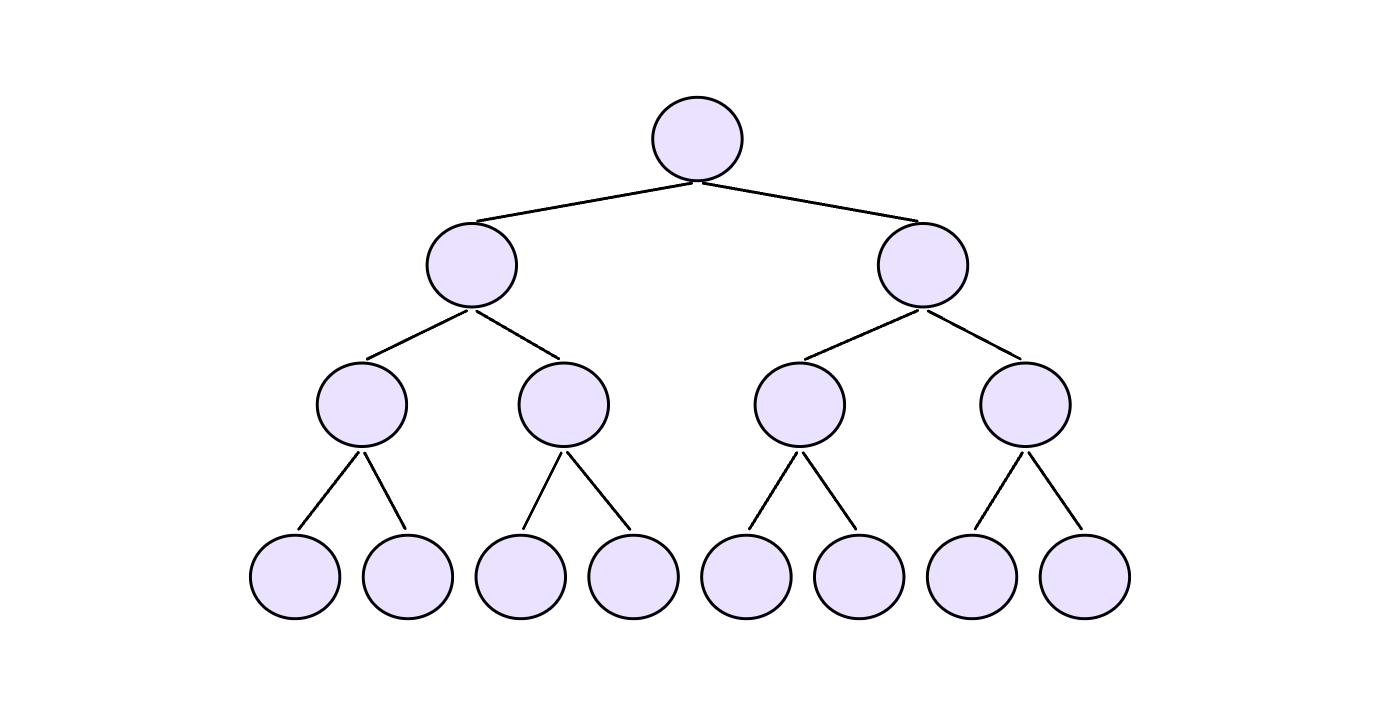

第1层， 20 个结点，需要向上移动0层；

第2层， 21 个结点，需要向上移动1层；

第3层， 22 个结点，需要向上移动2层；

第4层， 23 个结点，需要向上移动3层；

......

第h层， 2h-1 个结点，需要向上移动h-1层。

则需要移动结点总的移动步数为：每层结点个数 * 向上调整次数 （第⼀层调整次数为0）

①

②

②-①，进行错位相减，最终可以得到：

根据二叉树的性质可以知道：和，带入上式可得：

由此可得：向上调整算法建堆时间复杂度为： 。

2.3.4 HPPush( )函数（入堆）

（1）实现逻辑

1. 首先通过assert(php)验证堆指针的有效性；
2. 检查堆的当前容量：若元素数量size等于容量capacity，则进行扩容；
3. 若初始容量为 0 则扩容至 4，否则翻倍扩容（2 倍原容量）；
4. 扩容成功后，将新元素x插入到堆的末尾（数组的size位置）；
5. 调用AdjustUp函数对新插入的元素进行向上调整，确保堆的性质不被破坏；
6. 最后将堆的元素数量size加 1。

整个入堆操作的逻辑遵循的是"先确保空间充足→插入元素→维护堆性质" 的流程。

完整代码如下：

void HPPush(HP* php, HPDataType x)
{
	assert(php);
	//空间不够要增容
	if (php->size == php->capaicty)
	{
		//增容
		int newCapacity = php->capaicty == 0 ? 4 : 2 * php->capaicty;
		HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		php->arr = tmp;
		php->capaicty = newCapacity;
	}
	//空间足够
	php->arr[php->size] = x;
	//向上调整
	AdjustUp(php->arr, php->size);
	++php->size;
}

（2）底层原理

1. 动态扩容机制： 堆的底层数组是动态分配的，当元素数量达到容量上限时，必须通过realloc重新分配更大的内存块。采用 "翻倍扩容" 策略（初始为 4）的原因是：

减少频繁扩容的开销（时间复杂度 amortized O (1)）；

符合完全二叉树的生长特性，为后续元素插入预留足够空间。

2. 堆的尾部插入： 堆作为完全二叉树，新元素总是插入到数组末尾（对应二叉树的最后一个叶子节点位置），这是保持完全二叉树结构的必要条件。

3. 向上调整的必要性： 新元素插入后可能破坏堆的性质（如小堆中儿子节点小于父节点），AdjustUp通过逐层向上比较交换，使堆重新满足父节点与子节点的大小关系。

（3）应用示例

// 假设HP结构体和相关函数定义如下
typedef int HPDataType;
typedef struct {
    HPDataType* arr;  // 堆的底层数组
    int size;         // 当前元素个数
    int capacity;     // 容量
} HP;

// 假设已实现HPInit、AdjustUp、HPDesTroy等函数

int main() {
    HP heap;
    HPInit(&heap);  // 初始化空堆
    
    // 向堆中插入元素
    HPPush(&heap, 5);
    HPPush(&heap, 3);  // 插入后会触发AdjustUp
    HPPush(&heap, 7);
    HPPush(&heap, 1);  // 插入后会触发AdjustUp
    HPPush(&heap, 9);
    
    // 若为小堆，此时堆顶元素应为最小值1
    printf("堆顶元素: %d\n", heap.arr[0]);  // 输出1
    
    HPDesTroy(&heap);
    return 0;
}

（4）执行流程

• 调用HPPush(&heap, x)，传入堆指针和待插入元素x。
• 验证php不为NULL（assert检查）。
• 容量检查与扩容：

若**size == capacity**（空间不足）：

计算新容量（初始为 4，否则翻倍）；

调用realloc重新分配内存，若失败则报错退出；

更新arr指针和capacity为新值。

若空间充足，直接进入下一步。

• 插入元素：将x存入arr[size]（堆的末尾位置）。
• 维护堆性质：调用AdjustUp(arr, size)，从新元素位置向上调整。
• 更新堆大小：size加 1，函数返回。

2.3.5 AdjustDown( )函数（向下调整算法）

（1）实现逻辑

当堆的根节点或某父节点被修改后，我们需要通过向下调整使堆重新满足堆的性质（大堆或小堆）。向下调整算法有⼀个前提：左右子树必须是⼀个堆，才能调整。

该算法的核心操作如下：

1. 接收三个参数： 堆的底层数组arr、需要调整的父节点索引parent、堆的元素总数n（用于判断边界）

2. 计算parent对应的左孩子节点索引 child = parent * 2 + 1（完全二叉树的父子节点关系）

3. 进入循环调整：

首先在左右孩子中选择 "更符合堆性质" 的孩子（代码中是小堆逻辑，选择值更小的孩子）；

比较选中的孩子与父节点：若不满足堆的性质，则交换两者位置；

更新parent为原孩子节点索引，重新计算child，继续向下比较；

直到孩子节点超出堆的范围（child >= n）或满足堆性质为止。

4. 代码中使用**arr[child] > arr[child + 1]和arr[child] < arr[parent]** 的判断条件，表明这是针对小堆 的调整（若修改比较符号可适配大堆）。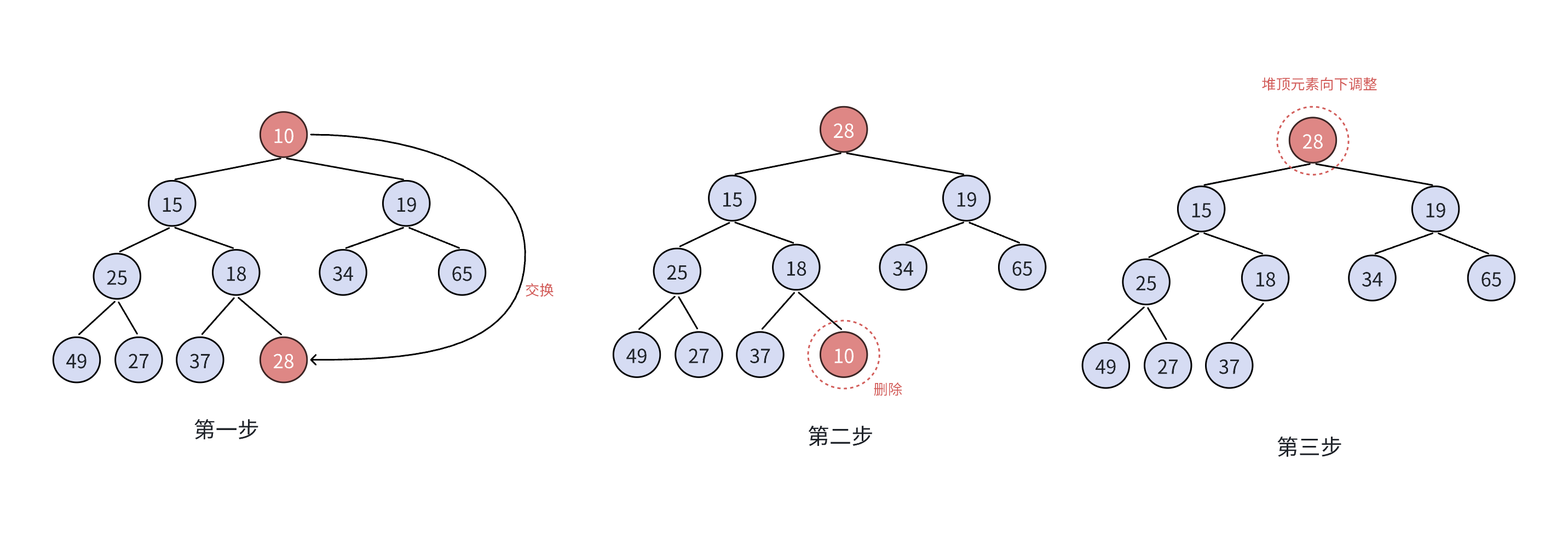

完整代码如下：

//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建大堆：<
		//建小堆: >
		if (child + 1 < n && arr[child] > arr[child + 1])
		{
			child++;
		}
		//孩子和父亲比较
		//建大堆：>
		//建小堆:<
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

（2）底层原理

当父节点可能不满足堆的性质时（如父节点值大于子节点值的小堆），需要将父节点与更符合条件的子节点交换，并继续向下检查，直到找到合适的位置。向下调整算法是**"自顶向下"**的调整，适用于删除堆顶或建堆。

时间复杂度：（n为堆的大小），因为调整深度最多为堆的高度。

（3）执行流程

假设在小堆中对根节点（parent=0）进行调整，堆的元素总数为n，执行流程如下：

1. 计算左孩子索引： child = parent * 2 + 1（初始为 1）。

2. 进入循环 （条件：child < n，即孩子节点在堆范围内）：

选择更优孩子： 若右孩子存在（child + 1 < n）且右孩子值更小（arr[child] >

arr[child + 1]），则child更新为右孩子索引。

比较父节点与选中的孩子：

若arr[child] < arr[parent]（小堆不满足）：交换两者的值，更新parent =

child，重新计算child = parent * 2 + 1；

若满足arr[child] >= arr[parent]：说明堆的性质已恢复，跳出循环。

3. 循环结束，堆的性质已修复。

（4）建堆时间复杂度

分析：

第1层， 20 个结点，需要向下移动h-1层；

第2层， 21 个结点，需要向下移动h-2层；

第3层， 22 个结点，需要向下移动h-3层；

第4层， 23 个结点，需要向下移动h-4层；

......

第h-1层， 2h-2 个结点，需要向下移动1层。

则需要移动结点总的移动步数为：每层结点个数 * 向下调整次数。

这里同样使用错位相减来推导：

①

②

②-①，错位相减，可以得到：

根据二叉树的性质可以知道：和，带入上式可得：

故向下调整算法建堆时间复杂度为： 。

2.3.6 HPPop( )函数（出堆）

（1）实现逻辑

1. 合法性校验： 通过assert(!HPEmpty(php))确保堆非空（避免删除空堆的非法操作）。

2. 交换堆顶与堆尾元素： 将堆顶元素（数组索引为0）与堆的最后一个元素（数组索引为size-1）交换 ------ 这是为了避免直接删除堆顶导致完全二叉树结构断裂。

3. 缩小堆的范围： 将size减 1，相当于**"逻辑删除" 原堆顶元素** （此时原堆顶元素已被交换到数组末尾，size减 1 后不再被视为堆的有效元素）。

4. 维护堆性质： 调用AdjustDown函数，从新的堆顶（原堆尾元素）开始向下调整，确保调整后堆仍满足小堆或大堆的性质。

完整代码如下：

bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

void HPPop(HP* php)
{
	assert(!HPEmpty(php));
	Swap(&php->arr[0], &php->arr[php->size - 1]);
	--php->size;
	//堆顶数据需要向下调整
	AdjustDown(php->arr, 0, php->size);
}

（2）底层原理

为什么我们不直接删除堆顶呢？

堆是一种完全二叉树若直接删除堆顶（索引为0），数组后续元素需向前移动填补空位，会破坏完全二叉树的父子节点索引关系（比如原索引1的左孩子会变成新堆顶，导致结构混乱），且时间复杂度会从退化到。而 交换堆顶与堆尾 + 缩小size 的方式，既能通过size减 1 快速 "移除" 堆顶（无需移动大量元素），又能保持完全二叉树的结构完整性。

为什么我们需要利用AdjustDown呢？

在交换之后，新堆顶是原堆尾的元素（原堆尾是叶子结点，值大概率是不满足堆的父结点性质的，比如在小堆中新堆顶可能远远大于子结点），会破坏堆的核心性质。AdjustDown能够通过 "自顶向下" 的比较交换，让新堆顶找到合适的位置，重新满足 "父节点≤子节点（小堆）" 或 "父节点≥子节点（大堆）" 的规则。

（3）应用示例

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

// 堆结构体定义
typedef int HPDataType;
typedef struct {
    HPDataType* arr;
    int size;
    int capacity; // 原代码拼写错误修正为capacity
} HP;

// 辅助函数声明（假设已实现）
void HPInit(HP* php);
void HPPush(HP* php, HPDataType x);
void AdjustDown(HPDataType* arr, int parent, int n);
void Swap(int* x, int* y);
void HPDesTroy(HP* php);

// HPEmpty函数（判断堆是否为空）
bool HPEmpty(HP* php) {
    assert(php);
    return php->size == 0;
}

// HPPop函数（当前分析函数）
void HPPop(HP* php) {
    assert(!HPEmpty(php));
    Swap(&php->arr[0], &php->arr[php->size - 1]);
    --php->size;
    AdjustDown(php->arr, 0, php->size);
}

// 主函数示例：模拟优先级队列（小堆，每次取最小值）
int main() {
    HP heap;
    HPInit(&heap);

    // 向堆中插入元素
    HPPush(&heap, 5);
    HPPush(&heap, 2);
    HPPush(&heap, 7);
    HPPush(&heap, 1); // 小堆堆顶为1
    HPPush(&heap, 3);

    // 循环删除堆顶（每次获取最小值）
    while (!HPEmpty(&heap)) {
        printf("删除的堆顶元素：%d\n", heap.arr[0]); // 依次输出1、2、3、5、7
        HPPop(&heap);
    }

    HPDesTroy(&heap);
    return 0;
}

以上的示例其实本质上是实现了一个优先级队列 ，HPPop负责 "出队"（获取并删除优先级最高的元素），HPPush负责 "入队"。

注：优先级队列的元素是按照优先级顺序而非插入顺序进行管理的。每个元素附带一个优先级值，高优先级元素先出队，同优先级元素可能遵循先进先出规则或其它策略。

（4）执行流程

下面我们以小堆[1, 2, 7, 5, 3]（size=5，capacity≥5）为例，来简要分析一下删除堆顶的执行流程，如下所示：

1. 合法性校验 ：调用HPEmpty(&heap)，返回false（堆非空），通过assert。

2. 交换堆顶与堆尾 ：交换arr[0]（1）和arr[4]（3），此时数组变为[3, 2, 7, 5, 1]。

3. 缩小堆范围 ：size从 5 减为 4，堆的有效元素为前 4 个（[3, 2, 7, 5]），原堆顶元素 1 被 "逻辑删除"（不再属于堆的一部分）。

4. 向下调整（AdjustDown）：

• 初始parent=0（值 3），左孩子child=1（值 2），右孩子child+1=2（值 7）。
• 选择更小的孩子： 右孩子 7 > 左孩子 2，故child=1。
• 比较父节点与孩子： 3>2（小堆不满足），交换arr[0]和arr[1]，数组变为[2, 3, 7, 5]。
• 更新parent=1，计算新child=1*2+1=3（值 5），此时child=3不小于size=4，循环结束。

5. 函数返回 ：堆调整为[2, 3, 7, 5]（小堆性质恢复），可进行下一次HPPop。

---

总结

本期博客中，博主带大家学习了关于顺序结构二叉树------堆的概念、结构以及相关逻辑的实现。下一期博主将为大家介绍一些有关于堆的经典应用场景，请大家多多关注！