目录

1.摘要
城市河流生态系统的保护是可持续水资源管理的关键环节,传统水质采样方法依赖船只,存在效率低、成本高及潜在污染等问题。本文提出一种创新解决方案:通过卡车与无人机协同作业,无人机负责采集水样本,卡车作为移动补给站以扩展其航程。研究建立了混合整数二次规划模型,综合考虑无人机载重变化对能耗的影响,并开发了一种改进NSGA-II,引入迭代前沿优化策略与三种专用遗传算子,以提升路径协同规划的多样性与种群质量。
2.问题描述
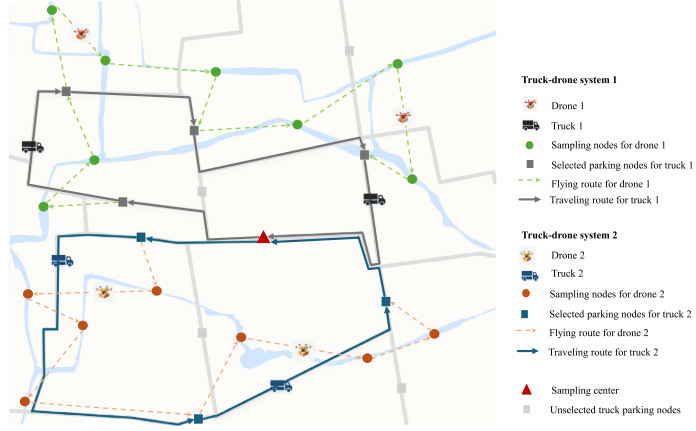
本文将一个卡车与一个无人机的组合定义为卡车-无人机系统,系统最大可用数量记为 ∣ K ∣ |K| ∣K∣。每个采样节点仅分配给一个系统,任务分配后,所有系统同时从采样中心出发:卡车作为移动补给站在道路网络行驶,无人机则负责飞往指定河道节点采集水样。无人机在电量耗尽前会飞至卡车停靠点汇合,以移交样本、更换电池。
数学模型
本文考虑最小化总运营成本和总采样完工时间,运营成本包括所有无人机飞行能耗成本,以及所有卡车行驶成本和固定使用成本,系统 k k k中卡车的行驶成本:
c o s t t k = ∑ l , j ∈ V t d i j y l j k c 1 + c 3 , ∀ k ∈ K \mathrm{cost}t^k=\sum{l,j\in V_t}d_{ij}y_{lj}^kc_1+c_3,\quad\forall k\in K costtk=l,j∈Vt∑dijyljkc1+c3,∀k∈K
能耗成本:
cost d k = ∑ l , j ∈ V d ∪ V t W i j U x i j k c 2 , ∀ k ∈ K \operatorname{cost}d^k=\sum{l,j\in V_d\cup V_t}W_{ij}^Ux_{ij}^kc_2,\quad\forall k\in K costdk=l,j∈Vd∪Vt∑WijUxijkc2,∀k∈K
目标函数:
f 1 = min ∑ k ∈ K ( cost t k + cost d k ) f_1=\min\sum_{k\in K}\left(\operatorname{cost}_t^k+\operatorname{cost}d^k\right) f1=mink∈K∑(costtk+costdk)
f 2 = min ( max k ∈ K { max { t k U , D , t k G , D } } ) f_2=\min\left(\max{k\in K}\left\{\max\left\{t_k^{U,D},t_k^{G,D}\right\}\right\}\right) f2=min(k∈Kmax{max{tkU,D,tkG,D}})
3.算法
本节提出了用于解决多卡车-无人机系统河流采样路径问题的NSGA-II-IFO(带迭代前沿优化的非支配排序遗传算法)。

初始解
初始种群的质量直接影响搜索效率与解的多样性。算法首先设定随机种群规模并计算最大系统数,再随机确定系统数量并分配采样与停车节点;在此基础上先生成无人机路径,再插入卡车停车点以形成协同路线,并据此计算成本与完成时间生成染色体。完成后去除重复解,结合非支配排序与拥挤度更新种群,并修复前沿解;最终依据等级和拥挤度选取优质个体作为父代,进而通过遗传操作产生初始子代。

卡车-无人机系统检查与修复策略
在解构建过程中,随机选择系统数量会导致不同配置下解的差异性,部分系统可能因表现较差而在非支配排序中被排除,从而削弱后续搜索的多样性。为避免此问题,提出检查与修复策略:在每次迭代中遍历当前帕累托前沿的系统配置,若存在缺失则补充构造相应解并加入前沿,直至所有系统均具备对应的最优解集,确保解集完整性与多样性。

迭代前沿优化
为构建缺失系统的解集,采用NSGA-II框架生成初始随机种群并去重,经遗传操作得到初始子代。在迭代过程中,当前父代与子代合并后进行非支配排序,选取前 m m m个个体作为新父代,并继续进行遗传操作以产生新子代。该过程持续至达到最大迭代次数,最终输出缺失系统的帕累托前沿。

解的表示
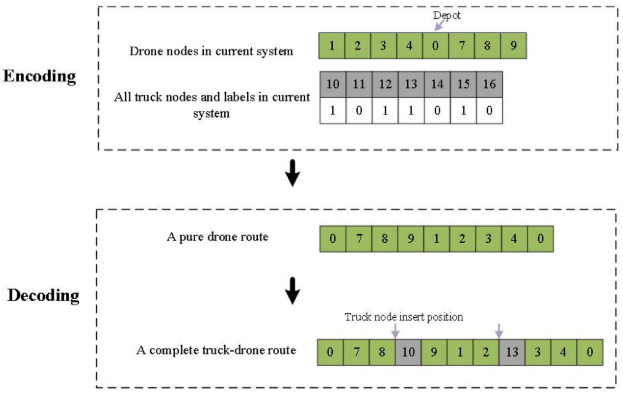
解的构建包括编码与解码两个阶段。编码阶段中,采样节点与分配的采样中心被确定,并随机生成部分卡车停车节点,已选节点记为 1,未选节点记为 0。解码阶段分为两步:首先,将标记为 0 的采样中心固定在当前无人机采样序列中,依次排列前后节点,形成纯无人机路径。随后,将卡车停车节点按最优插入位置依次加入路径,以最小化总行驶距离,从而得到完整的卡车-无人机协同路径。
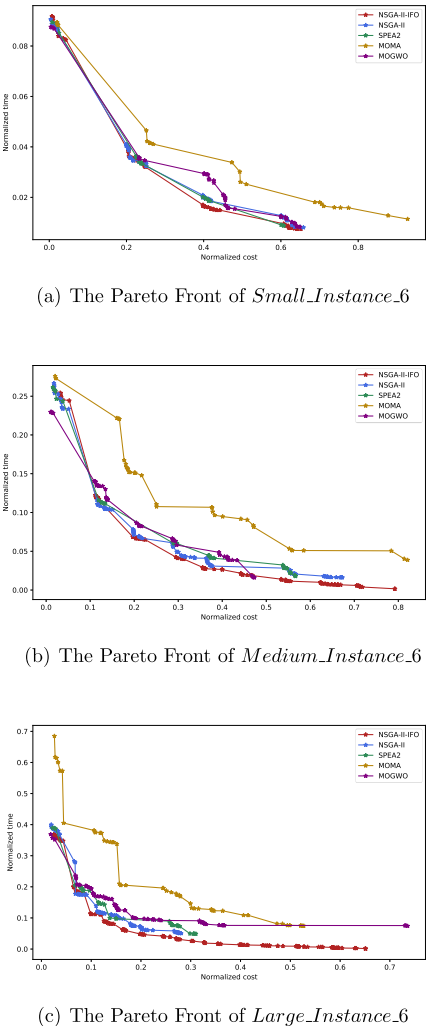
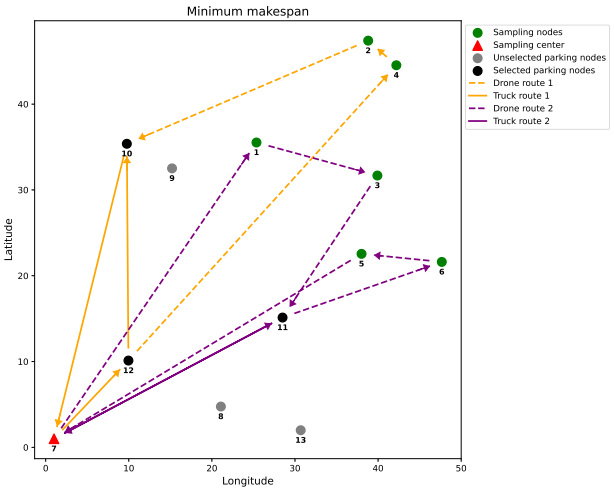
4.结果展示
5.参考文献
1\] Dang S, Luo Z, Liu Z, et al. A bi-objective routing problem for cooperated trucks and drones in river water quality monitoring\[J\]. Swarm and Evolutionary Computation, 2025, 98: 102148. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx