本文主要针对于二元 LDPC码进行展开论述，一个二元 LDPC码由对应GF(2)域上的校验矩阵H 确定，校验矩阵H 与LDPC 码的码字c 有着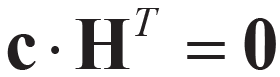
的校验关系。
在校验矩阵H 中，每行中"1"的总数称为该校验矩阵的行重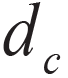
，每列中"1"的总数称为该校验矩阵的列重
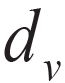，行重和列重恒定不变的LDPC码称为规则LDPC码。对于一个 LDPC码来说，常用(n, k)来表示，其中n表示码长，k表示信息序列的长度，该LDPC 码的码率为：
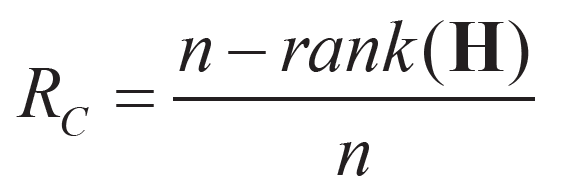
其中rank(H )为校验矩阵的秩，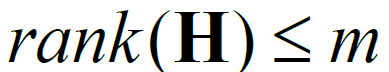
。若 LDPC码的校验矩阵H 满秩，则码率
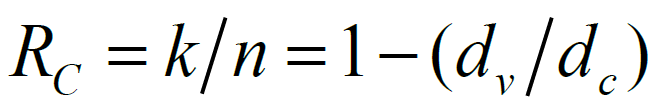，反之则码率
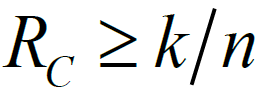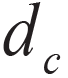。以行重 为4，列重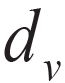为2 的(10,5)规则LDPC码为例，其校验矩阵H 及
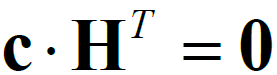的关系如下式所示。
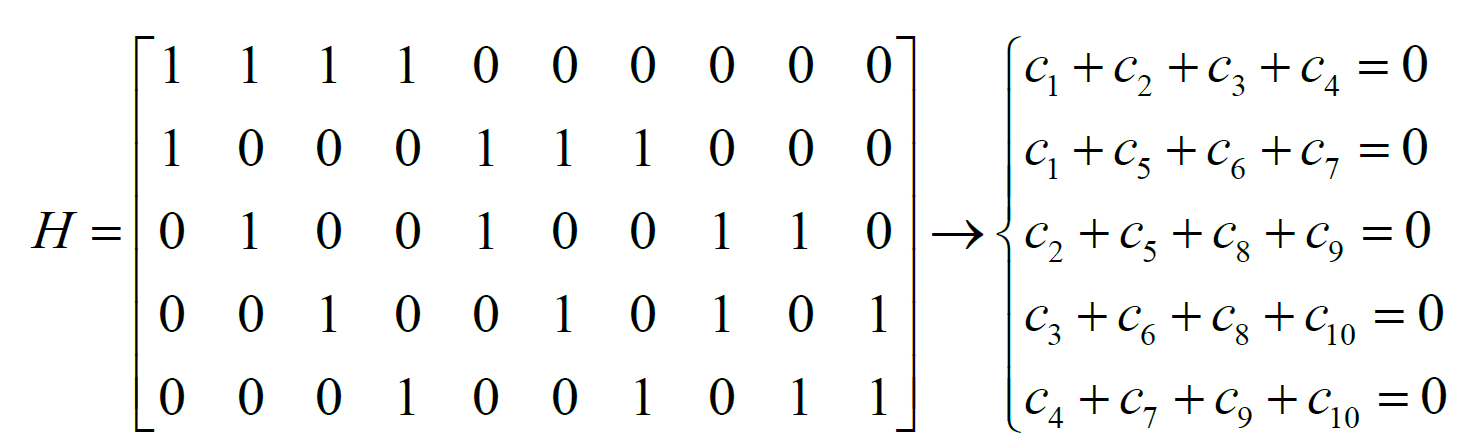
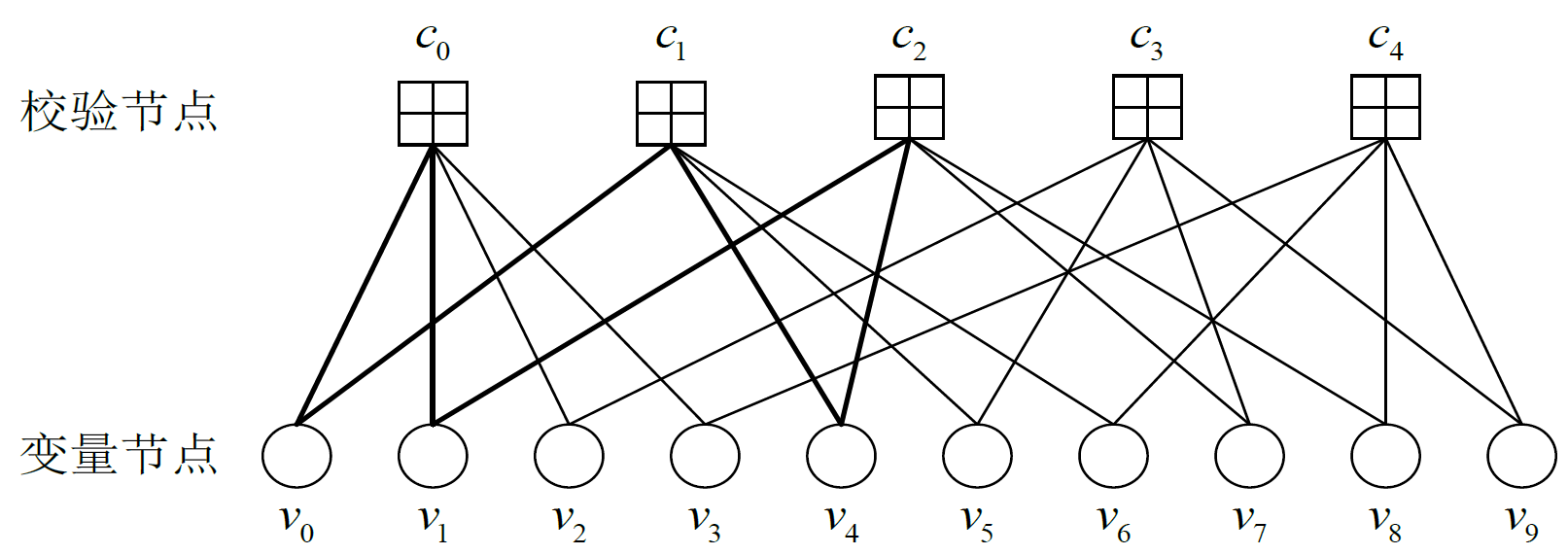
LDPC 码可以通过Tanner 图的方式来表示，Tanner 图由变量和校验两类节点组成，两节点间通过边连接，每条边只能用于连接两种不同类型节点，每个节点上边的总数称为该节点的度。
对于大小为mXn的二维校验矩阵H ，使用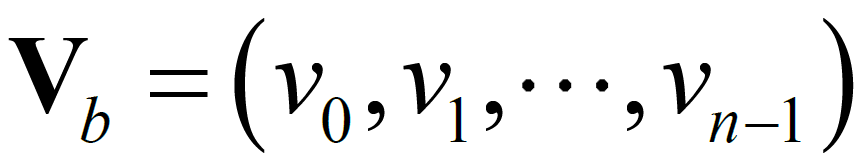
表示变量节点，使用
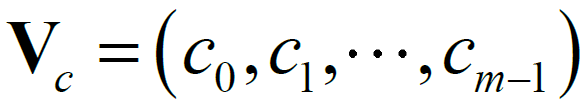表示校验节点。若H(i, j) =1，则在 Tanner图中第i 个校验节点和第j 个变量节点相连，即存在一条连接校验节点i 和变量节点j 的边。
