本文为大家介绍3D Gaussian Splatting。3D Gaussian Splatting 是一种新兴的三维场景表示与渲染技术,近年来因其高质量、高效率的实时渲染能力而受到广泛关注。该方法将三维场景建模为大量具有空间位置、协方差(控制形状与方向)、不透明度和球谐系数的高斯椭球体(Gaussians)。在渲染过程中,这些高斯体被"投射"(即splatting)到图像平面上,通过可微分的光栅化过程合成最终图像。
与传统的神经辐射场(NeRF)等隐式表示方法不同,3D Gaussian Splatting 采用显式几何表示,避免了训练过程中对神经网络的依赖,从而显著提升了渲染速度,甚至可在消费级GPU上实现实时高质量新视角合成。此外,该方法支持高效的优化策略,例如基于梯度的密度控制(克隆、分裂或删除高斯体),以适应场景复杂度并提升重建精度。
自2023年提出以来,3D Gaussian Splatting 已成为三维重建与图形学领域的重要研究方向,广泛应用于虚拟现实、数字孪生、影视特效和机器人感知等场景。
1 高斯球投影
在3DGS的初始阶段,算法会将输入的3D点云中的每一个点,直接初始化为一个高斯球。物体的高斯球所在的坐标系被称为局部坐标系。高斯球的参数包括高斯球在局部坐标系下的缩放sx,sy,szs_x, s_y, s_zsx,sy,sz,高斯球在世界坐标系下的位置μw∈R3\boldsymbol\mu_{w}\in\mathbb{R}^3μw∈R3,四元数表示的从局部坐标系到世界坐标系的旋转qwl∈R4\mathbf{q}_{wl}\in\mathbb{R}^4qwl∈R4,不透明度αraw\alpha^{\text{raw}}αraw和球谐系数若干。这些量具有可微属性,可以被神经网络优化。
将缩放参数和旋转参数写成矩阵形式,得到缩放矩阵
S=diag(sx,sy,sz) \mathbf{S}=\mathrm{diag}(s_x, s_y, s_z) S=diag(sx,sy,sz)
和旋转矩阵
R=Rot(qwl) \mathbf{R}=\mathrm{Rot}(\mathbf{q}_{wl}) R=Rot(qwl)
组合旋转和缩放,得到
M=RS \mathbf{M} = \mathbf{R}\mathbf{S} M=RS
最终得到的世界坐标系中的协方差矩阵为
Σ=MMT=RSSTRT \boldsymbol{\Sigma} = \mathbf{M}\mathbf{M}^T = \mathbf{R}\mathbf{S}\mathbf{S}^T\mathbf{R}^T \quad Σ=MMT=RSSTRT
该协方差矩阵描述了高斯球在世界坐标系下的形状和朝向
有了世界坐标系下的3DGS表示,可以根据相机内外参得到高斯球投影到像素平面后的椭圆位置,形状和朝向,投影后的椭圆整体被称为splat
考虑一个高斯球,其参数如上文所述,首先使用相机外参,将高斯球上的点xw\mathbf{x}{w}xw转换为相机坐标系下的点xc\mathbf{x}{c}xc
xc=φ(xw)=Wcwxw+dcwc \mathbf{x}{c}=\varphi(\mathbf{x}{w})=\mathbf{W}{cw}\mathbf{x}{w}+\mathbf{d}^{c}_{cw} xc=φ(xw)=Wcwxw+dcwc
设xc=[xc,yc,zc]T\mathbf{x}{c}=[x_c,y_c,z_c]^Txc=[xc,yc,zc]T,则其到投影像素xp\mathbf{x}{p}xp的变换为
xp=P(xc)=1Z[fx0cx0fycy][XYZ] \mathbf{x}{p}=\mathcal{P}(\mathbf{x}{c})= \frac{1}{Z}\left[ \begin{array}{ccc} f_{x}&0&c_{x}\\ 0&f_{y}&c_{y} \end{array} \right] \left[ \begin{array}{ccc} X\\Y\\Z \end{array} \right] xp=P(xc)=Z1[fx00fycxcy] XYZ
然而,P\mathcal{P}P并不是仿射的,要计算高斯球投影到二维像素平面上的形状,只能将其在高斯球的中心点μc=φ(μw)=[xcμ,ycμ,zcμ]T\boldsymbol\mu_{c}=\varphi(\boldsymbol{\mu}{w})=[x^{\mu}c,y^{\mu}c,z^{\mu}c]^Tμc=φ(μw)=[xcμ,ycμ,zcμ]T处进行泰勒展开
xp≈P(μc)+J(Wcwxw+dcwc−μc) \mathbf{x}{p}\approx\mathcal{P}(\boldsymbol\mu{c})+\mathbf{J}(\mathbf{W}{cw}\mathbf{x}{w}+\mathbf{d}^{c}{cw}-\boldsymbol\mu{c}) xp≈P(μc)+J(Wcwxw+dcwc−μc)
其中μp=P(μc)\boldsymbol\mu_{p}=\mathcal{P}(\boldsymbol\mu_{c})μp=P(μc)表示高斯球投影后的椭圆的位置,而
J=∂P(xc)∂xc∣xc=μc=[fxzcμ0−cxzcμzcμ20fyzcμ−cyzcμzcμ2] \mathbf{J}=\left.\frac{\partial\mathcal{P}(\mathbf{x}{c})}{\partial\mathbf{x}{c}}\right|{\mathbf{x}{c}=\boldsymbol\mu_{c}}=\begin{bmatrix} \frac{f_{x}}{z^{\mu}c}&0&-\frac{c{x}}{z^{\mu}_c\vphantom{z^{\mu}c}^2}\\ 0&\frac{f{y}}{z^{\mu}c}&-\frac{c{y}}{z^{\mu}_c\vphantom{z^{\mu}_c}^2} \end{bmatrix} J=∂xc∂P(xc) xc=μc=[zcμfx00zcμfy−zcμzcμ2cx−zcμzcμ2cy]
故世界坐标系下高斯球的协方差矩阵Σ\boldsymbol{\Sigma}Σ,在像素坐标系下对应的二维协方差矩阵Σ′\boldsymbol\Sigma^{\prime}Σ′为
Σ′=JWcwΣWcwTJT \boldsymbol\Sigma^{\prime}=\mathbf{J}\mathbf{W}{cw}\boldsymbol\Sigma\mathbf{W}{cw}^{T}\mathbf{J}^{T} Σ′=JWcwΣWcwTJT
该协方差矩阵描述了高斯球投影后的椭圆在像素坐标系下的形状和朝向
上述高斯球在像素平面上投影后的椭圆位置,形状和朝向是整个splatting的过程的一部分,将会在后续被用到
2 球谐函数
3DGS引入了球谐函数(Spherical Harmonics, SH)来建模方向相关的颜色(view-dependent color),下面介绍球谐函数。

球谐函数是一族定义在单位球面上的基函数:
Ylm(θ,ϕ)={2Klmcos(mϕ)Plm(cosθ)m>0Kl0Pl0(cosθ)m=02Kl∣m∣sin(∣m∣ϕ)Pl∣m∣(cosθ)m<0 Y^m_{l}(\theta,\phi)= \left\{\begin{array}{ll} \sqrt{2}K^{m}{l}\cos(m\phi)P^{m}{l}(\cos\theta)&m>0\\ K^{0}{l}P^{0}{l}(\cos\theta)&m=0\\ \sqrt{2}K^{|m|}{l}\sin(|m|\phi)P^{|m|}{l}(\cos\theta)&m<0 \end{array}\right. Ylm(θ,ϕ)=⎩ ⎨ ⎧2 Klmcos(mϕ)Plm(cosθ)Kl0Pl0(cosθ)2 Kl∣m∣sin(∣m∣ϕ)Pl∣m∣(cosθ)m>0m=0m<0
其中l⩾0l\geqslant0l⩾0表示阶数(degree),−l⩽m⩽l-l\leqslant m \leqslant l−l⩽m⩽l表示次序,θ,ϕ\theta,\phiθ,ϕ表示球坐标中的极角和方位角,而
Pn(x)=12n⋅n!dndxn[(x2−1)n]Plm(x)=(−1)m(1−x2)m2dmdxmPl(x)Klm=(2l+1)(l−∣m∣)!4π(l+∣m∣)! \begin{align*} P_n(x)&=\frac{1}{2^n\cdot n!}\frac{d^n}{d x^n}[(x^2-1)^n]\\ P^m_l(x)&=(-1)^m(1-x^2)^{\frac{m}{2}}\frac{d^m}{d x^m}P_l(x)\\ K^m_l&=\sqrt{\frac{(2l+1)(l-|m|)!}{4\pi(l+|m|)!}} \end{align*} Pn(x)Plm(x)Klm=2n⋅n!1dxndn[(x2−1)n]=(−1)m(1−x2)2mdxmdmPl(x)=4π(l+∣m∣)!(2l+1)(l−∣m∣)!
将基函数可视化出来,可以发现,随着阶数的增加,波瓣的数量越来越多,即空间频率越来越大,不同的阶数可以建模不同层次的场景结构,若低阶更基函数更倾向于建模整体亮度或平均颜色,而高阶基函数更倾向于建模边缘,复杂材质等细粒度细节
在3DGS里,固定视角下,R,G,B三个通道的颜色都可以各自计算为
C(ρ)=∑l=0L∑m=−llcl,mYlm(θ(ρ),ϕ(ρ)) C(\boldsymbol\rho)=\sum_{l=0}^{L}\sum_{m=-l}^{l}c_{l,m}Y^m_{l}(\theta(\boldsymbol\rho),\phi(\boldsymbol\rho)) C(ρ)=l=0∑Lm=−l∑lcl,mYlm(θ(ρ),ϕ(ρ))
其中LLL是3DGS所采取的球谐函数阶数,ρ\boldsymbol\rhoρ是视角方向,从高斯中心指向相机坐标系原点,θ,ϕ\theta,\phiθ,ϕ可以根据其计算出来,cl,mc_{l,m}cl,m是可学习的球谐系数,用来编码场景在不同视角下的颜色分布,容易得到,每个高斯球对应的球谐系数有(L+1)2×3(L+1)^2\times3(L+1)2×3。需要注意,在球谐函数的阶数越高,表示颜色随视角变化的细节能力越强,但会显著增加存储开销和计算负担,并且大多数自然场景的视角相关颜色变化集中在L⩽3L\leqslant3L⩽3,L>3L>3L>3带来的视觉提升往往不明,因此默认使用L=3L=3L=3,在质量、效率、稳定性之间取得最佳平衡
3 渲染
在 3D Gaussian Splatting 中,渲染可以被定义为:将用多个参数化高斯分布表示的三维场景转化为二维图像的技术,该过程涉及到对这些高斯分布进行光栅化处理,根据它们在屏幕空间中的覆盖范围和相对深度排序,执行α-blending操作以合成最终的像素颜色值。
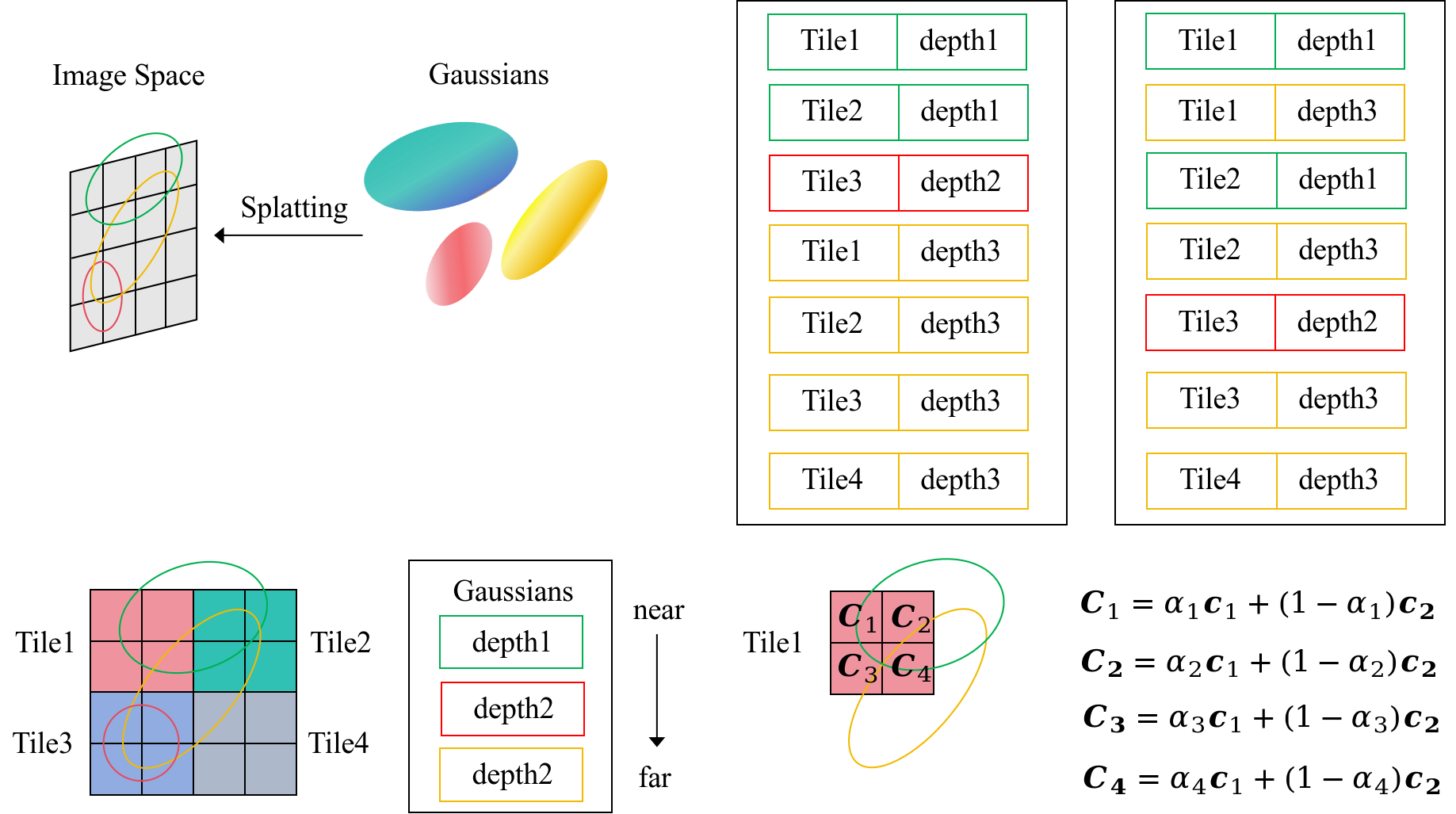
为了兼顾渲染质量和计算效率,在3DGS的渲染通过光栅化方式实现:首先,对所有待渲染的Gaussians进行一次全局深度(Gaussians中心点在相机坐标系下的z值)排序,而非在每个像素上独立排序。具体来说,系统根据高斯中心在当前相机视角下的深度值,对整个场景中的高斯列表进行一次front-to-back(按距离相机中心深度由近及远)排序。这样,在后续光栅化阶段,每个像素所访问的高斯序列天然保持正确的深度顺序,避免了为每个像素重复执行排序操作,从而大幅降低了排序带来的计算开销,尤其在高分辨率图像和密集高斯场景下效果显著。其次,渲染过程以tile(例如 16×16 像素的子区域)为基本处理单元,对于每个tile,从全局有序列表中筛选出覆盖该tile的Gaussians。由于全局列表已经按深度排好序,tile内的Gaussians顺序可以直接继承,无需重新排序。与此同时,每个Gaussian的投影坐标、协方差矩阵、屏幕半径等属性在预处理阶段只需计算一次,结果可供所有覆盖的tile和像素共享,从而避免冗余计算。在算法实现中,底层代码仅处理单个像素,因为不仅各tile之间可以并行,tile内部的各像素间也可以并行处理,这显著加快了渲染速度
下面展示单个像素的RGB值计算。点xp\mathbf{x}{p}xp处的颜色值为
C=∑i=1NαiciTi \mathbf{C}=\sum{i=1}^{N}\alpha_{i}\mathbf{c}{i}T{i} C=i=1∑NαiciTi
其中i=1,⋯ ,Ni=1,\cdots,Ni=1,⋯,N表示tile内部splats按深度从前到后的排序,ci\mathbf{c}{i}ci表示RGB三通道的颜色值,αi\alpha{i}αi表示该点处的不透明度,其由可学习的原始不透明度和权重相乘得到
αi=αirawexp(−12(xp−μp,i)TΣi′(xp−μp,i)) \alpha_{i}=\alpha_{i}^{\text{raw}}\exp\left(-\frac{1}{2}(\mathbf{x}{p}-\boldsymbol\mu{p,i})^T\boldsymbol\Sigma^{\prime}{i}(\mathbf{x}{p}-\boldsymbol\mu_{p,i})\right) αi=αirawexp(−21(xp−μp,i)TΣi′(xp−μp,i))
TiT_{i}Ti表示第iii点之前,光线没有被阻挡的概率,又称为透射率,其可以写成
Ti=∏j=1i−1(1−αj) T_{i}=\prod_{j=1}^{i-1}(1-\alpha_{j}) Ti=j=1∏i−1(1−αj)
故整体颜色可以表示为
c=∑i=1Nαici∏j=1i−1(1−αj) c=\sum_{i=1}^{N}\alpha_{i}c_{i}\prod_{j=1}^{i-1}(1-\alpha_{j}) c=i=1∑Nαicij=1∏i−1(1−αj)
上式又称为α-blending
4 损失计算
3DGS损失函数如下
L=(1−λ)L1+λLD-SSIM L=(1-\lambda)L_{1}+\lambda L_{\text{D-SSIM}} L=(1−λ)L1+λLD-SSIM
L1L_1L1是图像重建误差,可以通过与真实图像的像素级差异计算
L1=1HW∑i=1HW∣Iipred−Iigt∣ L_1=\frac{1}{HW}\sum_{i=1}^{HW}\left|I^{\text{pred}}_i-I^{\text{gt}}_i\right| L1=HW1i=1∑HW Iipred−Iigt
设重建图像和真实图像分别为Ipred,IgtI^{\text{pred}},I^{\text{gt}}Ipred,Igt
对于彩色图像,SSIM值等于各通道SSIM值的平均
SSIM=13(SSIMR+SSIMG+SSIMB) \text{SSIM}=\frac{1}{3}(\text{SSIM}{R}+\text{SSIM}{G}+\text{SSIM}_{B}) SSIM=31(SSIMR+SSIMG+SSIMB)
为进行梯度下降优化,将相似度指标转化为D-SSIM(Dissimilarity Structural SIMilarity)损失函数
LD-SSIM=1−SSIM2 L_{\text{D-SSIM}}=\frac{1-\text{SSIM}}{2} LD-SSIM=21−SSIM
即两张图像感知差异越大,LD-SSIML_{\text{D-SSIM}}LD-SSIM越大。综上可知,λ→0\lambda\rightarrow0λ→0时,更偏向像素精确;λ→1\lambda\rightarrow1λ→1时,更偏向感知正确
通过优化3DGS 的损失函数,我们可以不断调整每个3D高斯的参数(位置、缩放、旋转、球谐系数、不透明度等),使得渲染出的图像与训练数据集中的真实视角尽可能接近。同时,模型不仅能逐步修正错误的几何结构,还能自动生成、移动或删除高斯来优化场景表示。最终,优化过程得到的是一种紧凑而高效的场景表示形式:少量各向异性(协方差矩阵非单位阵,各方向色彩不同)高斯即可精确捕捉到真实世界的几何与光照特征,从而实现高质量的新视角合成与实时渲染。
附录
§1、结构相似性指标
结构相似性指标SSIM(Structural SIMilarity Index)损失函数考虑了亮度(luminance) ,对比度(contrast),结构(structure)指标,更符合人眼视觉感知,能让渲染结果纹理细节、结构对比上看起来更自然。对于但单道图像x,y\mathbf{x},\mathbf{y}x,y,有
SSIM=[l(x,y)]α[c(x,y)]β[s(x,y)]γ \text{SSIM}=\left[l(\mathbf{x},\mathbf{y})\right]^{\alpha}\left[c(\mathbf{x},\mathbf{y})\right]^{\beta}\left[s(\mathbf{x},\mathbf{y})\right]^{\gamma} SSIM=[l(x,y)]α[c(x,y)]β[s(x,y)]γ
其中α,β,γ>0\alpha,\beta,\gamma>0α,β,γ>0,l(x,y),c(x,y),s(x,y)l(\mathbf{x},\mathbf{y}),c(\mathbf{x},\mathbf{y}),s(\mathbf{x},\mathbf{y})l(x,y),c(x,y),s(x,y)分别比较x,y\mathbf{x},\mathbf{y}x,y的亮度,对比度,结构的相似性
l(x,y)=2μxμy+C1μx2+μy2+C1c(x,y)=2σxσy+C2σx2+σy2+C2c(x,y)=σxy+C3σxσy+C3 \begin{align*} l(\mathbf{x},\mathbf{y}) &=\frac{2\mu_x\mu_y+C_1}{\mu^2_x+\mu^2_y+C_1}\\ c(\mathbf{x},\mathbf{y}) &=\frac{2\sigma_x\sigma_y+C_2}{\sigma^2_x+\sigma^2_y+C_2}\\ c(\mathbf{x},\mathbf{y}) &=\frac{\sigma_{xy}+C_3}{\sigma_x\sigma_y+C_3}\\ \end{align*} l(x,y)c(x,y)c(x,y)=μx2+μy2+C12μxμy+C1=σx2+σy2+C22σxσy+C2=σxσy+C3σxy+C3
其中μx,μy,σx,σy,σxy\mu_x,\mu_y,\sigma_x,\sigma_y,\sigma_{xy}μx,μy,σx,σy,σxy是重建图像和参考图像在单个通道上的均值和标准差和协方差
实际使用时,常令α=β=γ=1\alpha=\beta=\gamma=1α=β=γ=1,C3=C22C_3=\frac{C_2}{2}C3=2C2,此时
SSIM=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2) \text{SSIM}=\frac{(2\mu_x\mu_y+C_1)(2\sigma_{xy}+C_2)}{(\mu^2_x+\mu^2_y+C_1)(\sigma^2_x+\sigma^2_y+C_2)} SSIM=(μx2+μy2+C1)(σx2+σy2+C2)(2μxμy+C1)(2σxy+C2)
SSIM值越大,代表两张图像越接近