目录
[2.1 柠檬水找零](#2.1 柠檬水找零)
[2.3 最大数](#2.3 最大数)
[2.4 K 次取反后最大化的数组和](#2.4 K 次取反后最大化的数组和)
0.0引言
从本周起,小编儿将带大家一起进入算法(^▽^)的学习当中。废话不多说,咱们从贪心走起儿😄😄😄
1.0贪心算法介绍
1.1什么是贪心算法
贪心算法(Greedy Algorithm)是一种在每一步决策时都选择当前局部最优解,并期望通过这些局部最优的积累最终得到全局最优解的算法。
咱们可以将其核心逻辑类比为"捡芝麻":遇到最大的芝麻就先捡,不考虑后面是否有更大的,只专注于当下最好的选择。但需注意的是,贪心算法并非适用于所有问题哈,大家要注意一下,仅在问题具备"贪心选择性质"(局部最优能导向全局最优)和"最优子结构"(全局最优包含子问题的最优解)时才有效,千万不要盲目使用😨
2.0例题详解(来源力扣)
2.1柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为
5美元。顾客排队购买你的产品,(按账单bills支付的顺序)一次购买一杯。每位顾客只买一杯柠檬水,然后向你付
5美元、10美元或20美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付5美元。注意,一开始你手头没有任何零钱。
给你一个整数数组
bills,其中bills[i]是第i位顾客付的账。如果你能给每位顾客正确找零,返回true,否则返回false。示例 1:
输入:bills = [5,5,5,10,20] 输出:true 解释: 前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。 第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。 第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。 由于所有客户都得到了正确的找零,所以我们输出 true。示例 2:
输入:bills = [5,5,10,10,20] 输出:false 解释: 前 2 位顾客那里,我们按顺序收取 2 张 5 美元的钞票。 对于接下来的 2 位顾客,我们收取一张 10 美元的钞票,然后返还 5 美元。 对于最后一位顾客,我们无法退回 15 美元,因为我们现在只有两张 10 美元的钞票。 由于不是每位顾客都得到了正确的找零,所以答案是 false
🚩🚩🚩算法思路:尽可能将5元晚点给找零,可以使得利益最大化(●'◡'●)
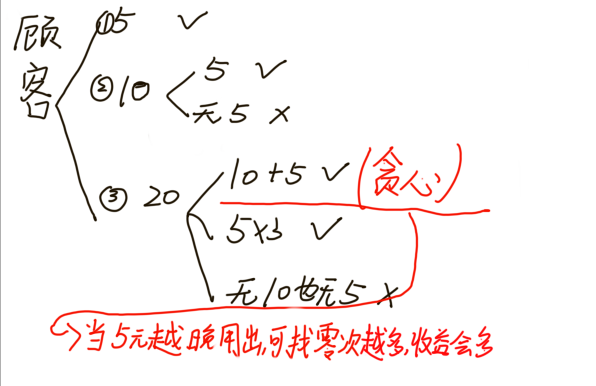
代码:
cpp
class Solution {
public:
bool lemonadeChange(vector<int>& bills) {
int five=0,ten=0;
for(int x:bills)
{
if(x==5)five++;
else if(x==10)
{
if(five)five--,ten++;
else return false;
}
else
{
if(five&&ten)five--,ten--; //贪心
else if(five-3>=0)five-=3; // ">="的'='不能丢
else return false;
}
}
return true;
}
};2.2将数组和减半的最少操作次数
给你一个正整数数组
nums。每一次操作中,你可以从nums中选择 任意 一个数并将它减小到 恰好 一半。(注意,在后续操作中你可以对减半过的数继续执行操作)请你返回将
nums数组和 至少 减少一半的 最少 操作数。示例 1:
输入:nums = [5,19,8,1] 输出:3 解释:初始 nums 的和为 5 + 19 + 8 + 1 = 33 。 以下是将数组和减少至少一半的一种方法: 选择数字 19 并减小为 9.5 。 选择数字 9.5 并减小为 4.75 。 选择数字 8 并减小为 4 。 最终数组为 [5, 4.75, 4, 1] ,和为 5 + 4.75 + 4 + 1 = 14.75 。 nums 的和减小了 33 - 14.75 = 18.25 ,减小的部分超过了初始数组和的一半,18.25 >= 33/2 = 16.5 。 我们需要 3 个操作实现题目要求,所以返回 3 。 可以证明,无法通过少于 3 个操作使数组和减少至少一半。示例 2:
输入:nums = [3,8,20] 输出:3 解释:初始 nums 的和为 3 + 8 + 20 = 31 。 以下是将数组和减少至少一半的一种方法: 选择数字 20 并减小为 10 。 选择数字 10 并减小为 5 。 选择数字 3 并减小为 1.5 。 最终数组为 [1.5, 8, 5] ,和为 1.5 + 8 + 5 = 14.5 。 nums 的和减小了 31 - 14.5 = 16.5 ,减小的部分超过了初始数组和的一半, 16.5 >= 31/2 = 15.5 。 我们需要 3 个操作实现题目要求,所以返回 3 。 可以证明,无法通过少于 3 个操作使数组和减少至少一半。
🚩🚩🚩算法思路:每次都将最大的数字除2。
代码:
cpp
class Solution {
public:
int halveArray(vector<int>& nums) {
priority_queue<double> heap;
double sum=0.0;
int count=0;
for(int x:nums)
{
heap.push(x);
sum+=x;
}
sum/=2.0;
while(sum>0) //无需等于0
{
double s=heap.top()/2.0;
heap.pop();
sum-=s;
count++;
heap.push(s);
}
return count;
}
};2.3最大数
给定一组非负整数
nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。**注意:**输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2] 输出:"210"示例 2:
输入:nums = [3,30,34,5,9] 输出:"9534330"
🚩🚩🚩算法思路:将数字转换成字符,遍历比较每一个两两组合的结果。比较'ab'和'ba'的字典数,返回结果较大的。
代码:
cpp
class Solution {
public:
string largestNumber(vector<int>& nums) {
//将数字转成字符
vector<string>strs;
for(int x:nums)strs.push_back(to_string(x));
//排序
sort(strs.begin(),strs.end(),[](const string&s1,const string&s2){return s1+s2>s2+s1;}); //贪心 tip:)不要忘
//输出
string ret;
for(auto&s:strs)ret+=s;
if(ret[0]=='0')return"0"; //1."=="不是"=",//2.若第一个字符为'0',输出"0"
return ret;
}
};2.4K 次取反后最大化的数组和
给你一个整数数组
nums和一个整数k,按以下方法修改该数组:选择某个下标
i并将nums[i]替换为-nums[i]。重复这个过程恰好
k次。可以多次选择同一个下标i。以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1 输出:5 解释:选择下标 1 ,nums 变为 [4,-2,3] 。示例 2:
输入:nums = [3,-1,0,2], k = 3 输出:6 解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2 输出:13 解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。
🚩🚩🚩算法思路:
代码:
cpp
class Solution {
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
int ret=0;int Min=INT_MAX; //这里不能用Min=nums[0],因为第一个数也可能是负数
int m=0;
for(auto x:nums)
{
if(x<0)m++;
Min=min(Min,abs(x));
}
if(m>k)
{
sort(nums.begin(),nums.end());
for(int i=0;i<k;i++)
{
ret+=-nums[i];
}
for(int i=k;i<nums.size();i++)ret+=nums[i];
}
else //当m==k时和m<k且k-m为偶数时,可以不操作,故省去。
{
for(auto x:nums)ret+=abs(x);
if((k-m)%2!=0)
{
ret-=Min*2; //Min*2因为ret+=abs(x)加过一次,现在变成负的还要在减一次
}
}
return ret;
}
};2.5最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
🚩🚩🚩算法思路:贪心思路如下,本题结合贪心和双指针可以提高运算效率,具体实现参照代码O(∩_∩)O
代码:
cpp
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int>ret;
ret.push_back(nums[0]);
for(int i=1;i<nums.size();i++)
{
if(nums[i]>ret.back())
{ ret.push_back(nums[i]);}
else //贪心+二分
{
int left=0,right=ret.size()-1;
while(left<right)
{
int mid = (left + right) /2;
if(ret[mid]<nums[i])left=mid+1;
else right=mid;
}
ret[left]=nums[i];
}
}
return ret.size();
}
};2.6摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为**摆动序列 。**第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。给你一个整数数组
nums,返回nums中作为 摆动序列 的 最长子序列的长度 。示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2
🚩🚩🚩算法思路: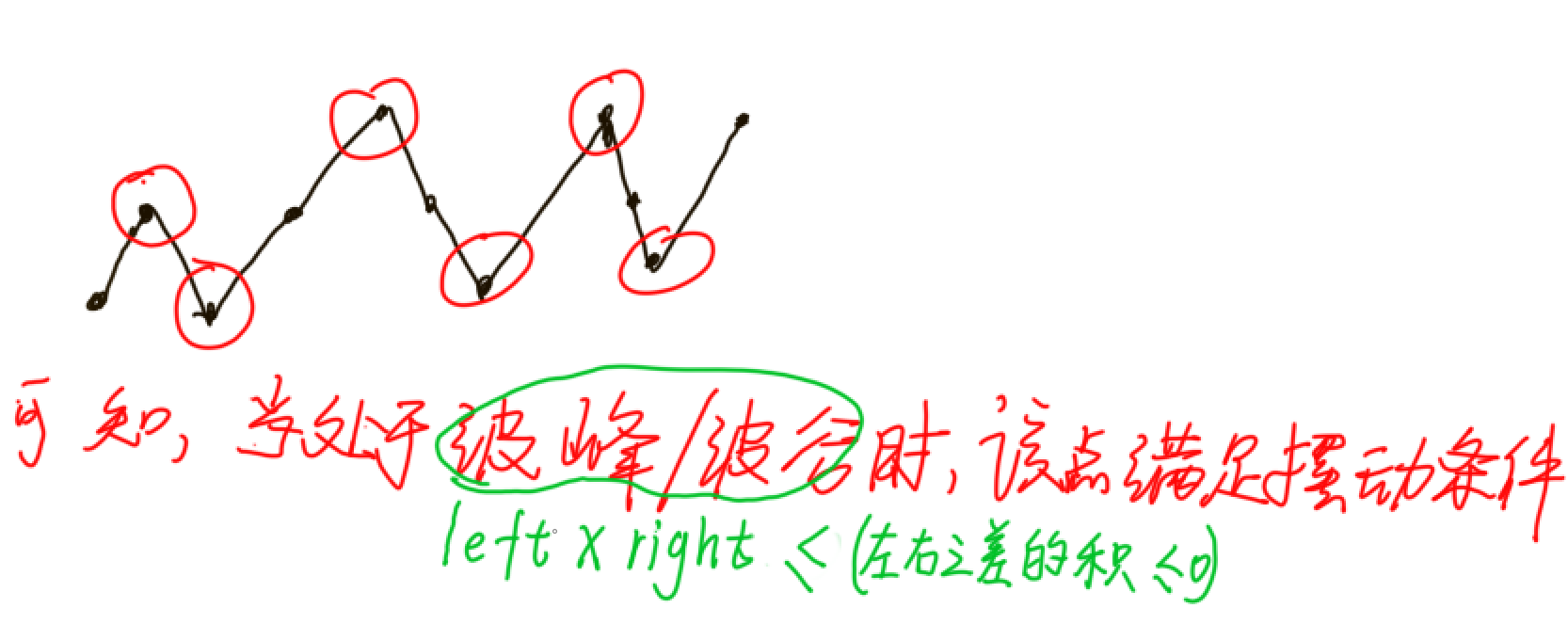
代码:
cpp
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
int left=0,right=0,ret=0;
int n=nums.size();
if(n<2)return n;
for(int i=0;i<n-1;i++)
{
right=nums[i+1]-nums[i];
if(right==0)continue; //如果是平的就跳过
if(left*right<=0)ret++; //=是为了统计第一个点
left=right;
}
return ret+1; //+1是为了加上最后一个点
}
};2.7递增的三元子序列
给你一个整数数组
nums,判断这个数组中是否存在长度为3的递增子序列。如果存在这样的三元组下标
(i, j, k)且满足i < j < k,使得nums[i] < nums[j] < nums[k],返回true;否则,返回false。示例 1:
输入:nums = [1,2,3,4,5] 输出:true 解释:任何 i < j < k 的三元组都满足题意示例 2:
输入:nums = [5,4,3,2,1] 输出:false 解释:不存在满足题意的三元组示例 3:
输入:nums = [2,1,5,0,4,6] 输出:true 解释:其中一个满足题意的三元组是 (3, 4, 5),因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6
🚩🚩🚩算法思路:
1)可以按照2.5的思路,若返回的长度值>3即成立👆👆👆
2)取第一个元素记作a,遍历数组取b(b>a),若此时还有一个数c(c>b),那么一定存在递增三元组❀
代码:
cpp
class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
int a=nums[0],b=INT_MAX;
for(int i=1;i<nums.size();i++)
{
if(nums[i]>b) return true;
else if(nums[i]>a) b=nums[i]; //贪心
else a=nums[i];
}
return false;
}
};2.8最长连续递增序列
给定一个未经排序的整数数组,找到最长且连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标
l和r(l < r)确定,如果对于每个l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。示例 1:
输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。示例 2:
输入:nums = [2,2,2,2,2] 输出:1 解释:最长连续递增序列是 [2], 长度为1。
🚩🚩🚩算法思路:本题可以使用双指针,贪心体现在i根据j的情况跳跃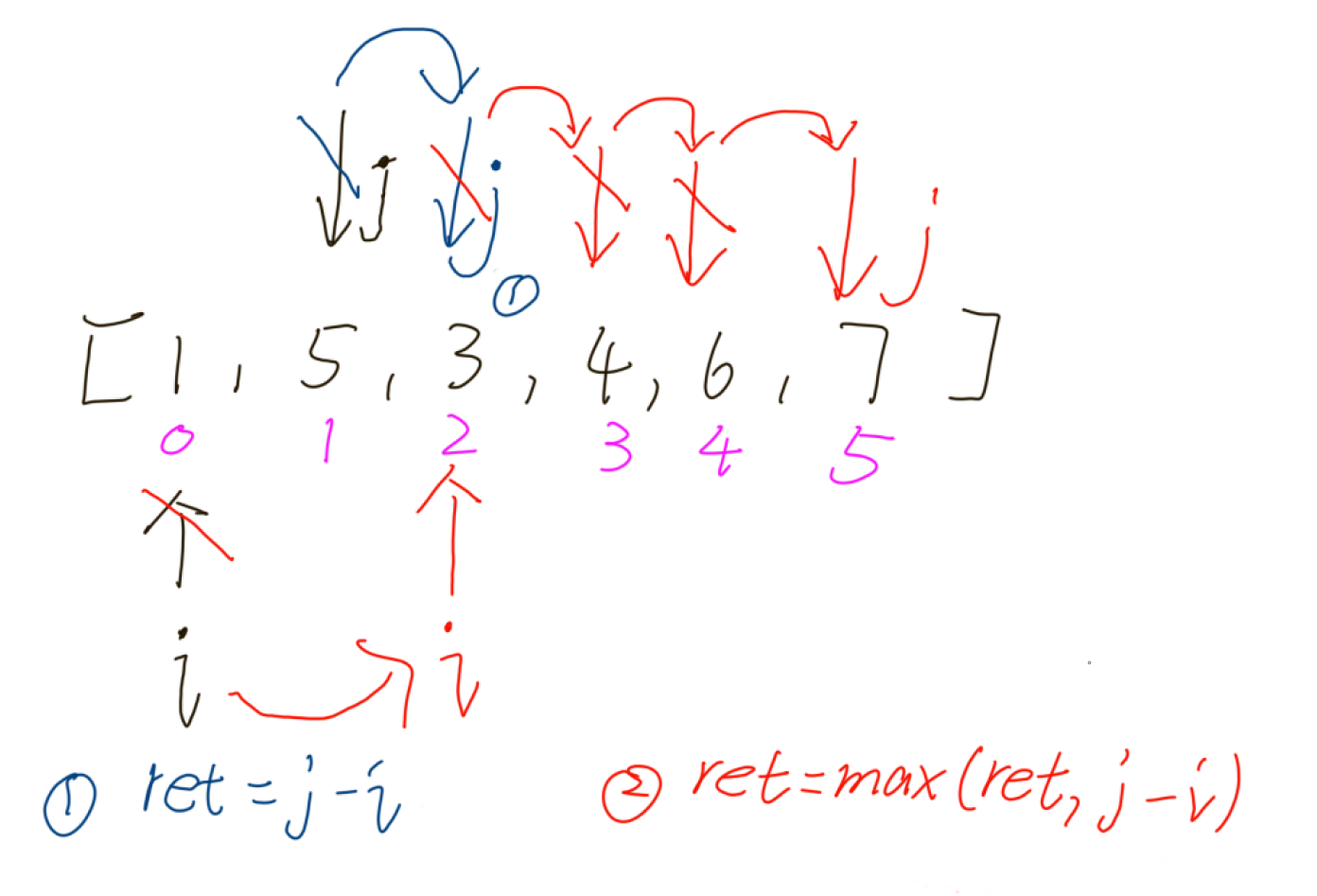
代码:
cpp
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int i=0,ret=0;
for(i=0;i<nums.size();)
{ int j=i+1; //双指针
while(j<nums.size()&&( nums[j-1]<nums[j]))j++; //j+1会越界
ret=max(ret,j-i);
i=j; //贪心
}
return ret;
}
};3.0小结
咱们通过多个力扣例题讲解了贪心算法的实际应用,包括柠檬水找零、数组和减半操作、最大数组合、K次取反求最大和、最长递增子序列、摆动序列等问题。
本周的就讲解到这里O(∩_∩)O
如果想了解更多算法题与思路,欢迎点赞收藏,咱们下周见🤭🤭🤭
