pytorch基本运算-torch.normal()函数输出多维数据时，如何绘制正态分布函数图

【1】引言

前序学习进程中，已经对使用PyTorch模块的normal()函数绘制正态分布函数图进行了初步探索。

但很显然，这里的探索只是让torch.normal()函数生成了满足正态分布的一维数据。

但实际上torch.normal()函数可以生成多维度的正态分布随机数，此时应该如何绘制随机数分布图，这就是本次学习的目标。

【2】 torch.normal()函数生成正态分布随机数

首先用torch.normal()函数生成不同维度的随机数，这里给出完整代码：

python 复制代码

# 引入模块
import torch

# 生成一维正态分布随机数
x1=torch.normal(0,1,(12,))
print('x1=',x1)

# 生成二维正态分布随机数
x2=torch.normal(0,1,(2,6))
print('x2=',x2)

# 生成三维正态分布随机数
x3=torch.normal(0,1,(2,2,3))
print('x3=',x3)

这里使用了torch.normal()函数分别生成了一维、二维和三维的正态分布随机数，由于多维数据数据确实不方便直接绘图，但我们可以抓住这些数据全部符合正态分布的特点，先将它们还原成一维数据，然后再用绘制概率密度分布图的hist()函数直接绘图。

此时代码运行，获得的随机数效果为：

x1= tensor([-2.1645, -0.4632, 1.1806, 0.0278, 0.1265, 1.4797, 0.6780, -0.4628,

-0.3890, -0.2532, -0.7040, 0.1115])

x2= tensor([[-0.8097, 1.0254, -1.8906, -0.6937, -0.1433, 0.4527],
$0.3353, -0.7879, -1.2921, 1.3192, -2.2811, -1.7203\]\]) x3= tensor(\[\[\[ 1.5328, -1.0825, 0.5024\], \[ 0.6801, -1.3820, -0.2212\]\], \[\[ 1.1011, 0.7533, -1.2041\], \[ 0.0494, 1.7353, -1.0647\]\]\])$

【3】flatten()函数将torch.normal()函数生成正态分布随机数展开为一维

flatten()函数可以直接将多维数组展平为一维，我们现在尝试将获得的正态分布随机数展平到一维。

python 复制代码

# 引入模块
import torch

# 生成一维正态分布随机数
x1=torch.normal(0,1,(12,))
print('x1=',x1)
# 展平一维随机数
data1=x1.flatten()
print('data1=',data1)
# 生成二维正态分布随机数
x2=torch.normal(0,1,(2,6))
print('x2=',x2)
# 展平二维随机数
data2=x2.flatten()
print('data2=',data2)
# 生成三维正态分布随机数
x3=torch.normal(0,1,(2,2,3))
print('x3=',x3)
# 展平三维随机数
data3=x3.flatten()
print('data3=',data3)

代码运行后的效果为：

x1= tensor([ 0.0873, -1.9582, 0.3439, -0.9570, -0.4792, 1.0583, -0.4953, 1.1465,

-1.0765, 1.2814, 0.9600, 0.1369])

data1= tensor([ 0.0873, -1.9582, 0.3439, -0.9570, -0.4792, 1.0583, -0.4953, 1.1465,

-1.0765, 1.2814, 0.9600, 0.1369])

x2= tensor([[ 0.3837, 1.6751, -0.3105, -0.4903, 2.0563, 0.4885],
$0.5631, 0.1983, -0.7726, -0.4184, 0.1417, -0.5559\]\]) data2= tensor(\[ 0.3837, 1.6751, -0.3105, -0.4903, 2.0563, 0.4885, 0.5631, 0.1983, -0.7726, -0.4184, 0.1417, -0.5559\]) x3= tensor(\[\[\[ 0.7239, 1.1062, 0.3415\], \[ 0.9239, -1.1035, -0.4100\]\], \[\[-0.0320, 0.6664, -0.2891\], \[ 0.6788, 1.5814, -1.9836\]\]\]) data3= tensor(\[ 0.7239, 1.1062, 0.3415, 0.9239, -1.1035, -0.4100, -0.0320, 0.6664, -0.2891, 0.6788, 1.5814, -1.9836\])$

【4】使用hist函数绘制torch.normal()函数生成正态分布随机数概率密度图

这时就可以用hist函数对torch.normal()函数生成正态分布随机数绘制概率密度图。

python 复制代码

# 引入模块
import torch
import matplotlib.pyplot as plt


# 生成一维正态分布随机数
x1=torch.normal(0,1,(12,))
print('x1=',x1)

# 展平一维随机数
data1=x1.flatten()
print('data1=',data1)
plt.hist(data1.numpy(),bins=30,color='navy')
# 生成二维正态分布随机数
x2=torch.normal(0,1,(2,6))
print('x2=',x2)
# 展平二维随机数
data2=x2.flatten()
print('data2=',data2)
plt.hist(data2.numpy(),bins=30,color='green')
# 生成三维正态分布随机数
x3=torch.normal(0,1,(2,2,3))
print('x3=',x3)
# 展平三维随机数
data3=x3.flatten()
print('data3=',data3)
plt.hist(data3.numpy(),bins=30,color='red')
plt.show()

此时输出的效果图为：

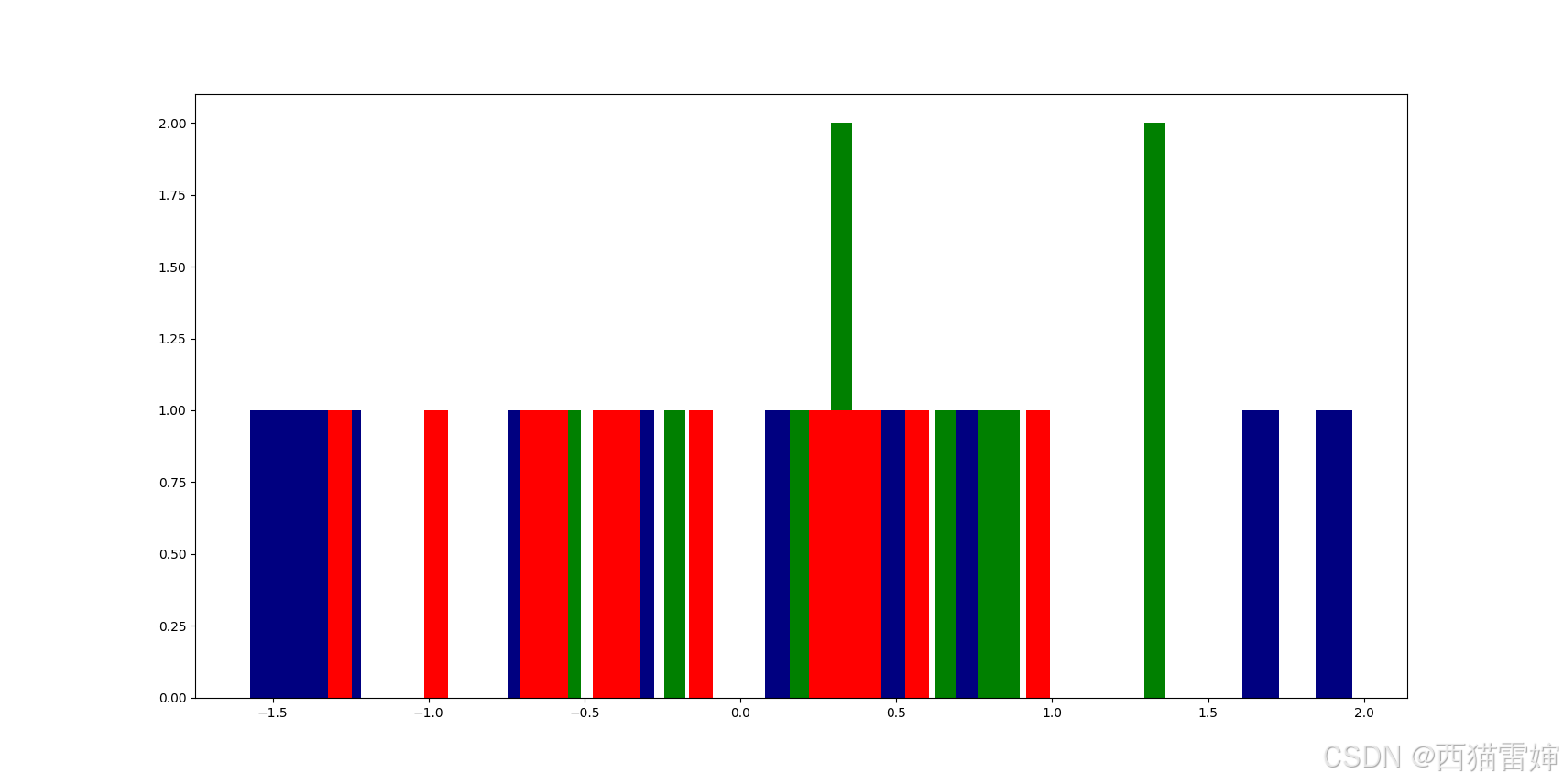
由于数据不够多，尽管已经三组数据约定了三种颜色，但这个图依然没有明显的正态分布特征。

别急，可以尝试增加随机数，最简单的，直接对第三组数据加密：

python 复制代码

# 生成三维正态分布随机数
x3=torch.normal(0,1,(20,20,30))
print('x3=',x3)
# 展平三维随机数
data3=x3.flatten()
print('data3=',data3)
plt.hist(data3.numpy(),bins=30,color='red')

之前的数据维度构成是(2,2,3)，现在加密到了(20,20,30)，看看实际效果：

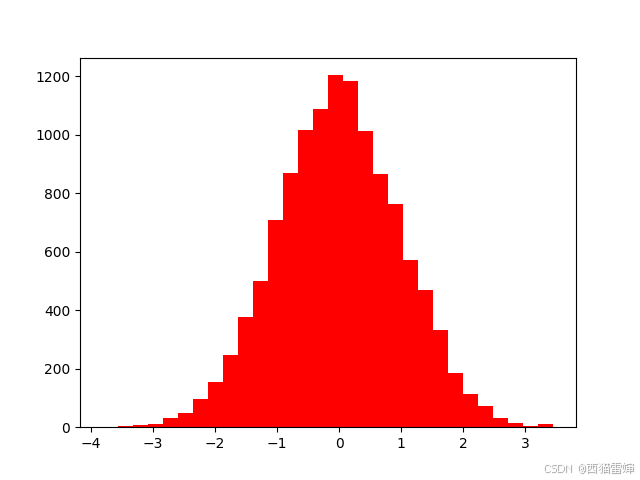
由图可见非常明显的正态分布特征。

由于数据太多，第三组数据把前两组的数据覆盖了。

此外由于代码不够精简，为此我们想办法重新写一下代码，变成优化版本。

【4】代码优化

优化后的代码具备精简和一个大图展示每组数据分布特征的优点，直接给出完整代码：

python 复制代码

# 引入模块
import torch
import matplotlib.pyplot as plt
from matplotlib.pyplot import subplots, ylabel

# 定义常数
x=[]
n=1200
for i in range(3):
    # 先定义维度
    if i==0:
        size=(n,)
    elif i==1:
        size = (20,60)
    else:
        size = (20,20,30)
    # 生成具体的随机数
    tensor=torch.normal(0,1,size=size).flatten()#.numpy()
    # x是一个空列表，使用append()函数往x中增加tensor随机数
    x.append(tensor)

# 绘图
fig,ax=subplots(3,1)
for i in range(3):
    ax[i].hist(x[i],bins=50,color=['navy', 'green', 'red'][i])
    if i == 1:  # 仅第一个子图显示y轴标签（避免重复）
        ax[i].set_ylabel('torch.normal', fontsize=12)
    if i == 2:  # 仅第二个子图显示x轴标签（避免重复）
        ax[i].set_xlabel('x', fontsize=12)

plt.show()

这里有一个重要的定义，首先约定随机数的维度：

python 复制代码

for i in range(3):
    # 先定义维度
    if i==0:
        size=(n,)
    elif i==1:
        size = (20,60)
    else:
        size = (20,20,30)
    # 生成具体的随机数
    tensor=torch.normal(0,1,size=size).flatten().numpy()

这里的size()按照维度提前定义好，所以不用每一处都单独定义。

然后是直接调用for循环沪指概率密度分布图：

python 复制代码

# 绘图
fig,ax=subplots(3,1)
for i in range(3):
    ax[i].hist(x[i],bins=50,color=['navy', 'green', 'red'][i])
    if i == 1:  # 仅第一个子图显示y轴标签（避免重复）
        ax[i].set_ylabel('torch.normal', fontsize=12)
    if i == 2:  # 仅第二个子图显示x轴标签（避免重复）
        ax[i].set_xlabel('x', fontsize=12)

这两条路逻辑很清晰，但还需要注意一个细节：

python 复制代码

    # 生成具体的随机数
    tensor=torch.normal(0,1,size=size).flatten().numpy()
    # x是一个空列表，使用append()函数往x中增加tensor随机数
    x.append(tensor)

一个是将张量数据展平，需要注意的是，plt.hist()函数和张量是兼容的，所以tensor最后是否有numpy()都可以运行。

另一个是每一个张量都要通过append()函数直接添加到空列表x中。

此时的输出效果为：

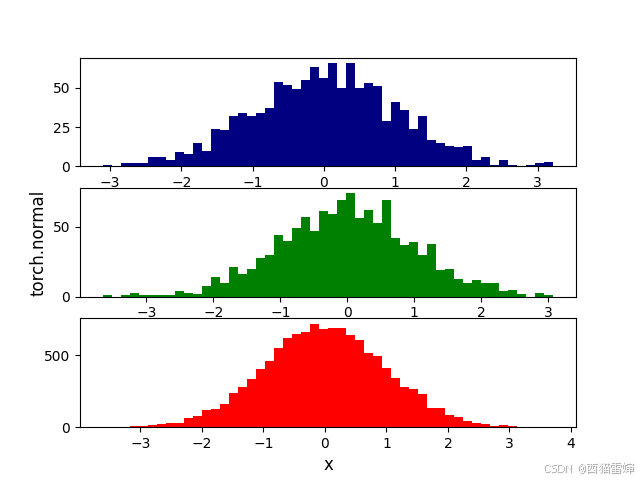
【5】总结

学习了当torch.normal()函数输出多维数据式，如何绘制正态分布函数图的基本技巧。