YOLO入门教程（番外）：卷积神经网络—图像卷积

Hcoco_me2025-10-05 17:52

上节我们解析了卷积层的原理，现在我们看看它的实际应用。由于卷积神经网络的设计是用于探索图像数据，本节我们将以图像为例。

1. 互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。 根据 6.1节中的描述，在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

首先，我们暂时忽略通道（第三维）这一情况，看看如何处理二维图像数据和隐藏表示。在 图6.2.1中，输入是高度为3、宽度为3的二维张量（即形状为3x3）。

卷积核的高度和宽度都是2，而卷积核窗口（或卷积窗口）的形状由内核的高度和宽度决定（即2x2）。

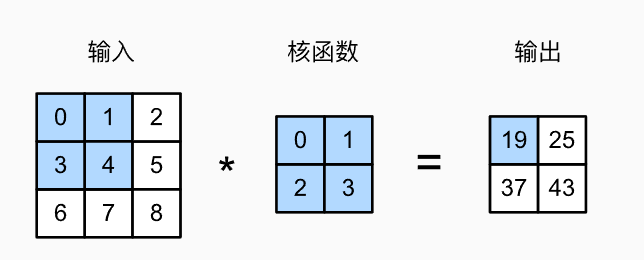
图6.2.1 二维互相关运算。阴影部分是第一个输出元素，以及用于计算输出的输入张量元素和核张量元素：

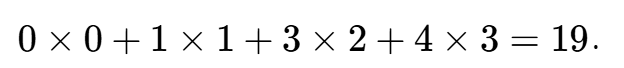
在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。

在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为2、宽度为2，如下所示：


复制代码 
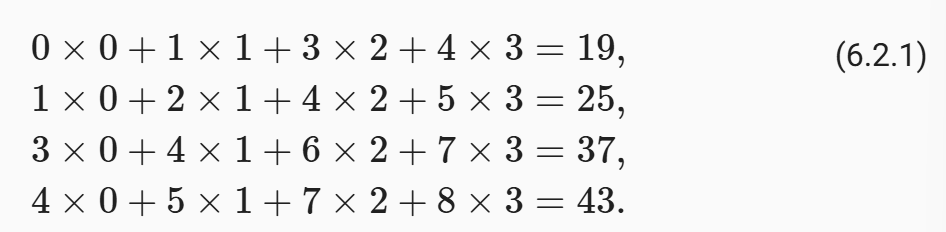
import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算
    Args:
        X: 输入张量，形状为(高度, 宽度)
        K: 卷积核张量，形状为(高度, 宽度)
    Returns:
        Y: 输出张量，形状为(X.shape[0]-K.shape[0]+1, X.shape[1]-K.shape[1]+1)
    """
    # 获取卷积核的高度和宽度
    h, w = K.shape
    
    # 初始化输出张量Y，其形状根据输入和卷积核大小计算得出
    # 高度方向: X.shape[0] - h + 1
    # 宽度方向: X.shape[1] - w + 1
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    
    # 遍历输出张量的每一个位置
    for i in range(Y.shape[0]):      # 遍历高度维度
        for j in range(Y.shape[1]):  # 遍历宽度维度
            # 计算当前位置的输出值：
            # 1. 从输入X中提取与卷积核相同大小的子区域: X[i:i+h, j:j+w]
            # 2. 将该子区域与卷积核K逐元素相乘
            # 3. 对相乘结果求和，得到当前位置的输出值
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    
    # 返回计算结果
    return Y

通过 图6.2.1的输入张量X和卷积核张量K，我们来验证上述二维互相关运算的输出。

复制代码 
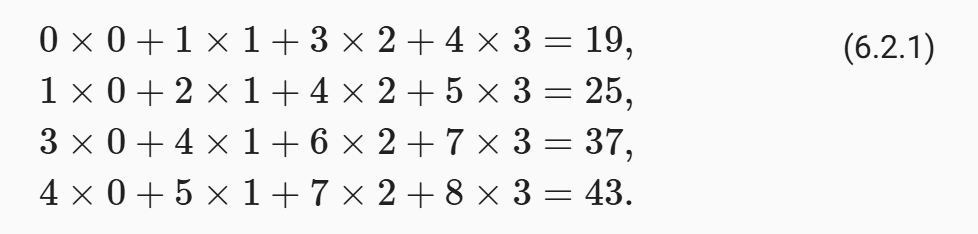
# 创建一个3x3的输入张量X，包含从0.0到8.0的9个元素
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
# 张量X的内容：
# [[0., 1., 2.],
#  [3., 4., 5.],
#  [6., 7., 8.]]

# 创建一个2x2的卷积核张量K
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
# 张量K的内容：
# [[0., 1.],
#  [2., 3.]]

# 调用corr2d函数计算X和K的二维互相关运算
corr2d(X, K)
# 计算过程：
# 1. 输出形状：根据公式 (3-2+1, 3-2+1) = (2, 2)
# 2. 计算每个输出元素：
#    Y[0,0] = X[0:2, 0:2] * K 的和 = [[0.,1.],[3.,4.]] * [[0.,1.],[2.,3.]] = (0 * 0 + 1 * 1 + 3 * 2 + 4 * 3) = 0+1+6+12 = 19.0
#    Y[0,1] = X[0:2, 1:3] * K 的和 = [[1.,2.],[4.,5.]] * [[0.,1.],[2.,3.]] = (1 * 0 + 2 * 1 + 4 * 2 + 5 * 3) = 0+2+8+15 = 25.0
#    Y[1,0] = X[1:3, 0:2] * K 的和 = [[3.,4.],[6.,7.]] * [[0.,1.],[2.,3.]] = (3 * 0 + 4 * 1 + 6 * 2 + 7 * 3) = 0+4+12+21 = 37.0
#    Y[1,1] = X[1:3, 1:3] * K 的和 = [[4.,5.],[7.,8.]] * [[0.,1.],[2.,3.]] = (4 * 0 + 5 * 1 + 7 * 2 + 8 * 3) = 0+5+14+24 = 43.0
#
# 预期输出：
# tensor([[19., 25.],
#         [37., 43.]])

tensor([[19., 25.],
        [37., 43.]])

2. 卷积层

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。

所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。 就像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。

基于上面定义的corr2d函数实现二维卷积层。

在__init__构造函数中，将weight和bias声明为两个模型参数。

前向传播函数调用corr2d函数并添加偏置。

复制代码 
# 定义一个二维卷积层类，继承自PyTorch的nn.Module基类
class Conv2D(nn.Module):
    # 初始化方法，参数kernel_size指定卷积核的尺寸（如(3,3)）
    def __init__(self, kernel_size):
        # 调用父类nn.Module的初始化方法
        super().__init__()
        # 将权重weight注册为模型参数，使用随机初始化
        # nn.Parameter表示这个张量是模型需要学习的参数
        # torch.rand(kernel_size)生成指定大小的随机张量（值在0-1之间）
        self.weight = nn.Parameter(torch.rand(kernel_size))
        # 将偏置bias注册为模型参数，初始化为0
        # 这里使用torch.zeros(1)创建一个值为0的单元素张量
        self.bias = nn.Parameter(torch.zeros(1))

    # 定义前向传播方法，描述数据如何通过该层
    def forward(self, x):
        # 计算输入x与权重weight的二维互相关运算
        # 然后加上偏置bias（会进行广播，自动扩展到与输出相同形状）
        return corr2d(x, self.weight) + self.bias

3. 图像中目标的边缘检测

如下是卷积层的一个简单应用：通过找到像素变化的位置，来检测图像中不同颜色的边缘。

首先，我们构造一个 6x8 像素的黑白图像。中间四列为黑色（0），其余像素为白色（1）。

复制代码 
X = torch.ones((6, 8))
X[:, 2:6] = 0
X



tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])

接下来，我们构造一个高度为1、宽度为2的卷积核K。当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。

复制代码 
K = torch.tensor([[1.0, -1.0]])

现在，我们对参数X（输入）和K（卷积核）执行互相关运算。 如下所示，输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘，其他情况的输出为0。

复制代码 
Y = corr2d(X, K)
Y

tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])

4. 学习卷积核

如果我们只需寻找黑白边缘，那么以上[1, -1]的边缘检测器足以。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计滤波器。那么我们是否可以学习由X生成Y的卷积核呢？

现在让我们看看是否可以通过仅查看"输入-输出"对来学习由X生成Y的卷积核。

我们先构造一个卷积层，并将其卷积核初始化为随机张量。

接下来，在每次迭代中，我们比较Y与卷积层输出的平方误差，然后计算梯度来更新卷积核。

为了简单起见，我们在此使用内置的二维卷积层，并忽略偏置。

复制代码 
# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
# nn.Conv2d是PyTorch内置的二维卷积层类
# 参数说明：
#   1: 输入通道数（灰度图像，单通道）
#   1: 输出通道数（单通道输出）
#   kernel_size=(1, 2): 卷积核尺寸为1×2（高度×宽度）
#   bias=False: 不使用偏置项
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
# 将输入X从6×8的二维张量重塑为四维张量(1, 1, 6, 8)
# 格式含义：(批量大小=1, 通道数=1, 高度=6, 宽度=8)
X = X.reshape((1, 1, 6, 8))

# 将目标输出Y重塑为四维张量(1, 1, 6, 7)
# 由于使用1×2的卷积核，输出宽度会减少1（从8变为7）
Y = Y.reshape((1, 1, 6, 7))

# 设置学习率为0.03
lr = 3e-2  # 学习率

# 进行10次训练迭代
for i in range(10):
    # 前向传播：通过卷积层计算预测输出
    Y_hat = conv2d(X)
    
    # 计算损失：使用均方误差损失函数
    # (Y_hat - Y) ** 2 计算每个元素的平方误差
    l = (Y_hat - Y) ** 2
    
    # 清零梯度：在每次反向传播前清零累积的梯度
    conv2d.zero_grad()
    
    # 反向传播：计算损失相对于所有可学习参数的梯度
    # 使用.sum()将损失张量转换为标量，然后调用.backward()计算梯度
    l.sum().backward()
    
    # 迭代卷积核：使用梯度下降更新卷积核权重
    # conv2d.weight.grad包含权重的梯度
    # lr * conv2d.weight.grad是梯度乘以学习率
    # conv2d.weight.data[:] -= ... 表示原地更新权重数据
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    
    # 每两次迭代打印一次损失
    if (i + 1) % 2 == 0:
        # 打印当前迭代次数和总损失值（保留3位小数）
        print(f'epoch {i+1}, loss {l.sum():.3f}')

这段代码演示了如何使用PyTorch内置的nn.Conv2d卷积层进行简单的训练过程：

  1. 创建卷积层：使用1×2的卷积核，不包含偏置项

  2. 数据准备：将输入和目标输出重塑为四维格式（批量大小、通道数、高度、宽度）

  3. 训练循环：进行10次迭代训练

  4. 前向传播：计算卷积层的输出

  5. 损失计算：使用均方误差作为损失函数

  6. 反向传播：计算梯度并更新卷积核权重

  7. 进度监控：每两次迭代打印一次损失值

    epoch 2, loss 6.422
    epoch 4, loss 1.225
    epoch 6, loss 0.266
    epoch 8, loss 0.070
    epoch 10, loss 0.022

在10次迭代之后，误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。

复制代码 
conv2d.weight.data.reshape((1, 2))


tensor([[ 1.0010, -0.9739]])

细心的读者一定会发现，我们学习到的卷积核权重非常接近我们之前定义的卷积核K。

解释一下conv2d.weight.data = conv2d.weight.data - (lr * conv2d.weight.grad)

python 复制代码 
conv2d.weight.data[:] -= lr * conv2d.weight.grad

这行代码是手动实现梯度下降算法来更新卷积核权重的核心语句。让我们将其分解为几个部分：

  1. conv2d.weight
  • 这是卷积层的权重参数（即卷积核本身）
  • 在PyTorch中，所有继承自nn.Module的层，其可学习参数都是nn.Parameter类型
  • 对于这个1×2的卷积核，weight的形状是(1, 1, 1, 2)（输出通道数, 输入通道数, 高度, 宽度）
  1. .data
  • weight.data获取的是参数的实际数值张量（不包含梯度计算图信息）
  • 使用.data意味着我们直接操作参数的数值，而不是通过PyTorch的自动微分系统
  1. [:]
  • 这是Python的切片语法，表示"选择所有元素"
  • 在这里，它确保我们是在原地修改权重张量的值，而不是创建一个新的张量
  • 这种写法保持了原始张量的身份和内存位置
  1. -=

  • 这是减法和赋值复合运算符 ，等价于：

    python 复制代码 
    conv2d.weight.data = conv2d.weight.data - (lr * conv2d.weight.grad)

  • 但使用-=更高效，因为它进行原地操作

  1. lr
  • 学习率（learning rate），这里为0.03
  • 控制每次参数更新的步长大小
  • 是梯度下降算法中的超参数
  1. conv2d.weight.grad
  • 这是权重参数的梯度（偏导数）
  • 在调用l.sum().backward()后，PyTorch会自动计算并存储这个梯度
  • 梯度表示损失函数相对于该参数的变化率（即"最陡上升方向"）

整体含义

这行代码执行了梯度下降更新规则：

新权重 = 旧权重 - 学习率 × 梯度

用数学公式表示：
Wnew=Wold−η⋅∂L∂WW_{\text{new}} = W_{\text{old}} - \eta \cdot \frac{\partial L}{\partial W}Wnew=Wold−η⋅∂W∂L

其中：

  • WWW 是权重参数
  • η\etaη 是学习率（lr）
  • ∂L∂W\frac{\partial L}{\partial W}∂W∂L 是损失函数对权重的梯度（conv2d.weight.grad）

为什么需要这样写？

  1. 手动优化 ：这里没有使用PyTorch内置的优化器（如torch.optim.SGD），而是手动实现更新规则

  2. 原地操作 ：使用[:]和-=确保在原地修改权重值，保持张量的身份

  3. 分离计算图 ：通过操作.data，我们避免了创建新的计算图节点，这对于这种简单的手动更新是合适的

对比标准做法

在更复杂的网络中，通常使用优化器：

python 复制代码 
# 标准做法（不是这里的代码）
optimizer = torch.optim.SGD(conv2d.parameters(), lr=lr)
optimizer.zero_grad()
l.sum().backward()
optimizer.step()  # 自动执行所有参数的更新

而这里的代码相当于手动实现了optimizer.step()的功能，但只针对这一个特定的权重参数。

总结

这行代码是神经网络训练的核心：根据损失函数的梯度方向，以学习率控制的步长，更新模型参数，使损失函数值减小。这是深度学习模型能够从数据中学习的基本机制。

5. 互相关和卷积

核心内容整理

  1. 运算上的区别

    • 互相关运算：是卷积神经网络中实际执行的操作。如图6.2.1所示，它直接将卷积核在输入上滑动并计算元素乘机和。
    • 严格卷积运算 ：为了得到严格的数学卷积输出，需要先将卷积核在水平和垂直方向上进行翻转，然后再执行与互相关相同的滑动乘加操作。

  2. 为何在深度学习中效果等价

    • 图片中的关键论点是：因为卷积核的权重是从数据中学习得到的，而不是人为预先设定的固定值。
    • 假设一个网络通过互相关运算学习到了一个最优的卷积核 K。
    • 如果这个网络改而执行严格的卷积运算，它最终会学习到另一个卷积核 K' 。这个 K' 将会是 K 经过水平和垂直翻转后的结果。
    • 因此，无论是用 K 执行互相关运算，还是用翻转后的 K' 执行严格的卷积运算，最终的输出结果是完全相同的。学习过程会自动补偿这两种运算方式之间的差异。

  3. 术语上的约定俗成

    • 尽管存在上述技术区别，但为了与绝大多数深度学习文献和框架（如PyTorch、TensorFlow）的标准术语保持一致 ，人们普遍将层中执行的"互相关运算"直接称为卷积运算。
    • 同样，我们也习惯地将卷积核张量中的可学习参数称为权重（weights）。

总结说明

虽然数学定义上"互相关"与"卷积"不同 （差一个翻转核的步骤），但在卷积神经网络（CNN）的实践应用中，二者可以视为等价的。其根本原因在于卷积核的可学习性使得网络能够自适应地调整参数，从而使得两种运算方式所能达到的最终效果完全一致。

因此，在深度学习领域，"卷积层"实际上执行的是"互相关"操作，这是一种普遍且被接受的术语简化。

6. 特征映射和感受野

  1. 特征映射（Feature Map）

卷积层的输出被称为"特征映射"。这是因为：

  • 它是一个映射：它将输入数据（如图像）从一个空间维度转换到了另一个（可能不同的）空间维度。
  • 它包含特征 ：输出值（如图6.2.1中的19, 25, 37, 43）不是简单的像素值，而是输入中某种特定特征（如边缘、角点、纹理）的强度响应 。卷积核（如[[0,1],[2,3]]）可以看作是一个特征检测器。

因此，特征映射 可以理解为一张"图"，这张图标识了原始输入中哪些位置存在由卷积核所定义的特定特征。

  1. 感受野（Receptive Field）

这是理解卷积神经网络层次结构最重要的概念之一。

  • 定义 ：对于网络中任意一个元素（例如特征映射中的一个值），它的感受野指的是所有可能影响其计算结果的输入层元素（像素）所覆盖的区域。
  • 示例解析 ：
    • 第一层感受野 ：在图6.2.1中，输出值19是由输入中一个2x2的区域（[[0,1],[3,4]]）与卷积核计算得出的。因此，值19的感受野就是输入上的这个2x2区域。
    • 深层感受野 ：图片接着假设我们将这个2x2的输出（Y）作为第二个卷积层 的输入。如果第二个卷积层使用一个2x2的卷积核，那么它的输出可能只是一个值z。这个值z是由第一层的输出Y（4个值）计算得来的，而Y的每个值又是由输入的一个2x2区域计算得来的。因此，输出值z的感受野覆盖了最初输入中一个更大的区域（所有9个元素）。
  1. 构建更深网络的意义

最后一个核心结论：通过构建更深的网络（堆叠更多的卷积层），我们可以使深层特征图中的元素拥有更大的感受野。

  • 浅层网络：只能捕捉局部的、细节的特征（如小边缘、小色块）。
  • 深层网络 ：深层中的神经元能够看到输入图像中更大范围的区域，从而能够整合底层信息，检测更复杂、更全局的模式，如物体的部件（眼睛、鼻子）甚至整个物体。

这种感受野随网络深度增加而指数级增大的特性，是卷积神经网络能够有效处理图像理解任务（如分类、检测、分割）的根本原因之一。它使得网络能够从局部到全局、从细节到整体地理解一幅图像。

7. 小结

  • 二维卷积层的核心计算是二维互相关运算。最简单的形式是，对二维输入数据和卷积核执行互相关操作，然后添加一个偏置。

  • 我们可以设计一个卷积核来检测图像的边缘。

  • 我们可以从数据中学习卷积核的参数。

  • 学习卷积核时，无论用严格卷积运算或互相关运算，卷积层的输出不会受太大影响。

  • 当需要检测输入特征中更广区域时，我们可以构建一个更深的卷积网络。

8. 练习

1. 构建一个具有对角线边缘的图像X。

  • 1. 如果将本节中举例的卷积核K应用于X，会发生什么情况?
    • 卷积核K（例如边缘检测核如Sobel或Prewitt）会对图像X中的对角线边缘产生响应。输出会突出显示这些边缘的位置，但具体效果取决于核的方向是否与边缘方向匹配。如果核是水平或垂直方向的，可能无法有效检测对角线边缘。
  • 2. 如果转置X会发生什么?
    • 转置X（行列互换）会改变边缘的方向。例如，原对焦线边缘可能变为相反方向。应用卷积核K后，输出会相应改变，因为核现在处理的是转置后的图像结构。
  • 3. 如果转置K会发生什么?
    • 转置K（核矩阵的行列互换）会改变核检测的方向。例如，水平边缘核转置后可能变为垂直边缘核。应用于X时，输出会对应核的新方向，可能无法有效捕获原对角线边缘。

2. 在我们创建的Conv2D自动求导时，有什么错误消息?

  • 错误消息通常涉及输入数据维度不匹配、核大小或步长设置不当、或通道数不一致。例如："Input and kernel dimensions not compatible" 或 "Stride too large for input size"。

3. 如何通过改变输入张量和卷积核张量，将互相关运算表示为矩阵乘法?

  • 可以通过im2col操作将输入图像块展开为矩阵的列，同时将卷积核展平为行向量。互相关运算即可表示为这两个矩阵的乘法，输出结果可重排为特征图形式。

4. 手工设计一些卷积核。

  • 1. 二阶导数的核的形式是什么?
    • 拉普拉斯核示例：[0101−41010]\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} 0101−41010 ，用于检测边缘。
  • 2. 积分的核的形式是什么?
    • 积分核通常为全1矩阵，例如19[111111111]\frac{1}{9}\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}91 111111111 （均值滤波），实现局部求和。
  • 3. 得到d次导数的最小核的大小是多少?
    • 最小核大小为d+1d+1d+1（如一阶导数最小核大小2，二阶导数最小核大小3）。
相关推荐
技术闲聊DD2 小时前
深度学习（1）-利用Pytorch2结合U-Net大模型实现图像降噪
pytorch·深度学习·手写体识别·u-net模型
ACEEE12225 小时前
解读DeepSeek-V3.2-Exp：基于MLA架构的Lightning Index如何重塑长上下文效率
人工智能·深度学习·算法·架构·deep
学技术的大胜嗷7 小时前
使用BatchNorm偏置填充边界：确保推理一致性与数值稳定性
人工智能·深度学习·图像生成
雲_kumo9 小时前
深度学习入门：从神经网络基础到模型训练优化
人工智能·深度学习·神经网络
东方芷兰9 小时前
LLM 笔记 —— 02 大语言模型能力评定
人工智能·笔记·python·神经网络·语言模型·自然语言处理·cnn
羞儿9 小时前
【pytorch】数据增强与时俱进，未来的改进和功能将仅添加到 torchvision.transforms.v2 转换中
pytorch·python·深度学习·数据增强
森诺Alyson10 小时前
前沿技术借鉴研讨-2025.9.23 （数据不平衡）
论文阅读·人工智能·经验分享·深度学习·论文笔记
jackylzh13 小时前
深度学习中， WIN32为 Windows API 标识，匹配 Windows 系统，含 32/64 位
人工智能·python·深度学习
一条星星鱼17 小时前
深度学习是如何收敛的？梯度下降算法原理详解
人工智能·深度学习·算法
热门推荐
01HarmonyOS NEXT开发进阶（十四）：HarmonyOS应用开发者基础认证试题集汇总及答案解析02KGG转MP3工具|非KGM文件|解密音频03UV安装并设置国内源04jdk21下载、安装（Windows、Linux、macOS）05GitHub 镜像站点0646个Nano-banana 精选提示词，持续更新中07Linux下V2Ray安装配置指南08MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法09零基础搭建赛博朋克个人主页：蓝耘Claude Code完整实战教程10最新b站加密关键字段的逆向（视频和评论爬取）