背包问题概述
背包问题 (Knapsack problem) 是⼀种组合优化的 NP完全问题。
问题可以描述为:给定⼀组物品,每种物品都有⾃⼰的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最⾼。
根据物品的个数,分为如下⼏类:
• 01 背包问题:每个物品只有⼀个
• 完全背包问题:每个物品有⽆限多个
• 多重背包问题:每件物品最多有 si 个
• 混合背包问题:每个物品会有上⾯三种情况......
•分组背包问题:物品有 n 组,每组物品⾥有若⼲个,每组⾥最多选⼀个物品
其中上述分类⾥⾯,根据背包是否装满,⼜分为两类:
• 不⼀定装满背包
• 背包⼀定装满
优化⽅案:
• 空间优化 - 滚动数组(重点掌握)
• 单调队列优化
• 贪⼼优化
根据限定条件的个数,⼜分为两类:
• 限定条件只有⼀个:⽐如体积 -> 普通的背包问题
• 限定条件有两个:⽐如体积 + 重量 -> ⼆维费⽤背包问题
根据不同的问法,⼜分为很多类:
• 输出⽅案
• 求⽅案总数
• 最优⽅案
• ⽅案可⾏性
其实还有很多分类,但是我们仅需了解即可。
因此,背包问题种类⾮常繁多,题型⾮常丰富,难度也是⾮常难以捉摸。但是,尽管种类⾮常多,都是从 01 背包问题演化过来的。所以,⼀定要把 01 背包问题学好。
No.1 01背包【模板】


第一问:

第二问:

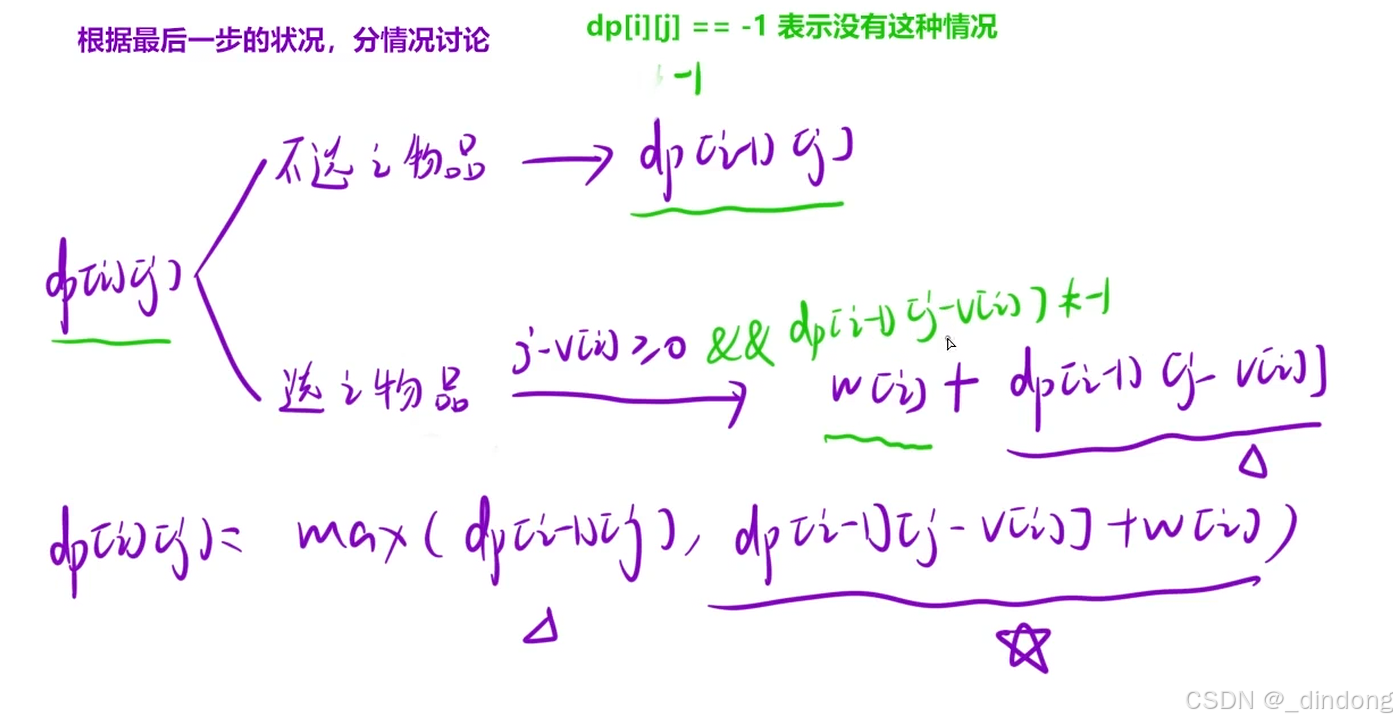
初始化
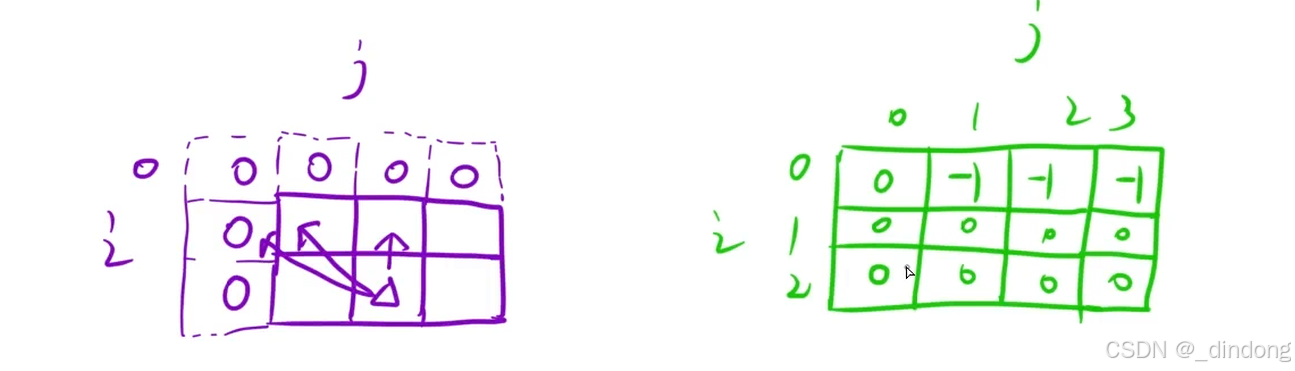
cpp
#include <iostream>
#include<string.h>
using namespace std;
const int N =1010;
int n,V,v[N],w[N],dp[N][N];
int main() {
cin>>n>>V;
for(int i=1;i<=n;++i)cin>>v[i]>>w[i];
//第一问
for(int i=1;i<=n;++i)
{
for(int j=1;j<=V;++j)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i])dp[i][j]=max(dp[i][j],w[i]+dp[i-1][j-v[i]]);
}
}
cout<<dp[n][V]<<endl;
//清空输出->初始化
memset(dp,0,sizeof dp);
for(int j=1;j<=V;++j)dp[0][j]=-1;
//第二问
for(int i=1;i<=n;++i)
{
for(int j=1;j<=V;++j)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i]&&dp[i-1][j-v[i]]!=-1)dp[i][j]=max(dp[i][j],w[i]+dp[i-1][j-v[i]]);
}
}
cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
return 0;
}滚动数组空间优化:
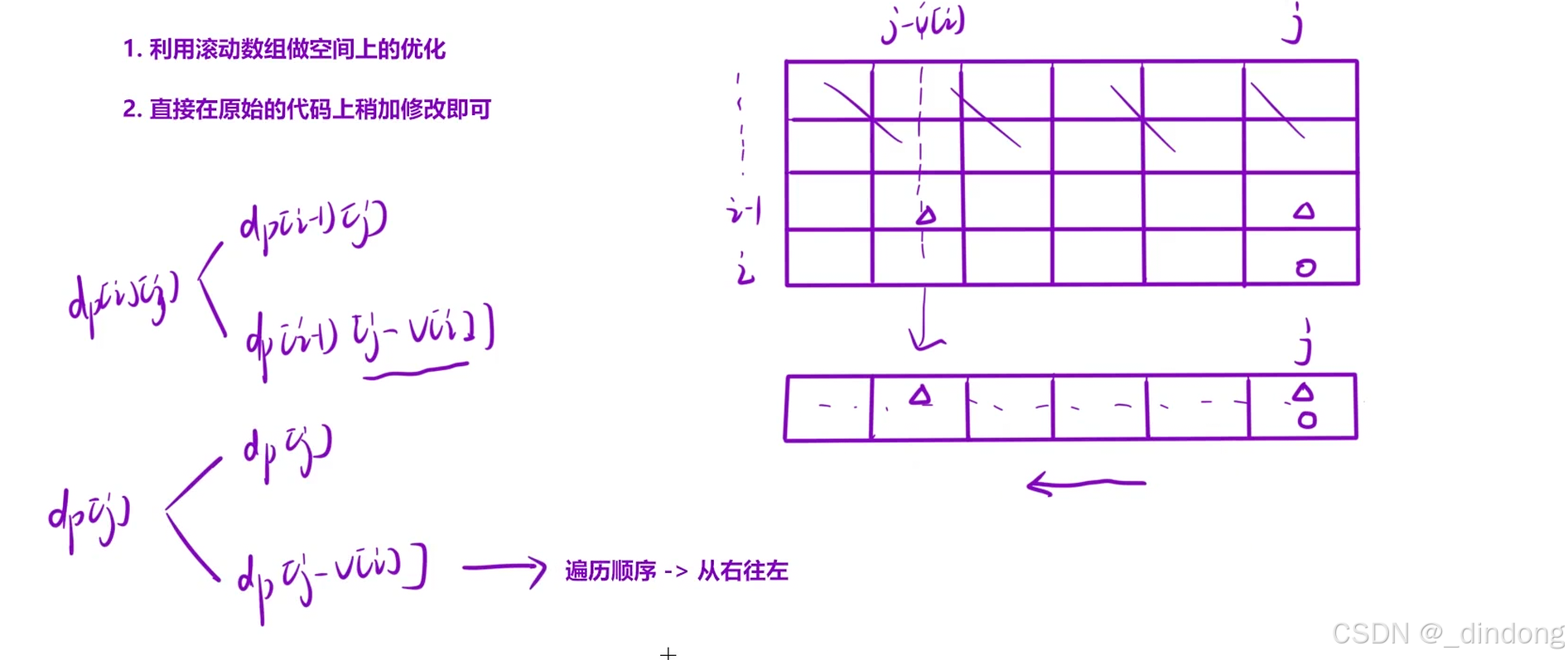
cpp
#include <iostream>
#include<string.h>
using namespace std;
const int N =1010;
int n,V,v[N],w[N],dp[N];
int main() {
cin>>n>>V;
for(int i=1;i<=n;++i)cin>>v[i]>>w[i];
//第一问
for(int i=1;i<=n;++i)
{
for(int j=V;j>=v[i];--j) //修改遍历顺序
{
dp[j]=max(dp[j],w[i]+dp[j-v[i]]);
}
}
cout<<dp[V]<<endl;
//清空输出->初始化
memset(dp,0,sizeof dp);
for(int j=1;j<=V;++j)dp[j]=-1;
//第二问
for(int i=1;i<=n;++i)
{
for(int j=V;j>=v[i];--j) //修改遍历顺序
{
if(dp[j-v[i]]!=-1)dp[j]=max(dp[j],w[i]+dp[j-v[i]]);
}
}
cout<<(dp[V]==-1?0:dp[V])<<endl;
return 0;
}No.2 分割等和子集

转化成,在数组中选择一些数出来,让这些数的和等于sum/2。
相当于01背包只有体积一个限定条件

cpp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size(),sum=0;
for(auto&x:nums)sum+=x;
if(sum%2)return false;
int aim=sum/2;
vector<vector<bool>> dp(n+1,vector<bool>(aim+1));
//第一列表示sum=0,全为true
for(int i=1;i<=n;++i)dp[i][0]=true;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=aim;++j)
{
dp[i][j]=dp[i-1][j];
if(j>=nums[i-1])dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];
}
}
return dp[n][aim];
}
};滚动数组空间优化:
cpp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size(),sum=0;
for(auto&x:nums)sum+=x;
if(sum%2)return false;
int aim=sum/2;
vector<bool> dp(aim+1);
dp[0]=true;
for(int i=1;i<=n;++i)
{
for(int j=aim;j>=nums[i-1];--j)
{
dp[j]=dp[j]||dp[j-nums[i-1]];
}
}
return dp[aim];
}
};No.3 目标和
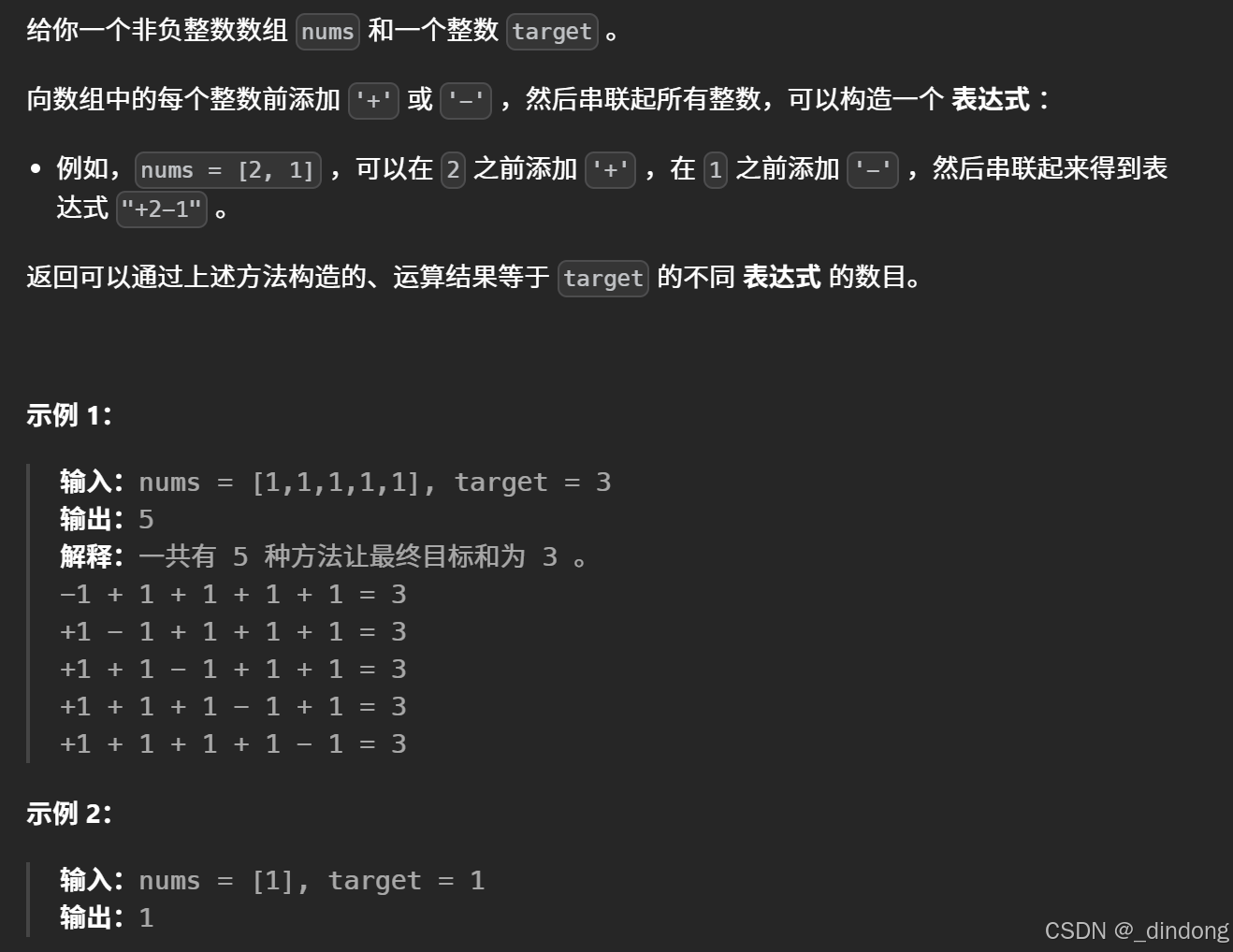

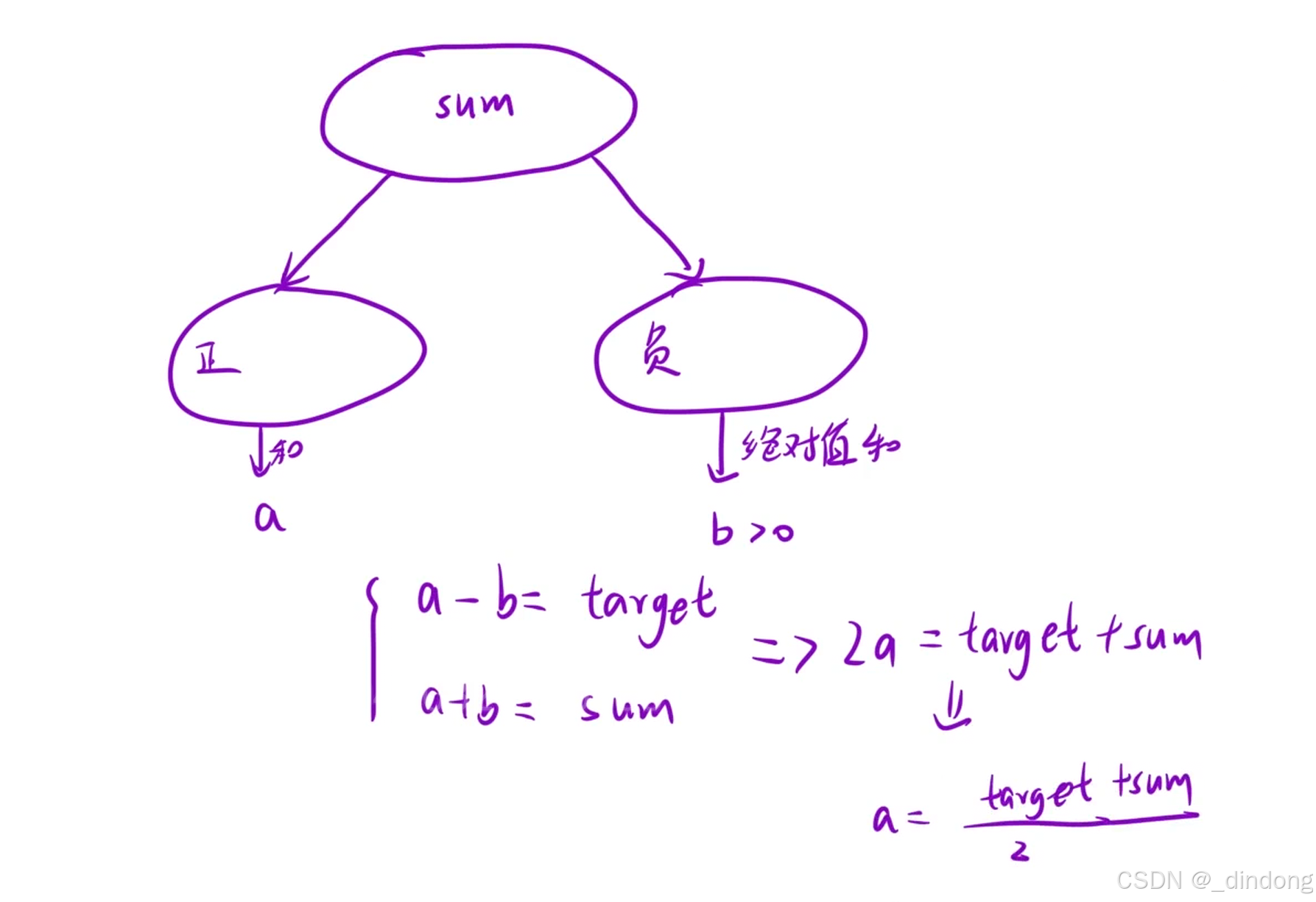
那么就变得和上一题一样了

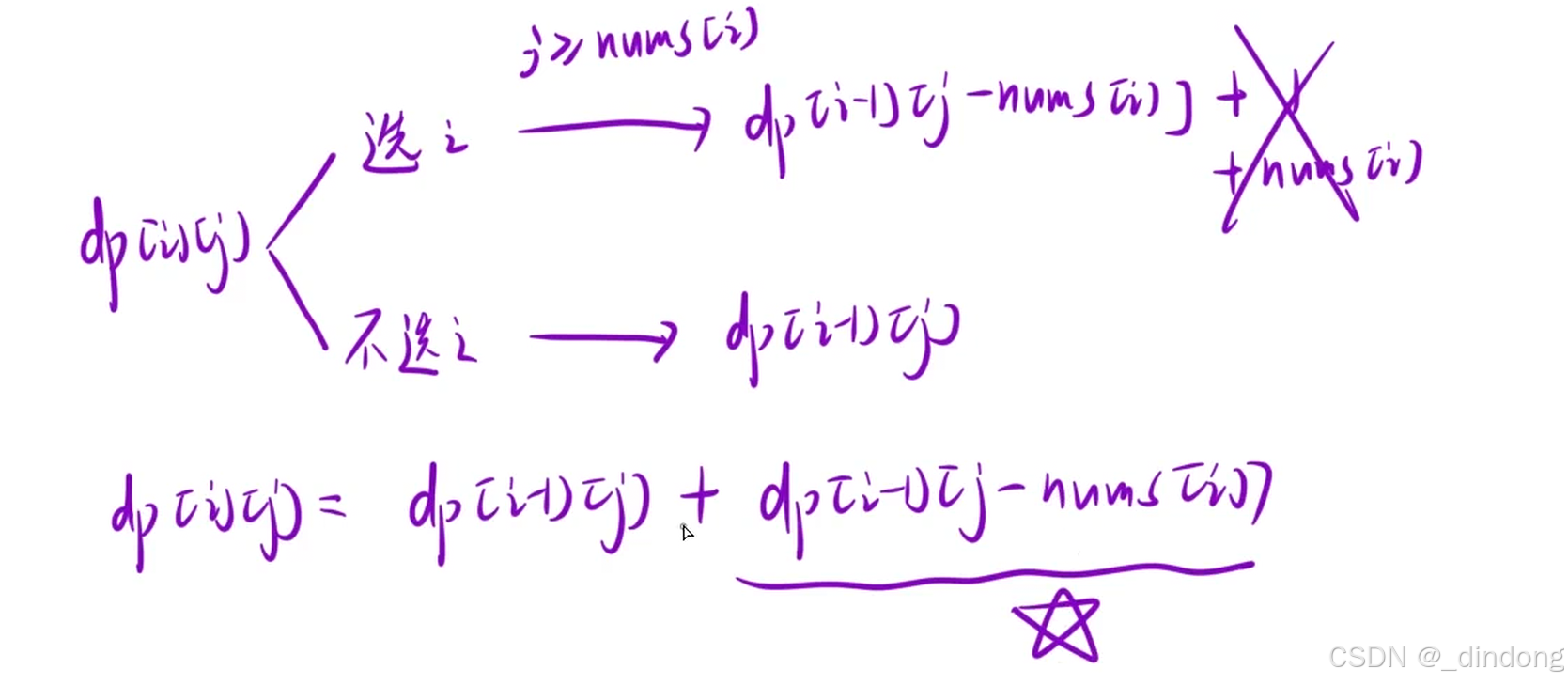
初始化
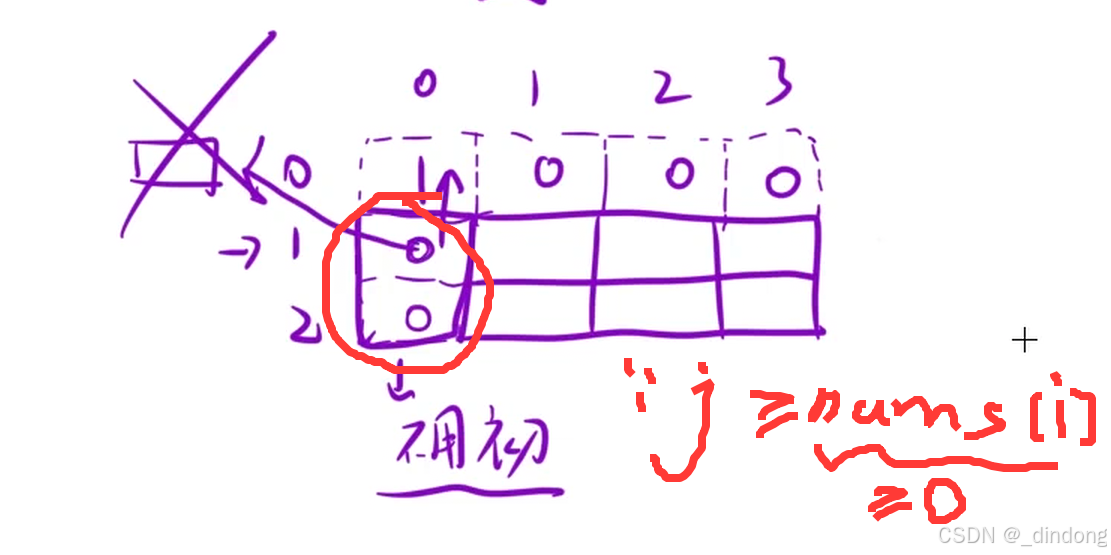
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(auto&x:nums)sum+=x;
int aim=(sum+target)/2;
if(aim<0||(sum+target)%2)return 0;
int n=nums.size();
vector<vector<int>> dp(n+1,vector<int>(aim+1));
dp[0][0]=1;
for(int i=1;i<=n;++i)
{
//第一列的初始化在填表过程中完成
for(int j=0;j<=aim;++j)
{
dp[i][j]=dp[i-1][j];
//注意下标映射!!!!
if(j>=nums[i-1])dp[i][j]+=dp[i-1][j-nums[i-1]];
}
}
return dp[n][aim];
}
};滚动数组空间优化:
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum=0;
for(auto&x:nums)sum+=x;
int aim=(sum+target)/2;
if(aim<0||(sum+target)%2)return 0;
int n=nums.size();
vector<int> dp(aim+1);
dp[0]=1;
for(int i=1;i<=n;++i)
{
//第一列的初始化在填表过程中完成
for(int j=aim;j>=nums[i-1];--j)
{
//注意下标映射!!!!
dp[j]+=dp[j-nums[i-1]];
}
}
return dp[aim];
}
};No.4 最后一块石头的重量II
1049. 最后一块石头的重量 II - 力扣(LeetCode)


思考一下可以转换成目标和问题
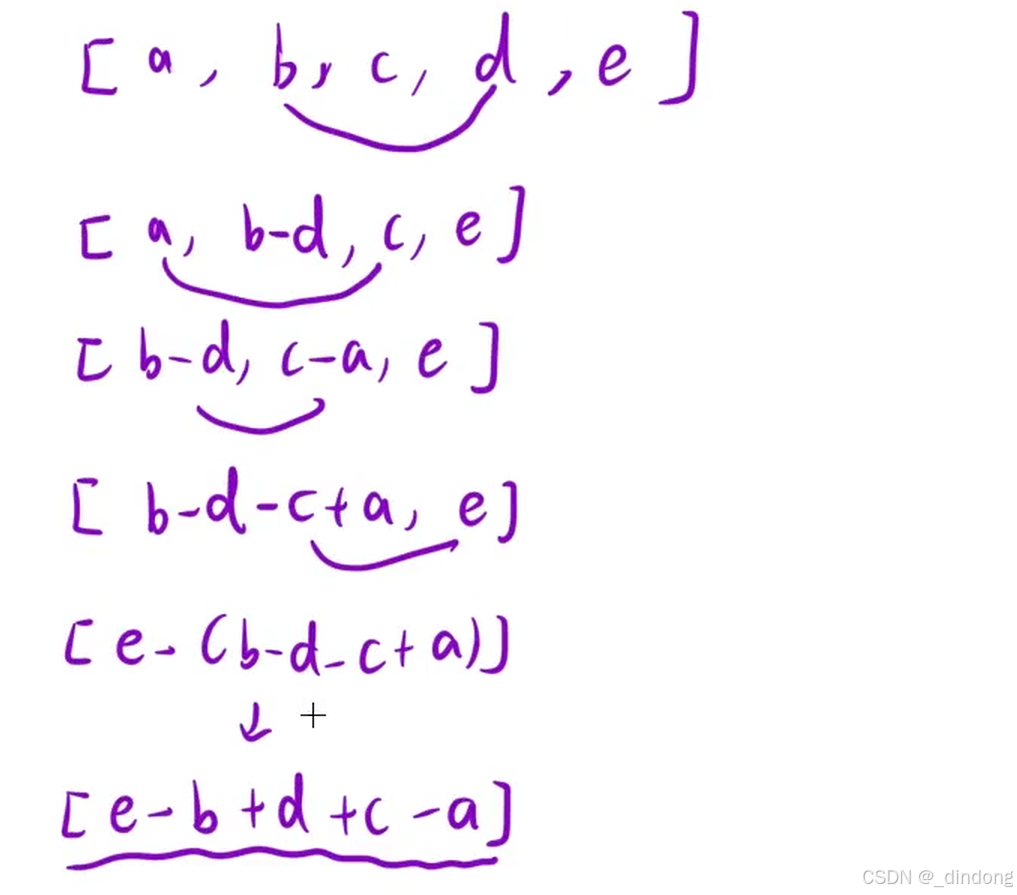
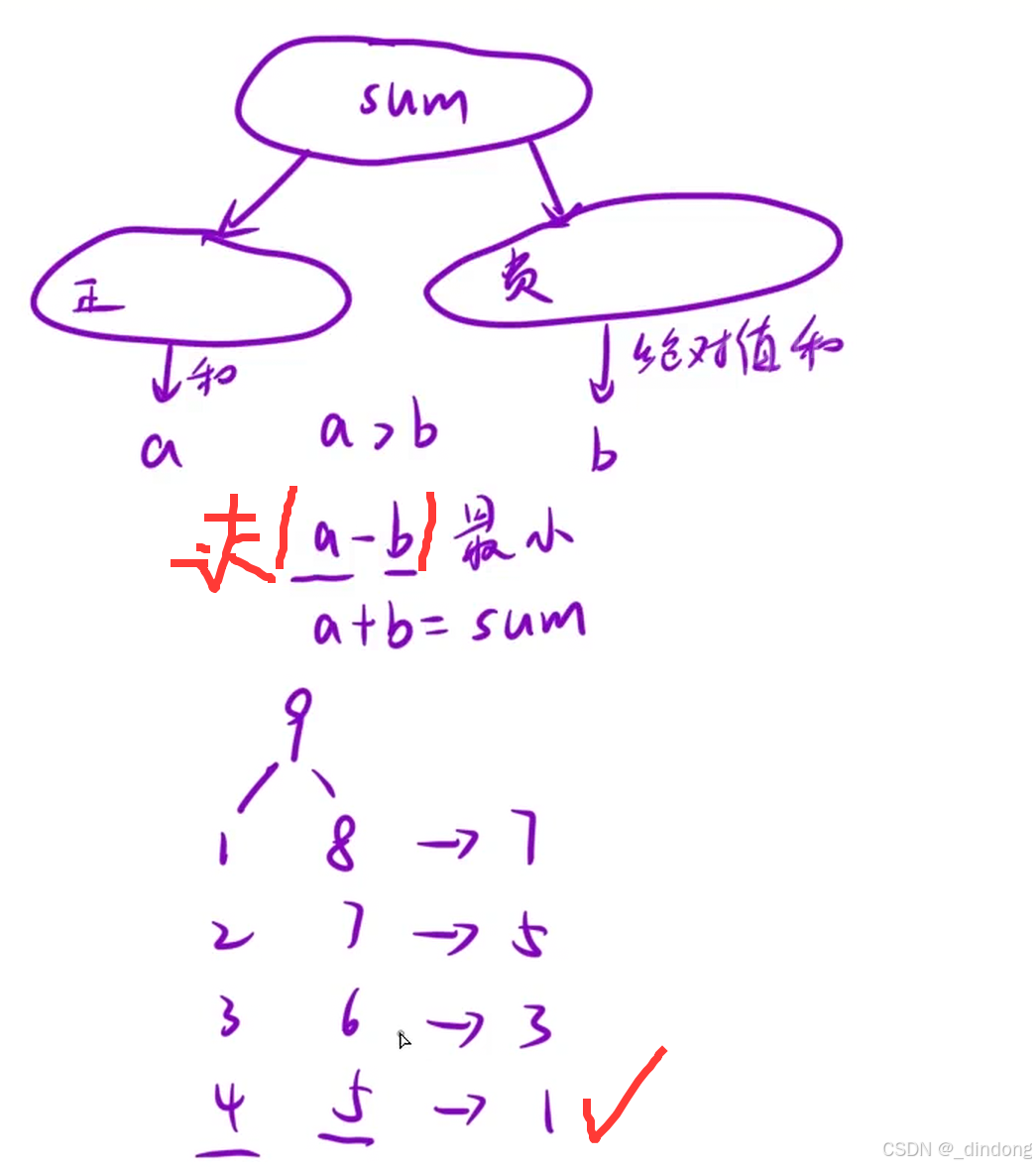



数组空,j值为0的时候都是零
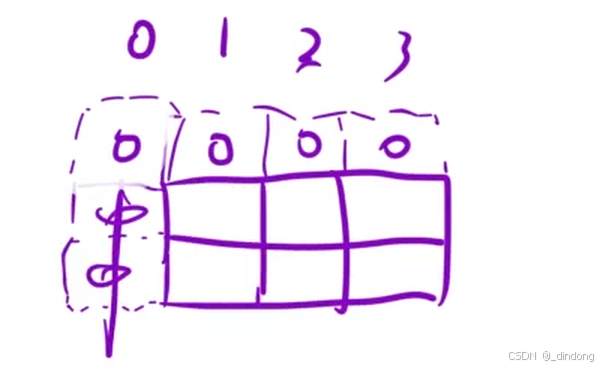
cpp
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sum=0;
for(auto&x:stones)sum+=x;
int aim=sum/2,n=stones.size();
vector<vector<int>> dp(n+1,vector<int>(aim+1));
for(int i=1;i<=n;++i)
{
for(int j=1;j<=aim;++j)
{
dp[i][j]=dp[i-1][j];
//注意下标映射!!!
if(j>=stones[i-1])dp[i][j]=max(dp[i][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
}
}
return sum-dp[n][aim]*2;
}
};滚动数组空间优化:
cpp
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sum=0;
for(auto&x:stones)sum+=x;
int aim=sum/2,n=stones.size();
vector<int> dp(aim+1);
for(int i=1;i<=n;++i)
{
for(int j=aim;j>=stones[i-1];--j)
{
//注意下标映射!!!
dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);
}
}
return sum-dp[aim]*2;
}
};No.5 将一个数字表示成幂的和的方案数
2787. 将一个数字表示成幂的和的方案数 - 力扣(LeetCode)


由于数据可能非常大,应该采用范围更大的类型存储数据,但double float都不允许取模操作,所以我们创建long long.
cpp
class Solution {
const int N=1e9+7;
public:
int numberOfWays(int n, int x) {
//dp[i][j]表示从0~i选择数的x次方,恰好等于j的,方案总数
vector<vector<long long>> dp(n+1,vector<long long>(n+1));
//i是0,j全部无效;j是0,都只有一种方法(i=0)
for(int i=0;i<=n;++i)dp[i][0]=1;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
dp[i][j]=dp[i-1][j];
long long p=pow(i,x);
if(j>=p)dp[i][j]+=dp[i-1][j-p];
dp[i][j]%=N;
}
}
return dp[n][n];
}
};滚动数组空间优化:
cpp
class Solution {
const int N=1e9+7;
public:
int numberOfWays(int n, int x) {
//dp[i][j]表示从0~i选择数的x次方,恰好等于j的,方案总数
vector<long long> dp(n+1);
//i是0,j全部无效;j是0,都只有一种方法(i=0)
dp[0]=1;
for(int i=1;i<=n;++i)
{
long long p=pow(i,x);
for(int j=n;j>=p;--j)
{
dp[j]+=dp[j-p];
dp[j]%=N;
}
}
return dp[n];
}
};