目录
[1. 任务安排问题](#1. 任务安排问题)
[1353. 最多可以参加的会议数目](#1353. 最多可以参加的会议数目)
[1235. 规划兼职工作](#1235. 规划兼职工作)
[1488. 避免洪水泛滥](#1488. 避免洪水泛滥)
[2. 数组区间变换问题](#2. 数组区间变换问题)
[3362. 零数组变换 III 最大堆 + 差分](#3362. 零数组变换 III 最大堆 + 差分)
[3480. 删除一个冲突对后最大子数组数目 最小与次小](#3480. 删除一个冲突对后最大子数组数目 最小与次小)
[3. 数学推式子](#3. 数学推式子)
[3154. 到达第 K 级台阶的方案数](#3154. 到达第 K 级台阶的方案数)
[3495. 使数组元素都变为零的最少操作次数 [ l, r ] 先求 [ 1, n ]](#3495. 使数组元素都变为零的最少操作次数 [ l, r ] 先求 [ 1, n ])
[2929. 给小朋友们分糖果 II 排列组合 + 容斥原理](#2929. 给小朋友们分糖果 II 排列组合 + 容斥原理)
1. 任务安排问题
按开始 / 结束时间排序，堆 or 二分 找上一个。
1353. 最多可以参加的会议数目
给二元组 每个会议的 [开始，结束] 时间 （每个会议可以在这个区间的任意一天参加）最多可以参加的会议数。
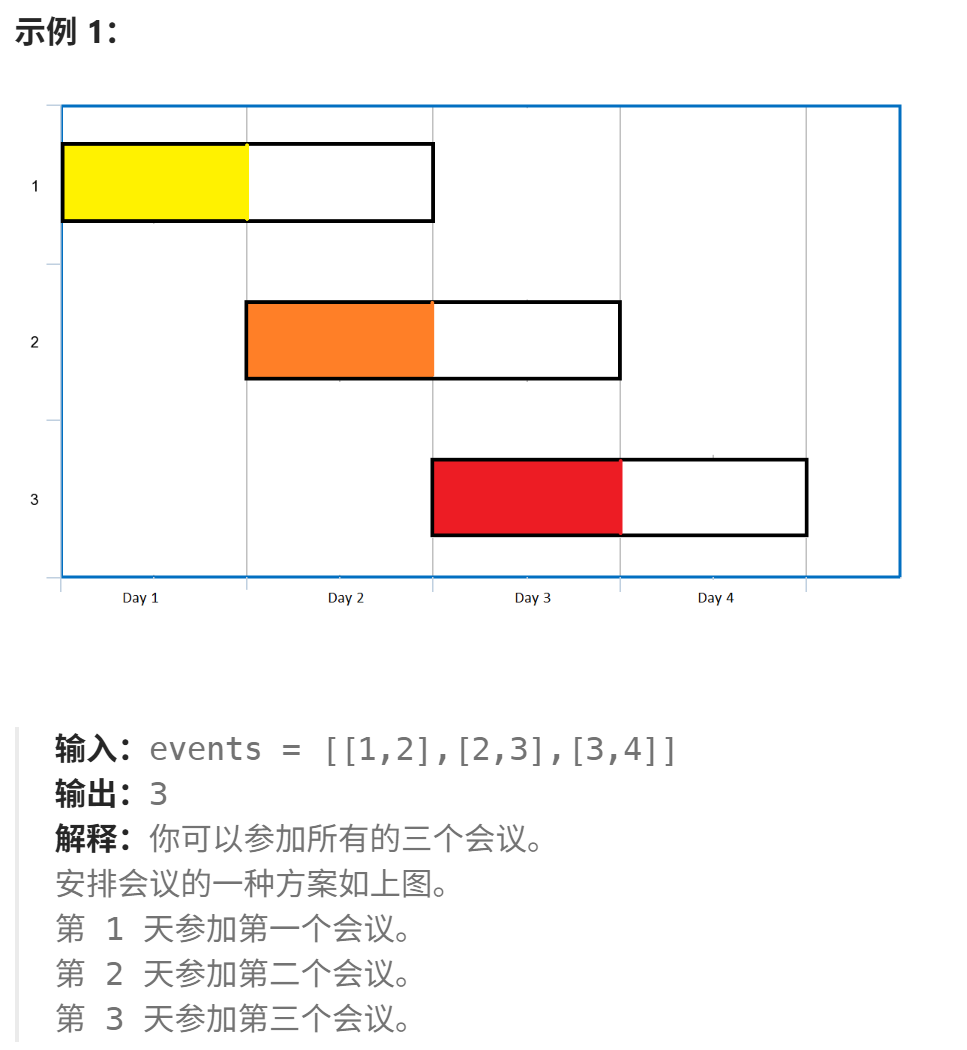
我们从前到后 遍历每一天 看每天该排哪个会议 。 能参加需要开始时间早于这天。
在此基础，（贪心）我们要选能参加的会议中 最早结束的那个。
于是对于 按开始时间排序的这些会议，对每一天 做三个步骤：
加入日程：如果开始时间早于现在，就添加到 todo中；
踢出过期：结束时间晚于现在的，删掉。
选择最早结束：在加入日程时 记录结束时间的最小堆；
python
import heapq
class Solution:
def maxEvents(self, events: List[List[int]]) -> int:
events.sort()
n,maxn,ans,j=len(events),max(e[1] for e in events),0,0
todo=[]
for i in range(1,maxn+1):
# 加入可以参加的会议
while j<n and events[j][0]<=i:
heappush(todo,events[j][1])
j+=1
# 删除过期会议
while todo and cando[0]<i:
heappop(todo)
# 安排最早结束的会议
if todo:
heappop(todo)
ans+=1
return ans法二：并查集
按照结束时间排序，先安排结束的早的 。安排在能安排的最早的一天。
安排就向后串联，指向后一天（用并查集实现）
python
class Solution:
def maxEvents(self, events: List[List[int]]) -> int:
events.sort(key=lambda e: e[1])
mx = events[-1][1]
fa = list(range(mx + 2))
def find(x: int) -> int:
if fa[x] != x:
fa[x] = find(fa[x])
return fa[x]
ans = 0
for start_day, end_day in events:
x = find(start_day) # 查找从 start_day 开始的第一个可用天
if x <= end_day:
ans += 1
fa[x] = x + 1 # 标记 x 已占用
return ans1235. 规划兼职工作
给定任务的**[开始时间，结束时间，收益]** 问不重合任务的最大收益。
dp[i] 代表做到前 i 个工作的最大收益（单调增的）。
上一个能衔接 的任务 根据结束时间。所以按结束时间排序。
状态转移 如果做这个任务 就衔接 a[i][0] 前，最后一个 即结束时间最晚的（二分找）
python
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
n=len(endTime)
a=sorted(zip(startTime,endTime,profit),key=lambda p:p[1])
dp=[0]*(n+1)
for i in range(n):
k=bisect_right(a,a[i][0],hi=i,key=lambda p:p[1])
dp[i+1]=max(dp[i],dp[k]+a[i][2])
return dp[n]1488. 避免洪水泛滥
输入下雨情况，输出抽水安排。
rains 代表下雨情况，0代表不下（可以抽水），其余代表哪个位置下。
需要安排抽水，使得区域在下一次下雨前被抽过水。
先用 full 存满的 { 湖：日期 }，dry存可以抽水的日期（有序集合SortedList 方便后续二分找）。
发现当前湖要爆了，在存的日期之后 ，找最早的可以抽水的时间。（时间晚的灵活度更高 可以抽其他湖）
解释 ：越晚的抽水日，灵活性越大，可以用于更晚装满的湖。所以越晚的抽水日 越应该留到后面再使用。
python
class Solution:
def avoidFlood(self, rains: List[int]) -> List[int]:
n = len(rains)
ans = [-1] * n
full_day = {} # lake -> 装满日
dry_day = SortedList() # 未被使用的抽水日
for i, lake in enumerate(rains):
if lake == 0:
ans[i] = 1 # 先随便选一个湖抽干
dry_day.add(i) # 保存抽水日
continue
if lake in full_day:
j = full_day[lake]
# 必须在 j 之后，i 之前把 lake 抽干
# 选一个最早的未被使用的抽水日，如果选晚的，可能会导致其他湖没有可用的抽水日
k = dry_day.bisect_right(j)
if k == len(dry_day):
return [] # 无法阻止洪水
d = dry_day[k]
ans[d] = lake
dry_day.discard(d) # 移除已使用的抽水日
full_day[lake] = i # 插入或更新装满日
return ans2. 数组区间变换问题
3362. 零数组变换 III 最大堆 + 差分
q [l,r] 可以把这个区间的数都 -1，最终要把初始数组nums变成 ≤0 。问最多可以删多少 q。
从前往后过 nums，如果这个位置 nums[i] > 0 我们就需要选 i 之前的 ，结束位置尽量靠后的 q 。
（ i 之前 为了能删这个位置，结束位置贪心 越往后影响位置越多）
根据开始时间排序 ；结束时间尽量靠后：把结束时间塞入最大堆（负数最小堆）
区间加减：差分 diff。 需要选用这个 q，把当前 sum +=1，把结束位置后一位 diff -1。
python
class Solution:
def maxRemoval(self, nums: List[int], queries: List[List[int]]) -> int:
queries.sort(key=lambda q: q[0]) # 按照左端点从小到大排序
h = []
diff = [0] * (len(nums) + 1)
sum_d = j = 0
for i, x in enumerate(nums):
sum_d += diff[i]
# 维护左端点 <= i 的区间
while j < len(queries) and queries[j][0] <= i:
heappush(h, -queries[j][1]) # 取相反数表示最大堆
j += 1
# 选择右端点最大的区间
while sum_d < x and h and -h[0] >= i:
sum_d += 1
diff[-heappop(h) + 1] -= 1
if sum_d < x:
return -1
return len(h)3480. 删除一个冲突对后最大子数组数目 最小与次小
有1~n的数，给定一些冲突对（可以删除其中的一个 ）求最多的 不包含冲突对的子数组数目。
若没有删除机制，在 i 位置能达到的子数组：要在所有冲突对 a≥i 中最小的 b 前面。
讨论不同的 i ：倒着往前推 如果这个位置有 冲突对的 a，更新 min b。从 i 开始就有 min b - i个。
倒着讨论 ，a 用来判断现在是否需要考虑 这个冲突对，b -> 最小和次小 用来看当前 i 最往后到哪个。
每次删最小的 b0，变成次小的 b1 ，多出来的答案extra += b1-b0
要看删哪个 q 累积的 extra 最多，有新的最小的 b0 就把 extra = 0 统计新的 q 。
python
class Solution:
def maxSubarrays(self, n: int, conflictingPairs: List[List[int]]) -> int:
groups = [[] for _ in range(n + 1)]
for a, b in conflictingPairs:
if a > b:
a, b = b, a
groups[a].append(b)
ans = max_extra = extra = 0
b0 = b1 = n + 1
for i in range(n, 0, -1):
pre_b0 = b0
# 最小和次小
for b in groups[i]:
if b < b0:
b0, b1 = b, b0
elif b < b1:
b1 = b
ans += b0 - i # 不考虑删除的统计
if b0 != pre_b0: # 重新统计连续相同 b0 的 extra
extra = 0
extra += b1 - b0
max_extra = max(max_extra, extra)
return ans + max_extra3. 数学推式子
3154. 到达第 K 级台阶的方案数
从1->k的方案数，可以向上跳2的幂次，也可以向下一级（但不能连续）
排列组合
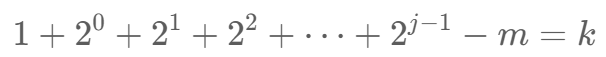把向上向下 分别拿出来 再插空。
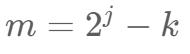
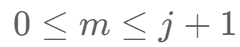在 j+1 中 插空m C ( j+1,m )
python
class Solution:
def waysToReachStair(self, k: int) -> int:
ans = 0
for j in range(30):
m = (1 << j) - k
if 0 <= m <= j + 1:
ans += comb(j + 1, m)
return ans记忆化搜索
（现在位置，之前jump次数，上一次是不是向下跳）
入口（1, 0, False） 如果超过 k+1 之后下不去了，就是0。
分向上 or 向下 两种跳跃方案统计。
python
class Solution:
def waysToReachStair(self, k: int) -> int:
@cache # 缓存装饰器，避免重复计算 dfs 的结果（记忆化）
def dfs(i: int, j: int, pre_down: bool) -> int:
if i > k + 1: # 无法到达终点 k
return 0
res = 1 if i == k else 0
res += dfs(i + (1 << j), j + 1, False) # 操作二
if not pre_down:
res += dfs(i - 1, j, True) # 操作一
return res
return dfs(1, 0, False)3495. 使数组元素都变为零的最少操作次数 [ l, r ] 先求 [ 1, n ]
对每个询问 q = [ l, r ] 选两个数变成 除以4 向下取整，都变成0 需要多少次。
设 f(n) 为 [ 1, n ] 需要除以4的次数 ，则 [ l, r ] 的次数为 f(r) - f(l-1)， （区间问题 转化为1开始）
选两个数操作 因为是连续的区间 不存在一个数超大的情况 可以两两消去 ，答案为 f(r) - f(l-1) 除以2 向上取整。
每个数需要除以4的次数 -> 4进制的位数。
设 m 为 n 的二进制位数，k为 ≤ m 的最大偶数。
2^k ~ n 的（n-2^k+1）个数 都要 k//2 +1 次 。
k之前的即为：1~3 1次； 4~15 2次 以此类推
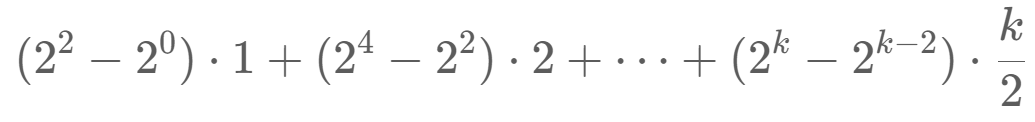
化简为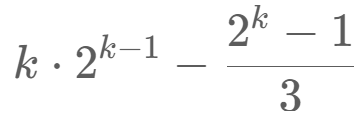 
后面减了一个4的等比数列
最终 f(n) 为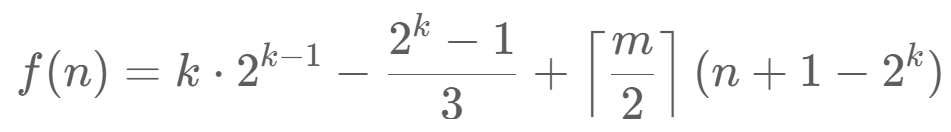 
python
def f(n: int) -> int:
if n == 0:
return 0
m = n.bit_length()
k = (m - 1) // 2 * 2
res = (k << k >> 1) - (1 << k) // 3
# 前面 2^(k-1) 为了防止 k=0, 先左移k次 再右移1次
# 由于 4的幂次%3=1 后面的-1 可以省略
return res + (m + 1) // 2 * (n + 1 - (1 << k))
class Solution:
def minOperations(self, queries: List[List[int]]) -> int:
return sum((f(r) - f(l - 1) + 1) // 2 for l, r in queries)2929. 给小朋友们分糖果 II 排列组合 + 容斥原理
将 n 颗糖果分给 3 位小朋友，确保没有任何小朋友得到超过 limit 颗糖果，总方案数 。
无条件分，隔板法 C(n+2,2) ；减去不符合条件的。
容斥原理 超过 limit：至少一人超过 - 至少两人超过 + 至少三人超过
至少一人：先拿出来 limit +1 ，剩下再分。
python
def c2(n: int) -> int:
return n * (n - 1) // 2 if n > 1 else 0
class Solution:
def distributeCandies(self, n: int, limit: int) -> int:
return c2(n + 2) - 3 * c2(n - limit + 1) + 3 * c2(n - 2 * limit) - c2(n - 3 * limit - 1)