标题:<Plug-and-Play PDE Optimization for 3D Gaussian Splatting: Toward High-Quality Rendering and Reconstruction>
来源:匿名作者
文章目录
- 一、摘要
- 二、准备知识
- 三、主要方法
-
- [3.1 基于PDE的3DGS优化](#3.1 基于PDE的3DGS优化)
- [3.2 基于MPM的解决方案](#3.2 基于MPM的解决方案)
- [3.3 粒子约束](#3.3 粒子约束)
- 实验
一、摘要
3DGS通过3DGS基元表征场景,实现了高质量新型视图合成与快速渲染速度,彻底革新了辐射场重建技术。然而在处理复杂场景时,由于redundant 和ambiguous geometric structures(冗余模糊几何结构),该方法会出现画面模糊blurring 和漂浮floaters 。我们发现这一现象源于高斯函数优化过程中的不稳定性。针对这一局限,我们 提出了一种基于偏微分方程的即插即用优化方法 ,有效突破了传统3DGS方法在新型视图合成、表面重建等任务中的优化限制。首先,我们从理论上推导出3DGS优化流程可建模为偏微分方程,并引入粘性项(viscous term ,PDE中用于确保优化过程稳定的阻尼项) 确保优化过程稳定。其次,采用材料点法(MPM)获得偏微分方程的稳定数值 解,同时强化全局与局部约束条件。此外,我们还创新性地提出高斯函数密集化策略和粒子约束机制,确保细节呈现的精细度。大量定性与定量实验表明,本方法在渲染与重建质量上达到了业界领先水平。
二、准备知识
3DGS: 每个GS基元由可学习的中心位置 μ μ μ、不透明度 o o o、颜色 c c c 和协方差矩阵𝚺参数化:
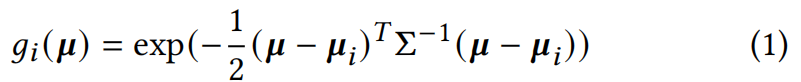
3DGS被投影到图像平面上,通过 α α α混合技术结合将 N N N个有序高斯排序来计算像素颜色 C C C:
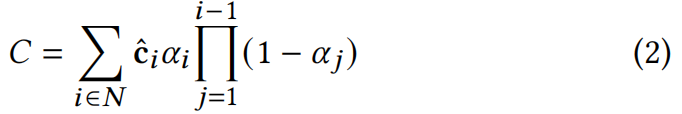
材料点法(MPM) 是一种用于求解偏微分方程的离散方法,广泛应用于固体与流体模拟领域。该方法融合了系统的双重视角 :在拉格朗日描述 中,系统被视作由众多具有独立属性的粒子构成的离散相;而欧拉描述则将系统视为连续相,从而实现对粒子运动的整体性描述。
具体来说,粒子的运动方程随时间 t t t演化如下: f ( v , x ) = ∂ v / ∂ t f(v,x)=\partial v/\partial t f(v,x)=∂v/∂t。然后,使用MPM将该函数离散化为: f ( v , x ) = v t + 1 − v t f(v,x)=v^{t+1}−v^t f(v,x)=vt+1−vt。
梯度分析
3DGS采用梯度下降法进行场景优化,这一过程对于实现高质量的场景表示至关重要。每个高斯𝑔𝑖都关联一组可训练的属性 Γ𝑡𝑖={𝝁𝑖,c𝑖,𝑜𝑖,s𝑖,q𝑖},在优化过程中,每个属性的更新由以下公式给出:
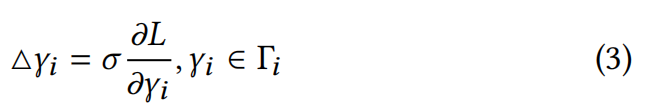
损失的梯度可以通过链式法则计算:
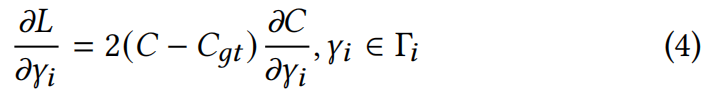
通过沿与像素 u u u 相关的视线射线 l l l 积分,并考虑 N N N个有序高斯,该方程可以展开为:
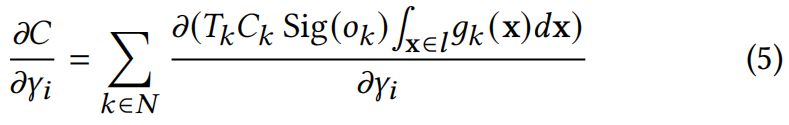
如附录A.1所示,当高斯的尺度较小时,位置梯度的magnitude明显大于其他参数梯度(∼表示渐近等价, 𝑟 q , i 𝑟_{q,i} rq,i表示四元数定义的 q i q_i qi的更新方向):
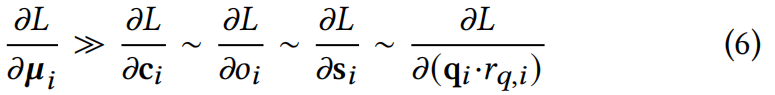
三、主要方法
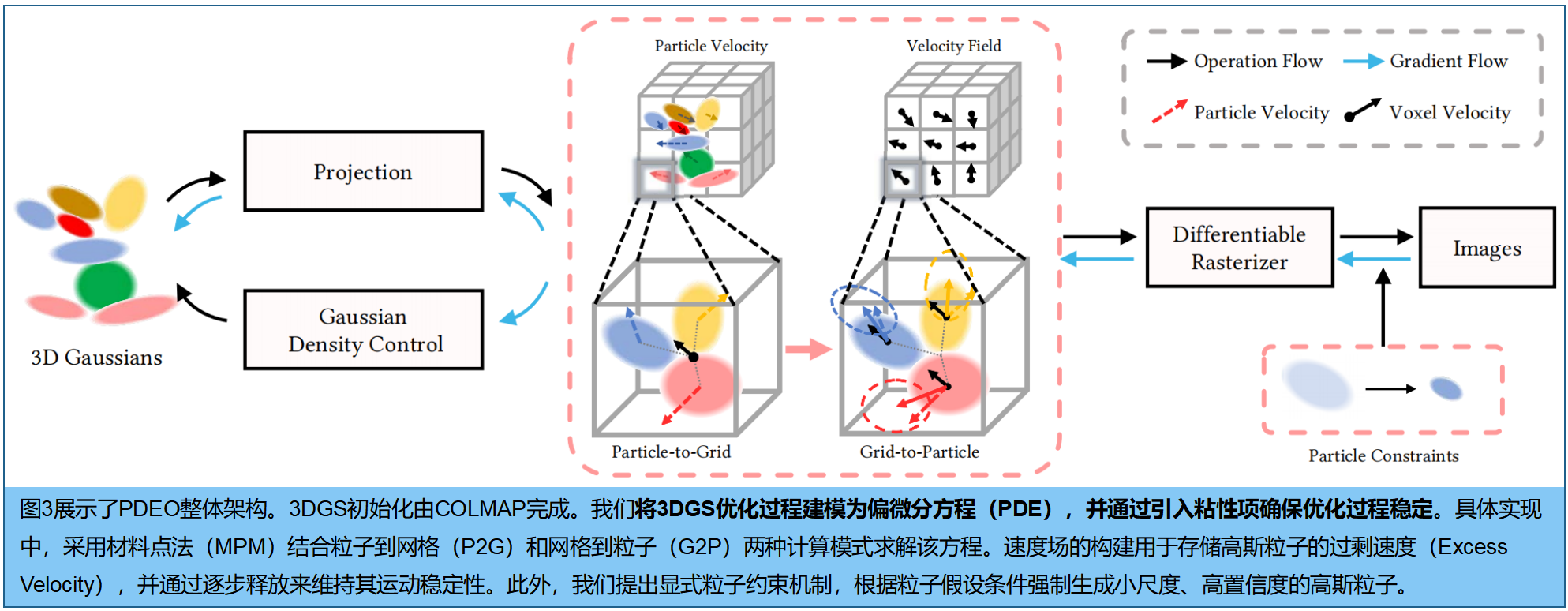
3.1 基于PDE的3DGS优化
公式化。在偏微分方程中,时间代表属性序列的更新过程,通过改变属性使系统状态向下一状态过渡,类似于3DGS的迭代步骤。因此,更新过程中高斯函数的属性是时间 t t t的函数。对于原始3DGS,优化过程可表示为: μ i t + 1 = μ i t + σ ∂ L t ∂ μ i t μ^{t+1}_i=μ^{t}_i+\sigma\frac {\partial L^t}{\partial μ^t_i} μit+1=μit+σ∂μit∂Lt 其中 σ \sigma σ为学习率, μ i t μ^{t}_i μit是高斯 g i g_i gi在时间 t t t的位置。
高斯 i i i在时间 t t t的离散速度定义 为 v i t = μ i t + 1 − μ i t v_i^t=μ_i^{t+1}-μ_i^t vit=μit+1−μit ,因此,连续形式的速度方程为:

计算方程在时间 t t t的偏导数( d d t \frac {d}{d_t} dtd是全导数,因为 μ , c , o , s , q μ ,c ,o ,s ,q μ,c,o,s,q 都随时间变化):
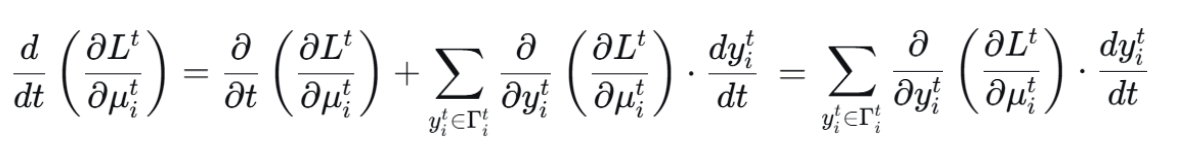
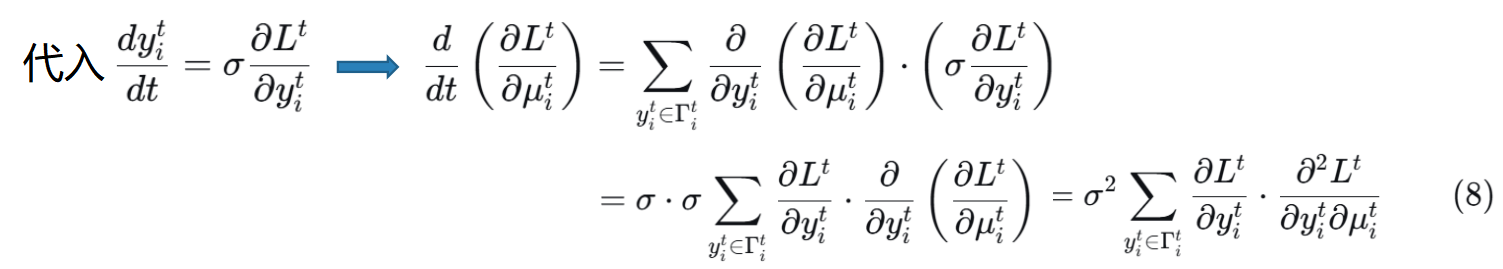
物质导数(Material Derivative):也称为随体导数,是流体力学中的一个核心概念。它描述的是跟随一个流体微元(或一个粒子)运动时,其某个物理量(如速度、温度等)随时间的变化率:

根据时间导数的定义和牛顿-莱布尼茨公式,最终的运动方程被定义为:
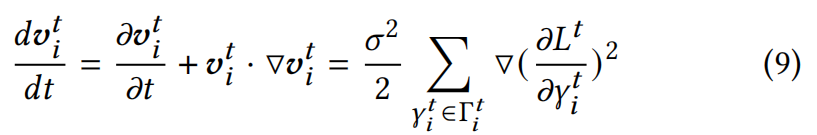
粘性项 Viscous Term 。与3DGS优化不同,在流体模拟过程中,粒子位置更新是稳定且可控的,这归因于运动方程中的粘性项。
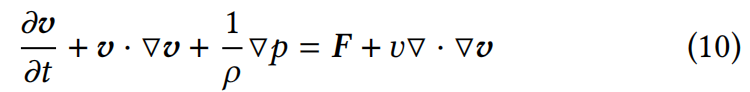
其中 ▽ v = 0 \bigtriangledown v=0 ▽v=0, t t t为时间, ρ ρ ρ是密度, p p p是压力, u u u是粘度, F F F是重力加速度, v v v是流体场的速度,等于粒子位置 μ μ μ的导数,即 v = ∂ μ ∂ t v=\frac {\partial μ}{\partial t} v=∂t∂μ。粘性项 u ▽ ⋅ ▽ v u \bigtriangledown·\bigtriangledown v u▽⋅▽v本质上为系统中的粒子赋予了加速度,使其趋向于周围环境的平均速度。这种作用可等效理解为将粒子的速度与周围粒子的平均速度进行混合。
受流体仿真的启发,在3DGS优化过程中引入粘性项,即将方程9改写为:
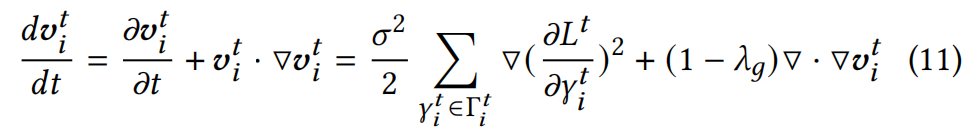
其中 λ g λ_g λg是权重系数。遵循偏微分方程的基本原理,当 L L L等于零时, v v v的能量会随着 t t t逐渐减少,最终趋近于零。因此,引入粘性并不会改变方程的解,因为 t t t趋于无穷大(3DGS的理论结果)。
为此,离散解的计算方式如下( N i N_i Ni是高斯 g i g_i gi的近邻集合):
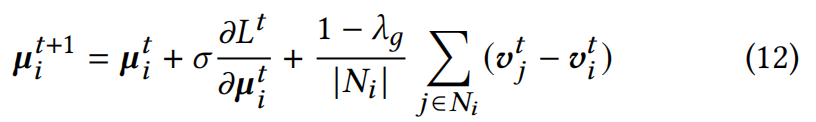
3.2 基于MPM的解决方案
公式12的离散形式可近似为:
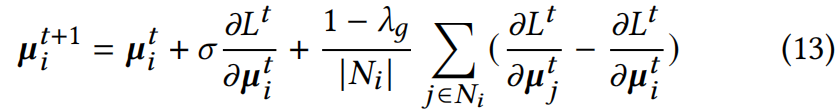
由于计算相邻3DGS粒子运动的成本过高,采用粒子网格方法(MPM) 将3DGS视为粒子进行求解。具体的,在3DGS优化过程中融合了 Particle-to-Grid (P2G) 和Grid-to-Particle (G2P)两种策略 ,来抑制粒子运动,同时提供额外的运动引导来解运动方程。 我们通过将场景空间划分为体素网格来构建速度场。粒子可以通过在体素网格中存储过剩速度并从体素网格获取额外速度来更新运动状态。因此,粒子实际上通过局部速度场信息进行调控,从而将粘性项引入优化过程。
Particle-to-Grid P2G过程构建了一个 grid,用于存储粒子在体素网格中的过剩速度 (Excess Velocity,流体中的粒子相对于其周围局部流体的速度)。如前所述,高斯 g i g_i gi的位置通过 △ μ i t = ∂ L t ∂ μ i t \bigtriangleup μ_i^t=\frac {\partial L^t}{\partial μ_i^t} △μit=∂μit∂Lt 进行更新,该值由损失函数梯度计算得出。小尺度高斯分布更容易发生位置突变,这会导致优化过程不稳定。因此,适度降低速度将有助于优化效果。具体而言,我们采用P2G过程来衰减粒子速度 △ μ i t \bigtriangleup μ_i^t △μit,同时保留粒子的运动特性 。我们在step t t t将粒子 g i g_i gi的过剩速度存储到体素网格 V n V_n Vn 中。
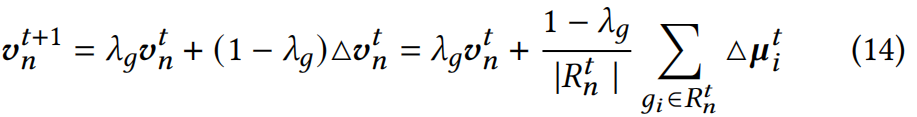
其中 R n t R_n^t Rnt属于 R t = R_t= Rt={ R 0 t , . . . . , R 𝑁 t R^t_0,....,R^t_𝑁 R0t,....,RNt}是体素网格 V n V_n Vn内包含的粒子集合, v n t v_n^t vnt是存储在 V n V_n Vn中的体素速度, λ g λ_g λg是权重系数。我们在附录A.2中展示了 λ g λ_g λg的选择对总梯度没有影响
Grid-to-Particle grid 不仅抑制粒子速度,还为粒子提供额外的运动引导。由于速度场代表了粒子在体素网格中的平均运动趋势,因此体素速度随后被用来引导粒子的运动
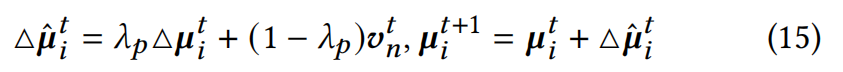
其中粒子速度被系数 λ g λ_g λg抑制,而 △ μ ^ i t \bigtriangleup \hat{μ}_i^t △μ^it 则是更新后的速度。更新后的速度代表了粒子位置优化的最可能方向。不同粒子的速度相互作用,从而抵消了不同方向上位置属性的突变,同时还能从体素速度中获得额外的速度指引。因此,位置梯度的变化成功被粘性项所引导。
3.3 粒子约束
尺度损失 在 PDE 中,粒子具有无尺度特性。然而,大尺度高斯会占据较大空间,这与偏微分方程系统的假设条件相矛盾。为此,我们为3DGS引入尺度约束:
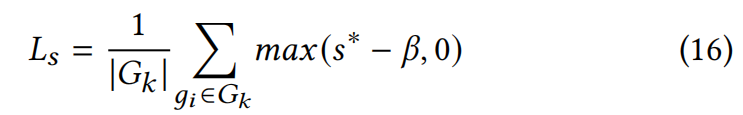
𝑠 ∗ 𝑠^∗ s∗表示 g i g_i gi的最大尺度, G k G_k Gk是视点 k k k中可见的3DGS的集合, β β β是尺度的边界。这种损失函数惩罚了大尺度的3DGS。小尺度的3DGS确保了捕捉高频细节的能力。
置信度损失 由于3DGS被描述为偏微分方程中的粒子,因此需要避免使用半透明的高斯,确保GS具有高置信度并满足粒子假设:
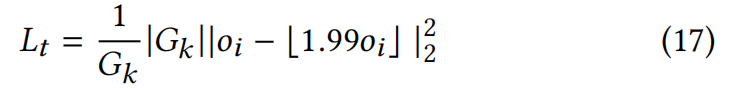
高斯稠密化 稠密化在 3DGS 中被用于克隆和分割新高斯体以填补空隙,(通过计算视空间位置的位移梯度平均值来判断是否稠密化)。本文通过速度场引导克隆分裂过程。具体的,计算粒子速度场与体素速度场之间的余弦相似度 ,当满足 c o s ( △ μ i , u n ) > θ p cos(\bigtriangleup μ_i,u_n)>θ_p cos(△μi,un)>θp 时,将高斯 g i g_i gi稠密化。
实验
数据集 。新视角合成 选取了17个场景:Mip-nerf360的6个场景、《坦克与神庙》的7个场景,以及ScanNet++的4个场景。在表面重建 方面,在丹麦技术大学提供的15个场景和《坦克与神庙》的7个场景上进行测试。场景包含有界室内环境和无界室外环境,。
实现细节。偏微分方程优化算法(PDEO)可轻松集成到现有基于 3DGS 的方法中,例如MipGS和2DGS,用于新型视图合成和表面重建任务。为确保评估一致性,我们采用原方法的默认参数设置:𝜆𝑔= 0.8、𝜆𝑝= 0.8、𝜓= 0.2、𝜃𝑝=120◦、𝛽= 0.6、𝜔𝑡= 0.04、𝜔𝑠= 0.04,并通过迭代逐步将𝜏从1递增至2.5。所有实验均在单个V100 GPU上完成。
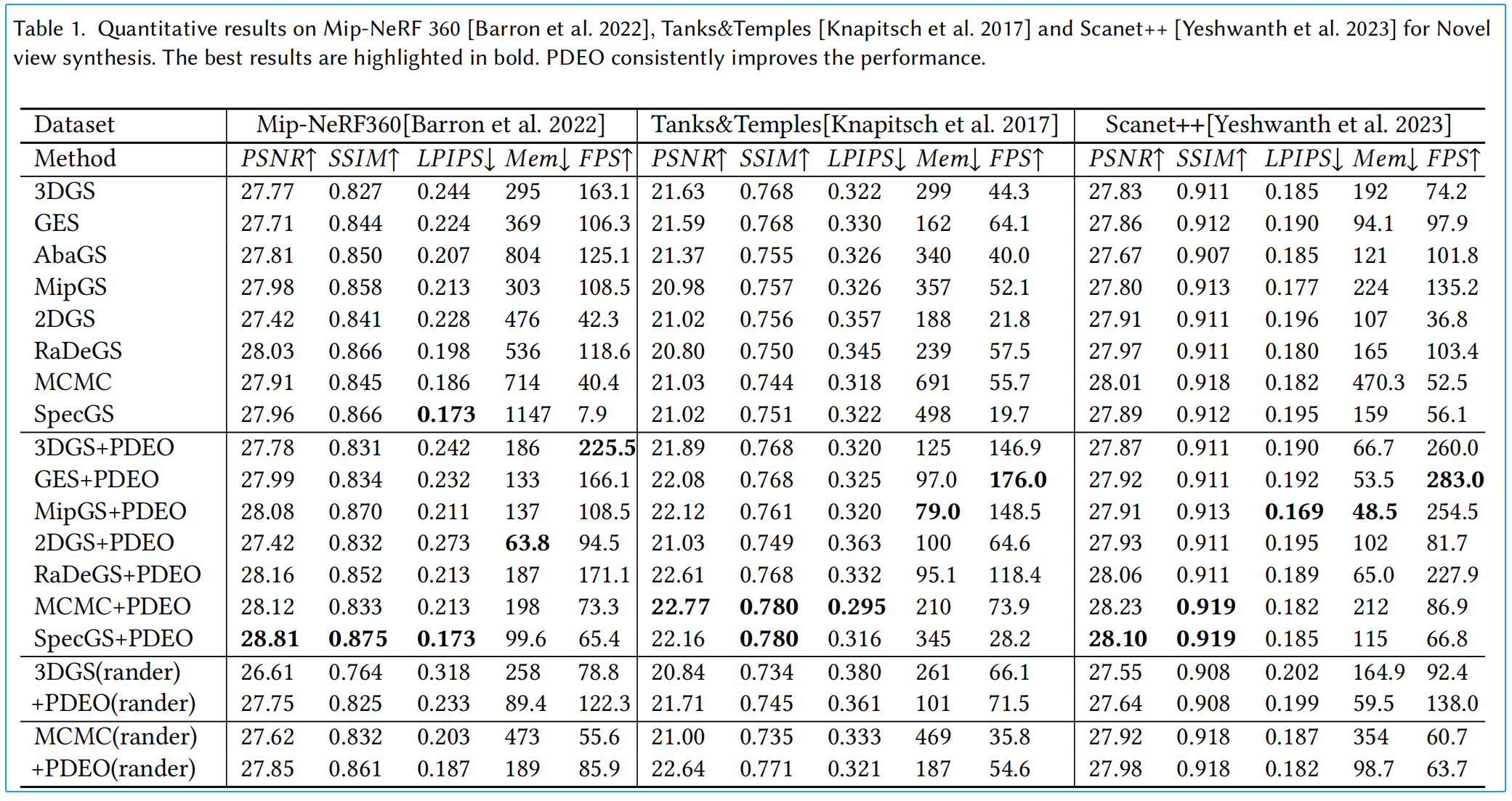
新视角合成
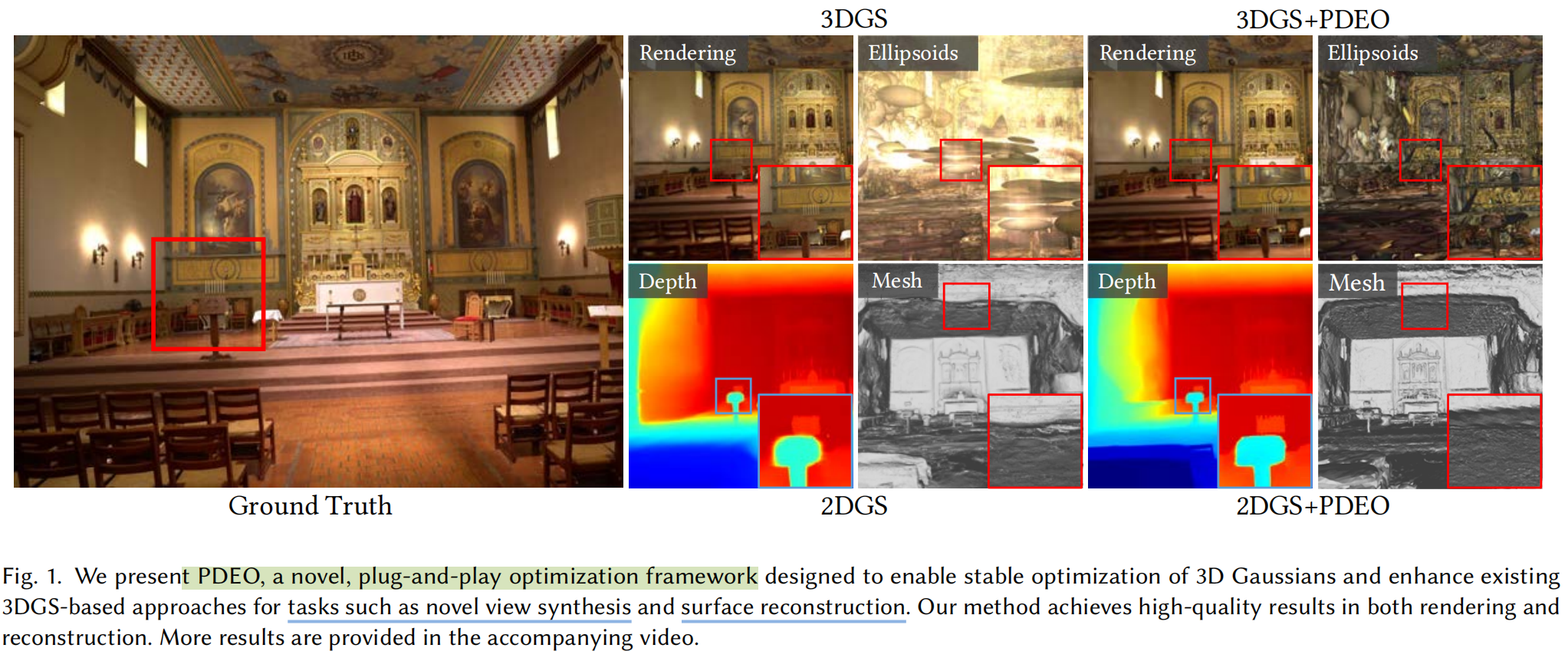
本研究PDEO方法不仅大幅提升了基于3DGS算法的性能,同时显著优化了内存使用效率,见下表和下图。


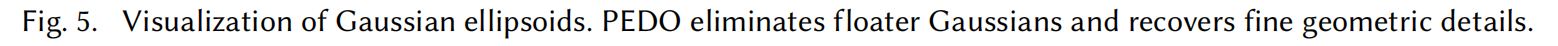
表面重建
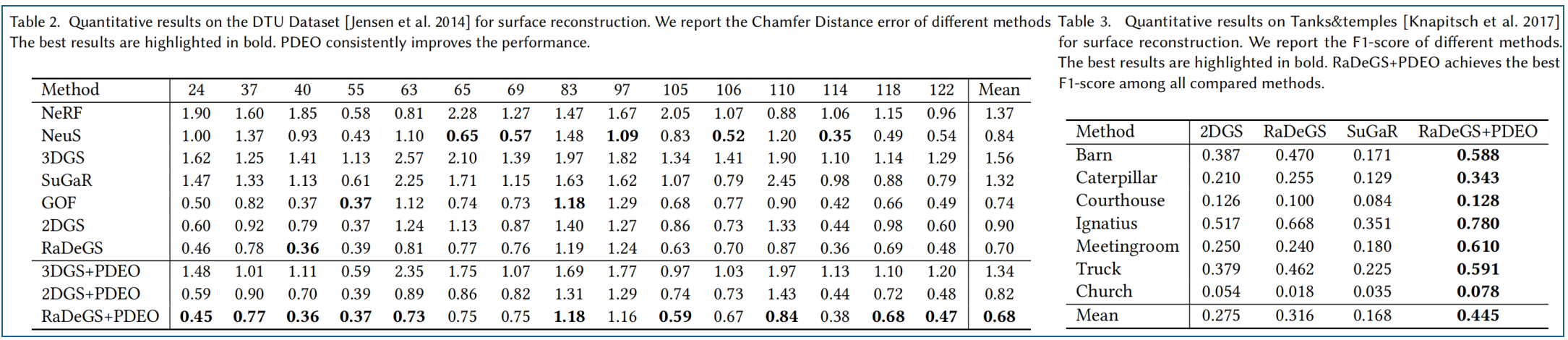
PDEO与基于最新的3DGS几何重建技术的方法相结合,分别与2DGS、RaDeGS以及SuGaR 对比。如表2和表3所示,在DTU数据集上,PDEO在CD误差指标上持续优于基于3D几何重建的方法;在Tanks & Temples数据集上则在F1分数指标上表现更优。如图6所示,RaDeGS+PDEO在重建质量上展现出更优的几何精度和平滑度,其重建效果在定性评估中更为出色。这表明PDEO不仅能有效去除漂浮物,还能精准保留几何细节,从而显著提升重建质量。

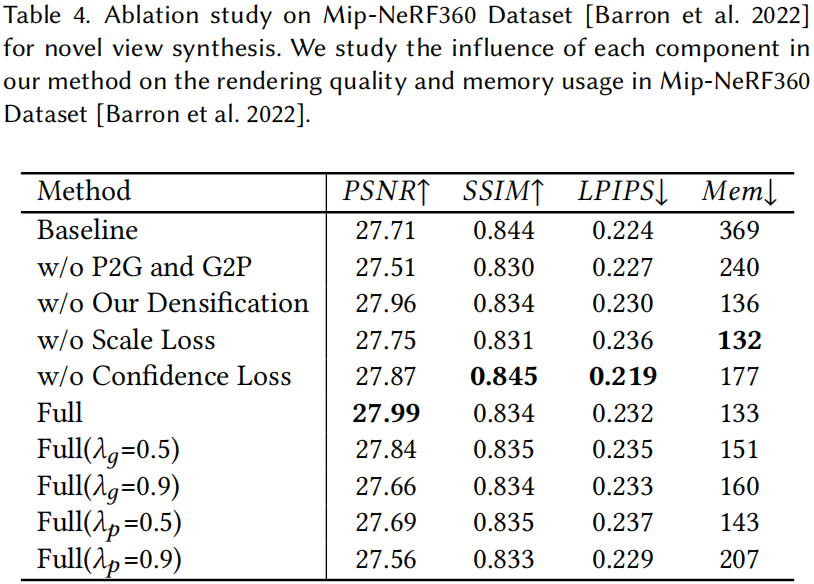
消融实验

拓展:公式8证明


#pic_center =80%x80%
d \sqrt{d} d 1 8 \frac {1}{8} 81 x ˉ \bar{x} xˉ D ^ \hat{D} D^ I ~ \tilde{I} I~ ϵ \epsilon ϵ
ϕ \phi ϕ ∏ \prod ∏ a b c \sqrt{abc} abc ∑ a b c \sum{abc} ∑abc
/ $$